A Digital Predistortion Technique Based on the Dimension Weighted Blind K-Nearest Neighbor Algorithm
-
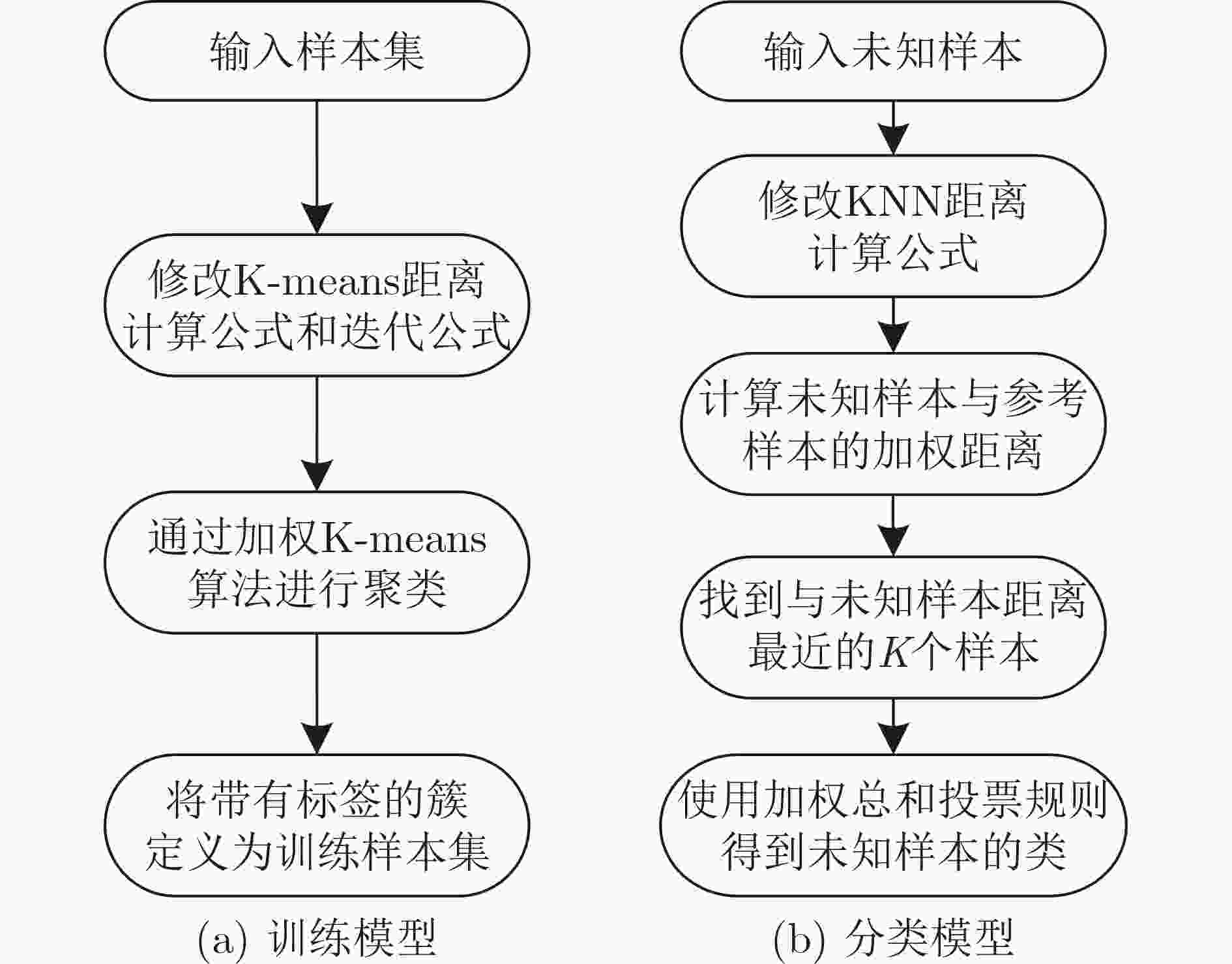
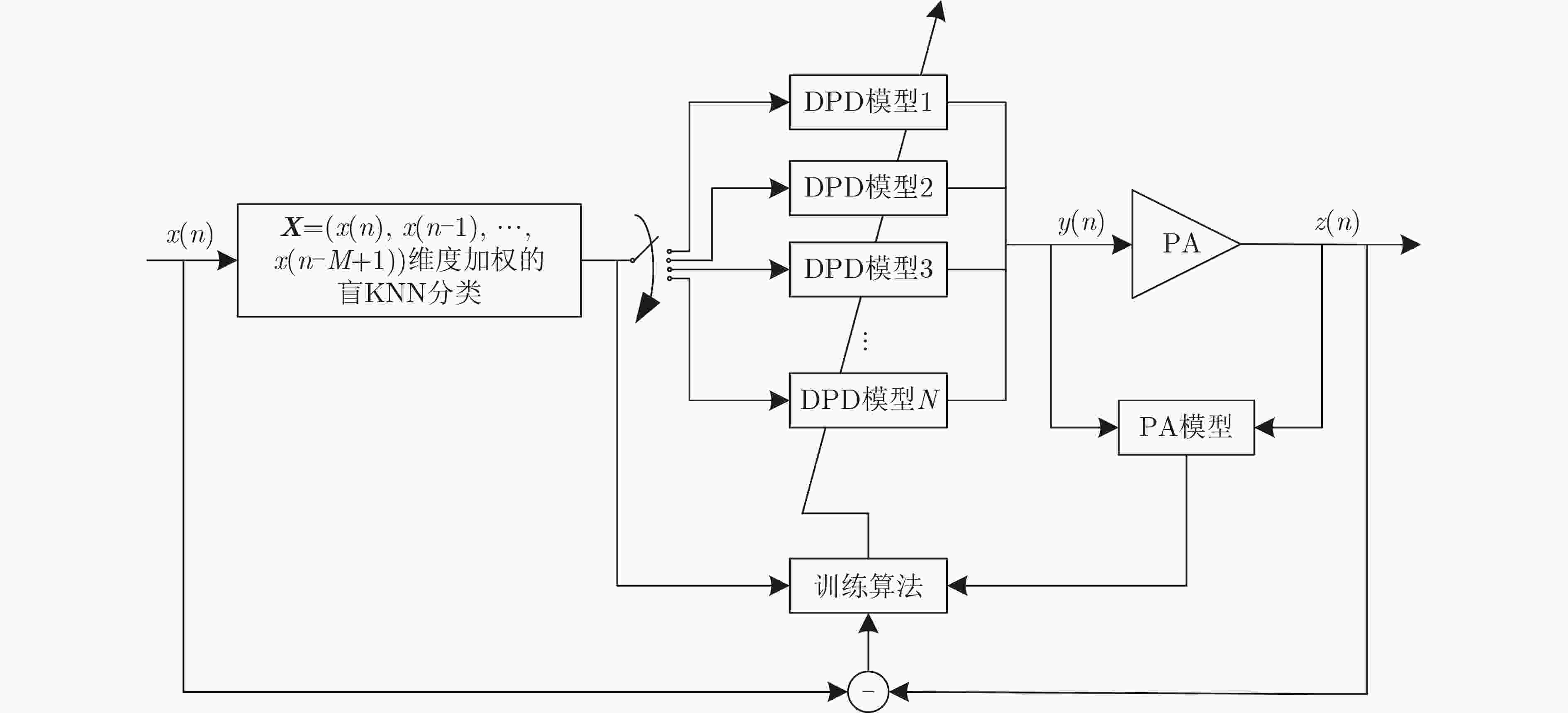
摘要: 传统的数字预失真(DPD)模型通常在所有的输入信号功率上采用单一多项式模型和单一记忆深度对功率放大器(PA)进行线性化矫正。然而,功率放大器在不同的功率水平下会呈现出不同的非线性特性,并产生不同的记忆效应。针对这一问题,该文提出一种基于维度加权盲K近邻(KNN)算法的数字预失真模型,所提模型根据功放当前输入信号以及记忆输入信号的幅度进行维度加权的KNN分类,组成维度加权盲KNN记忆多项式(WKMP)模型,并为每一类输入信号序列建立子模型。所提方法用Doherty功率放大器进行实验验证,使用带宽为30 MHz、频点为2.2 GHz的3载波长期演进(LTE)信号作为输入,反馈端使用122.88 MHz的采样率进行采样。实验结果表明,所提维度加权盲KNN分类方法与记忆多项式(MP)模型结合时,功放正向建模效果和数字预失真效果均超过了广义记忆多项式(GMP)模型,并远超记忆多项式模型的效果,实验结果验证了所提模型的优良性能。Abstract: In traditional Digital PreDistortion (DPD) models, the same set of polynomial models and the same memory model are usually used to linearize the Power Amplifier (PA) at all input signal powers. However, the PAs exhibit different nonlinear characteristics and different memory effects at different power levels. In order to solve this problem, a DPD model based on the blind K-Nearest Neighbor (KNN) algorithm with dimension weighting is proposed. The input signal sequence is classified by the proposed model according to the magnitudes of amplifier's current input signal and the memory input signal with the dimension-weighted KNN classification .And sub-models are established for each type of input signal sequence. The proposed method is verified experimentally by a Doherty PA, a three carrier Long Term Evolution (LTE) signal with a bandwidth of 30 MHz and a frequency point of 2.2 GHz is used as the input, the feedback channel is sampled using a sampling rate of 122.88 MHz. When the dimensional-weighted blind KNN classification method is combined with the Memory Polynomial (MP) model, the forward modeling performance and digital pre-distortion performance for the PA which exceed the performance of Generalized Memory Polynomial (GMP) model and MP model are manifested in the experiment. The excellent performance of the proposed model is verified in the experiment.
-
表 1 3种模型PA正向建模精度对比(dB)
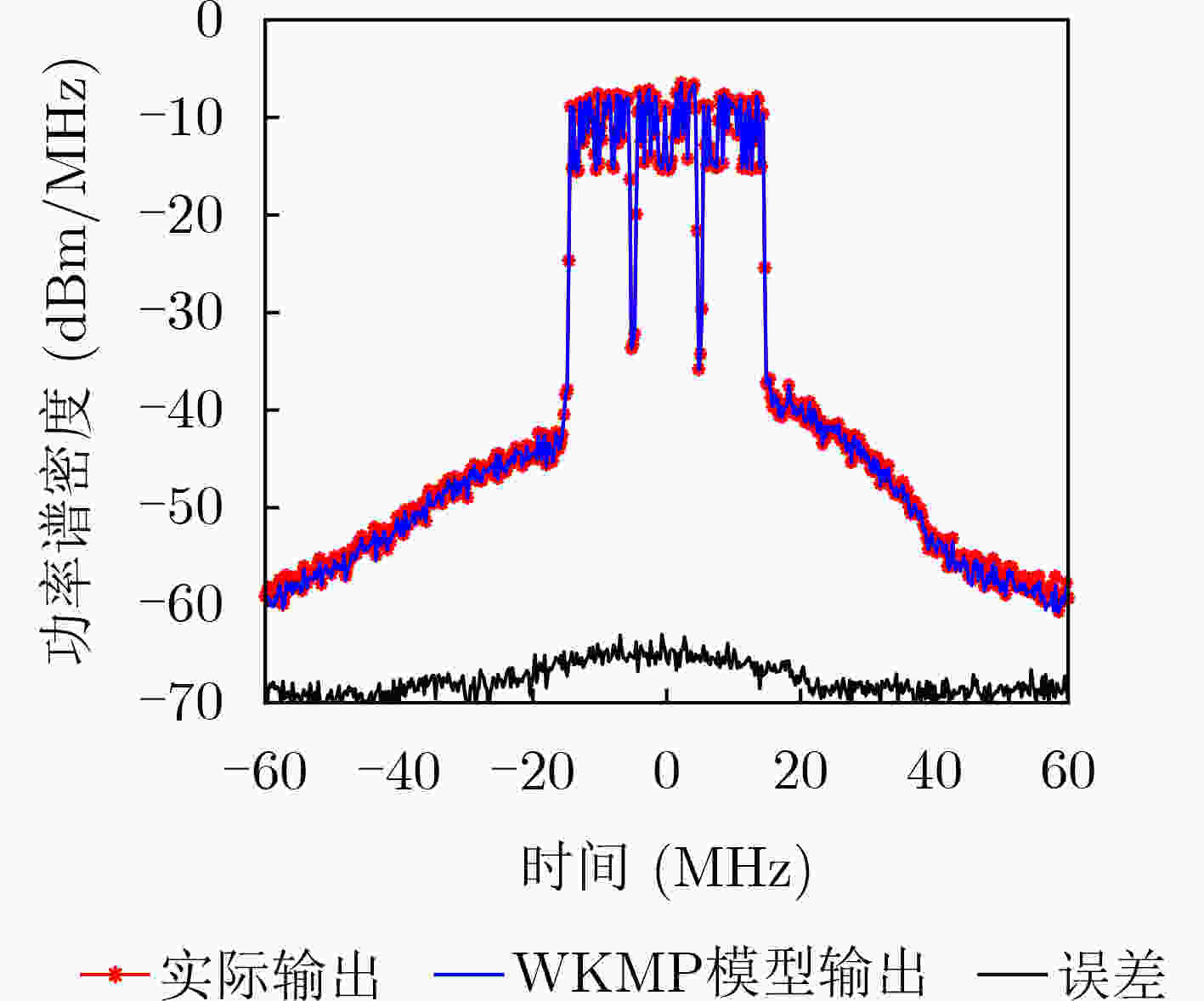
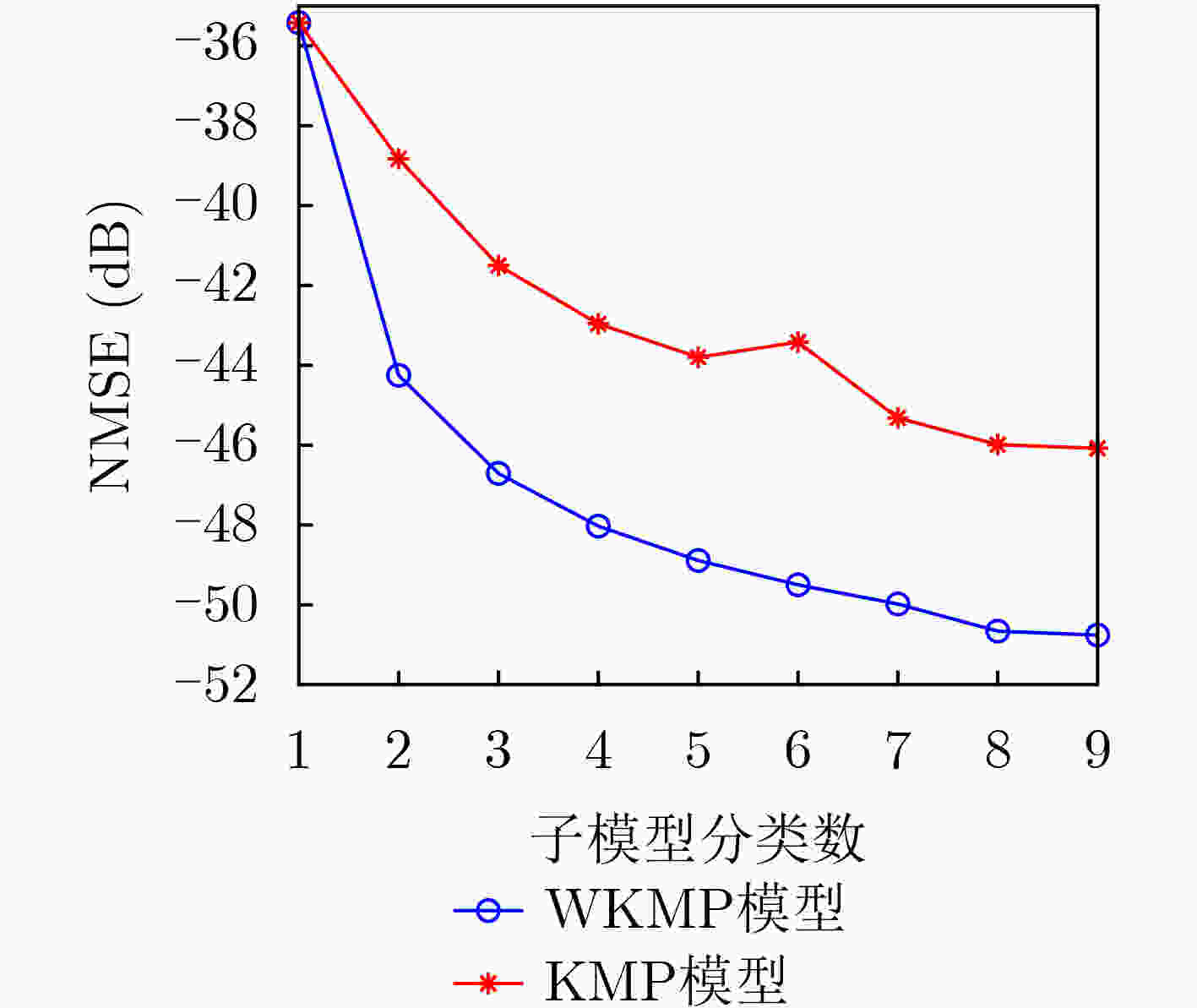
MP GMP KMP WKMP 建模精度NMSE –36.72 –47.99 –45.31 –50.67 表 2 各模型的DPD性能对比
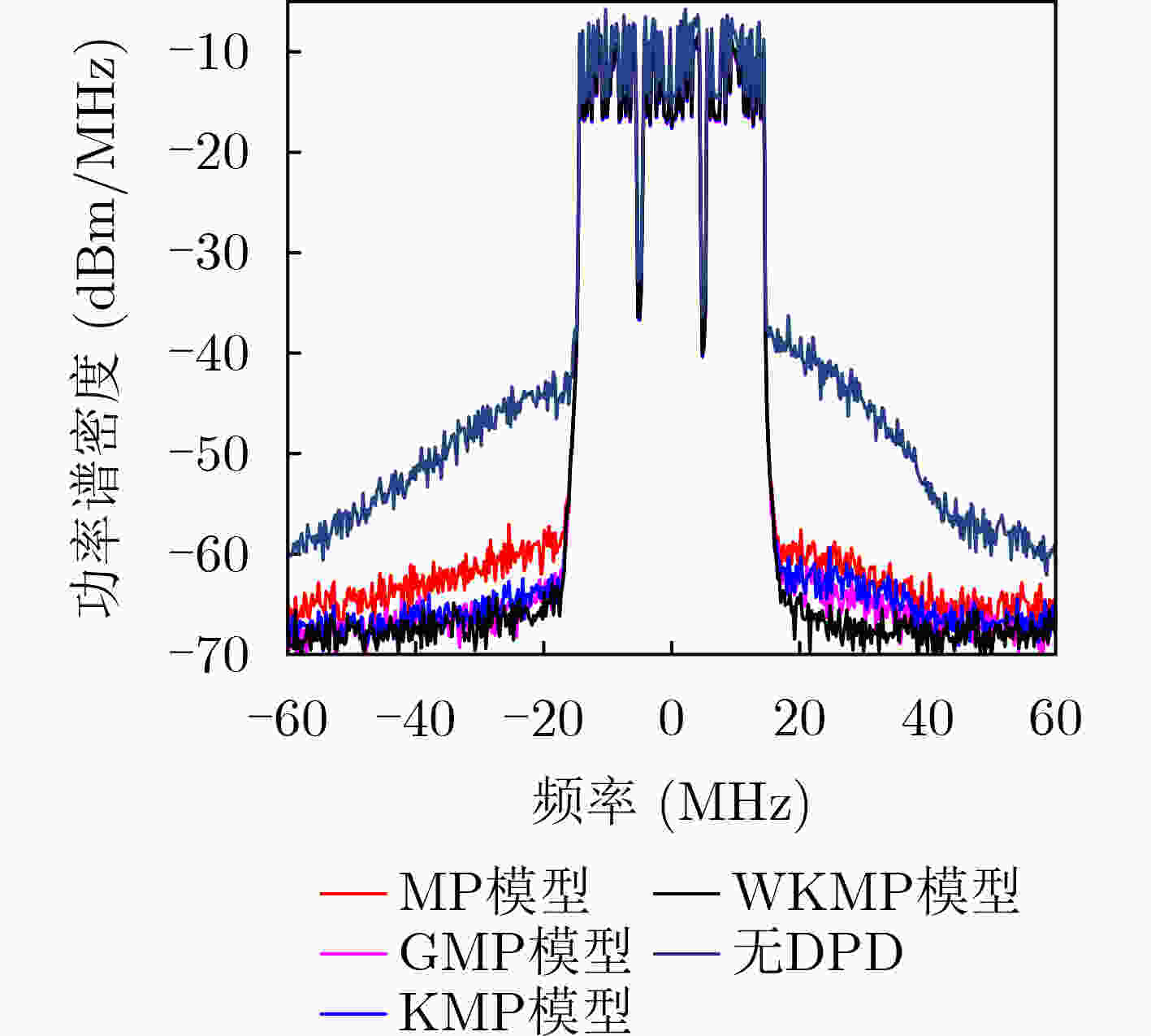
无预失真 记忆多项式 广义记忆多项式 K近邻记忆多项式 维度加权K近邻记忆多项式 线性化效果ACPR(dBc) –34.72/–33.00 –44.68/–45.16 –47.53/–46.96 –47.37/–46.36 –48.18/–48.34 还原效果NMSE(dB) –11.20 –31.47 –30.65 –34.76 –43.28 表 3 各模型的计算复杂度对比
预失真器 $ 1/D $ ${\boldsymbol{H\omega}}$ $({{\boldsymbol{H}}}^{ {\rm H} }{\boldsymbol{H}}{)}^{-1}{{\boldsymbol{H}}}^{{\rm{H}}}{\boldsymbol{e}}$ 总计算量 MP 0 ${ {{NP} }_{\rm{MP} } }$ $ NP_{\rm{MP}}^2 + P_{\rm{MP}}^3 + P_{\rm{MP}}^2 + N{P_{\rm{MP}}} $ 4460800 GMP 0 ${ {{NP} }_{ {\rm{GMP} } } }$ $NP_{{\rm{GMP}}}^2 + P_{{\rm{GMP}}}^3 + {P}_{ {{\rm{GMP}}} }^{2}{ + N}{ {P}_{ {{\rm{GMP}}} } }$ 140968656 KMP $ K(4N + N) $ ${ { {{NP} } }_{\rm{ {KMP} } } }$ $ \displaystyle\sum {{(NP}{{_{\rm{{KMP}}}^{2}}_i}{ + P}_{\rm{{KMP}}}^{3}{ + P}_{\rm{{KMP}}}^{2}{ + }{{N}_i}{{P}_{\rm{{KMP}}}}} {)} $ 45451264 WKMP $ K(4N + N) $ ${ {{NP} }_{\rm{WKMP} } }$ $ \displaystyle\sum {{(}{{N}_j}{P}_{{\rm{WKMP}}}^{2}{ + P}_{{\rm{WKMP}}}^{3}{ + P}_{{\rm{WKMP}}}^{2}{ + }{{N}_j}{{P}_{{\rm{WKMP}}}}} {)} $ 45451264 -
[1] SHAFI M, MOLISCH A F, SMITH P J, et al. 5G: A tutorial overview of standards, trials, challenges, deployment, and practice[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1201–1221. doi: 10.1109/JSAC.2017.2692307 [2] PHAM Q A, MONTORO G, LÓPEZ-BUENO D, et al. Dynamic selection and estimation of the digital predistorter parameters for power amplifier linearization[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(10): 3996–4004. doi: 10.1109/TMTT.2019.2923186 [3] GUAN Lei and ZHU Anding. Green communications: Digital predistortion for wideband RF power amplifiers[J]. IEEE Microwave Magazine, 2014, 15(7): 84–99. doi: 10.1109/MMM.2014.2356037 [4] WANG Siqi, HUSSEIN M A, VENARD O, et al. Optimal sizing of two-stage cascaded sparse memory polynomial model for high power amplifiers linearization[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(9): 3958–3965. doi: 10.1109/TMTT.2018.2838126 [5] LIU Youjiang, ZHOU Jie, CHEN Wenhua, et al. A robust augmented complexity-reduced generalized memory polynomial for wideband RF power amplifiers[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2389–2401. doi: 10.1109/TIE.2013.2270217 [6] LI Zhao, YU Cuiping, and LIU Yuan’an. A modified dynamic deviation reduction based Volterra model for digital predistortion of RF power amplifiers[C]. The 2019 IEEE 6th International Symposium on Electromagnetic Compatibility (ISEMC), Nanjing, China, 2019: 1–3. [7] 兰榕, 胡欣, 邹峰, 等. 基于循环平稳特性的欠采样宽带数字预失真研究[J]. 电子与信息学报, 2020, 42(5): 1274–1280. doi: 10.11999/JEIT190105LAN Rong, HU Xin, ZOU Feng, et al. Research of low sampling frequency broadband digital predistortion with cyclostationary characteristics[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1274–1280. doi: 10.11999/JEIT190105 [8] 蔡天赋, 李明玉, 靳一, 等. 基于Landweber迭代算法的欠采样恢复数字预失真技术[J]. 电子与信息学报, 2021, 43(11): 3166–3173. doi: 10.11999/JEIT201051CAI Tianfu, LI Mingyu, JIN Yi, et al. An under-sampling restoration digital predistortion technique based on Landweber iteration algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(11): 3166–3173. doi: 10.11999/JEIT201051 [9] ZHU Anding, DRAXLER P J, HSIA C, et al. Digital predistortion for envelope-tracking power amplifiers using decomposed piecewise Volterra series[J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(10): 2237–2247. doi: 10.1109/TMTT.2008.2003529 [10] GHARAIBEH K M. Behavioral modeling of nonlinear power amplifiers using threshold decomposition-based piece wise linear approximation[C]. 2008 IEEE Radio and Wireless Symposium, Orlando, USA, 2008: 755–758. [11] YOUNES M, KWAN A, AKBARPOUR M, et al. Two-dimensional piecewise behavioral model for highly nonlinear dual-band transmitters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8666–8675. doi: 10.1109/TIE.2017.2703683 [12] AFSARDOOST S, ERIKSSON T, and FAGER C. Digital predistortion using a vector-switched model[J]. IEEE Transactions on Microwave Theory and Techniques, 2012, 60(4): 1166–1174. doi: 10.1109/TMTT.2012.2184295 [13] LI Yue, CAO Wenhui, and ZHU Anding. Instantaneous sample indexed magnitude-selective affine function-based behavioral model for digital predistortion of RF power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(11): 5000–5010. doi: 10.1109/TMTT.2018.2855134 [14] LI Yue, WANG Xiaoyu, PANG Jingzhou, et al. Boosted model tree-based behavioral modeling for digital predistortion of RF power amplifiers[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(9): 3976–3988. doi: 10.1109/TMTT.2021.3081096 [15] ZHANG Junfeng, GAO Mingyi, CHEN Wei, et al. Non-data-aided k-nearest neighbors technique for optical fiber nonlinearity mitigation[J]. Journal of Lightwave Technology, 2018, 36(17): 3564–3572. doi: 10.1109/JLT.2018.2837689 [16] HUANG Xiaohui, YANG Xiaofei, ZHAO Junhui, et al. A new weighting k-means type clustering framework with an l2-norm regularization[J]. Knowledge-Based Systems, 2018, 151: 165–179. doi: 10.1016/J.KNOSYS.2018.03.028 [17] DING Lei, MUJICA F, and YANG Zigang. Digital predistortion using direct learning with reduced bandwidth feedback[C]. 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, USA, 2013: 1–3. -





 下载:
下载:



 下载:
下载:
