Specific Emitter Identification Based on Regression Analysis Theory
-
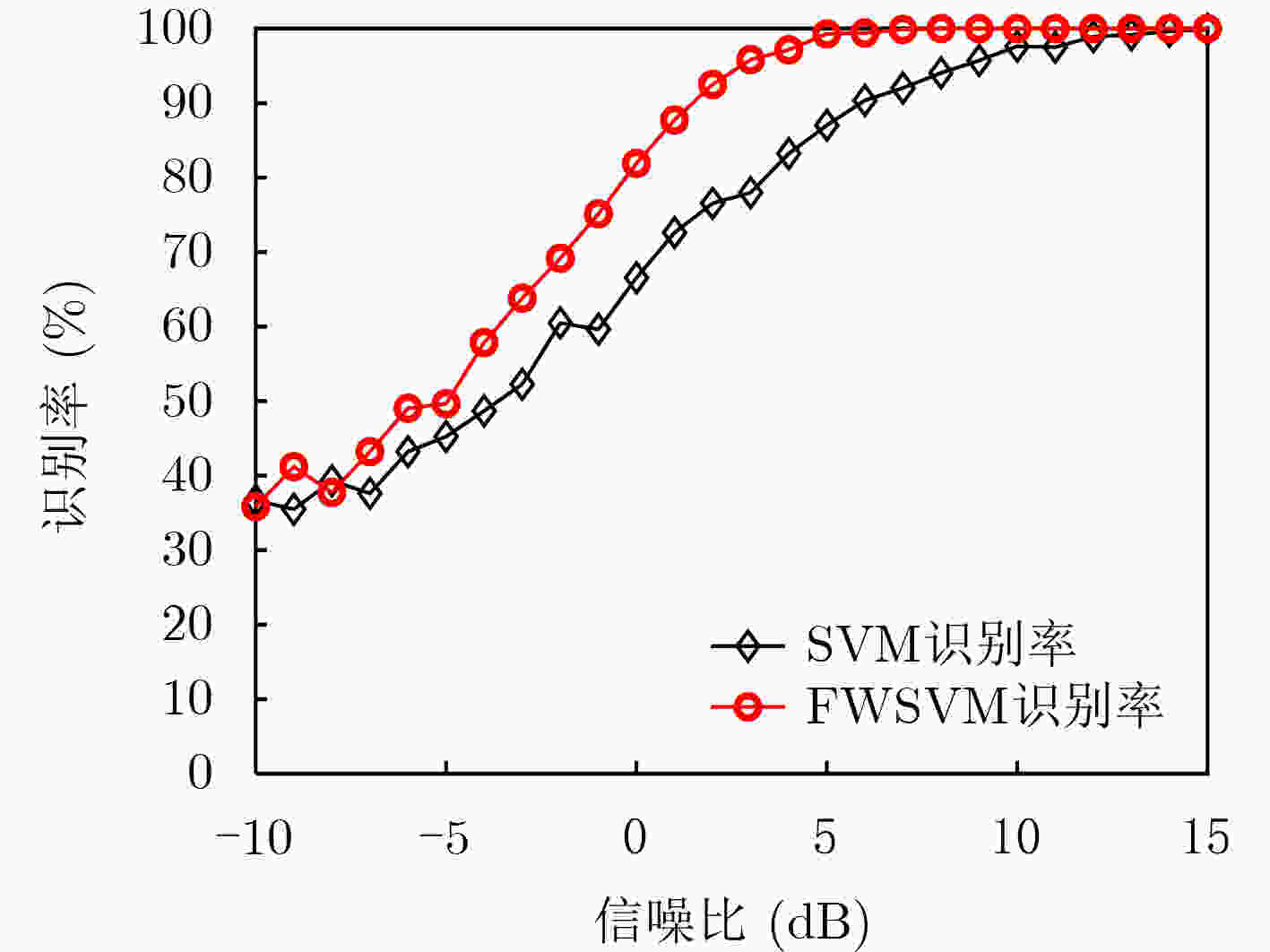
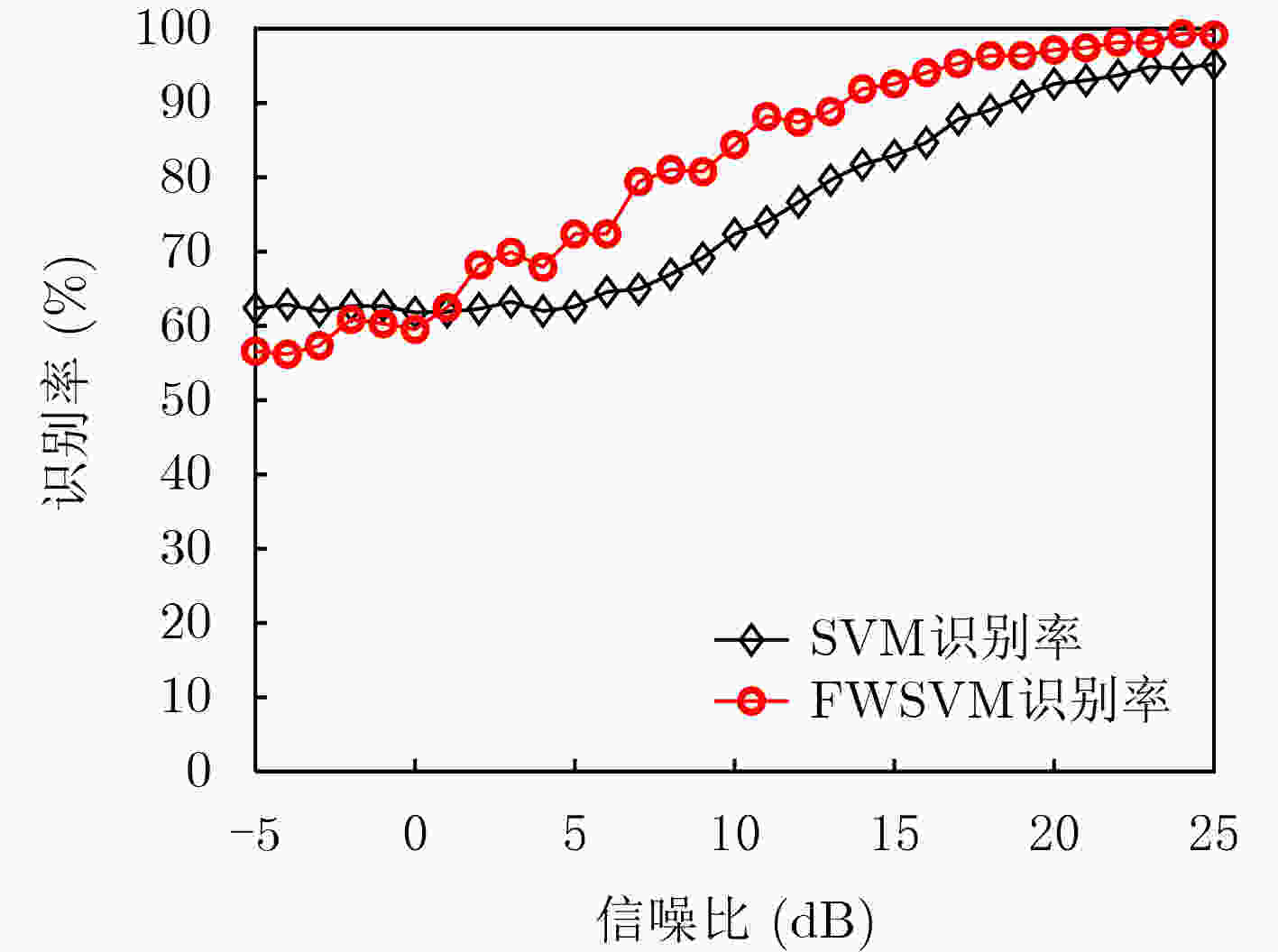
摘要: 针对目前辐射源个体识别未能将信号特征与硬件组成相联系的问题，该文使用高阶谱分析和变分模态分解(VMD)两种特征提取手段，进行研究分析，采用围线双谱积分以及改进变分模态分解技术对半实物平台仿真信号以及软件仿真(ADS)输出信号进行特征提取并分析。通过软件仿真定量分析辐射源相位噪声以及功率放大电路非线性失真对信号无意调制特征的影响，对变量进行相关性分析，并对其中显著相关的变量进行回归拟合，得到其相关回归函数。然后利用硬件与特征的相关性，改进传统支持向量机(SVM)分类器，构建相关性权重支持向量机分类器。最后分别以软件仿真输出信号以及半实物仿真平台实测信号为样本进行验证，结果表明，同信噪比下权重支持向量机与传统支持向量机相比分类准确率提升在10%以上。Abstract: Focusing on the problem that the signal characteristics are not related to the hardware composition in the specific emitter identification, two feature extraction methods are used in this paper: high-order spectral analysis and Variational Modal Decomposition (VMD) for research and analysis. The surrounding-line bispectral integration and improved VMD technology are used to extract and analyze the features of the hardware in the semi-physical simulation signal and Advanced Design System (ADS) output signal. Through ADS, the influence of emitter phase noise and nonlinear distortion of power amplifier on signal unintentional modulation characteristics is quantitatively analyzed, the correlation of variables is analyzed, and the significantly related variables are regressed and fitted to obtain their correlation regression function. Using the correlation between hardware and features, the traditional Support Vector Machines (SVM) classifier is improved to construct a correlation weight SVM classifier. Finally, the results show that the classification accuracy of weighted SVM is improved by more than 10% compared with single core SVM under the same signal-to-noise ratio.
-
表 2 无意调制特征正态性检验
特征 柯尔莫戈洛夫-斯米诺夫(V)a 夏皮洛-威尔克 统计 自由度 显著性 统计 自由度 显著性 波形熵 0.114 40 0.200* 0.926 40 0.012 能量熵 0.084 40 0.200* 0.985 40 0.046 均值 0.173 40 0.004 0.869 40 0.000 VMD能量熵 0.237 40 0.000 0.857 40 0.000 VMD均值 0.098 40 0.200* 0.955 40 0.016 VMD分类系数 0.121 40 0.142 0.941 40 0.036 a-里利氏显著性修正
*-显著性下限
下载: 导出CSV
表 3 振荡器相位噪声强度与特征相关性
双谱均值 双谱波形熵 双谱能量熵 VMD能量熵 VMD均值 VMD分类系数 相位噪声强度 相关系数 –0.064 0.188 0.542 0.244 0.116 0.029 显著性 0.697 0.245 0.000 0.129 0.478 0.857
下载: 导出CSV
表 4 回归系数表
未标准化系数 标准化系数β t 显著性 B 标准错误 (常量) 12.426 0.009 – 1461.697 0.000 相位噪声强度 0.003 0.001 0.542 3.979 0.000
下载: 导出CSV
表 6 不同偏置电压PA输出信号无意调制特征正态性检验
特征 柯尔莫戈洛夫-斯米诺夫(V)a 夏皮洛-威尔克(S-W) 统计 自由度 显著性 统计 自由度 显著性 波形熵 0.182 40 0.002 0.885 40 0.001 能量熵 0.126 40 0.112 0.935 40 0.024 均值 0.178 40 0.003 0.850 40 0.000 VMD能量熵 0.207 40 0.000 0.850 40 0.000 均值 0.167 40 0.007 0.926 40 0.012 分类系数 0.224 40 0.000 0.792 40 0.000
下载: 导出CSV
表 7 PA偏置电压与无意调制特征相关性系数
检验类型 双谱波形熵 双谱能量熵 双谱均值 VMD能量熵 VMD均值 分类系数 相关系数 –0.565 –0.755 –0.911 –0.855 –0.267 0.766 显著性 0.000 0.000 0.000 0.000 0.095 0.000
下载: 导出CSV
表 8 PA偏置电压与双谱均值回归方程系数
未标准化系数 标准化系数β t 显著性 B 标准错误 (常量) 5 568.890 321.304 – 17.332 0.000 偏置电压系数 –156.125 11.486 –0.911 13.593 0.000
下载: 导出CSV
表 9 回归方程F统计量检验
模型 平方和 自由度 均方 F 显著性 回归 1 299 186.476 1 1 299 186.476 184.763 0.000 残差 267 201.518 38 7 031.619 – – 总计 1 566 387.993 39 – – –
下载: 导出CSV
表 11 各特征变量回归模型
自变量 无意调制特征 回归方程 拟合优度 PA偏置电压 VMD能量熵 y=–0.18x+0.534 0.752 VMD分类系数 y=–0.001 83x–0.005 0.576 双谱能量熵 y=–0.41x+13.515 0.559 双频谱均值 y=–0.383x+6.164 0.302
下载: 导出CSV
表 13 半实物仿真平台配置及参数设置
辐射源
个体功率放
大器老化
时长(h)芯片型号 2.4GHz增益(dB) E1 PA1 0 SBB5089ZP48G 16.85 E2 PA2 168 SBB5089ZP5NH 16.92 E3 PA3 336 SBB5089ZP2VR 16.81 E4 PA4 504 SBB5089ZP2MX 16.76
下载: 导出CSV
-
[1] DONG Zeyu, LV Fengrong, WAN Tao, et al. Radar signal modulation recognition based on bispectrum features and deep learning[C]. 2021 International Conference on Computer Engineering and Application (ICCEA), Kunming, China, 2021: 63–67. [2] 关键, 伍僖杰, 丁昊, 等. 基于对角积分双谱的海面慢速小目标检测方法[J]. 电子与信息学报, 2022, 44(7): 2449–2460. doi: 10.11999/JEIT210408GUAN Jian, WU Xijie, DING Hao, et al. A method for detecting small slow targets in sea surface based on diagonal integrated bispectrum[J]. Journal of Electronics &Information Technology, 2022, 44(7): 2449–2460. doi: 10.11999/JEIT210408 [3] LIN Yun, JIA Jicheng, WANG Sen, et al. Wireless device identification based on radio frequency fingerprint features[C]. 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 2020: 1–6. [4] DRAGOMIRETSKIY K and ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531–544. doi: 10.1109/TSP.2013.2288675 [5] 李晟, 徐飞洋, 李玉晓, 等. 基于变分模式分解和门循环单元的电子系统间歇故障严重程度评估方法[J]. 电子与信息学报, 2022, 44(10): 3673–3682. doi: 10.11999/JEIT210795LI Sheng, XU Feiyang, LI Yuxiao, et al. A method for evaluating the severity of intermittent faults of electronic systems based on VMD-GRU[J]. Journal of Electronics &Information Technology, 2022, 44(10): 3673–3682. doi: 10.11999/JEIT210795 [6] GOK G, ALP Y K, and ARIKAN O. A new method for specific emitter identification with results on real radar measurements[J]. IEEE Transactions on Information Forensics and Security, 2020, 15: 3335–3346. doi: 10.1109/TIFS.2020.2988558 [7] GOK G, ALP Y K, and ALTIPARMAK F. Radar fingerprint extraction via variational mode decomposition[C]. The 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 2017: 1–4. [8] CHEN Shiqian, DONG Xingjian, PENG Zhike, et al. Nonlinear chirp mode decomposition: A variational method[J]. IEEE Transactions on Signal Processing, 2017, 65(22): 6024–6037. doi: 10.1109/TSP.2017.2731300 [9] LIU Mingwei and DOHERTY J F. Specific emitter identification using nonlinear device estimation[C]. 2008 IEEE Sarnoff Symposium, Princeton, USA, 2008: 1–5. [10] POLAK A C and GOECKEL D L. Wireless device identification based on RF oscillator imperfections[C]. 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 2014: 2679–2683. [11] RISQIWATI D, WIBAWA A D, PANE E S, et al. Feature selection for EEG-based fatigue analysis using pearson correlation[C]. 2020 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 2020: 164–169. [12] 董小伟, 韩悦, 张正, 等. 基于多尺度加权特征融合网络的地铁行人目标检测算法[J]. 电子与信息学报, 2021, 43(7): 2113–2120. doi: 10.11999/JEIT200450DONG Xiaowei, HAN Yue, ZHANG Zheng, et al. Metro pedestrian detection algorithm based on multi-scale weighted feature fusion network[J]. Journal of Electronics &Information Technology, 2021, 43(7): 2113–2120. doi: 10.11999/JEIT200450 [13] HUANG Jing, ZHOU Jinzhi, and ZHENG Linwen. Support vector machine classification algorithm based on relief-F feature weighting[C]. 2020 International Conference on Computer Engineering and Application (ICCEA), Guangzhou, China, 2020: 547–553. [14] 陈韬伟, 金炜东, 李杰. 基于围线积分双谱的雷达辐射源信号个体特征提取[J]. 计算机工程与应用, 2013, 49(8): 209–212,252. doi: 10.3778/j.issn.1002-8331.1109-0034CHEN Taowei, JIN Weidong, and LI Jie. Individual feature extraction from radar emitter signals based on surrounding-line integral bispectrum[J]. Computer Engineering and Applications, 2013, 49(8): 209–212,252. doi: 10.3778/j.issn.1002-8331.1109-0034 [15] 罗亦泳, 姚宜斌, 黄城, 等. 基于改进VMD的变形特征提取与分析[J]. 武汉大学学报:信息科学版, 2020, 45(4): 612–619. doi: 10.13203/j.whugis20180286LUO Yiyong, YAO Yibin, HUANG Cheng, et al. Deformation feature extraction and analysis based on improved variational mode decomposition[J]. Geomatics and Information Science of Wuhan University, 2020, 45(4): 612–619. doi: 10.13203/j.whugis20180286 -
图(5) / 表(13)
计量
- 文章访问数: 534
- HTML全文浏览量: 312
- PDF下载量: 139
- 被引次数: 0
下载:
