Blockchain Security Situational Awareness Method Based on Markov Attack Graph and Game Model
-
摘要: 全面准确地感知区块链网络中各节点所遭受的日蚀攻击情况是一个难题,该文针对该难题提出一种基于Markov攻击图和博弈模型的区块链安全态势感知方法。该方法结合区块链网络各节点以及日蚀攻击的特点建立Markov攻击图模型,随后将该模型进行量化从而计算各攻击路径的转换概率,选择较高概率的攻击路径进行多阶段攻防博弈并计算双方的最大目标函数值。通过分析这些函数值,完成对整个区块链网络节点的安全态势感知,达到对未来安全情况的预测和系统维护的目的。实验对比表明,该模型方法不但具有较低的入侵成功次数,还具有较好的确保系统完整性等方面的优势。Abstract: It is a difficult problem to perceive comprehensively and accurately the eclipse attack of each node in the blockchain network. For this problem, this paper proposes a blockchain security situational awareness method based on the Markov attack graph and game model. The method combines the characteristics of each node of the blockchain network and the eclipse attack to establish a Markov attack graph model, then quantifies the model to calculate the conversion probability of each attack path, and selects the attack path with higher probability to conduct a multi-stage attack and defense game and calculates the maximum objective function value of both sides. By analyzing these function values, the security situation awareness of the entire blockchain network node is completed, and the purpose of predicting the future security situation and system maintenance is achieved. The experimental comparison shows that the model method not only has a low number of successful intrusions but also has the advantage of ensuring the integrity of the system.
-
Key words:
- Markov attack graph /
- Game theory /
- Blockchain /
- Eclipse attack /
- Security situation
-
表 1 区块链网络安全状态
安全状态 状态描述 安全状态 状态描述 安全状态 状态描述 $ Z_0^1 $ 区块链节点正常状态 $ Z_0^2 $ 攻击者获取受害节点的ID $ Z_0^3 $ 攻击者持续向受害节点
发送Ping消息$ Z_0^4 $ 受害者回复Pong消息
并记录在tried表中$ Z_0^5 $ 攻击者持续向受害者发送ADDR消息 $ Z_0^6 $ 受害者回复Pong消息并记录在new表中 $ Z_0^7 $ 受害节点重启 $ Z_0^8 $ 攻击者持续向受害者发送Ping消息和ADDR消息 $ Z_0^9 $ 攻击者占据受害者的tried表和new表 表 2 状态转变概率表
状态转移 转移概率 状态转移 转移概率 状态转移 转移概率 状态转移 转移概率 $ {Z_1} \to Z_0^2 $ P12=0.9 $ {Z_3} \to Z_0^5 $ P35=0.5 $ {Z_5} \to Z_0^6 $ P56=0.4 $ {Z_7} \to Z_0^8 $ P78=0.7 $ {Z_2} \to Z_0^3 $ P23=0.3 $ {Z_4} \to Z_0^5 $ P45=0.4 $ {Z_5} \to Z_0^7 $ P57=0.3 $ {Z_7} \to Z_0^9 $ P79=0.3 $ {Z_2} \to Z_0^4 $ P24=0.3 $ {Z_4} \to Z_0^6 $ P46=0.3 $ {Z_5} \to Z_0^8 $ P58=0.3 $ {Z_8} \to Z_0^9 $ P89=0.4 $ {Z_2} \to Z_0^5 $ P25=0.4 $ {Z_4} \to Z_0^7 $ P47=0.1 $ {Z_6} \to Z_0^7 $ P67=0.4 $ {Z_3} \to Z_0^4 $ P34=0.5 $ {Z_4} \to Z_0^8 $ P48=0.2 $ {Z_6} \to Z_0^8 $ P68=0.6 表 3 攻击路径
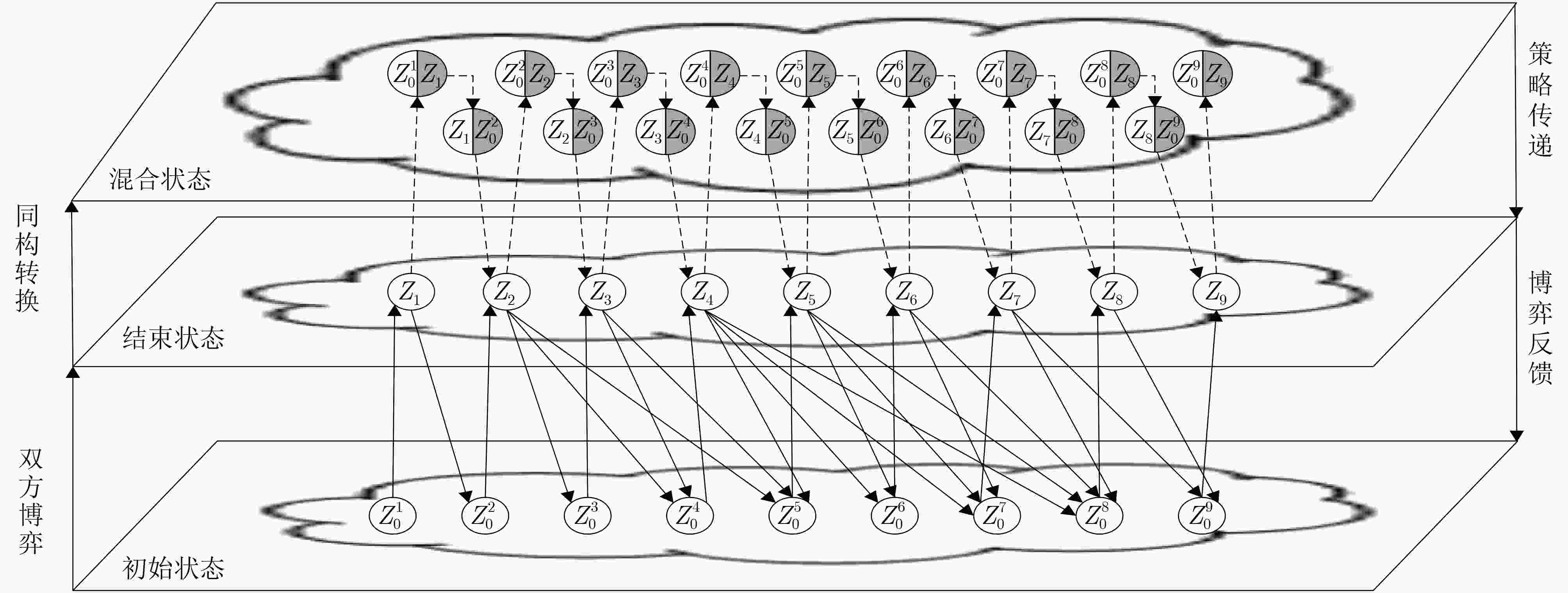
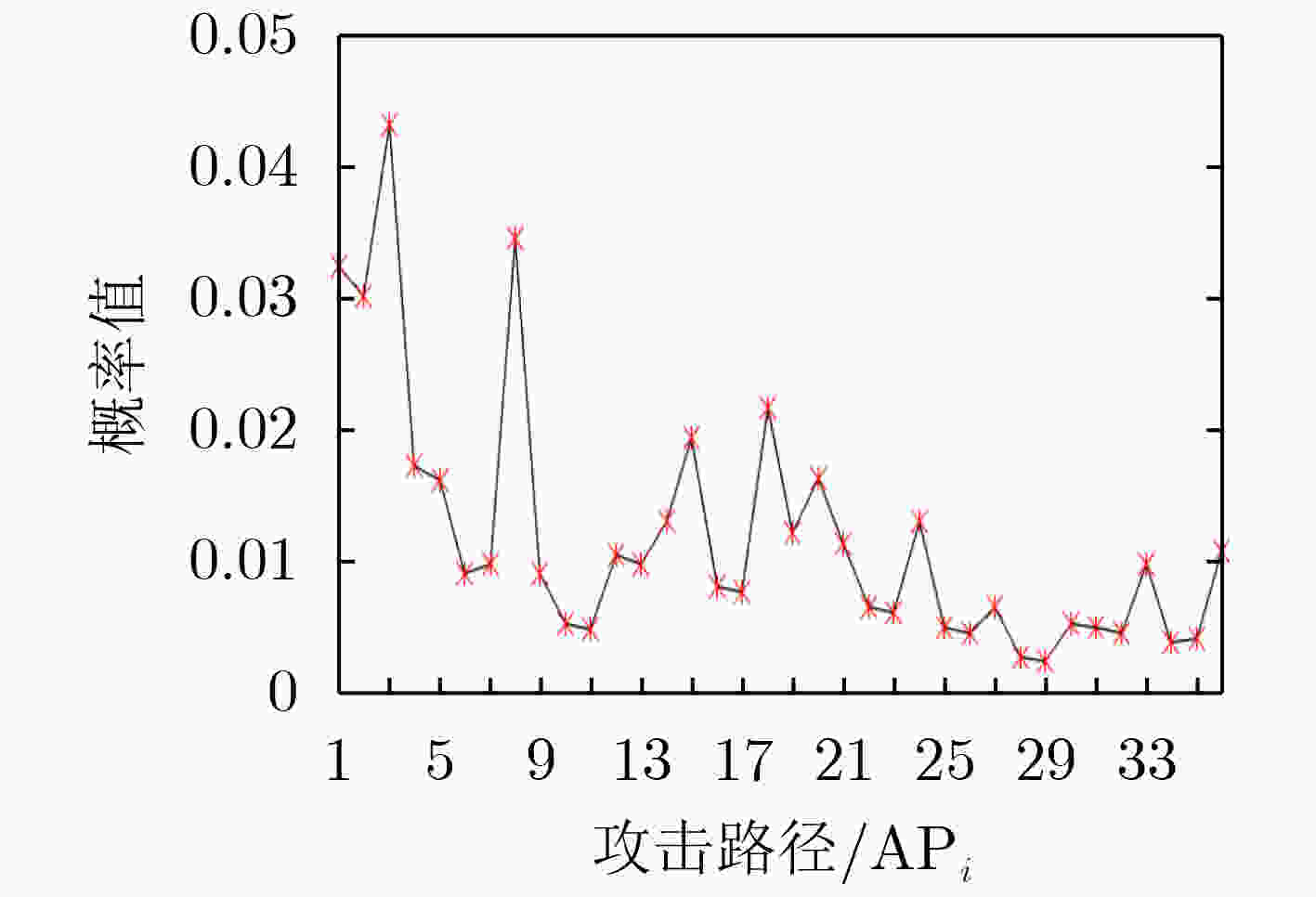
编号 攻击路径 编号 攻击路径 AP1 $ Z_0^1 $→Z1→$Z_0^2$→Z2→$Z_0^5$→Z5→$Z_0^7$→Z7→$Z_0^9$→Z9 AP2 $Z_0^1$→Z1→$Z_0^2$→Z2→$Z_0^5$→Z5→$Z_0^7$→Z7→$Z_0^8$→Z8→$Z_0^9$→Z9 AP3 $Z_0^1$→Z1→$Z_0^2$→Z2→$Z_0^5$→Z5→$Z_0^8$→Z8→$Z_0^9$→Z9 AP4 $Z_0^1$→Z1→$Z_0^2$→Z2→$Z_0^5$→Z5→$Z_0^6$→Z6→$Z_0^7$→Z7→$Z_0^9$→Z9 $\vdots $ $\vdots $ $\vdots $ $\vdots $ AP35 $Z_0^1$→Z1→$Z_0^2$→Z2→$Z_0^3$→Z3→$Z_0^4$→Z4→$Z_0^7$→Z7→$Z_0^9$→Z9 AP36 $Z_0^1$→Z1→$Z_0^2$→Z2→$Z_0^3$→Z3→$Z_0^4$→Z4→$Z_0^8$→Z8→$Z_0^9$→Z9 -
[1] 魏松杰, 吕伟龙, 李莎莎. 区块链公链应用的典型安全问题综述[J]. 软件学报, 2022, 33(1): 324–355. doi: 10.13328/j.cnki.jos.006280WEI Songjie, LV Weilong, and LI Shasha. Overview on typical security problems in public blockchain applications[J]. Journal of Software, 2022, 33(1): 324–355. doi: 10.13328/j.cnki.jos.006280 [2] WU Di, LIU Xiangdong, YAN Xiangbin, et al. Equilibrium analysis of bitcoin block withholding attack: A generalized model[J]. Reliability Engineering & System Safety, 2019, 185(10): 318–328. doi: 10.1016/j.ress.2018.12.026 [3] 胡浩, 叶润国, 张红旗, 等. 基于攻击预测的网络安全态势量化方法[J]. 通信学报, 2017, 38(10): 122–134. doi: 10.11959/j.issn.1000-436x.2017204HU Hao, YE Runguo, ZHANG Hongqi, et al. Quantitative method for network security situation based on attack prediction[J]. Journal on Communications, 2017, 38(10): 122–134. doi: 10.11959/j.issn.1000-436x.2017204 [4] LIU Xiaojun, WANG Wenbo, NIYATO D, et al. Evolutionary game for mining pool selection in blockchain networks[J]. IEEE Wireless Communications Letters, 2018, 7(5): 760–763. doi: 10.1109/LWC.2018.2820009 [5] 叶聪聪, 李国强, 蔡鸿明, 等. 区块链的安全检测模型[J]. 软件学报, 2018, 29(5): 1348–1359. doi: 10.13328/j.cnki.jos.005500YE Congcong, LI Guoqiang, CAI Hongming, et al. Security detection model of blockchain[J]. Journal of Software, 2018, 29(5): 1348–1359. doi: 10.13328/j.cnki.jos.005500 [6] KIM S K. Blockchain governance game[J]. Computers & Industrial Engineering, 2019, 136: 373–380. doi: 10.1016/j.cie.2019.07.004 [7] ZHAO Ning, WU Hao, and CHEN Yali. Coalition game-based computation resource allocation for wireless blockchain networks[J]. IEEE Internet of Things Journal, 2019, 6(5): 8507–8518. doi: 10.1109/JIOT.2019.2919781 [8] DU Xiaoli, LI Dengfeng, and LIANG Kairong. A biform game approach to preventing block withholding attack of blockchain based on semi-CIS value[J]. International Journal of Computational Intelligence Systems, 2019, 12(2): 1353–1360. doi: 10.2991/ijcis.d.191030.001 [9] 王雷, 任南, 李保珍. 区块链51%双花攻击的进化博弈及防控策略研究[J]. 计算机工程与应用, 2020, 56(3): 28–34. doi: 10.3778/j.issn.1002-8331.1907-0344WANG Lei, REN Nan, and LI Baozhen. Research on evolutionary game and prevention and control strategy of blockchain 51% double spend attack[J]. Computer Engineering and Applications, 2020, 56(3): 28–34. doi: 10.3778/j.issn.1002-8331.1907-0344 [10] ALANGOT B, REIJSBERGEN D, VENUGOPALAN S, et al. Decentralized and lightweight approach to detect eclipse attacks on proof of work blockchains[J]. IEEE Transactions on Network and Service Management, 2021, 18(2): 1659–1672. doi: 10.1109/TNSM.2021.3069502 [11] TAN Qingfeng, GAO Yue, SHI Jinqiao, et al. Toward a comprehensive insight into the eclipse attacks of tor hidden services[J]. IEEE Internet of Things Journal, 2019, 6(2): 1584–1593. doi: 10.1109/JIOT.2018.2846624 [12] 罗智勇, 杨旭, 刘嘉辉, 等. 基于贝叶斯攻击图的网络入侵意图分析模型[J]. 通信学报, 2020, 41(9): 160–169. doi: 10.11959/j.issn.1000-436x.2020172LUO Zhiyong, YANG Xu, LIU Jiahui, et al. Network intrusion intention analysis model based on Bayesian attack graph[J]. Journal on Communications, 2020, 41(9): 160–169. doi: 10.11959/j.issn.1000-436x.2020172 -





 下载:
下载:


 下载:
下载:
