Expanded Capacity Orthogonal Noise Suppression Multi-level Differential Chaotic Shift Keying Communication System
-
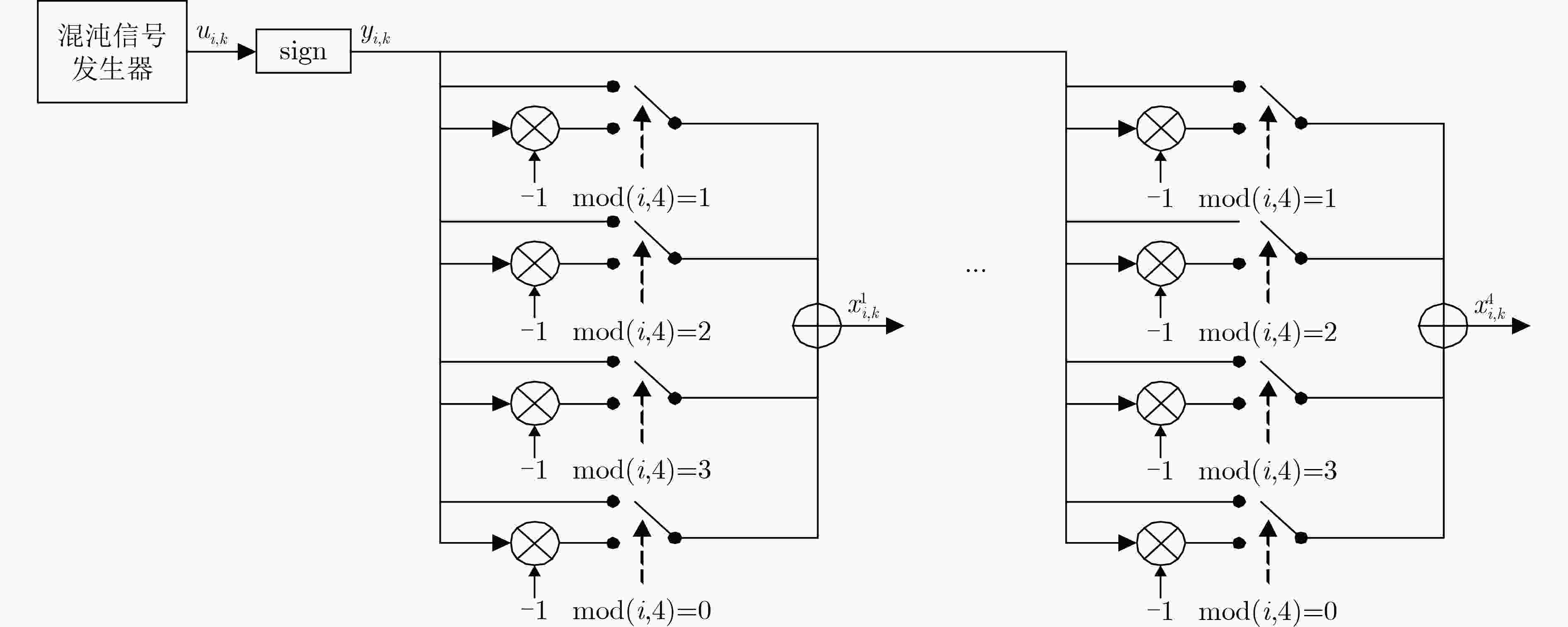
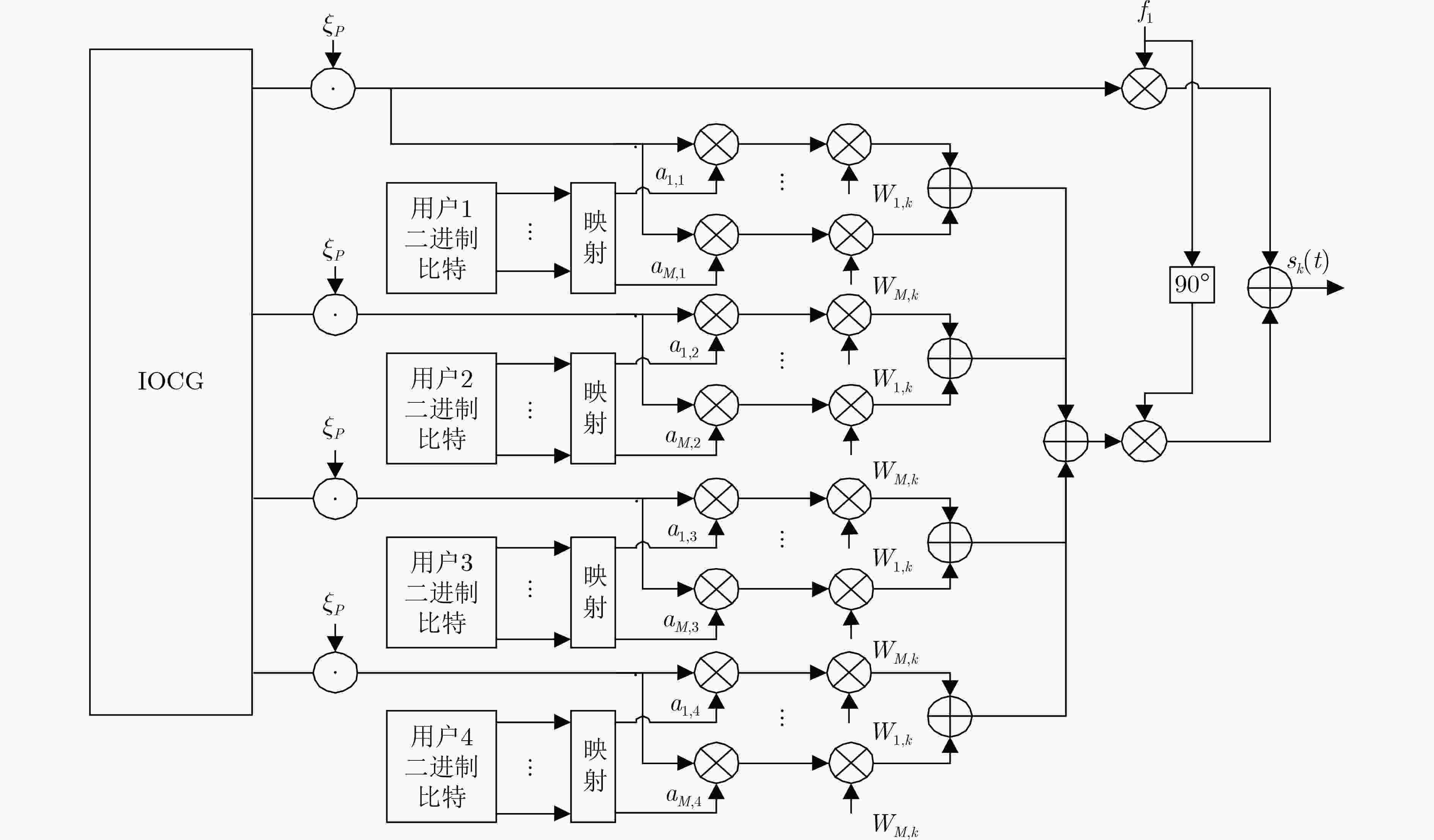
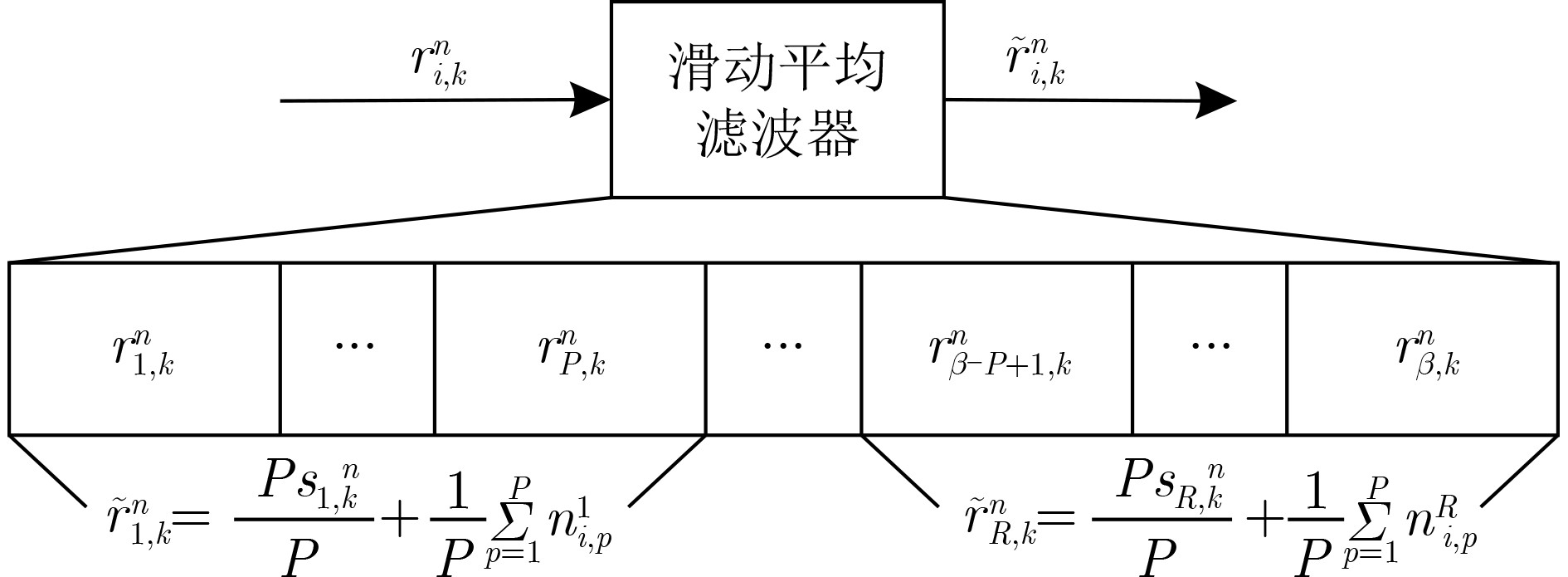
摘要: 针对多进制差分混沌移位键控系统传输速率较小且误码率(BER)较差的缺点,该文提出一种扩容型正交抑噪多进差分混沌移位键控(DCSK)通信系统。在该系统的发送端设计了一种改进型混沌基信号发生器,可产生4组正交的混沌基信号,使得通信容量极大提升。定义综合效用函数,并引入粒子群算法对系统各参数优化。对该系统在加性高斯白噪声(AWGN)和Rayleigh衰落信道下理论误码率公式进行推导及系统仿真同时对比不同系统的综合效用函数。结果表明,该系统具有更低的误码率和更优综合效用,具有较好的实际应用价值。Abstract: To address the disadvantages of small transmission rate and poor Bit Error Rate (BER) of M-ary differential chaos shift keying. An expanded capacity orthogonal noise suppression multi-level Differential Chaotic Shift Keying (DCSK) communication system is proposed. An improved orthogonal chaotic signal generator is designed at the transmitter of the system. It can generate four sets of orthogonal chaos-based signals, which can greatly increase the communication capacity. An integrated utility function is defined and a particle swarm algorithm is introduced to optimize each parameter of the system. The theoretical BER equation is derived and the system simulation is analyzed under the Additive White Gaussian Noise (AWGN) channel and Rayleigh fading channel. The integrated utility functions of different systems are also compared. The results show that the system has a lower BER and better integrated utility compared, and has a better practical application.
-
表 1 ECO-NS-MDCSK系统的映射规则(M=4)
二进制比特(${b_1},{b_2}$) 传输系数(${a_{1,1}},{a_{2,1}},{a_{3,1}},{a_{4,1}}$) 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 表 2 信道增益取值表
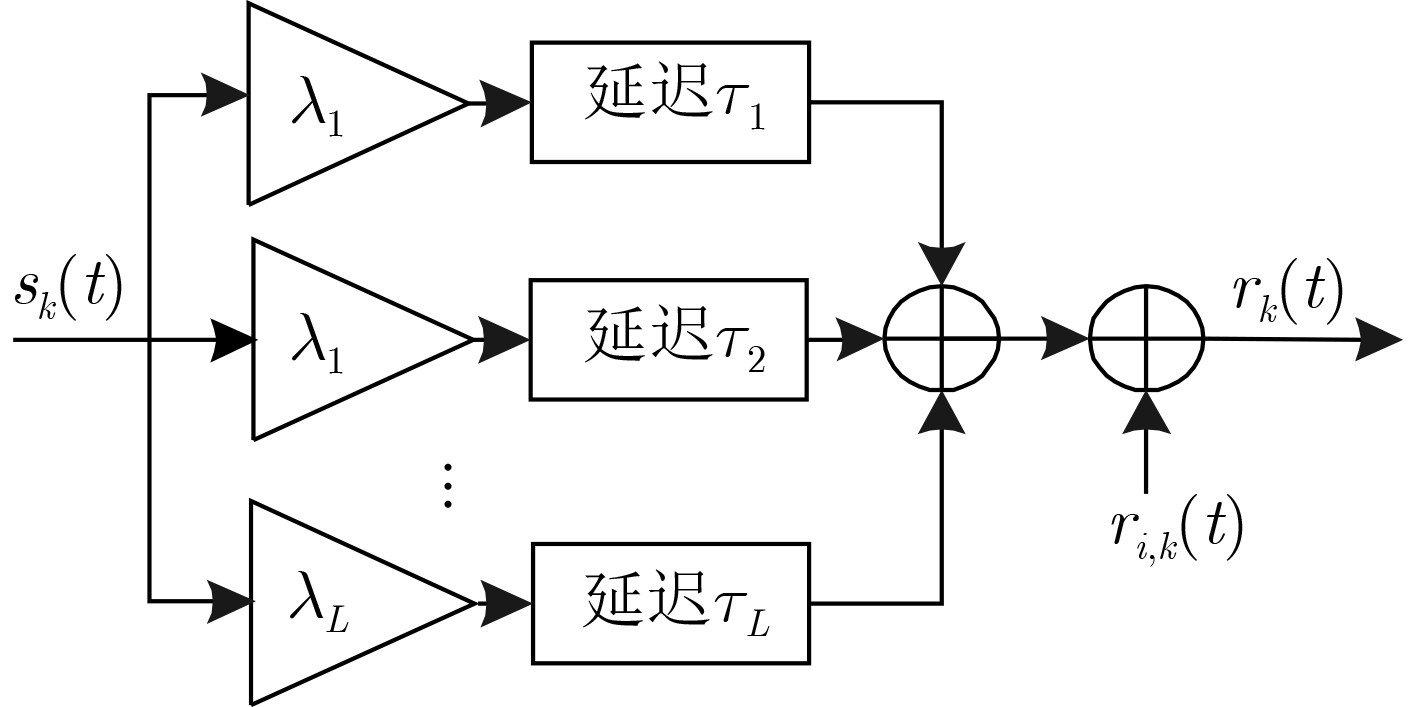
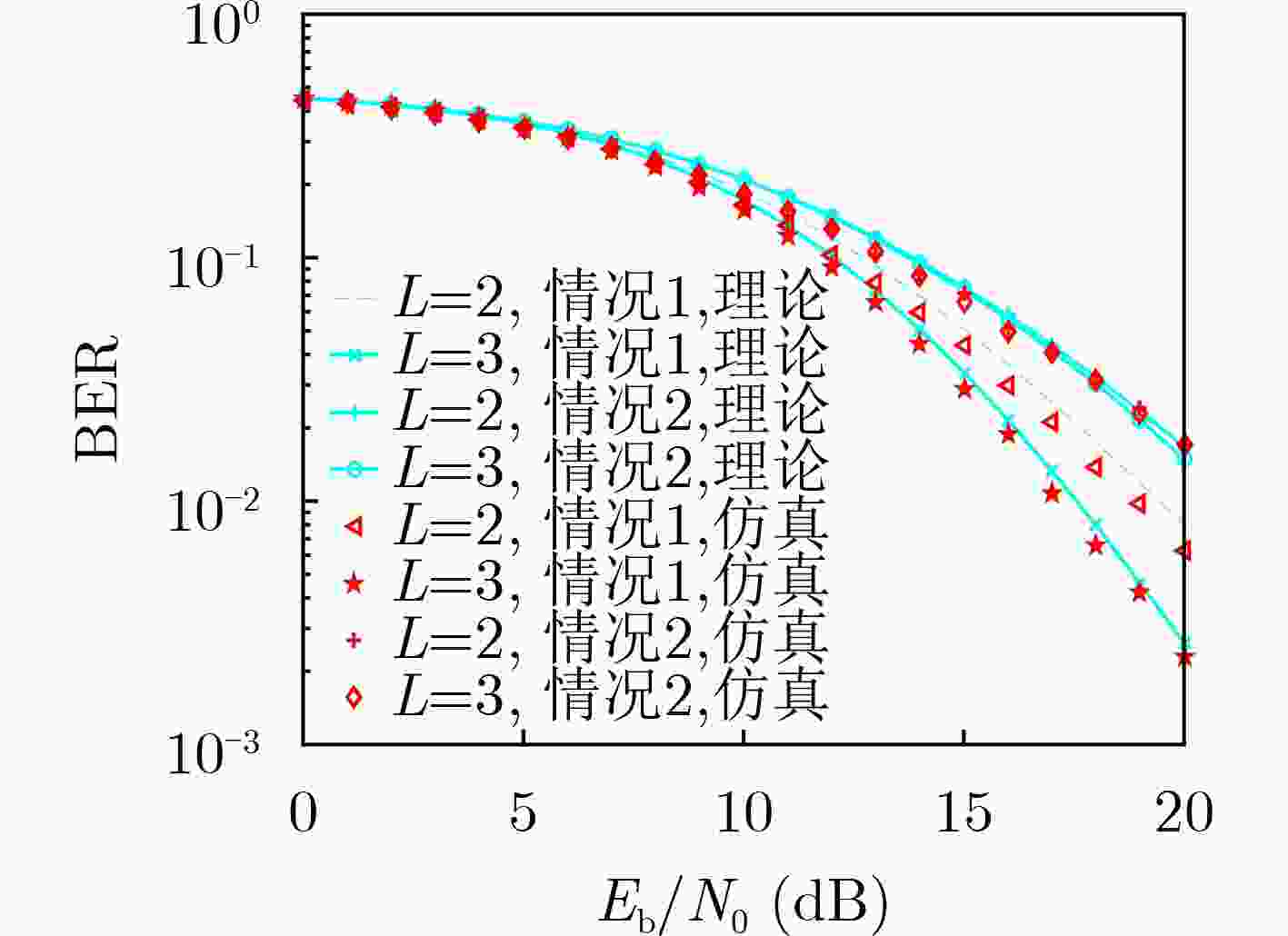
$L$ 情况1下的$E[\lambda _l^2]$ 情况2下的$E[\lambda _l^2]$ $L = 2$ 1/2,1/2 1/11,10/11 $L = 3$ 1/3,1/3,1/3 1/111,10/111,100/111 -
[1] 陈志刚, 梁涤青, 邓小鸿, 等. Logistic混沌映射性能分析与改进[J]. 电子与信息学报, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039CHEN Zhigang, LIANG Diqing, DENG Xiaohong, et al. Performance analysis and improvement of logistic chaotic mapping[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039 [2] CHEN Zuwei, ZHANG Lin, WU Zhiqiang, et al. Reliable and efficient sparse code spreading aided MC-DCSK transceiver design for multiuser transmissions[J]. IEEE Transactions on Communications, 2021, 69(3): 1480–1495. doi: 10.1109/TCOMM.2020.3040422 [3] XU Weikai, HUANG Tingting, and WANG Lin. Code-shifted differential chaos shift keying with code index modulation for high data rate transmission[J]. IEEE Transactions on Communications, 2017, 65(10): 4285–4294. doi: 10.1109/TCOMM.2017.2725261 [4] CHENG Guixian, WANG Lin, XU Weikai, et al. Carrier index differential chaos shift keying modulation[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2017, 64(8): 907–911. doi: 10.1109/TCSII.2016.2613093 [5] YE Lifen, CHEN Guanrong, and WANG Lin. Essence and advantages of FM-DCSK versus conventional spread-spectrum communication methods[J]. Circuits, Systems and Signal Processing, 2005, 24(5): 657–673. doi: 10.1007/s00034-005-2413-8 [6] KADDOUM G. Wireless chaos-based communication systems: A comprehensive survey[J]. IEEE Access, 2016, 4: 2621–2648. doi: 10.1109/ACCESS.2016.2572730 [7] HERCEG M, KADDOUM G, VRANJEŠ D, et al. Permutation index DCSK modulation technique for secure multiuser high-data-rate communication systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 2997–3011. doi: 10.1109/TVT.2017.2774108 [8] 蒋国平, 杨华, 段俊毅. 混沌数字调制技术研究进展[J]. 南京邮电大学学报:自然科学版, 2016, 36(1): 1–7. doi: 10.14132/j.cnki.1673-5439.2016.01.001JIANG Guoping, YANG Hua, and DUAN Junyi. Research progress on chaotic digital modulation technologies[J]. Journal of Nanjing University of Posts and Telecommunications:Natural Science Edition, 2016, 36(1): 1–7. doi: 10.14132/j.cnki.1673-5439.2016.01.001 [9] KOLUMBAN G, KENNEDY M P, JAKO Z, et al. Chaotic communications with correlator receivers: Theory and performance limits[J]. Proceedings of the IEEE, 2002, 90(5): 711–732. doi: 10.1109/JPROC.2002.1015003 [10] Sushchik M, Tsimring L S, Volkovskii A R. Performance analysis of correlation-based communication schemes utilizing chaos[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(12): 1684–1691. doi: 10.1109/81.899920 [11] KADDOUM G and GAGNON F. Performance analysis of STBC-CSK communication system over slow fading channel[J]. Signal Processing, 2013, 93(7): 2055–2060. doi: 10.1016/j.sigpro.2012.12.020 [12] QUYEN N X, DUONG T Q, and NALLANATHAN A. Modelling, analysis and performance comparison of two direct sampling DCSK receivers under frequency non-selective fading channels[J]. IET Communications, 2016, 10(11): 1263–1272. doi: 10.1049/iet-com.2015.1103 [13] HUANG Tingting, CHEN Wenyu, YANG Dongliang, et al. Design and performance analysis of multicarrier M-ary differential chaos shift keying system[C]. 2021 15th International Symposium on Medical Information and Communication Technology (ISMICT), Xiamen, China, 2021: 211–214. [14] 夏磊, 杨华, 宋玉蓉. 多用户载波索引差分混沌移位键控通信系统及性能分析[J]. 计算机工程, 2021, 47(5): 181–188. doi: 10.19678/j.issn.1000-3428.0057946XIA Lei, YANG Hua, and SONG Yurong. Multi-user carrier index differential chaos shift keying communication system and performance analysis[J]. Computer Engineering, 2021, 47(5): 181–188. doi: 10.19678/j.issn.1000-3428.0057946 [15] CAI Xiangming, XU Weikai, HONG Shaohua, et al. A trinal-code shifted differential chaos shift keying system[J]. IEEE Communications Letters, 2021, 25(3): 1000–1004. doi: 10.1109/LCOMM.2020.3041460 [16] YANG Hua, TANG W K S, CHEN Guanrong, et al. System design and performance analysis of orthogonal multi-level differential chaos shift keying modulation scheme[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2016, 63(1): 146–156. doi: 10.1109/TCSI.2015.2510622 [17] TIAN Dongping and SHI Zhongzhi. MPSO: Modified particle swarm optimization and its applications[J]. Swarm and Evolutionary Computation, 2018, 41: 49–68. doi: 10.1016/j.swevo.2018.01.011 [18] 张刚, 和华杰, 张鹏. 基于施密特正交化的降噪多载波相关延迟键控混沌通信系统[J]. 电子与信息学报, 2021, 43(7): 1930–1938. doi: 10.11999/JEIT200165ZHANG Gang, HE Huajie, and ZHANG Peng. NR-MC-CDSK chaotic communication system based on schmidt orthogonalization[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1930–1938. doi: 10.11999/JEIT200165 [19] 贺利芳, 吴雪霜, 张天骐. 正交多用户短参考差分混沌移位键控通信系统性能分析[J]. 电子与信息学报, 2020, 42(10): 2445–2453. doi: 10.11999/JEIT190778HE Lifang, WU Xueshuang, and ZHANG Tianqi. Performance analysis of orthogonal multiuser short reference differential chaos shift keying communication system[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2445–2453. doi: 10.11999/JEIT190778 [20] ZHANG Gang, DONG Jiangtao, and HE Lifang. A noise reduction orthogonal multi-user CDSK communication system based on frequency domain processing[J]. Annals of Telecommunications, 2022, 77(3): 237–250. doi: 10.1007/s12243-021-00873-9 -





 下载:
下载:
















 下载:
下载:
