Research on OFDM-IM Visible Light Communication System Based on Combination Index and Euclidean Distance
-
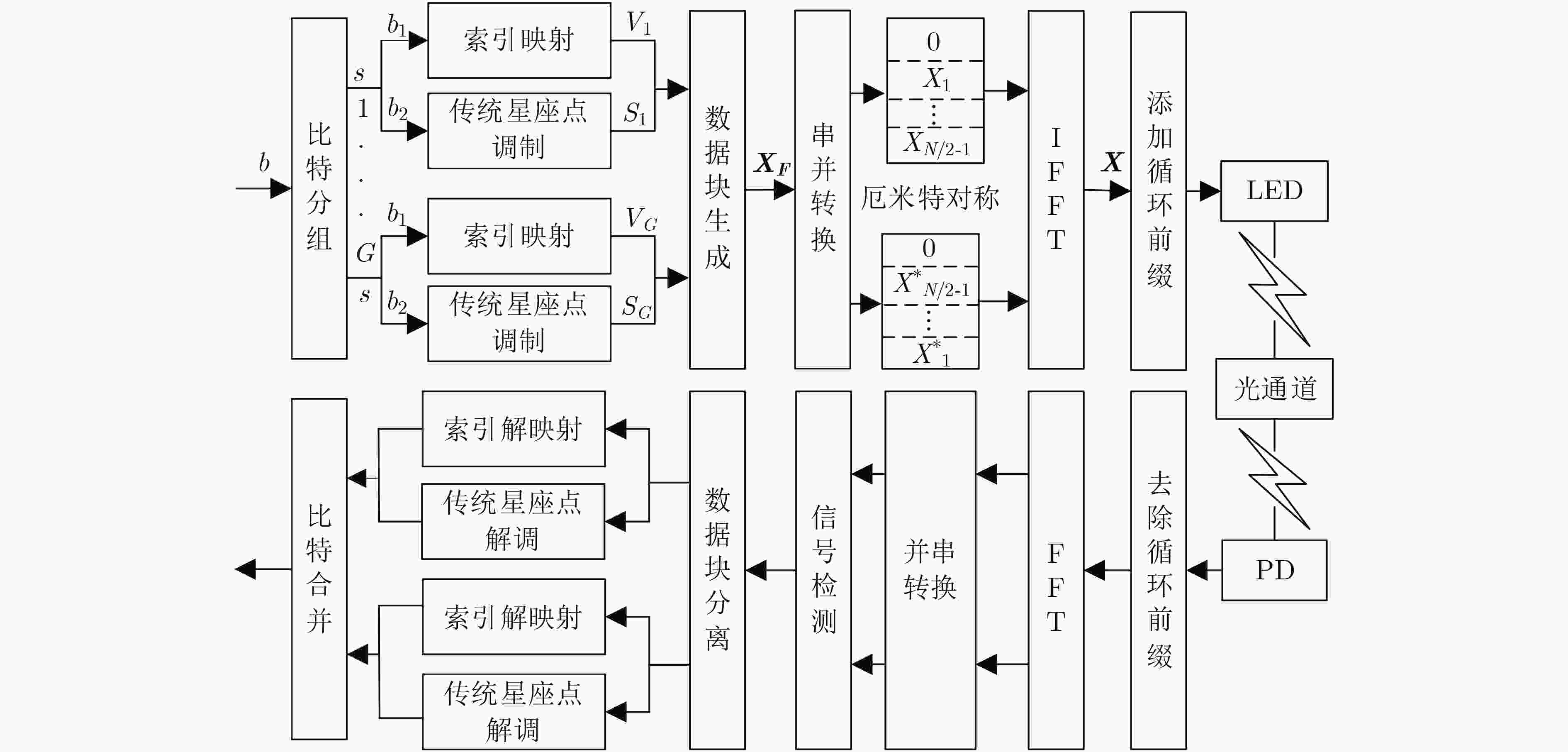
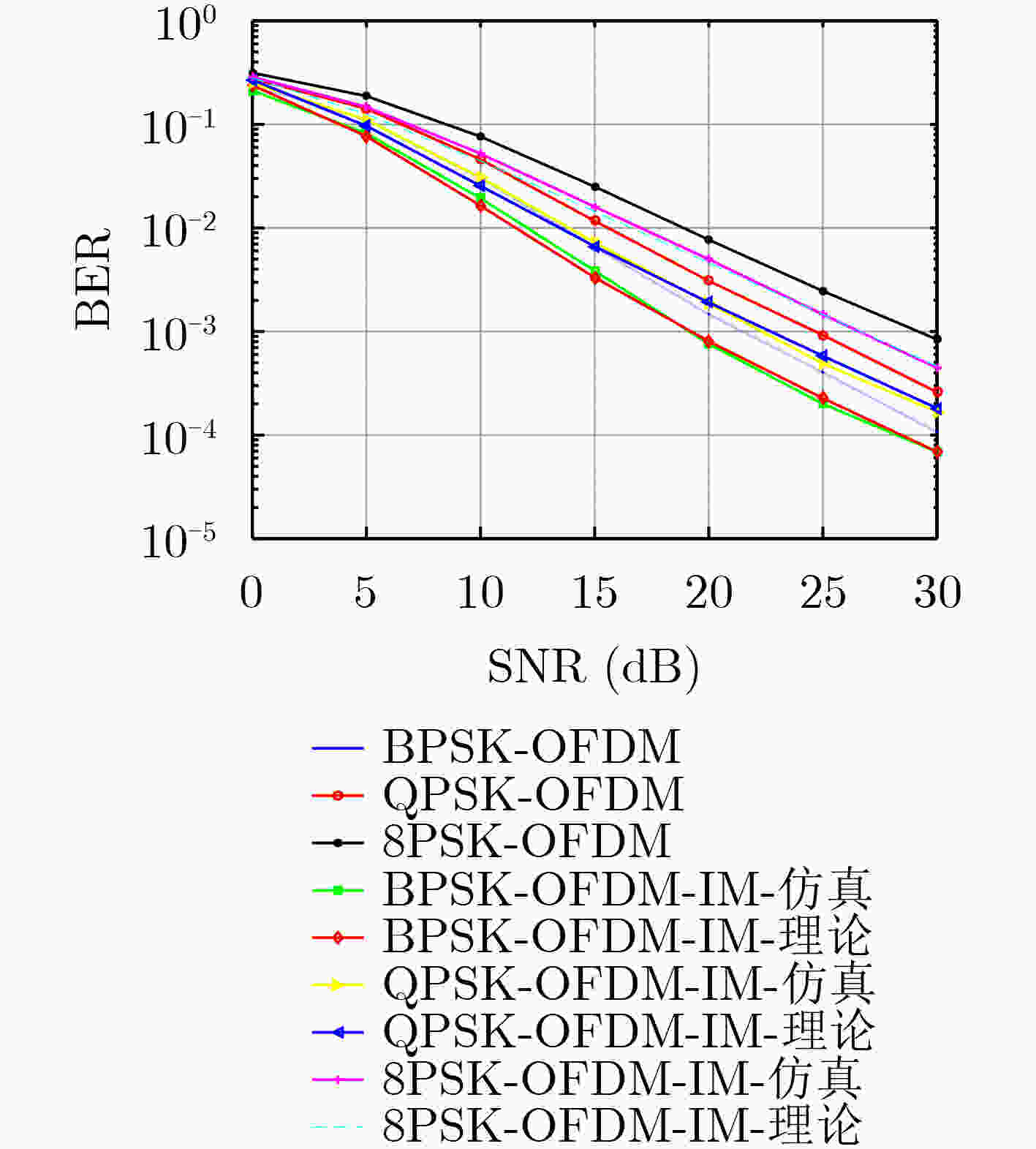
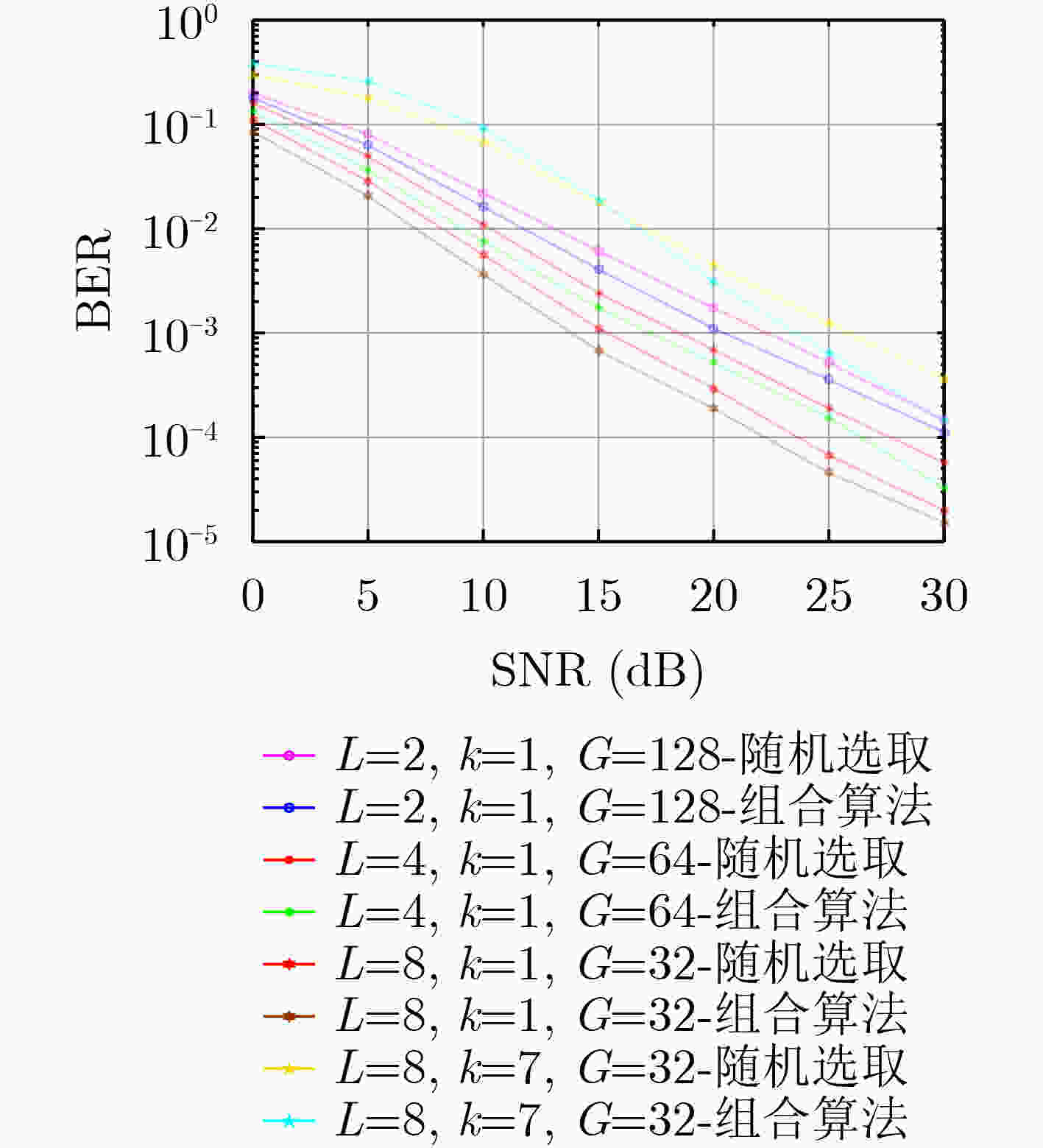
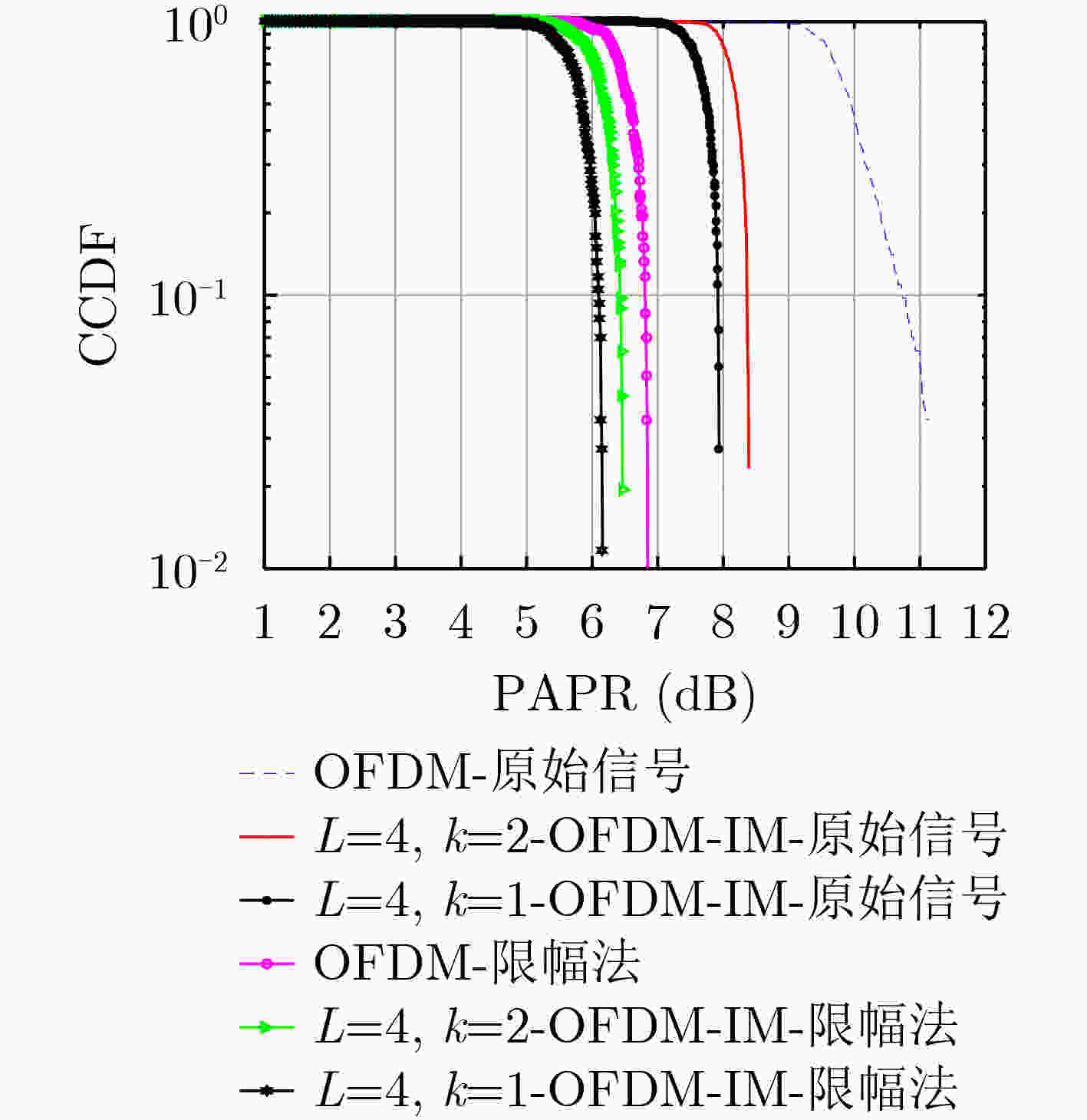
摘要: 直流偏置光正交频分复用系统(DCO-OFDM)存在较高的峰均比(PAPR)、易受多径干扰和噪声频偏等影响。因此该文将载波索引调制(IM)引入DCO-OFDM中,提出适合可见光通信(VLC)的DCO-OFDM-IM调制方案。该方案采用基于组合索引与欧氏距离相结合的信号映射约束模型对子载波进行分块组合索引,不仅可在信号域使用传统星座调制传递信息,还可通过频率域利用载波索引额外携带信息,有效改善了系统峰均比及误码率性能。推导了DCO-OFDM-IM系统的理论误码率(BER),利用蒙特卡罗方法对其进行仿真验证。结果表明:相对传统DCO-OFDM系统,当子载波数为256,调制阶数为4,系统误码率为10–3时,DCO-OFDM-IM系统所需信噪比平均改善了约2 dB;当误码率为10–3时,采用组合索引与欧氏距离相结合的算法较随机选取载波组合系统所需信噪比平均改善约2 dB;当系统互补累计分布函数(CCDF)为10–1时,DCO-OFDM-IM原始信号峰均比比DCO-OFDM下降了约2.4 dB。Abstract: DC-bias Optical-Orthogonal Frequency Division Multiplexing (DCO-OFDM) has a high Peak-to-Average Power Ratio (PAPR) and is susceptible to multipath interference and noise frequency bias. To address this challenge, carrier Index Modulation (IM) is introduced into DCO-OFDM and a DCO-OFDM-IM modulation scheme suitable for visible light communication is proposed. In this scheme, the signal mapping constraint model bases on the combination of composite index and Euclidian distance is used to perform block composite index of subcarriers, which can not only transfer information using traditional constellation modulation in the signal domain, but also carry additional information through the carrier index in the frequency domain, which improves effectively the system peak to average ratio and bit error rate performance. The theoretical bit error rate of DCO-OFDM-IM system is derived and verified by monte Carlo method. The results show that compared with traditional DCO-OFDM system, when the number of subcarriers is 256, the modulation order is 4, and the system bit error rate is 10–3, the required Signal-to-Noise Ratio (SNR) of DCO-OFDM-IM system is improved by about 2 dB on average. When the BER is 10–3, the required SNR of the combined index and Euclidian distance algorithm improved by 2 dB on average compared with the random carrier combination system. When the system Complementary Cumulative Distribution Function (CCDF) is 10–1, the average ratio of the original signal peaks of DCO-OFDM-IM is decreased by about 2.4 dB compared with that of DCO-OFDM.
-
表 1 基于最大化最小欧氏距离算法的OFDM-IM映射表
索引序号 索引比特 索引序列 信号子块 1 $ \left[ {0,0} \right] $ $ \left[ {1,2} \right] $ $ {\left[ {{X_i},{X_j},0,0} \right]^{\text{T}}} $ 2 $ \left[ {0,1} \right] $ $ \left[ {1,3} \right] $ $ {\left[ {{X_i},0,{X_j},0} \right]^{\text{T}}} $ 3 $ \left[ {1,0} \right] $ $ \left[ {1,4} \right] $ $ {\left[ {{X_i},0,0,{X_j}} \right]^{\text{T}}} $ 4 $ \left[ {1,1} \right] $ $ \left[ {2,4} \right] $ $ {\left[ {0,{X_i},0,{X_j}} \right]^{\text{T}}} $ 未用 $ \left[ {3,4} \right] $ $ \left[ {2,3} \right] $ 表 2 系统频谱效率对比与运行时间对比
系统 时间(s) 调制阶数 信噪比(dB) 频谱效率(bps/Hz) OFDM 0.106 BPSK 22 0.5 0.11 QPSK 25 1 0.121 8PSK 29 1.5 (4,2)-OFDM-IM 0.081 BPSK 18 0.5 0.085 QPSK 23 0.75 0.097 8PSK 26 1.75 (2,1)-OFDM-IM 0.04 QPSK 20 0.75 (4,1)-OFDM-IM 0.062 QPSK 16 0.5 (8,1)-OFDM-IM 0.107 QPSK 14 0.3125 (8,7)-OFDM-IM 0.118 QPSK 24 1.0625 -
[1] CHUN H, RAJBHANDARI S, FAULKNER G, et al. Optimum device and modulation scheme selection for optical wireless communications[J]. Journal of Lightwave Technology, 2021, 39(8): 2281–2287. doi: 10.1109/JLT.2021.3051379 [2] 叶新荣, 朱卫平, 张爱清, 等. OFDM系统双选择性慢衰落信道的压缩感知估计[J]. 电子与信息学报, 2015, 37(1): 169–174. doi: 10.11999/JEIT140247YE Xinrong, ZHU Weiping, ZHANG Aiqing, et al. Compressed sensing based on doubly-selective slow-fading channel estimation in OFDM systems[J]. Journal of Electronics &Information Technology, 2015, 37(1): 169–174. doi: 10.11999/JEIT140247 [3] 邵凯, 金庚, 王光宇, 等. 排列模式索引调制正交频分复用系统[J]. 电子与信息学报, 2021, 43(9): 2640–2646. doi: 10.11999/JEIT200248SHAO Kai, JIN Geng, WANG Guangyu, et al. Permutation-mode orthogonal frequency division multiplexing system with index modulation[J]. Journal of Electronics &Information Technology, 2021, 43(9): 2640–2646. doi: 10.11999/JEIT200248 [4] 彭聪, 许鹏, 陈翔, 等. MIMO-OFDM系统中各天线独立相位噪声的影响[J]. 电子与信息学报, 2017, 39(12): 2999–3003. doi: 10.11999/JEIT170260PENG Cong, XU Peng, CHEN Xiang, et al. Influence of independent phase noises on MIMO-OFDM systems[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2999–3003. doi: 10.11999/JEIT170260 [5] JIANG Tao, TANG Ming, LIN Rui, et al. Investigation of DC-biased optical OFDM with precoding matrix for visible light communications: Theory, simulations, and experiments[J]. IEEE Photonics Journal, 2018, 10(5): 1–16. doi: 10.1109/JPHOT.2018.2866952 [6] HUSSEIN H S and HAGAG M. Optical MIMO-OFDM with fully generalized index-spatial LED modulation[J]. IEEE Communications Letters, 2019, 23(9): 1556–1559. doi: 10.1109/LCOMM.2019.2926457 [7] 左家骏, 杨瑞娟, 李晓柏, 等. 基于索引调制OFDM雷达通信共享信号压缩感知方法研究[J]. 电子与信息学报, 2020, 42(12): 2976–2983. doi: 10.11999/JEIT190740ZUO Jiajun, YANG Ruijuan, LI Xiaobai, et al. A compressed sensing method for joint radar and communication system based on OFDM-IM signal[J]. Journal of Electronics &Information Technology, 2020, 42(12): 2976–2983. doi: 10.11999/JEIT190740 [8] 葛利嘉, 江治林, 冯胜, 等. 非正交-码索引调制方法[J]. 电子与信息学报, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023GE Lijia, JIANG Zhilin, FENG Sheng, et al. Non-orthogonal-code index modulation[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023 [9] VAN LUONG T and KO Y. Spread OFDM-IM with precoding matrix and low-complexity detection designs[J]. IEEE Transactions on Vehicular Technology, 2018, 67(12): 11619–11626. doi: 10.1109/TVT.2018.2872873 [10] NTOUN G D, KAPINAS V M, and KARAGIANNIDIS G K. On the optimal tone spacing for interference mitigation in OFDM-IM systems[J]. IEEE Communications Letters, 2017, 21(5): 1019–1022. doi: 10.1109/LCOMM.2017.2660479 [11] KIM K H. PAPR reduction in OFDM-IM using multilevel dither signals[J]. IEEE Communications Letters, 2019, 23(2): 258–261. doi: 10.1109/LCOMM.2019.2892103 [12] TUSHA A, DOĞAN S, and ARSLAN H. IQI mitigation for narrowband IoT systems with OFDM-IM[J]. IEEE Access, 2018, 6: 44626–44634. doi: 10.1109/ACCESS.2018.2864892J [13] LI Jun, DANG Shuping, WEN Miaowen, et al. Layered orthogonal frequency division multiplexing with index modulation[J]. IEEE Systems Journal, 2019, 13(4): 3793–3802. doi: 10.1109/JSYST.2019.2918068 [14] QING Hua, YU Hua, LIU Yun, et al. Distributed cooperative OFDM-IM system[J]. China Communications, 2020, 17(9): 167–176. doi: 10.23919/JCC.2020.09.013 [15] 赵辉, 莫谨荣, 王薇, 等. OFDM系统中基于压缩感知的非线性失真恢复研究[J]. 电子与信息学报, 2021, 43(7): 1907–1912. doi: 10.11999/JEIT20037ZHAO Hui, MO Jinrong, WANG Wei, et al. Research on nonlinear distortion recovery based on compressed sensing in OFDM system[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1907–1912. doi: 10.11999/JEIT20037 -





 下载:
下载:


 下载:
下载:
