一种分布式发电功率时间序列波动性量化评估方法

陈晨; 袁绍军; 尹兆磊; 贺晓红; 杨慢慢; 李润鑫

doi:10.11999/JEIT220096

一种分布式发电功率时间序列波动性量化评估方法

doi: 10.11999/JEIT220096

陈晨^{1, 2},
袁绍军¹,
尹兆磊^1, ,,
贺晓红¹,
杨慢慢¹,
李润鑫¹

1.
国网冀北电力有限公司承德供电公司承德 067000
2.
华北电力大学能源动力与机械工程学院保定 071066

详细信息

作者简介:
陈晨：男，工程师，研究方向为电网运行方式及分布式电源管理

袁绍军：男，高级工程师，研究方向为电网调度及新能源运行管理

尹兆磊：男，工程师，研究方向为电网运行方式及新能源管理

贺晓红：女，高级工程师，研究方向为电网运行

杨慢慢：女，高级工程师，研究方向为无功电压管理

李润鑫：男，高级工程师，研究方向为电网调度运行

通讯作者:
尹兆磊　cdgrid@163.com

中图分类号: TM614
计量
- 文章访问数: 566
- HTML全文浏览量: 337
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2022-01-24
- 修回日期: 2022-03-17
- 网络出版日期: 2022-06-25
- 刊出日期: 2022-11-14

A Fluctuation Quantitative Evaluation Method for Distributed Energy Power Time Series

1.
State Grid Jibei Electric Power Company Limited, Chengde 067000, China
2.
School of Energy Power Mechanical Engineering, North China Electric Power University, Baoding 071066, China

摘要

摘要: 未来智能电网将接纳越来越多的分布式能源，而分布式能源的广泛接入具有提高系统的能源效率、经济性、韧性以及可持续性的潜力。然而，以风力发电和光伏发电为主的分布式能源由于其固有的波动特性，在大规模接入电网时会给系统带来诸多问题。因此，定量刻画分布式发电功率的波动性对于现代电力系统而言至关重要。基于此，该文借助时间窗、包络线和勒贝格积分，通过提取分布式发电功率中高频信息和变化趋势的波动性特征，定义了量化分布式发电功率波动性的指标——波动率。通过检验风电功率时间序列的波动性、验证平滑效应以及与预测误差和已有指标进行对比分析，验证了所提出的波动率在衡量分布式发电功率波动性的有效性。
- 分布式发电 /
- 时间序列 /
- 波动性 /
- 包络线 /
- 勒贝格积分
Abstract: Future smart grid will incorporate an increasing number of Distributed Energy Resources (DERs), which have the potential to enhance the system energy efficiency, economics, resilience, and sustainability. However, The DERs, dominated by wind power and photovoltaic power generation, would lead to many problems for a power system with large-scale DERs integrated due to their inherent fluctuation characteristic. Therefore, quantitatively evaluating the fluctuation level of the DERs’ power is of great importance for modern power system. To this end, by defining time window, using envelope and Lebesgue integration theory, the fluctuation quantitative index of DERs’ power—fluctuation rate—is defined by extracting the fluctuations of high frequency information and trends of the DER’s output power time series. The validity of the fluctuation rate for measuring the fluctuation of DERs’ power is validated by testing the fluctuation, smoothing effects of wind power and conducting comparative analysis with prediction error and existing fluctuation index.
- Distributed energy /
- Time series /
- Fluctuation /
- Envelope /
- Lebesgue integration

HTML全文

图 1 不同时间序列及其上下包络线

下载: 全尺寸图片幻灯片

图 2 波动性不同的风电功率时间序列

下载: 全尺寸图片幻灯片

图 3 风电功率时间序列a和b在不同l选取下r的变化

下载: 全尺寸图片幻灯片

图 4 风力机汇聚出力下的r

下载: 全尺寸图片幻灯片

图 5 高频波动基本相同但变化趋势波动不同的风电功率时间序列e和f

下载: 全尺寸图片幻灯片

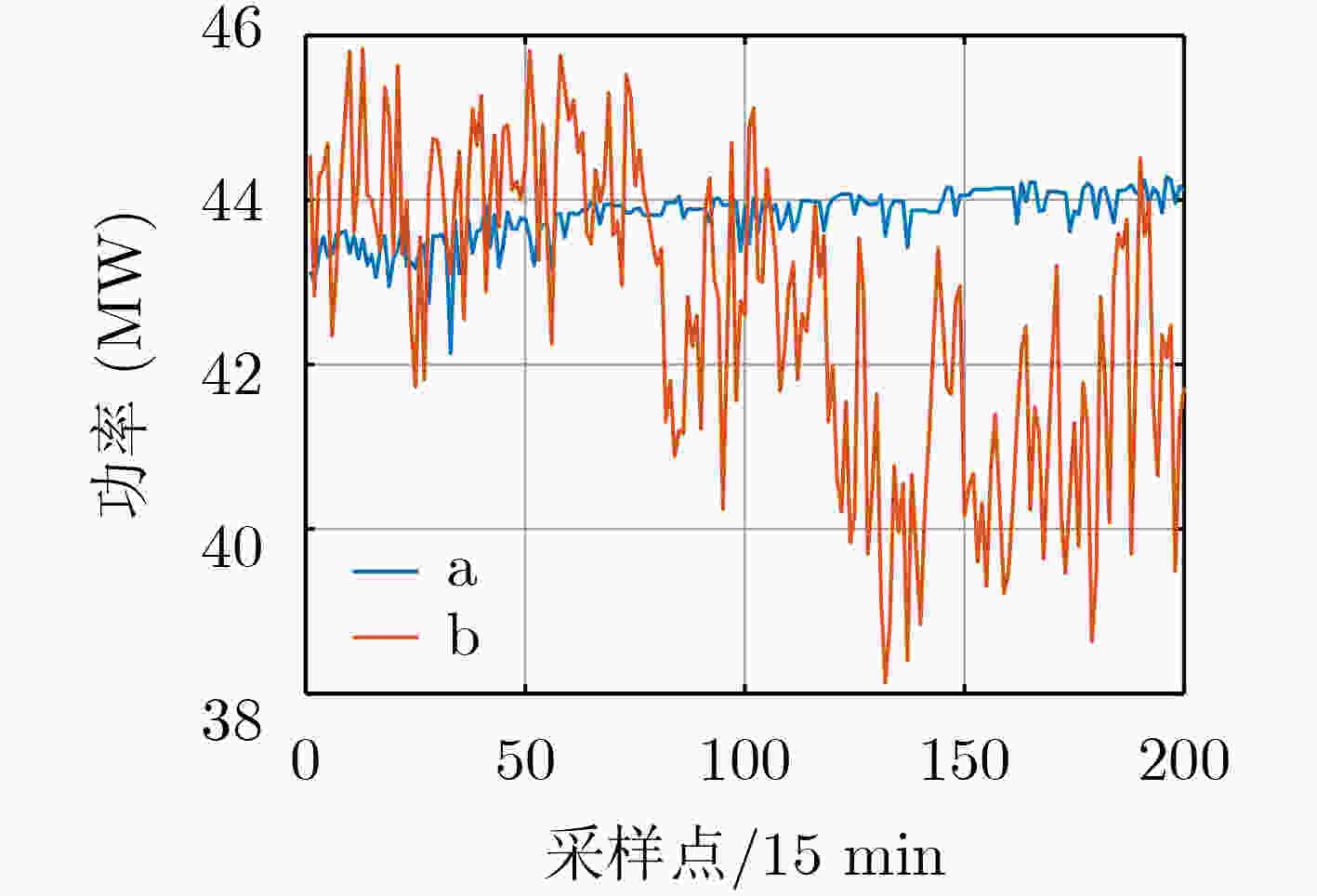
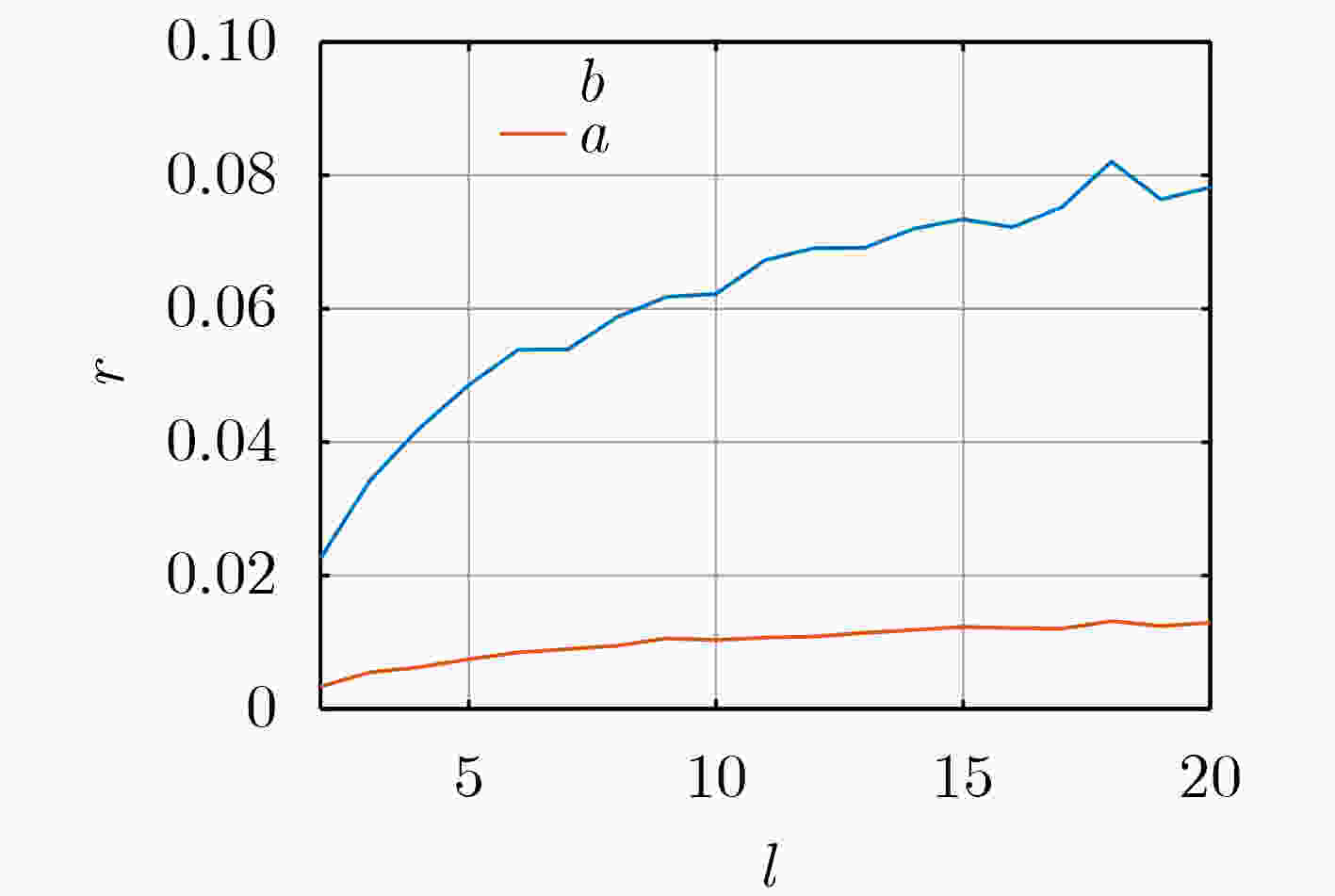
表 1 序列a和b的不同波动性衡量指标值和预测RMES

序列	波动率r	文献[17]指标	文献[18]指标	文献[19]指标	持续预测法(%)	ARMA预测法(%)
a	0.0061	0.0105	0.0019	0.6414	15.41	12.23
b	0.0373	0.0462	0.0085	1.6183	22.62	17.48

下载: 导出CSV

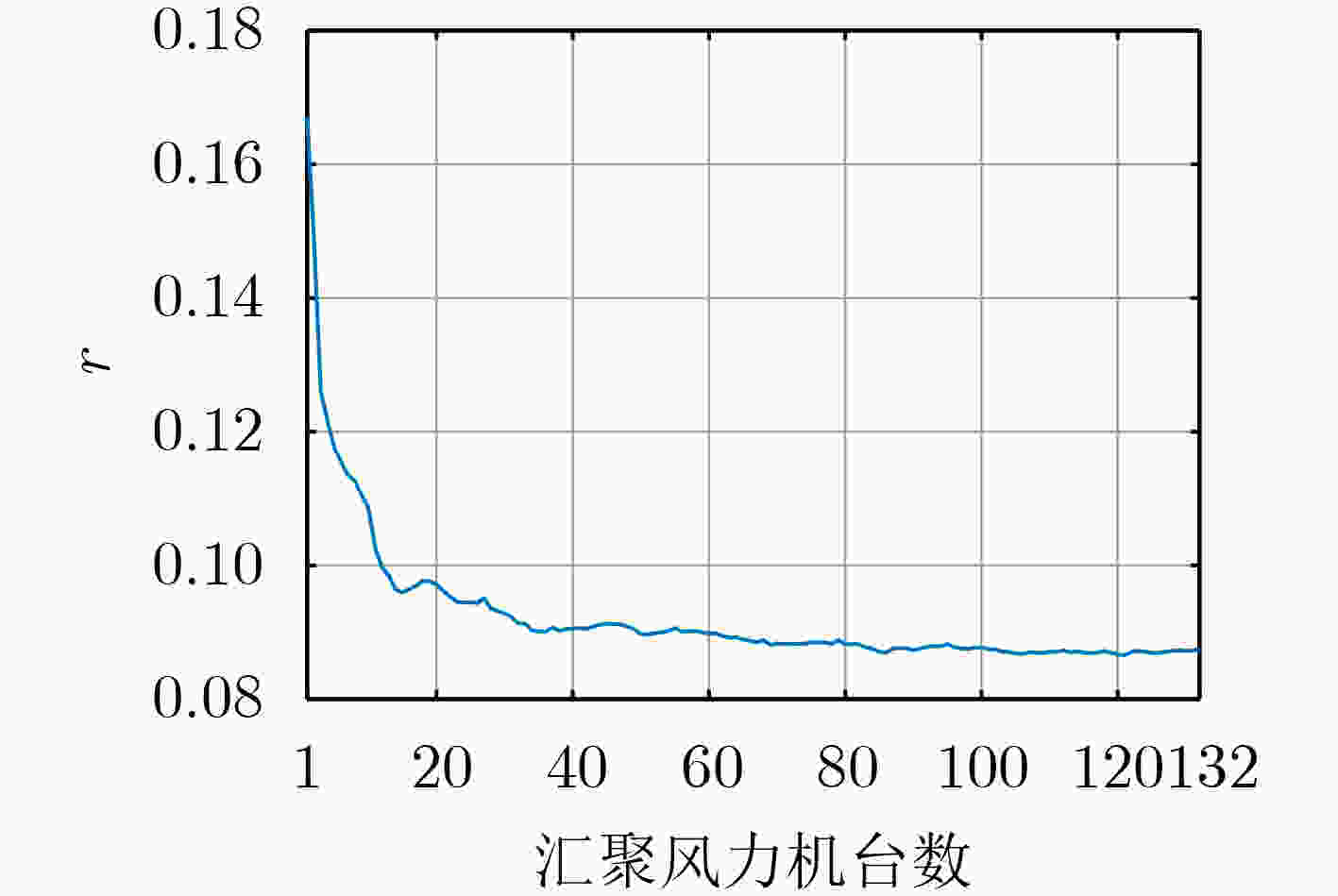
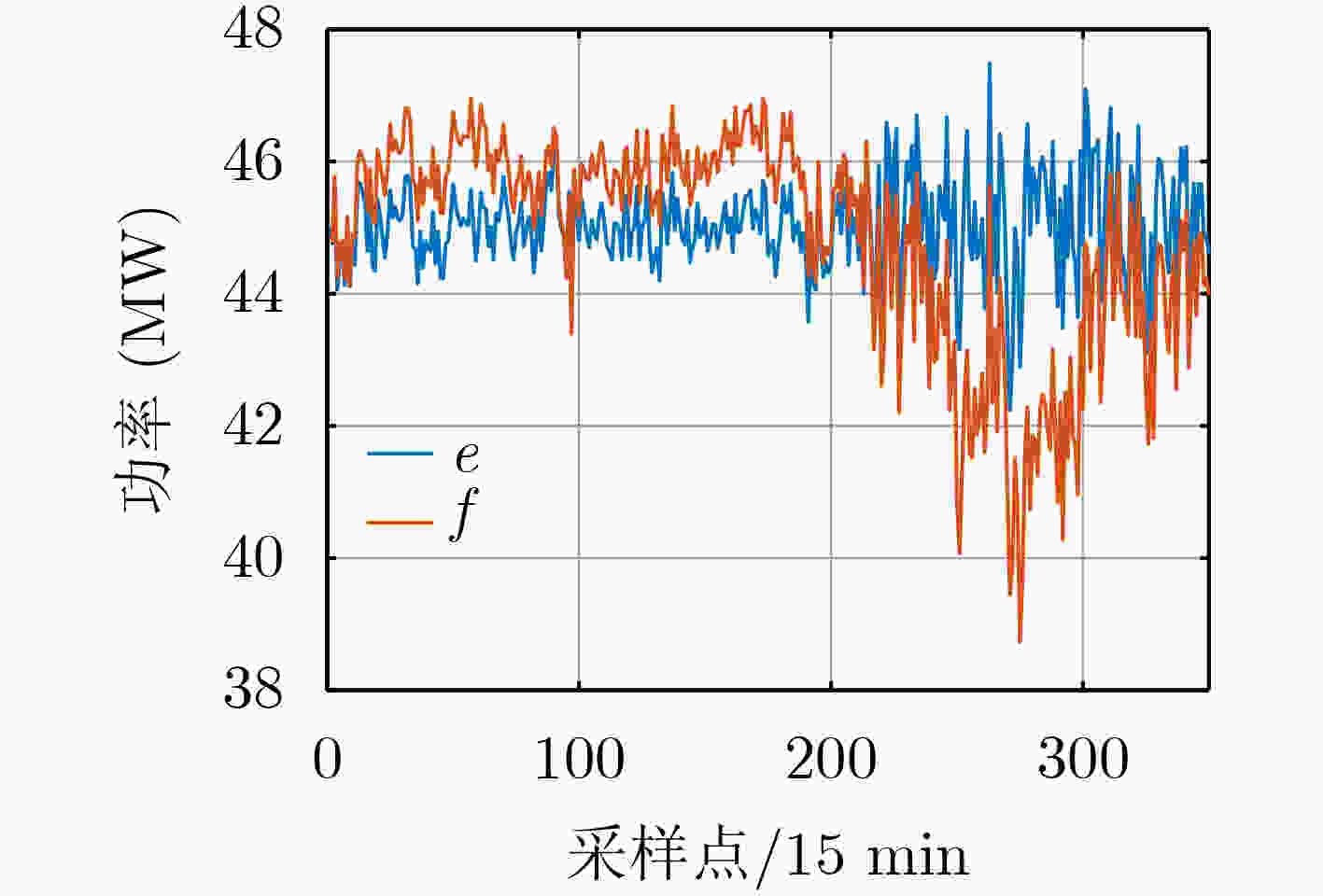
表 2 不同装机容量和时间长度下风电功率时间序列的波动性对比验证

	c	d
本文r值	0.0342	0.0095
文献[17] r值	0.0383	0.0144
文献[18] r值	0.0078	0.0023
文献[19] r值	1.5372	0.8590
持续预测法RMSE(%)	21.32	16.58
ARMA预测法RMSE(%)	16.86	14.17
文献[13]预测法RMSE(%)	11.50	8.76
文献[25]预测法RMSE(%)	15.43	9.89
文献[26]预测法RMSE(%)	12.71	8.84

下载: 导出CSV

表 3 两个风电功率时间序列的不同波动性衡量指标对比

	e	f
本文${r_1}$值	0.0404	0.0397
本文${r_2}$值	0.0270	0.0601
本文r值	0.0305	0.0499
文献[17] r值	0.0324	0.0308
文献[18] r值	0.0074	0.0065
持续预测法RMSE(%)	20.41	22.33
ARMA预测法RMSE(%)	14.28	18.94
文献[13]预测法RMSE(%)	10.07	13.04
文献[25]预测法RMSE(%)	14.13	16.33
文献[26]预测法RMSE(%)	11.77	14.90

下载: 导出CSV

参考文献(26)

[1]	CHEN Yulin, QI Donglian, DONG Hangning, et al. A FDI attack-resilient distributed secondary control strategy for islanded microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 1929–1938. doi: 10.1109/TSG.2020.3047949
[2]	ACKERMANN T. Wind power in power systems[J]. IEEE Power Engineering Review, 2013, 22(12): 23–27.
[3]	CHEN Yulin, LI Chaoyong, QI Donglian, et al. Distributed event-triggered secondary control for islanded microgrids with proper trigger condition checking period[J]. IEEE Transactions on Smart Grid, 2022, 13(2): 837–848. doi: 10.1109/TSG.2021.3115180
[4]	李俊, 王振宇, 向洁. 分布式蓄热电锅炉对弃风电量的消纳能力评估[J]. 电力科学与技术学报, 2021, 36(1): 185–191. doi: 10.19781/j.issn.1673-9140.2021.01.021 LI Jun, WANG Zhenyu, and XIANG Jie. Study on ability of distributed electric boilers with thermal storage in abandoned wind power consumption[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 185–191. doi: 10.19781/j.issn.1673-9140.2021.01.021
[5]	WANG Jiangfeng, SUN Kai, WU Hongfei, et al. Hybrid connected unified power quality conditioner integrating distributed generation with reduced power capacity and enhanced conversion efficiency[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 12340–12352. doi: 10.1109/TIE.2020.3040687
[6]	肖创英, 汪宁渤, 陟晶, 等. 甘肃酒泉风电出力特性分析[J]. 电力系统自动化, 2010, 34(17): 64–67. XIAO Ghuangying, WANG Ningbo, ZHI Jing, et al. Power characteristics of Jiuquan wind power base[J]. Automation of Electric Power Systems, 2010, 34(17): 64–67.
[7]	林卫星, 文劲宇, 艾小猛, 等. 风电功率波动特性的概率分布研究[J]. 中国电机工程学报, 2012, 32(1): 38–46. doi: 10.13334/j.0258-8013.pcsee.2012.01.010 LIN Weixing, WEN Jinyu, AI Xiaomeng, et al. Probability density function of wind power variations[J]. Proceedings of the CSEE, 2012, 32(1): 38–46. doi: 10.13334/j.0258-8013.pcsee.2012.01.010
[8]	张宁宇, 周前, 刘建坤. 江苏海上、沿海和内陆风电出力及波动特性分析[J]. 中国电力, 2020, 53(7): 18–23. ZHANG Ningyu, ZHOU Qian, and LIU Jiankun. Output and fluctuation characteristics of off-shore, coastal and inland wind farms in Jiangsu province[J]. Electric Power, 2020, 53(7): 18–23.
[9]	崔杨, 穆钢, 刘玉, 等. 风电功率波动的时空分布特性[J]. 电网技术, 2011, 35(2): 110–114. doi: 10.13335/j.1000-3673.pst.2011.02.017 CUI Yang, MU Gang, LIU Yu, et al. Spatiotemporal distribution characteristic of wind power fluctuation[J]. Power System Technology, 2011, 35(2): 110–114. doi: 10.13335/j.1000-3673.pst.2011.02.017
[10]	周统汉, 陈峦, 李坚. 基于有限混合Laplace模型的风功率波动特性研究[J]. 电网技术, 2017, 41(2): 543–550. doi: 10.13335/j.1000-3673.pst.2016.0844 ZHOU Tonghan, CHEN Luan, and LI Jian. Wind power fluctuation characteristic analysis based on finite Laplace mixture model[J]. Power System Technology, 2017, 41(2): 543–550. doi: 10.13335/j.1000-3673.pst.2016.0844
[11]	SORENSEN P, CUTULULIS N A, VIGUERAS-RODRIGUEZ A, et al. Power fluctuations from large wind farms[J]. IEEE Transactions on Power Systems, 2007, 22(3): 958–965. doi: 10.1109/TPWRS.2007.901615
[12]	SUNDARARAJAN A and SARWAT A I. Evaluation of missing data imputation methods for an enhanced distributed PV generation prediction[C]. Proceedings of Future Technologies Conference 2019, San Francisco: USA, 2020: 56–68.
[13]	CHENG Lilin, ZANG Haixiang, XU Yan, et al. Augmented convolutional network for wind power prediction: A new recurrent architecture design with spatial-temporal image inputs[J]. IEEE Transactions on Industrial Informatics, 2021, 17(10): 6981–6993. doi: 10.1109/TII.2021.3063530
[14]	杨茂, 陈郁林, 魏治成. 基于EEMD去噪和集对理论的风功率实时预测研究[J]. 太阳能学报, 2018, 39(5): 1440–1448. YANG Mao, CHEN Yulin, and WEI Zhicheng. Real-time prediction for wind power based on EEMD denoising and theory of spa[J]. Acta Energiae Solaris Sinica, 2018, 39(5): 1440–1448.
[15]	BANAKAR H and OOI B T. Clustering of wind farms and its sizing impact[J]. IEEE Transactions on Energy Conversion, 2009, 24(4): 935–942. doi: 10.1109/TEC.2008.2001454
[16]	YE Yida, QIAO Ying, LU Zongxiang, et al. Offshore wind power outputs in multiple temporal and spatial scales[C]. Proceedings of 2014 International Conference on Power System Technology, Chengdu, China, 2014: 2781–2787.
[17]	杨茂, 陈郁林. 风电功率波动特性定量刻画及应用研究[J]. 太阳能学报, 2019, 40(6): 1771–1779. YANG Mao and CHEN Yulin. A study for quantitative characterization of wind power fluctuations and its applications[J]. Acta Energiae Solaris Sinica, 2019, 40(6): 1771–1779.
[18]	ZHOU Ziqiang, PENG Shu, CHEN Yulin, et al. Quantitative characterization of wind power fluctuation[C]. Proceedings of 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 2020: 3089–3094.
[19]	DAI Juchuan, CAO Junwei, LIU Deshun, et al. Power fluctuation evaluation of large-scale wind turbines based on SCADA data[J]. IET Renewable Power Generation, 2017, 11(4): 395–402. doi: 10.1049/iet-rpg.2016.0124
[20]	钟佑明, 金涛, 秦树人. 希尔伯特-黄变换中的一种新包络线算法[J]. 数据采集与处理, 2005, 20(1): 13–17. doi: 10.3969/j.issn.1004-9037.2005.01.003 ZHONG Youming, JIN Tao, and QIN Shuren. New envelope algorithm for Hilbert-Huang transform[J]. Journal of Data Acquisition &Processing, 2005, 20(1): 13–17. doi: 10.3969/j.issn.1004-9037.2005.01.003
[21]	张纪平. Lebesgue积分迫敛性定理及其应用[J]. 黑河学院学报 2013, 4(5): 117–118. ZHANG Jiping. Lebesgue squeeze theorem and its applications[J]. Journal of Heihe University, 2013, 33(5): 117–118.
[22]	李丽, 叶林. 基于改进持续法的短期风电功率预测[J]. 农业工程学报, 2010, 26(12): 182–187. doi: 10.3969/j.issn.1002-6819.2010.12.031 LI Li and YE Lin. Short-term wind power forecasting based on an improved persistence approach[J]. Transactions of the CSAE, 2010, 26(12): 182–187. doi: 10.3969/j.issn.1002-6819.2010.12.031
[23]	刘帅, 朱永利, 张科, 等. 基于误差修正ARMA-GARCH模型的短期风电功率预测[J]. 太阳能学报, 2020, 41(10): 268–275. LIU Shuai, ZHU Yongli, ZHANG Ke, et al. Short-term wind power forecasting based on error correction ARMA-GARCH model[J]. Acta Energiae Solaris Sinica, 2020, 41(10): 268–275.
[24]	YANG Mao, ZHANG Luobin, CUI Yang, et al. Investigating the wind power smoothing effect using set pair analysis[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1161–1172. doi: 10.1109/TSTE.2019.2920255
[25]	杨茂, 陈郁林. 基于EMD分解和集对分析的风电功率实时预测[J]. 电工技术学报, 2016, 31(21): 86–93. doi: 10.19595/j.cnki.1000-6753.tces.2016.21.010 YANG Mao and CHEN Yulin. Real-time prediction for wind power based on EMD and set pair analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 86–93. doi: 10.19595/j.cnki.1000-6753.tces.2016.21.010
[26]	李大中, 李颖宇. 基于深度学习与误差修正的超短期风电功率预测[J]. 太阳能学报, 2021, 42(12): 200–205. doi: 10.19912/j.0254-0096.tynxb.2019-1464 LI Dazhong and LI Yingyu. Ultra-short-term wind power prediction based on deep learning and error correction[J]. Acta Energiae Solaris Sinica, 2021, 42(12): 200–205. doi: 10.19912/j.0254-0096.tynxb.2019-1464