A Deep Reinforcement Learning Communication Jamming Resource Allocation Algorithm Fused with Noise Network
-
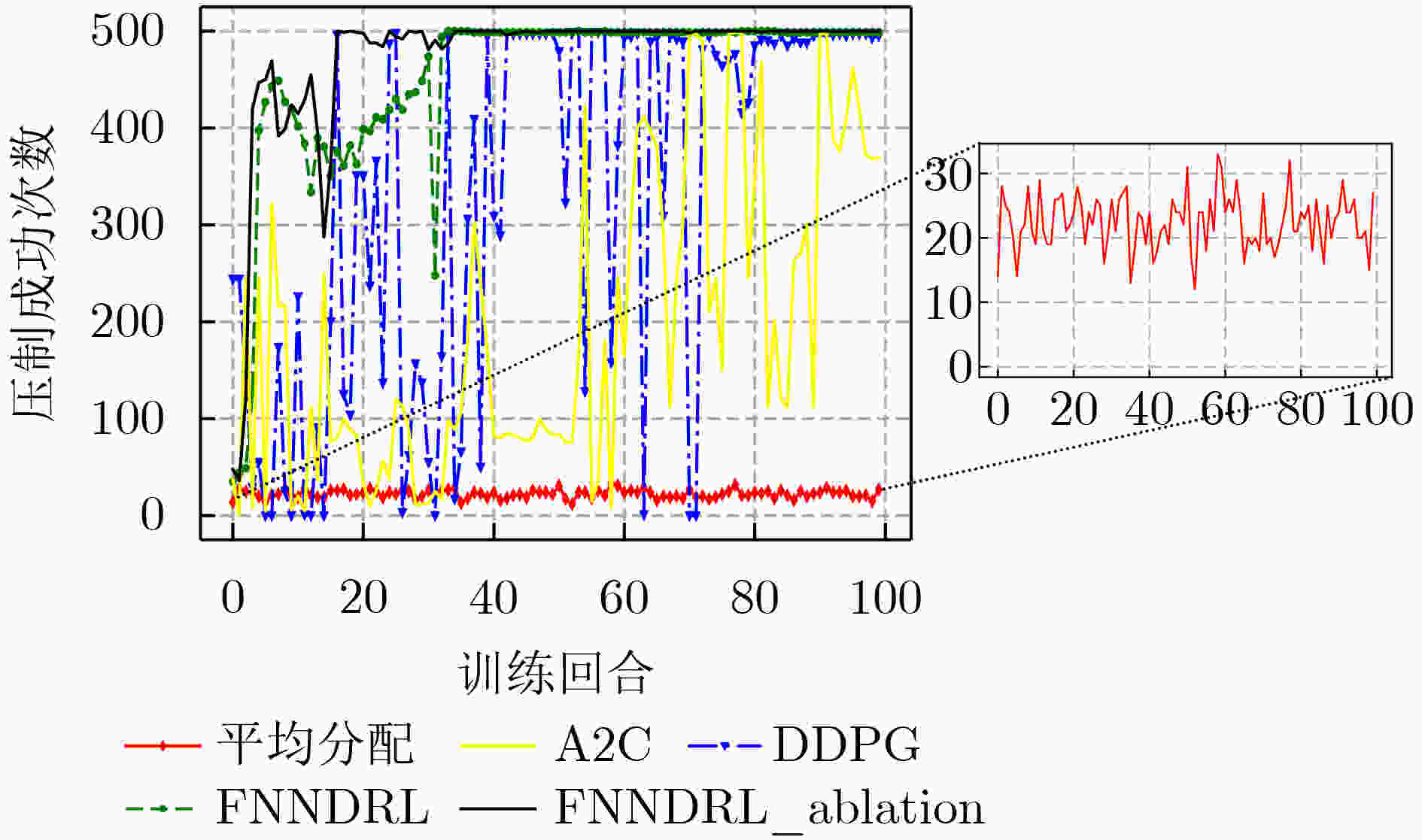
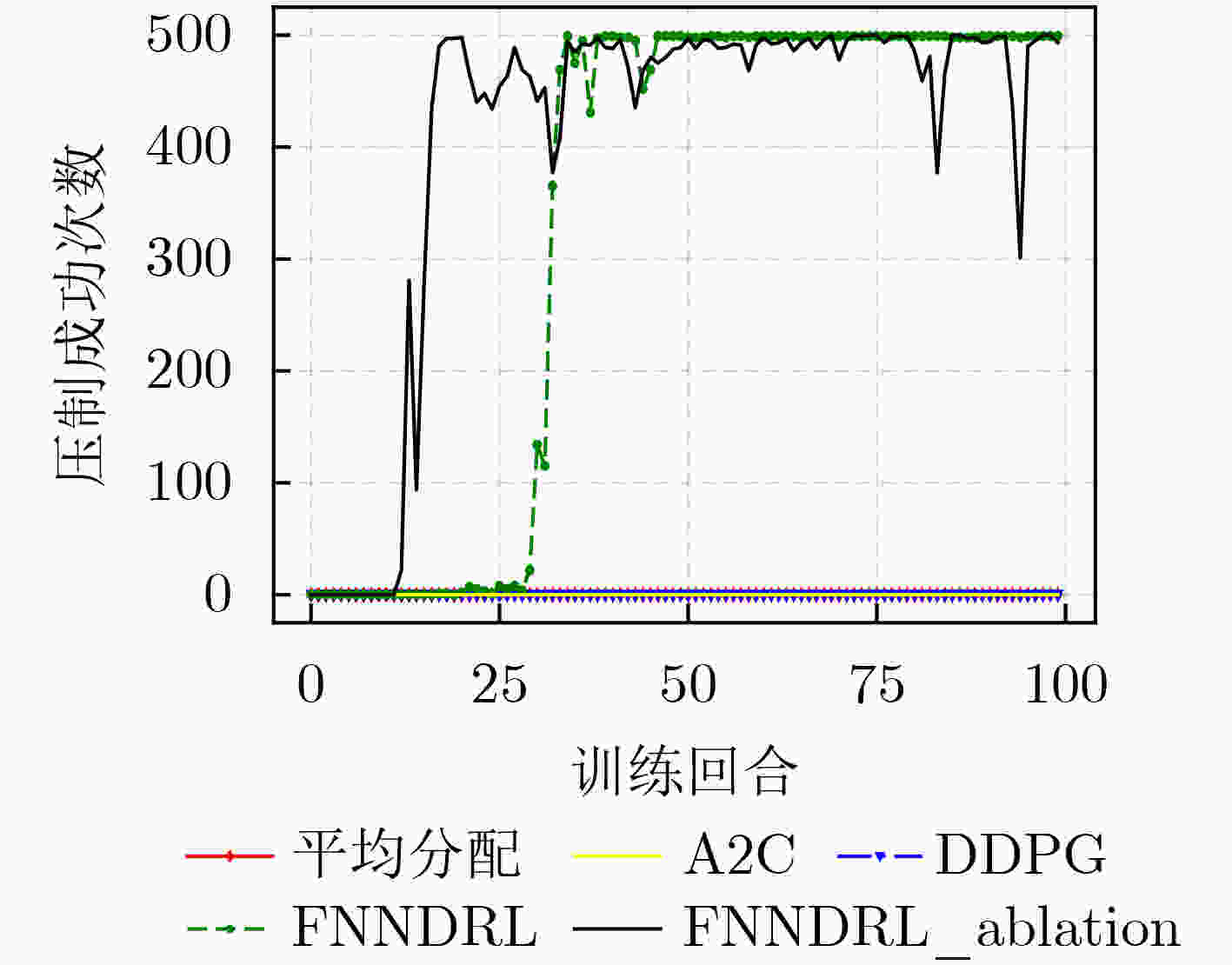
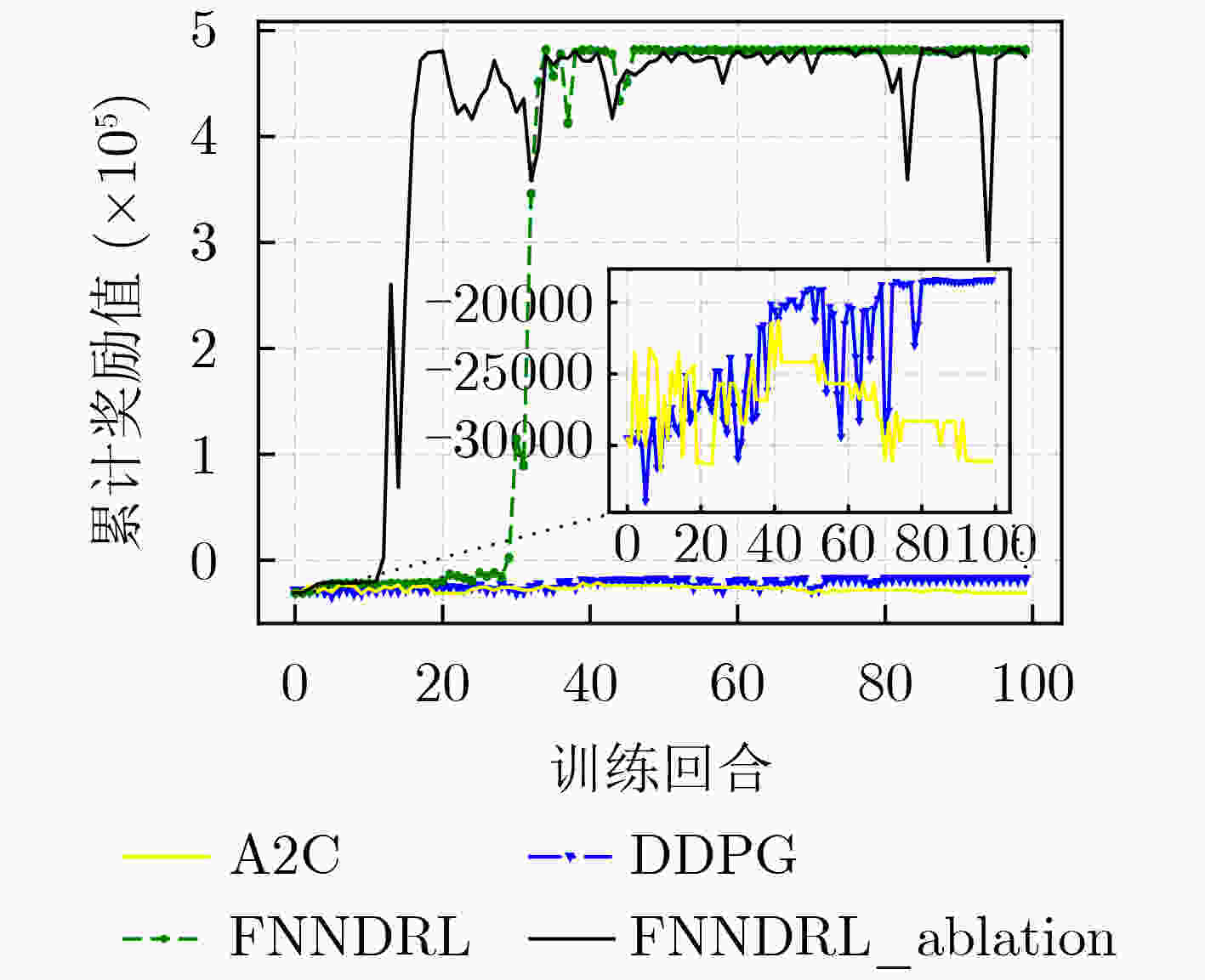
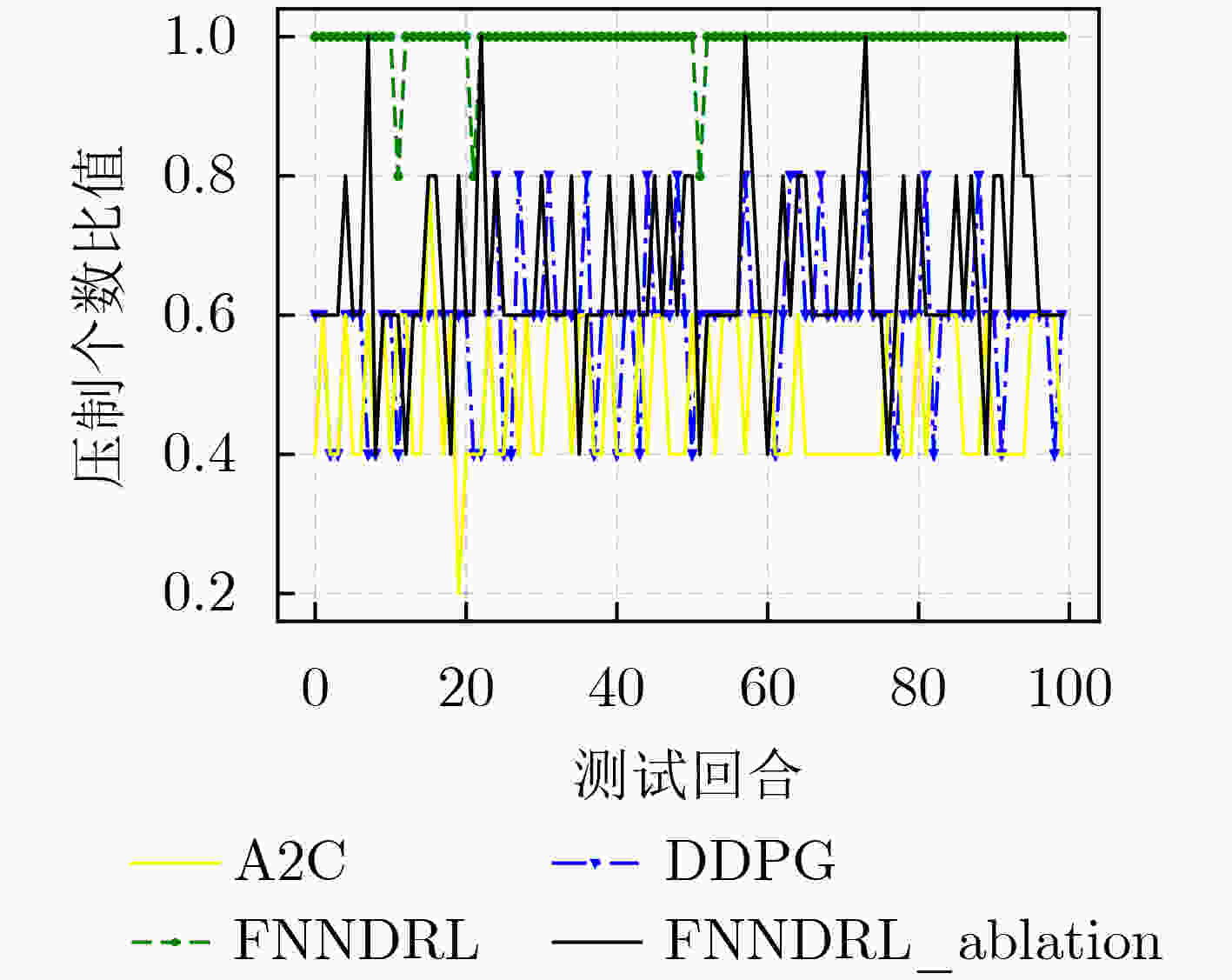
摘要: 针对传统干扰资源分配算法在处理非线性组合优化问题时需要较完备的先验信息,同时决策维度小,无法满足现代通信对抗要求的问题,该文提出一种融合噪声网络的深度强化学习通信干扰资源分配算法(FNNDRL)。借鉴噪声网络的思想,该算法设计了孪生噪声评估网络,在避免Q值高估的基础上,通过提升评估网络的随机性,保证了训练过程的探索性;基于概率熵的物理意义,设计了基于策略分布熵改进的策略网络损失函数,在最大化累计奖励的同时最大化策略分布熵,避免策略优化过程中收敛到局部最优。仿真结果表明,该算法在解决干扰资源分配问题时优于所对比的平均分配和强化学习方法,同时算法稳定性较高,对高维决策空间适应性强。Abstract: To solve the problem that the traditional jamming resource allocation algorithm needs relatively complete prior information when dealing with nonlinear combinatorial optimization problems, and meanwhile, the decision dimension is small, which can not meet the requirements of modern communication countermeasures, a Deep Reinforcement Learning communication jamming resource allocation algorithm Fused with Noise Network (FNNDRL) is proposed. Using the idea of noise network for reference, twin noise evaluation network, which can avoid the overestimation of Q value and improve the randomness of evaluation network to ensure the exploration of training process is designed by the algorithm. Based on the physical significance of the probability entropy, an improved strategy network loss function based on the strategy distribution entropy is designed to maximize the cumulative reward and the strategy distribution entropy to avoid convergence to local optimal in the process of strategy optimization. The simulation results show that the proposed algorithm is superior to the average allocation and reinforcement learning methods in solving the problem of jamming resource allocation. Meanwhile, the algorithm has high stability and strong adaptability to high-dimensional decision space.
-
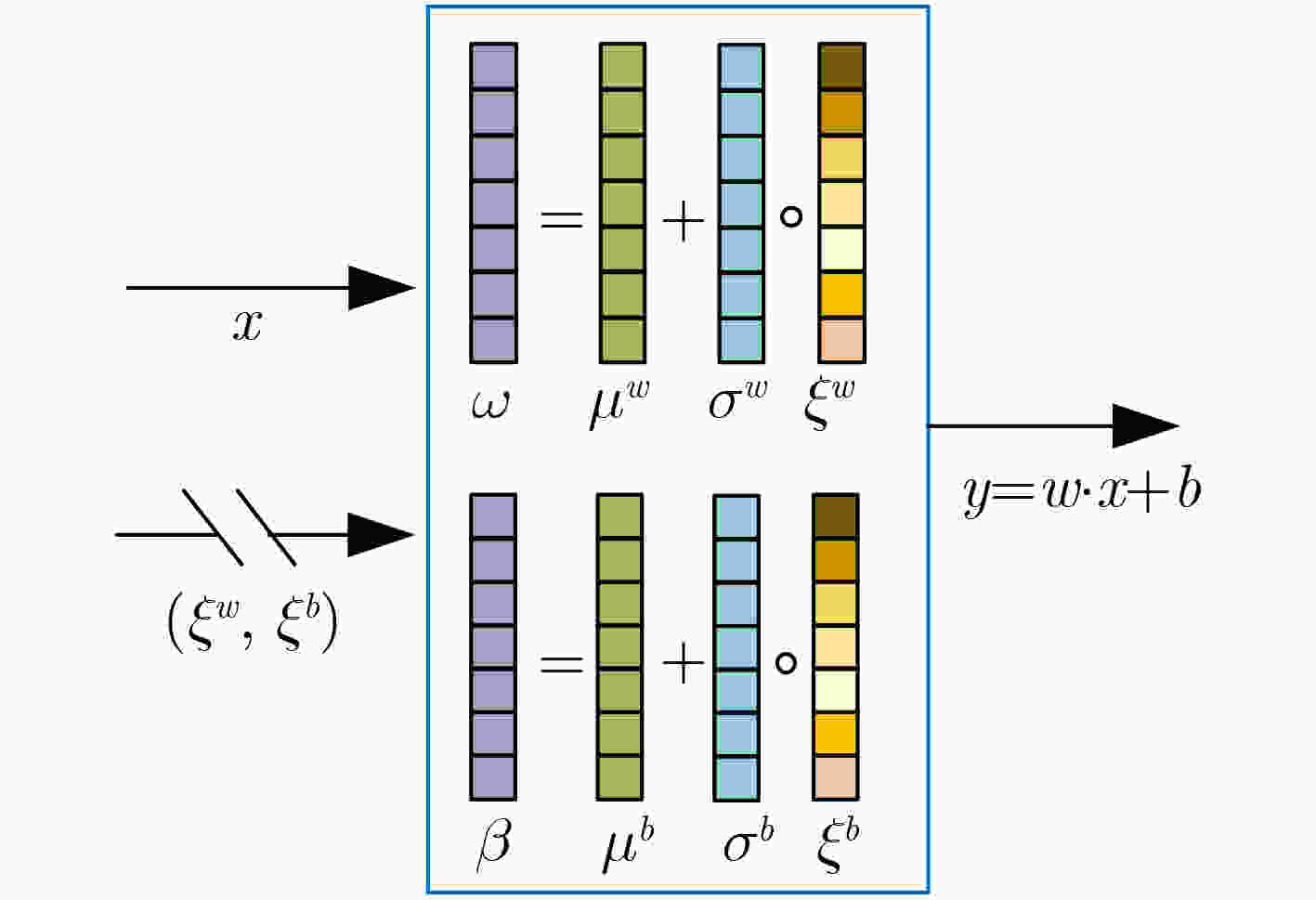
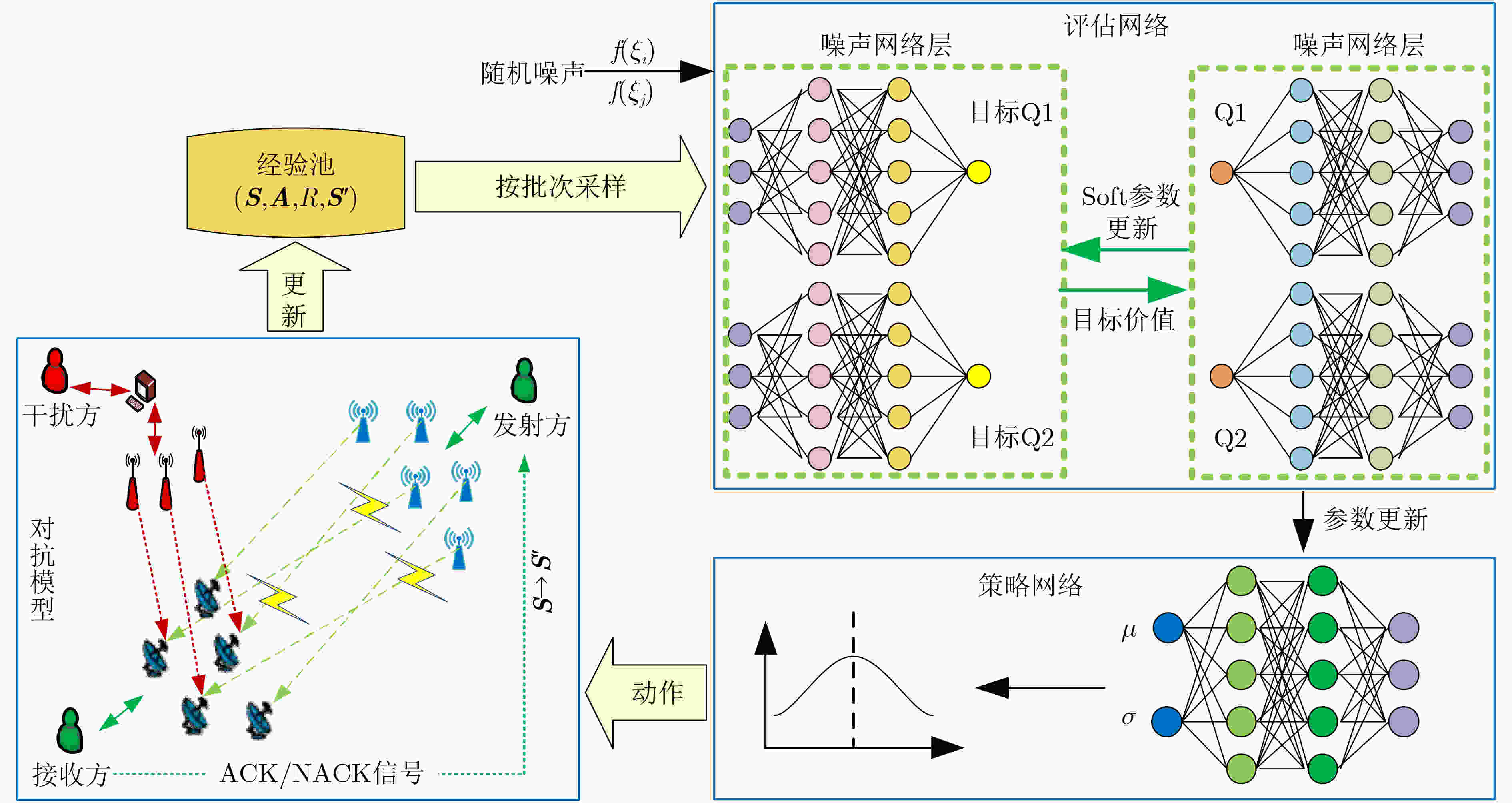
算法1 融合噪声网络的深度强化学习通信干扰资源分配算法 步骤1 随机初始化评估网络Noisy Q1和Noisy Q2,参数分别为$ {\theta _1} $和$ {\theta _2} $;($ \theta \triangleq \mu + \sigma \circ \xi $,$ \xi $为高斯噪声) 步骤2 随机初始化策略网络Policy Network,参数为$ \varphi $; 步骤3 初始化评估目标Noisy Q1网络和目标Noisy Q2网络,参数分别为$ {\bar \theta _1} \leftarrow {\theta _1},{\kern 1pt} {\bar \theta _2} \leftarrow {\theta _2} $; 步骤4 初始化经验回放池D; 步骤5 For episodes in 100 do: 初始化状态S0; For steps in 500 do: (1)根据状态选择动作$a$,执行动作$a$得到奖励值R和下一个状态${\boldsymbol{S}}'$ (2)存储$\left( {{\boldsymbol{S}},a,R,{\boldsymbol{S}}'} \right)$ 到回放池D当中,${\boldsymbol{S}} \leftarrow {\boldsymbol{S}}'$; If 回放池的当前容量> C: (a)从经验回放池中随机采样小批次样本$\left( {{S_i},{a_i},{R_i},{S_{i + 1}}} \right)$; (b)计算目标价值:$ {y_i} = R{}_i + \;\gamma \mathop {\min }\limits_{j = 1,2} {\bar Q_j}\left( {{S_{i + 1}},\bar a',{\xi _{i + 1}}|\bar \theta } \right) $; (c)最小化评估网络损失函数:$L\left( \theta \right) = {\kern 1pt} \dfrac{1}{B}{\displaystyle\sum\nolimits_i {\left( {R{}_i + \;\gamma \mathop {\min }\limits_{j = 1,2} {{\bar Q}_j}\left( {{S_{i + 1}},\bar a',{\xi _{i + 1}}|\bar \theta } \right) - Q\left( {{S_i},{a_i},{\xi _i}|\theta } \right)} \right)} ^2}$; 梯度下降更新评估网络参数$ {\theta _1} $和$ {\theta _2} $:$\theta \leftarrow \theta - {\alpha _\theta } \cdot {{\text{∇}} _\theta }L\left( \theta \right)\;$; (d)最小化策略网络损失函数:$ J\left( \varphi \right) = \dfrac{1}{B}{\displaystyle\sum\nolimits_i {\left( {\mathop {\min }\limits_{j = 1,2} {Q_j}\left( {{S_i},\bar a,{\xi _i}|\theta } \right) - \alpha \lg {\pi _\varphi }\left( {\bar a|{S_i}} \right)} \right)} ^2} $; 梯度下降更新策略网络参数$ \varphi $:$\varphi \leftarrow \varphi - {\alpha _\varphi } \cdot {{\text{∇}} _\varphi }J\left( \varphi \right)$; (e)单步更新目标Noisy Q1网络和目标Noisy Q2网络参数:$ {\bar \theta _1} \leftarrow \tau \; \cdot \;{\theta _1} + \left( {1 - \tau } \right){\bar \theta _1} $,$ {\bar \theta _2} \leftarrow \tau \; \cdot \;{\theta _2} + \left( {1 - \tau } \right){\bar \theta _2} $; End for End for 表 1 模型参数
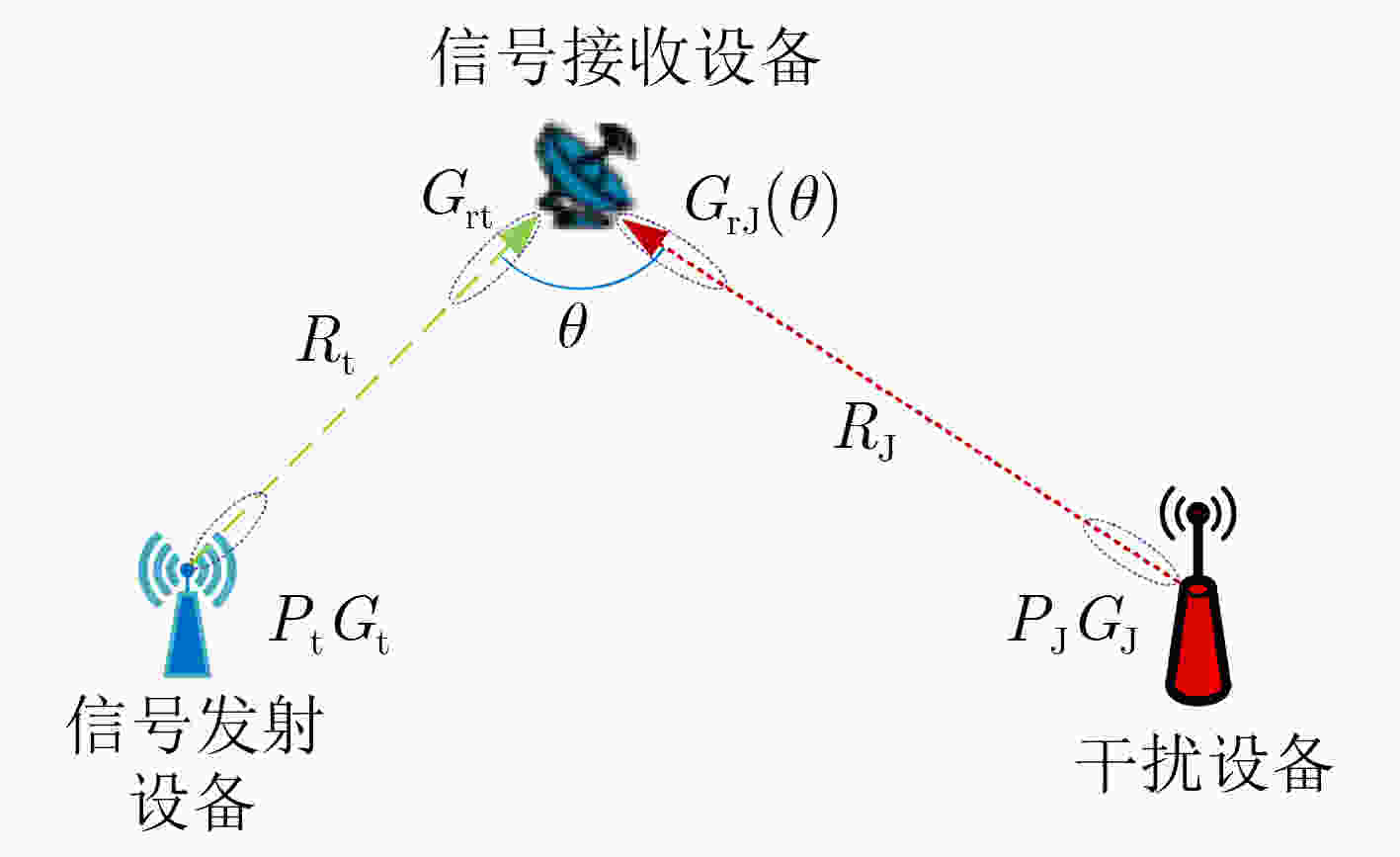
物理参数 值 通信链路天线增益${G_{\rm{t}}}$ 5 dB 干扰链路天线增益${G_{\rm{J}}}$ 8 dB 干扰设备最大干扰功率${P_{{\rm{J}}\max } }$ 90 dBm 通信信号发射功率${P_{\rm{t}}}$ 55 dBm 干扰信号传播距离${r_j}$ 300 km 中心频率$ f $ 225 MHz 符号错误率阈值$ \kappa $ 0.05 小批次样本大小B 256 经验回放池容量C 217 表 2 FNNDRL算法参数
参数 评估网络 策略网络 Noisy Q1,Q2 目标Noisy Q1,Q2 Policy Network 学习率 0.005 0.005 0.003 输入层 Linear,30(80) Linear,30(80) Linear,15(40) 隐藏层1 Noisy Linear,256,ReLU Noisy Linear, 256,ReLU Linear,256,ReLU 隐藏层2 Noisy Linear,256,ReLU Noisy Linear, 256,ReLU Linear,256,ReLU 输出层 Linear,1 Linear,1 30(80),Tanh 软更新系数$\tau $ Tau=0.01(0.001) Tau=0.01(0.001) —— Dropout概率 p=0.2 p=0.2 p=0.2 衰减系数 0.99 —— 表 3 DDPG算法参数
参数 Q网络 目标Q网络 策略网络 目标策略网络 学习率 0.001 0.001 输入层 Linear,30(80) Linear,30(80) Linear,15(40) Linear,15(40) 隐藏层 Linear,300(256),ReLU Linear,300(256),ReLU Linear,300(256),ReLU Linear,300(256),ReLU 输出层 Linear,1 Linear,1 15(40),Tanh 15(40),Tanh 软更新系数$\tau $ Tau=0.01 Tau=0.01 Tau=0.01 Tau=0.01 衰减系数 0.9 —— 表 4 A2C算法参数
参数 Critic网络 Actor网络 学习率 0.001 0.0001 输入层 Linear,15(40) Linear,15(40) 隐藏层 Linear,300(256),ReLU Linear, 300(256), ReLU 输出层 Linear,1 15(40),Tanh 衰减系数 0.99 -
[1] LIU Yafeng and DAI Yuhong. On the complexity of joint subcarrier and power allocation for multi-user OFDMA systems[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 583–596. doi: 10.1109/TSP.2013.2293130 [2] 宗思光, 刘涛, 梁善永. 基于改进遗传算法的干扰资源分配问题研究[J]. 电光与控制, 2018, 25(5): 41–45. doi: 10.3969/j.issn.1671-637X.2018.05.009ZONG Siguang, LIU Tao, and LIANG Shanyong. Interference resource allocation based on improved genetic algorithm[J]. Electro-Optics &Control, 2018, 25(5): 41–45. doi: 10.3969/j.issn.1671-637X.2018.05.009 [3] LUO Zhaoyi, DENG Min, YAO Zhiqiang, et al. Distributed blanket jamming resource scheduling for satellite navigation based on particle swarm optimization and genetic algorithm[C]. The IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 2020: 611–616. [4] XU Zhiwei and ZHANG Kai. Multiobjective multifactorial immune algorithm for multiobjective multitask optimization problems[J]. Applied Soft Computing, 2021, 107: 107399. doi: 10.1016/j.asoc.2021.107399 [5] TIAN Min, DENG Hongtao, and XU Mengying. Immune parallel artificial bee colony algorithm for spectrum allocation in cognitive radio sensor networks[C]. 2020 International Conference on Computer, Information and Telecommunication Systems (CITS), Hangzhou, China, 2020: 1–4. [6] 李东生, 高杨, 雍爱霞. 基于改进离散布谷鸟算法的干扰资源分配研究[J]. 电子与信息学报, 2016, 38(4): 899–905. doi: 10.11999/JEIT150726LI Dongsheng, GAO Yang, and YONG Aixia. Jamming resource allocation via improved discrete cuckoo search algorithm[J]. Journal of Electronics &Information Technology, 2016, 38(4): 899–905. doi: 10.11999/JEIT150726 [7] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing Atari with deep reinforcement learning[J]. arXiv: 1312.5602, 2013. [8] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236 [9] XIONG Xiong, ZHENG Kan, LEI Lei, et al. Resource allocation based on deep reinforcement learning in IoT edge computing[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(6): 1133–1146. doi: 10.1109/JSAC.2020.2986615 [10] HE Chaofan, HU Yang, CHEN Yan, et al. Joint power allocation and channel assignment for NOMA with deep reinforcement learning[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(10): 2200–2210. doi: 10.1109/JSAC.2019.2933762 [11] 黄星源, 李岩屹. 基于双Q学习算法的干扰资源分配策略[J]. 系统仿真学报, 2021, 33(8): 1801–1808. doi: 10.16182/j.issn1004731x.joss.20-0253HUANG Xingyuan and LI Yanyi. The allocation of jamming resources based on double Q-learning algorithm[J]. Journal of System Simulation, 2021, 33(8): 1801–1808. doi: 10.16182/j.issn1004731x.joss.20-0253 [12] 许华, 宋佰霖, 蒋磊, 等. 一种通信对抗干扰资源分配智能决策算法[J]. 电子与信息学报, 2021, 43(11): 3086–3095. doi: 10.11999/JEIT210115XU Hua, SONG Bailin, JIANG Lei, et al. An intelligent decision-making algorithm for communication countermeasure jamming resource allocation[J]. Journal of Electronics &Information Technology, 2021, 43(11): 3086–3095. doi: 10.11999/JEIT210115 [13] 饶宁, 许华, 齐子森, 等. 基于最大策略熵深度强化学习的通信干扰资源分配方法[J]. 西北工业大学学报, 2021, 39(5): 1077–1086. doi: 10.1051/jnwpu/20213951077RAO Ning, XU Hua, QI Zisen, et al. Allocation method of communication interference resource based on deep reinforcement learning of maximum policy entropy[J]. Journal of Northwestern Polytechnical University, 2021, 39(5): 1077–1086. doi: 10.1051/jnwpu/20213951077 [14] ZHONG Chen, WANG Feng, GURSOY M C, et al. Adversarial jamming attacks on deep reinforcement learning based dynamic multichannel access[C]. 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea (South), 2020: 1–6. [15] ZHONG Chen, LU Ziyang, GURSOY M C, et al. Actor-critic deep reinforcement learning for dynamic multichannel access[C]. 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, USA, 2018: 599–603. [16] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[C]. The 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016. [17] CUI Haoran, WANG Dongyu, LI Qi, et al. A2C deep reinforcement learning-based MEC network for offloading and resource allocation[C]. The 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 2021: 1905–1909. [18] XU Chen, WANG Jian, YU Tianhang, et al. Buffer-aware wireless scheduling based on deep reinforcement learning[C]. Proceedings of 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea (South), 2020: 1–6. [19] MENG Fan, CHEN Peng, WU Lenan, et al. Power allocation in multi-user cellular networks: Deep reinforcement learning approaches[J]. IEEE Transactions on Wireless Communications, 2020, 19(10): 6255–6267. doi: 10.1109/TWC.2020.3001736 [20] AMURU S, TEKIN C, VAN DER SCHAAR M, et al. Jamming bandits - a novel learning method for optimal jamming[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2792–2808. doi: 10.1109/TWC.2015.2510643 [21] FORTUNATO M, AZAR M G, PIOT B, et al. Noisy networks for exploration[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [22] KINGMA D P, SALIMANS T, and WELLING M. Variational dropout and the local reparameterization trick[C]. The 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2015: 2575–2583. [23] HAARNOJA T, TANG Haoran, ABBEEL P, et al. Reinforcement learning with deep energy-based policies[C]. The 34th International Conference on Machine Learning (ICML), Sydney, Australia, 2017: 1352–1361. [24] WANG Wenjing, BHATTACHARJEE S, CHATTERJEE M, et al. Collaborative jamming and collaborative defense in cognitive radio networks[J]. Pervasive and Mobile Computing, 2013, 9(4): 572–587. doi: 10.1016/j.pmcj.2012.06.008 -





 下载:
下载:


 下载:
下载:
