Resource Allocation Based on Weighted Bipartite Graph and Greedy Strategy for D2D Communication in Cellular Networks
-
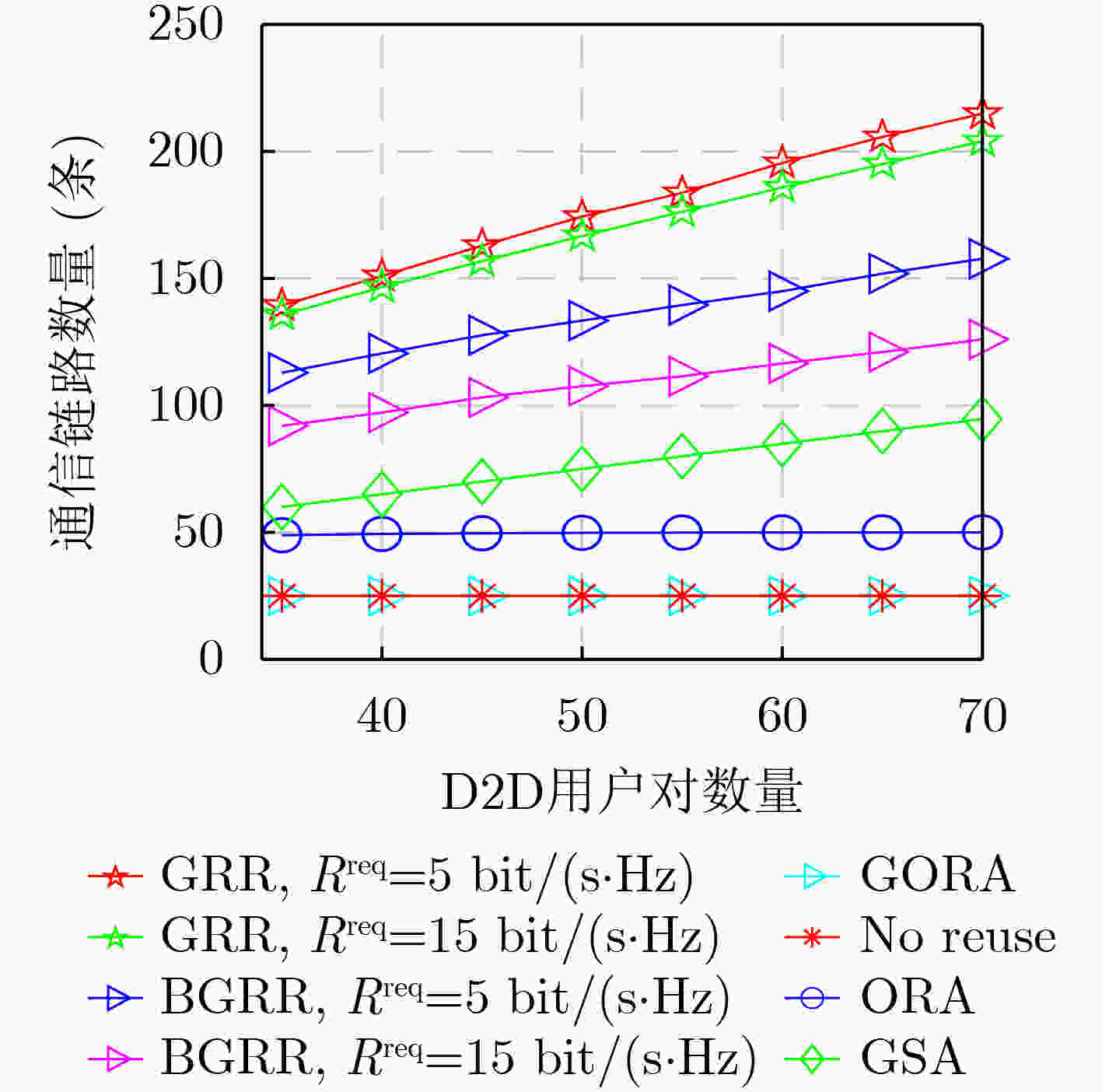
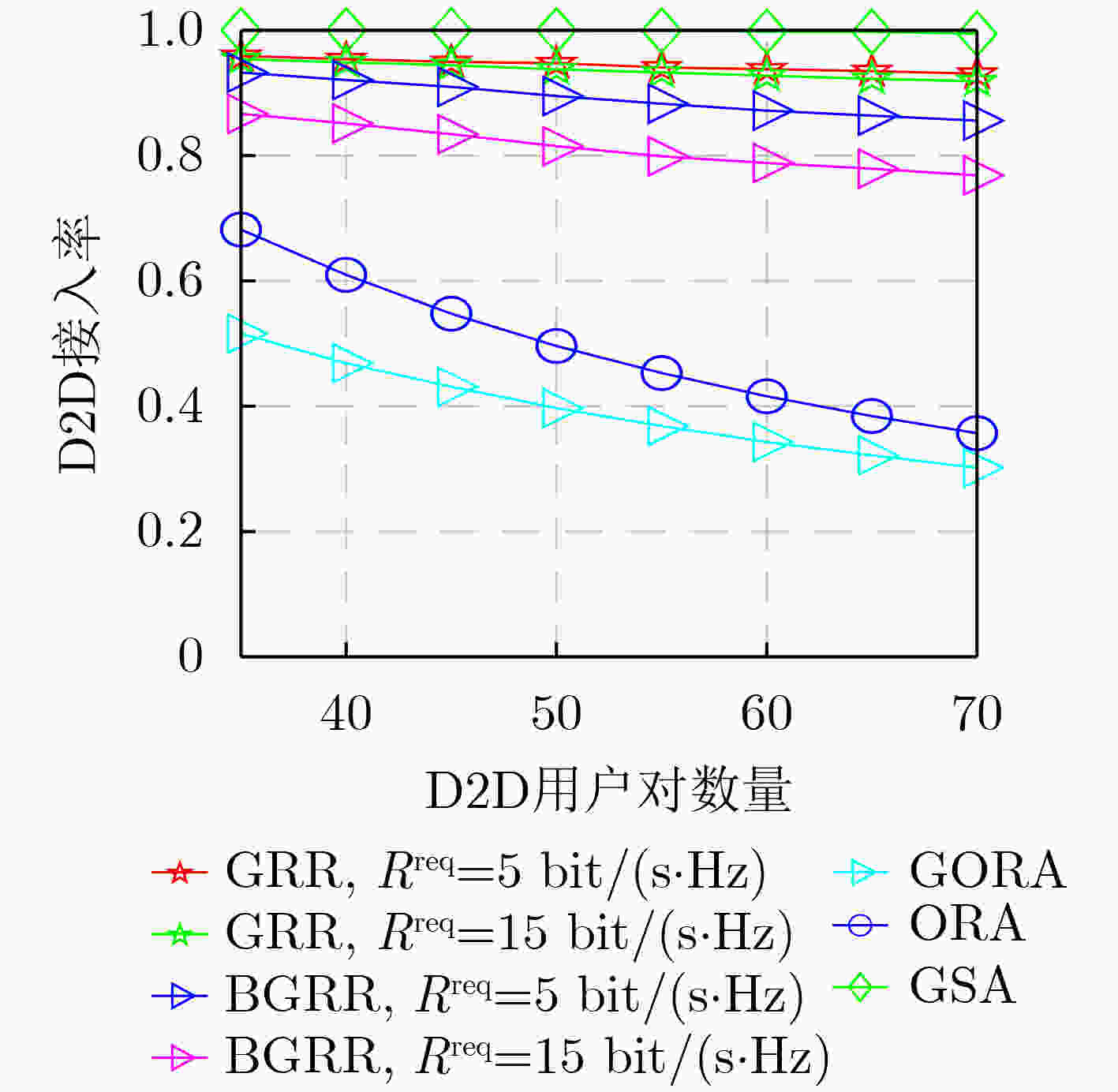
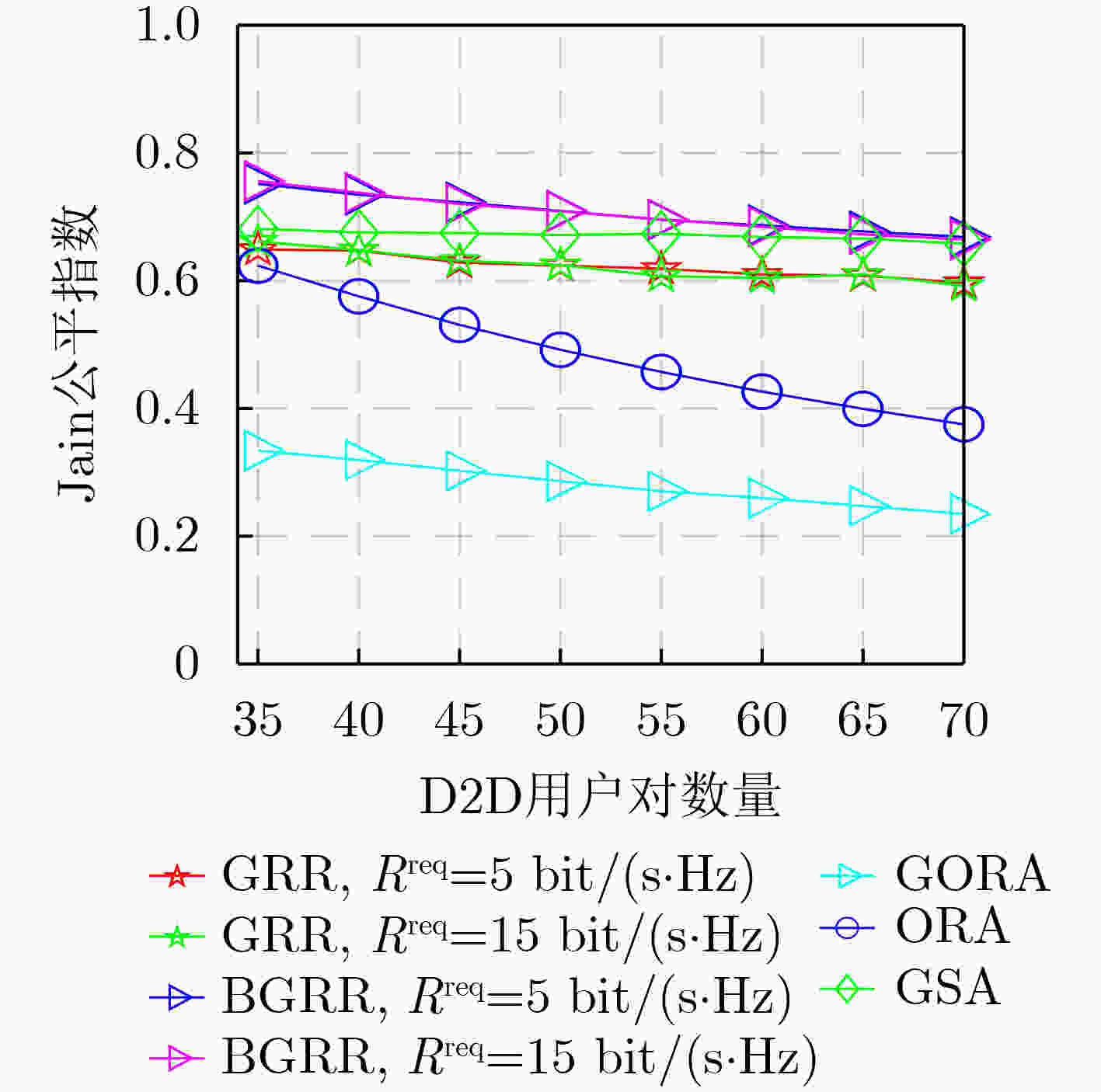
摘要: D2D(Device-to-Device)通信是解决频谱资源稀缺问题的关键技术之一。该文研究蜂窝网络中“many-to-many”的复杂场景,即单个RB(Resource Block)可以分配给多对D2D用户重用,并且允许单个D2D用户对使用多个RB,其中D2D用户对数量远多于蜂窝用户设备(Cellular User Equipment, CUE)数量和RB数量。考虑CUE对资源使用具有更高优先级,将此优化问题分解为蜂窝用户资源分配和D2D用户资源重用两个阶段。在第1阶段,提出基于公平性的循环二部图匹配(Fairness-based Circular Bipartite Graph Matching, FCBGM)算法,将现有的RB分配给所有CUE,以最大化蜂窝用户和速率。在第2阶段,分别提出基于二部图的资源重用(Bipartite Graph-based Resource Reuse, BGRR)算法和基于贪婪策略的资源重用(Greedy-based Resource Reuse, GRR)算法,目标是将已经分配给CUE的RB再次分配给D2D用户重用,以最大化系统和速率,同时确保CUE的基本速率需求。仿真结果表明,在D2D用户对数量远大于CUE数量和RB数量的情况下,与现有典型算法相比,所提算法能够有效提高系统和速率,增加D2D接入率,同时兼顾用户公平性和服务质量需求。Abstract: Device-to-Device (D2D) communication is one of the key technologies to solve the issue of spectrum resource scarcity. In this paper, a complex “many-to-many” scenario in cellular networks is investigated, where a Resource Block (RB) could be reused by more than one D2D pair, and a D2D pair is also allowed to use multiple RBs. Moreover, the number of D2D users is larger than that of Cellular User Equipments (CUEs) and RBs. Considering that CUEs have higher priority on resource, this optimization problem is decomposed into two stages: cellular users resource allocation and D2D user resource reuse. In the first stage, a Fairness-based Circular Bipartite Graph Matching (FCBGM) algorithm is proposed, which allocates the existing RBs to all CUEs to maximize the sum data rate of cellular users. In the second stage, a Bipartite Graph-based Resource Reuse (BGRR) algorithm and a Greedy-based Resource Reuse (GRR) algorithm is proposed, and the goal is to re-assign the RBs, which are already allocated to CUEs, to the D2D pairs in a way to maximize the system sum data rate while ensuring the basic data rate requirements of CUEs. Simulation results show that when the number of D2D pairs is much larger than that of CUEs and RBs, compared with the existing typical algorithms, the proposed algorithm can effectively improve system sum data rate and D2D access rate while guaranteeing user fairness and quality of service.
-
表 1 本文所提算法与现有典型算法的比较
表 2 信道增益
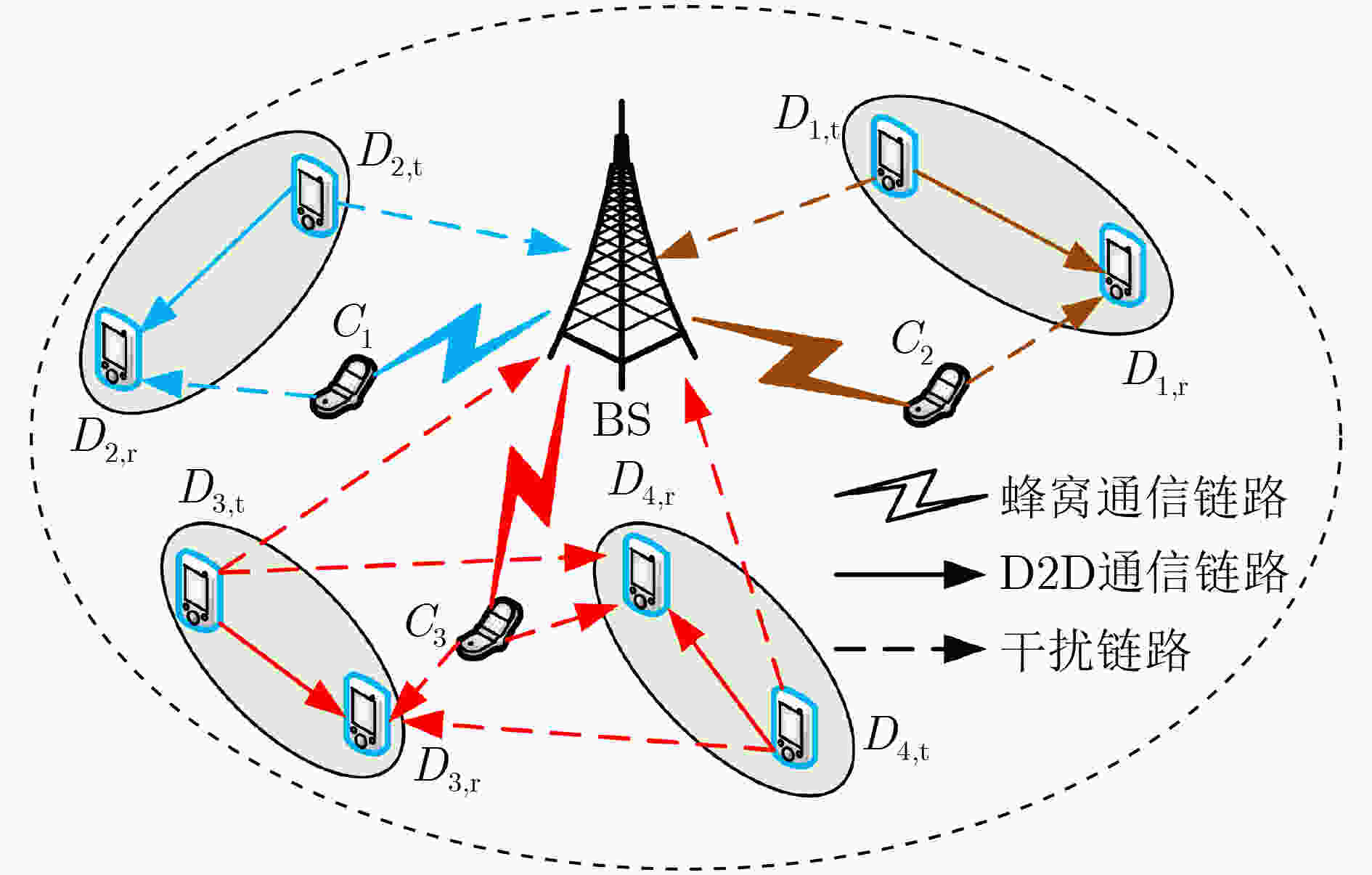
${\text{R}}{{\text{B}}_k}$信道增益 ${\text{A}}{\mkern 1mu} {\mkern 1mu} \Rightarrow {\mkern 1mu} {\mkern 1mu} {\text{B}}{\mkern 1mu} {\mkern 1mu} $(${\text{from A to B}}$) $g_{m,{\text{B}}}^k$ 蜂窝通信链路${C_m} \Rightarrow {\text{BS}}{\mkern 1mu} {\mkern 1mu} $ $g_{n,{\text{t}},n,{\text{r}}}^k$ D2D通信链路${D_{n,{\text{t}}}} \Rightarrow {D_{n,{\text{r}}}}$ $g_{n,{\text{t}},{\text{B}}}^k$ 干扰链路${D_{n,{\text{t}}}} \Rightarrow {\text{BS}}{\mkern 1mu} {\mkern 1mu} $ $g^k_{m,n,{\text{r} } }$ 干扰链路${C_m} \Rightarrow {D_{n,{\text{r}}}}$ $g_{_{n,{\text{t,}}n',{\text{r}}}}^k$ 干扰链路${D_{n,{\text{t}}}} \Rightarrow {D_{n',{\text{r}}}}$ 算法1 基于公平性的循环二部图匹配算法 输入:$\mathcal{C},\mathcal{R}$ 输出:${{\boldsymbol{A}}_{\text{C}}}$ 1:初始化 ${{\boldsymbol{A}}_{\text{C}}} = {[\alpha _m^k]_{M \times K}}$,$\alpha _m^k = 0$,$\forall m \in \mathcal{M},\forall k \in \mathcal{K}$,${\mathcal{R}_1} = \mathcal{R}$ 2:While ${\mathcal{R}_1} \ne \varnothing $ do 3:根据$\mathcal{C}$和${\mathcal{R}_1}$构造加权完全二部图${\boldsymbol{G}} = \left( {{{\boldsymbol{V}}_1},{{\boldsymbol{V}}_2},{\boldsymbol{E}},{\boldsymbol{W}}} \right)$ 4:添加虚拟顶点,使得$\left| {{{\boldsymbol{V}}_1}} \right| = \left| {{{\boldsymbol{V}}_2}} \right| = L$ 5:根据式(14)计算${{\boldsymbol{W}}_1}$ 6:通过KM算法求解问题式(15)获得${{\boldsymbol{M}}_0}$ 7:获得匹配${{\boldsymbol{M}}^*} \leftarrow {{\boldsymbol{M}}_0} \setminus {{\boldsymbol{E}}_{{\text{virtual}}}}$ 8:更新${{\boldsymbol{A}}_{\text{C}}}$ for each${e_{m,k}} \in {{\boldsymbol{M}}^*}$do $\alpha _m^k = 1$,${\mathcal{R}_1} \leftarrow {\mathcal{R}_1} \setminus {\text{ R}}{{\text{B}}_k}$ end for 9: end While 算法2 基于二部图的资源重用算法 输入:$\mathcal{C},\mathcal{R},\mathcal{D}$ 输出:${{\boldsymbol{A}}_{\text{C}}},{{\boldsymbol{A}}_{\text{D}}}$ 1:初始化 $\beta _n^k = 0$,${R_{n,k}} = 0$,${R'_{m,k,n}} = 0$,${f_{n,k}} = 1$,$\Delta {R_{n,k}} = 0$,
$\forall n \in \mathcal{N},\forall k \in \mathcal{K},\forall m \in \mathcal{M}$2:根据FCBGM算法求得${{\boldsymbol{A}}_{\text{C}}}$,根据式(22)计算${\boldsymbol{R}}_{{\text{C}},{\text{RB}}}^{{\text{req}}}$ 3:While${\boldsymbol{f}} \ne {\boldsymbol{0}}$do 4:根据$\mathcal{D},\mathcal{R}$构造加权二部图${\boldsymbol{G'}} = ({{\boldsymbol{V'}}_1},{{\boldsymbol{V'}}_2},{\boldsymbol{E'}},{\boldsymbol{W'}})$ 5:添加虚拟顶点使得$\left| {{{{\boldsymbol{V'}}}_1}} \right| = \left| {{{{\boldsymbol{V'}}}_2}} \right| = L'$ 6:令${f_{n,k}} = 0$$\forall n,k \in \left\{ {1,2, \cdots ,L'} \right\}$ 7:根据式(23)计算权重矩阵${{\boldsymbol{W'}}_1}$并更新${\boldsymbol{f}}$ 8:if${f_{n,k}} = 0$,$\forall n,k \in \left\{ {1,2, \cdots ,L'} \right\}$then break else 9: 把${{\boldsymbol{W'}}_1}$作为KM算法的输入,获得最大权完美匹配${{\boldsymbol{M'}}_0}$ 10: 删除${{\boldsymbol{M'}}_0}$中与虚拟顶点关联的边,得到匹配${\boldsymbol{M}}_1^*$ 11: 根据重用标准(1)和标准(2)更新${{\boldsymbol{A}}_{\text{D}}}$ 12:end While 算法3 基于贪婪策略的资源重用算法 输入:$\mathcal{C},\mathcal{R},\mathcal{D}$ 输出:${{\boldsymbol{A}}_{\text{C}}},{{\boldsymbol{A}}_{\text{D}}}$ 1:初始化 $\beta _n^k = 0$,${R_{m,k}} = 0$,$\forall n \in \mathcal{N},\forall k \in \mathcal{K},\forall m \in \mathcal{M}$ 2:根据FCBGM算法求得${{\boldsymbol{A}}_{\text{C}}}$,根据式(16)更新${{\boldsymbol{R}}_{\text{C}}}$ 3:假设D2D用户重用RB,根据式(17)、式(18)、式(19)、
式(20)分别计算${R_{n,k}}$,${R'_{m,k,n}}$,$\Delta {R'_{n,k}}$,$\Delta {R_{n,k}}$4:找出$\Delta {\boldsymbol{R}}$中最大值对应的D2D和RB以及与该RB关联的CUE $\left( {n*,k*} \right) = \arg \max \Delta {R_{n,k}},\forall n \in \mathcal{N},\forall k \in \mathcal{K}$ $m* = \{ m:\alpha _m^{k*} = 1,\forall m \in \mathcal{M}\} $ 5:计算${C_{m*}}$的传输速率
${R_{m*}} = {R'_{m*,k*,n*}} + \displaystyle\sum\nolimits_{k' = 1,k' \ne k*}^K {{R_{m*,k'}}} $6:判断${D_{n*}}$重用${\text{R}}{{\text{B}}_{k*}}$是否满足重用标准来决定资源重用结果 if $\Delta {R_{n*,k*}} \ge 0$ and ${R_{m*}} \ge R_{m*}^{{\text{req}}}$ then $\beta _{n*}^{k*} = 1$ and ${R_{m*,k*}} = {R'_{m*,k*,n*}}$ 转到步骤3 else if $\Delta {R_{n*,k*}} \ge 0$ and ${R_{m*}} < R_{m*}^{{\text{req}}}$ then $\Delta {R_{n*,k*}} = - {\text{ }}\infty $ 转到步骤4 end if 表 3 主要仿真参数
参数 数值 蜂窝层 单小区 蜂窝半径 500 m RB数量$K$ 25 CUE数量$M$ 10 D2D用户对数量$N$ 35~70 CUE的最大发射功率$P_m^{{\text{max}}}$ 24 dBm D2D用户对的最大发射功率$P_n^{{\text{max}}}$ 24 dBm CUE的最小速率需求$R_m^{{\text{req}}}$ 5 bit/(s·Hz)和15 bit/(s·Hz) 路径损耗常数$G$ 10–2 路径损耗指数$\gamma $ 3 大尺度衰落增益$F$ 标准差为8 dB的对数正态阴影 小尺度衰落增益$h$ 均值为1的指数分布 D2D用户对的收发距离 50 m 噪声功率谱密度 –174 dBm/Hz -
[1] WEI Lili, HU R Q, QIAN Yi, et al. Enable device-to-device communications underlaying cellular networks: Challenges and research aspects[J]. IEEE Communications Magazine, 2014, 52(6): 90–96. doi: 10.1109/MCOM.2014.6829950 [2] CAO Jin, MA Maode, LI Hui, et al. A survey on security aspects for 3GPP 5G networks[J]. IEEE Communications Surveys & Tutorials, 2020, 22(1): 170–195. doi: 10.1109/COMST.2019.2951818 [3] LIANG Le, XIE Shijie, LI G Y, et al. Graph-based resource sharing in vehicular communication[J]. IEEE Transactions on Wireless Communications, 2018, 17(7): 4579–4592. doi: 10.1109/TWC.2018.2827958 [4] 易鑫, 裴二荣. D2D辅助NB-IoT系统的传输设备数优化算法[J]. 重庆邮电大学学报:自然科学版, 2021, 33(4): 606–613. doi: 10.3979/j.issn.1673-825X.201910310378YI Xin and PEI Errong. Transmission device number optimization algorithm for D2D-assisted NB-IoT system[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2021, 33(4): 606–613. doi: 10.3979/j.issn.1673-825X.201910310378 [5] AHMED M, LI Yong, WAQAS M, et al. A survey on socially aware device-to-device communications[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2169–2197. doi: 10.1109/COMST.2018.2820069 [6] WAQAS M, NIU Yong, LI Yong, et al. A comprehensive survey on mobility-aware D2D communications: Principles, practice and challenges[J]. IEEE Communications Surveys & Tutorials, 2020, 22(3): 1863–1886. doi: 10.1109/COMST.2019.2923708 [7] ZHANG Shangwei, LIU Jiajia, GUO Hongzhi, et al. Envisioning device-to-device communications in 6G[J]. IEEE Network, 2020, 34(3): 86–91. doi: 10.1109/MNET.001.1900652 [8] FENG Daquan, LU Lu, YUAN-WU Y, et al. Device-to-device communications underlaying cellular networks[J]. IEEE Transactions on Communications, 2013, 61(8): 3541–3551. doi: 10.1109/TCOMM.2013.071013.120787 [9] ZHAO Wentao and WANG Shaowei. Resource sharing scheme for device-to-device communication underlaying cellular networks[J]. IEEE Transactions on Communications, 2015, 63(12): 4838–4848. doi: 10.1109/TCOMM.2015.2495217 [10] HAMDOUN S, RACHEDI A, and GHAMRI-DOUDANE Y. Radio resource sharing for MTC in LTE-A: An interference-aware bipartite graph approach[C]. 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, USA, 2015: 1–7. [11] KÖSE A and ÖZBEK B. Resource allocation for underlaying device-to-device communications using maximal independent sets and knapsack algorithm[C]. 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, 2018: 1–5. [12] CAI Xuejia, ZHENG Jun, and ZHANG Yuan. A Graph-coloring based resource allocation algorithm for D2D communication in cellular networks[C]. 2015 IEEE International Conference on Communications (ICC), London, UK, 2015: 5429–5434. [13] ZHANG Rongqing, CHENG Xiang, YANG Liuqing, et al. Interference Graph-based resource allocation (InGRA) for D2D communications underlaying cellular networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(8): 3844–3850. doi: 10.1109/TVT.2014.2356198 [14] KAI Caihong, LI Hui, XU Lei, et al. Joint subcarrier assignment with power allocation for sum rate maximization of D2D communications in wireless cellular networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4748–4759. doi: 10.1109/TVT.2019.2903815 [15] LAI Weikuang, WANG Y C, LIN H C, et al. Efficient resource allocation and power control for LTE-A D2D communication with pure D2D model[J]. IEEE Transactions on Vehicular Technology, 2020, 69(3): 3202–3216. doi: 10.1109/TVT.2020.2964286 [16] ABANTO-LEON L F, KOPPELAAR A, and DE GROOT S H. Graph-based resource allocation with conflict avoidance for V2V broadcast communications[C]. 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, Canada, 2017: 1–7. [17] LI Y B, DONG G, and LIU D D. An improved multi-cell resource allocation scheme based on graph theory[C]. 2015 International Conference on Information and Communications Technologies (ICT 2015), Xi'an, China, 2015: 1–6. [18] FERDOUSE L, WOUNGANG I, ANPALAGAN A, et al. Energy efficient downlink resource allocation in cellular iot supported H-CRANs[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 5803–5816. doi: 10.1109/TVT.2021.3076825 -





 下载:
下载:


 下载:
下载:
