II型Z-优化二元互补序列对的构造

林金朝; 周银萍; 李国军; 叶昌荣; 曾凡鑫

doi:10.11999/JEIT220014

II型Z-优化二元互补序列对的构造

doi: 10.11999/JEIT220014

林金朝²,
周银萍^{1, 2, ,},
李国军²,
叶昌荣²,
曾凡鑫²

1.
重庆邮电大学通信与信息工程学院重庆 400065
2.
重庆邮电大学超视距可信信息传输研究所重庆 400065

基金项目: 国家重点研发计划(2019YFC1511300)，重庆市基础研究与前沿探索项目(cstc2021ycjh-bgzxm0072)

详细信息

作者简介:
林金朝：男，教授，研究方向为无线通信传输技术、BAN网络与信息处理技术

周银萍：女，硕士生，研究方向为序列设计、信号处理

李国军：男，教授，研究方向为军民融合应急指挥信息系统体质标准、核心技术、关键装备与规划建设

叶昌荣：男，副教授，研究方向为短波通信、信号处理

曾凡鑫：男，教授，研究方向为序列设计、纠错码、信号处理

通讯作者:
周银萍　s190101006@stu.cqupt.edu.cn

中图分类号: TN911.2
计量
- 文章访问数: 543
- HTML全文浏览量: 441
- PDF下载量: 77
- 被引次数: 0
出版历程
- 收稿日期: 2022-01-06
- 修回日期: 2022-05-19
- 网络出版日期: 2022-05-24
- 刊出日期: 2023-03-10

Construction of Type II Z-Optimal Binary Complementary Sequence Pairs

1.
School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
Laboratory of Beyond Line of Sight Reliable Information Transmission, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

Funds: The National Key Research and Development Program of China (2019YFC1511300), Chongqing Basic Research and Frontier Exploration Project (cstc2021ycjh-bgzxm0072)

摘要

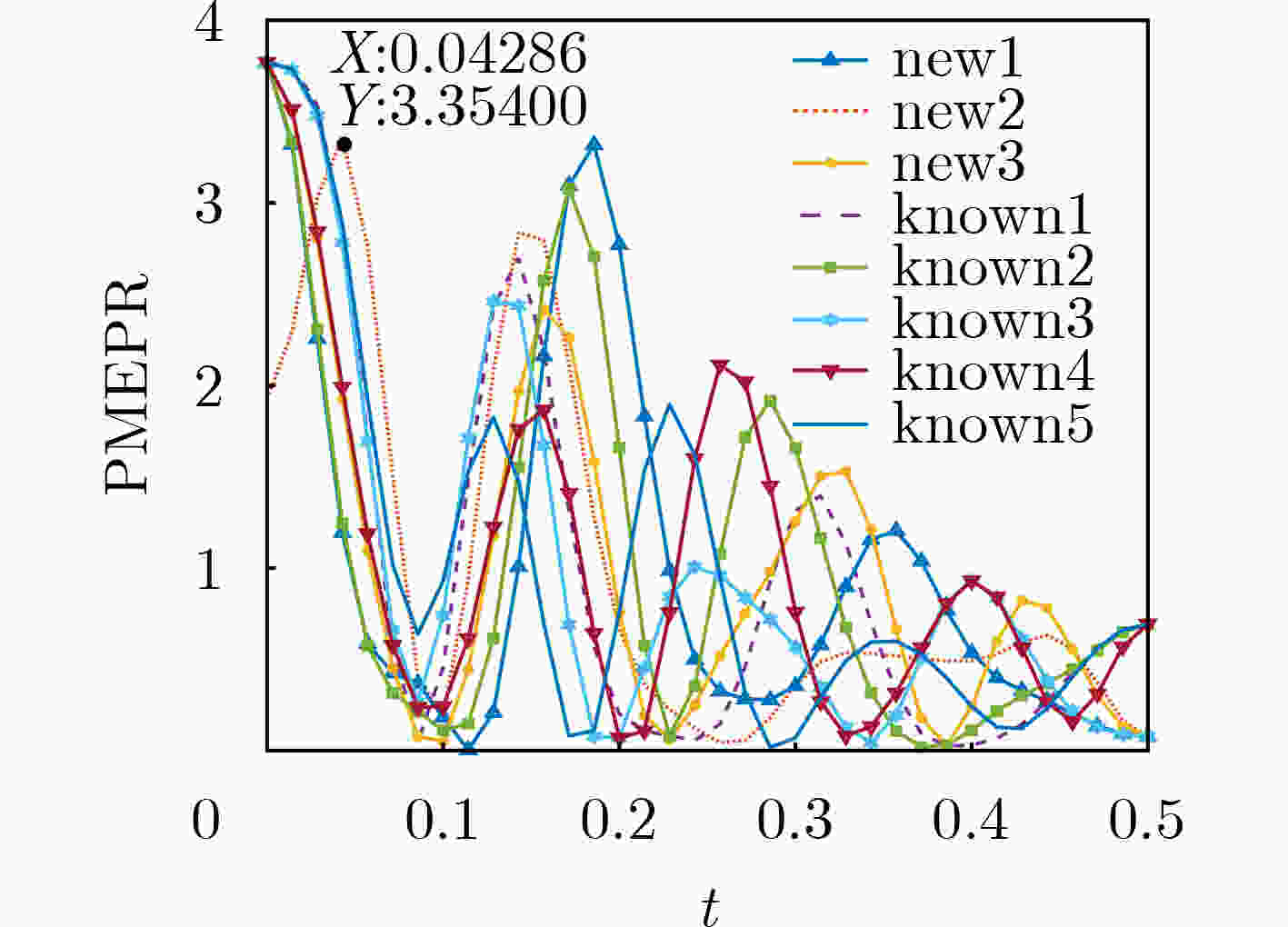
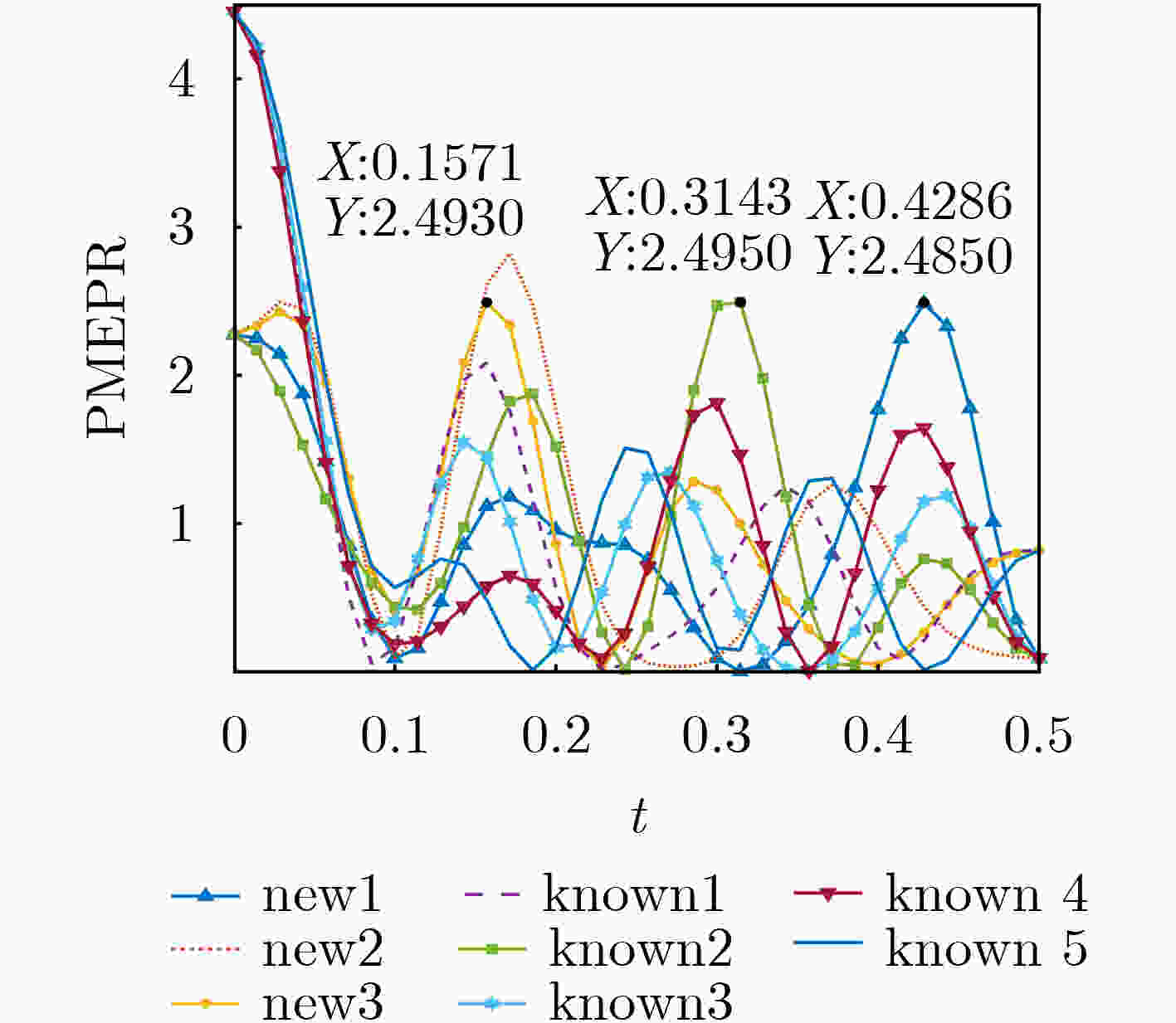
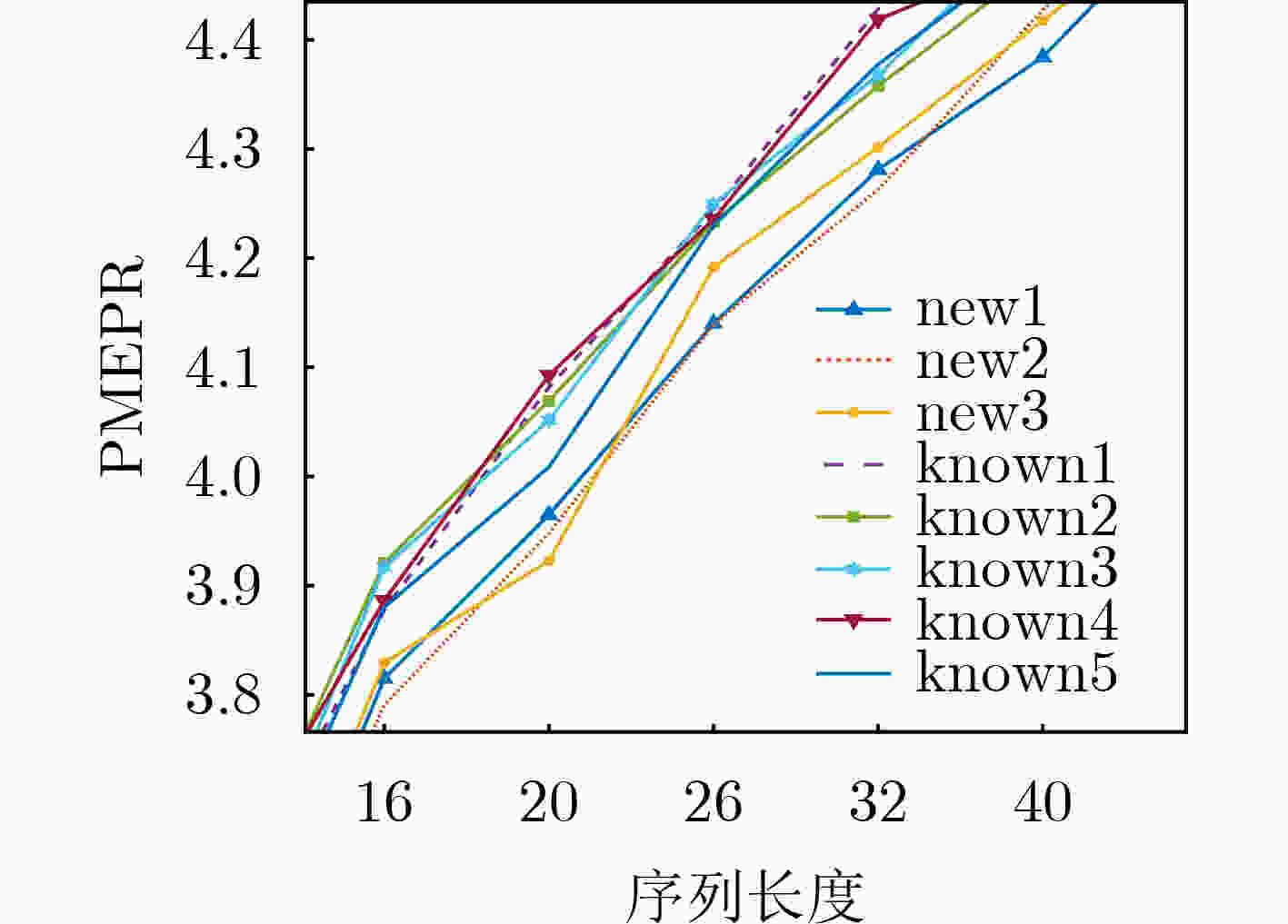
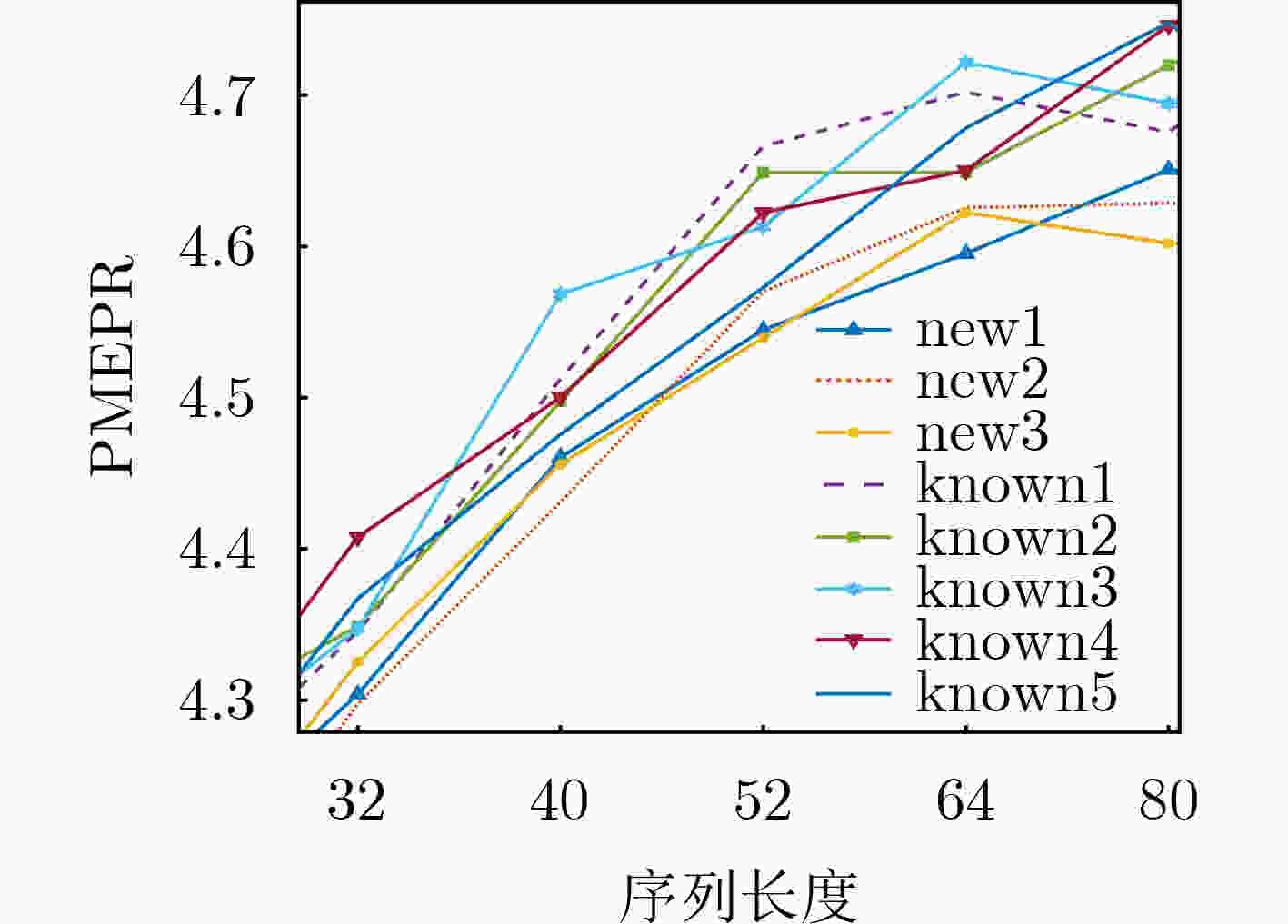
摘要: 该文以长度为N(N为整数)的Golay互补对(GCP)为种子序列对，在种子序列对的3个选定位置中插入特定的码元，构造出长度为N+3的II型Z-优化2元Z-互补序列对(ZCP)。与已知同长度II型Z-优化2元Z-互补序列对相比，构造的新序列有更低的峰均包络功率比(PMEPR)。Z-互补序列对和Golay互补序列对都广泛应用于正交频分复用(OFDM)系统和码分多址(CDMA)系统等，但前者有更灵活的序列长度和更多的序列数量，更能满足应用的需求。
- 序列设计 /
- Z-互补对 /
- Golay互补对 /
- Z-优化 /
- 峰均包络功率比
Abstract: Based on a length-N Golay Complementary sequence Pair (GCP) as a seed, a Z-optimal binary Z-Complementary sequence Pair (ZCP) with length N+3 is constructed by inserting three specific components at chosen positions in the aforementioned seed, where N is an integer. Compared with the known Type-II Z-optimal binary ZCPs of the same length, the resultant pairs have lower Peak-to-Mean Envelope Power Ratio (PMEPR). Both ZCPs and GCPs are widely used in Orthogonal Frequency Division Multiplexing (OFDM) systems and Code Division Multiple Access (CDMA) system, etc, however, the former has more flexible lengths and larger family sizes, which can better meet the requirements of applications.
- Sequence design /
- Z-Complementary Pairs (ZCPs) /
- Golay Complementary Pairs (GCPs) /
- Z-optimal /
- Peak -to-Mean Envelope Power Ratio (PMEPR)

HTML全文

图 1 I型条件下序列长度为13的8种插入方法的PMEPR对比

下载: 全尺寸图片幻灯片

图 2 II型条件下序列长度为11的8种插入方法的PMEPR对比

下载: 全尺寸图片幻灯片

图 3 I型条件下不同长度序列的PMEPR

下载: 全尺寸图片幻灯片

图 4 II型条件下不同长度序列的PMEPR

下载: 全尺寸图片幻灯片

表 1 I型及II型构造条件

例	$ (w,v) $	I型条件	II型条件
new1	$ \begin{gathered} (({i_1})\|\|{a_1}\|\|{a_2}\|\|({i_2},{i_3})) \\ (({j_1})\|\|{b_1}\|\|{b_2}\|\|({j_2},{j_3})) \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = {j_1}; \\ {i_2} = - {j_2};{i_3} = - {j_3} \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = - {j_1}; \\ {i_2} = {j_2};{i_3} = {j_3} \\ \end{gathered} $
new2	$ \begin{gathered} (({i_1},{i_2})\|\|{a_1}\|\|{a_2}\|\|({i_3})) \\ (({j_1},{j_2})\|\|{b_1}\|\|{b_2}\|\|({j_3})) \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = {j_1}; \\ {i_2} = {j_2};{i_3} = - {j_3} \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = - {j_1}; \\ {i_2} = - {j_2};{i_3} = {j_3} \\ \end{gathered} $
new3	$ \begin{gathered} (({i_1})\|\|{a_1}\|\|({i_2})\|\|{a_2}\|\|({i_3})) \\ (({j_1})\|\|{b_1}\|\|({j_2})\|\|{b_2}\|\|({j_3})) \\ \end{gathered} $	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ; \\ {i_1} = {j_1};{i_3} = - {j_3} \\ \end{gathered}$	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ; \\ {i_1} = - {j_1};{i_3} = {j_3} \\ \end{gathered}$
known1^[20]	$ \begin{gathered} (({i_1},{i_2})\|\|{a_1}\|\|({i_3})\|\|{a_2}) \\ (({j_1},{j_2})\|\|{b_1}\|\|({j_3})\|\|{b_2}) \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} {\text{ ;}}{i_1} = {j_1}; \\ {i_2} = {j_2};{i_3} = - {j_3} \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = - {j_1}; \\ {i_2} = - {j_2};{i_3} = {j_3} \\ \end{gathered} $
know2^[20]	$ \begin{gathered} ({a_1}\|\|({i_1})\|\|{a_2}\|\|({i_2},{i_3})) \\ ({b_1}\|\|({j_1})\|\|{b_2}\|\|({j_2},{j_3})) \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = {j_1}; \\ {i_2} = - {j_2};{i_3} = - {j_3} \\ \end{gathered} $	$ \begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ;{i_1} = 1 - {j_1}; \\ {i_2} = {j_2};{i_3} = {j_3} \\ \end{gathered} $
known3^[20]	$ \begin{gathered} (({i_1})\|\|{a_1}\|\|({i_2},{i_3})\|\|{a_2}) \\ (({j_1})\|\|{b_1}\|\|({j_2},{j_3})\|\|{b_2}) \\ \end{gathered} $	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\}; \\ {i_1} = {j_1};{i_3} = - {j_3} \\ \end{gathered}$	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ; \\ {i_1} = - {j_1};{i_3} = {j_3} \\ \end{gathered}$
known4^[20]	$ \begin{gathered} ({a_1}\|\|({i_1},{i_2})\|\|{a_2}\|\|({i_3})) \\ ({b_1}\|\|({j_1},{j_2})\|\|{b_2}\|\|({j_3})) \\ \end{gathered} $	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\}; \\ {i_1} = {j_1};{i_3} = - {j_3} \\ \end{gathered}$	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ; \\ {i_1} = - {j_1};{i_3} = {j_3} \\ \end{gathered}$
known5^[20]	$ \begin{gathered} ({a_1}\|\|({i_1},{i_2},{i_3})\|\|{a_2}) \\ ({b_1}\|\|({j_1},{j_2},{j_3})\|\|{b_2}) \\ \end{gathered} $	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\}; \\ {i_1} = {j_1};{i_3} = - {j_3} \\ \end{gathered}$	$\begin{gathered} {i_k},{j_k} \in \{ \pm 1\} ; \\ {i_1} = - {j_1};{i_3} = {j_3} \\ \end{gathered}$

下载: 导出CSV

参考文献(21)

[1]	GOLAY M. Complementary series[J]. IRE Transactions on Information Theory, 1961, 7(2): 82–87. doi: 10.1109/TIT.1961.1057620
[2]	WELTI G. Quaternary codes for pulsed radar[J]. IRE Transactions on Information Theory, 1960, 6(3): 400–408. doi: 10.1109/TIT.1960.1057572
[3]	SPASOJEVIC P and GEORGHIADES C N. Complementary sequences for ISI channel estimation[J]. IEEE Transactions on Information Theory, 2001, 47(3): 1145–1152. doi: 10.1109/18.915670
[4]	POPOVIC B M. Synthesis of power efficient multitone signals with flat amplitude spectrum[J]. IEEE Transactions on Communications, 1991, 39(7): 1031–1033. doi: 10.1109/26.87205
[5]	DAVIS J A and JEDWAB J. Peak-to-mean power control in OFDM, Golay complementary sequences and Reed-Muller codes[J]. IEEE Transactions on Information Theory, 1999, 45(7): 2397–2417. doi: 10.1109/18.796380
[6]	TSENG C C and LIU C. Complementary sets of sequences[J]. IEEE Transactions on Information Theory, 1972, 18(5): 644–652. doi: 10.1109/TIT.1972.1054860
[7]	APARICIO J and SHIMURA T. Asynchronous detection and identification of multiple users by multi-carrier modulated complementary set of sequences[J]. IEEE Access, 2018, 6: 22054–22069. doi: 10.1109/ACCESS.2018.2828500
[8]	FAN Pingzhi, YUAN Weina, and TU Yifeng. Z-complementary binary sequences[J]. IEEE Signal Processing Letters, 2007, 14(8): 509–512. doi: 10.1109/LSP.2007.891834
[9]	陈晓玉, 高茜超, 李永杰. 最佳零相关区序列集构造法[J]. 通信学报, 2020, 41(8): 215–222. doi: 10.11959/j.issn.1000-436x.2020175 CHEN Xiaoyu, GAO Xichao, and LI Yongjie. Construction of optimal zero correlation zone sequence set[J]. Journal on Communications, 2020, 41(8): 215–222. doi: 10.11959/j.issn.1000-436x.2020175
[10]	ADHIKARY A R, MAJHI S, LIU Zilong, et al. New sets of optimal odd-length binary Z-complementary pairs[J]. IEEE Transactions on Information Theory, 2020, 66(1): 669–678. doi: 10.1109/TIT.2019.2944185
[11]	LIU Zilong, PARAMPALLI U, and GUAN Yongliang. Optimal odd-length binary Z-complementary pairs[J]. IEEE Transactions on Information Theory, 2014, 60(9): 5768–5781. doi: 10.1109/TIT.2014.2335731
[12]	ADHIKARY A R, MAJHI S, LIU Zilong, et al. New sets of even-length binary Z-complementary pairs with asymptotic ZCZ ratio of 3/4[J]. IEEE Signal Processing Letters, 2018, 25(7): 970–973. doi: 10.1109/LSP.2018.2834143
[13]	CHEN Chaoyu and PAI Chengyu. Binary Z-complementary pairs with bounded peak-to-mean envelope power ratios[J]. IEEE Communications Letters, 2019, 23(11): 1899–1903. doi: 10.1109/LCOMM.2019.2934692
[14]	LI Xudong, FAN Pingzhi, TANG Xiaohu, et al. Existence of binary Z-complementary pairs[J]. IEEE Signal Processing Letters, 2011, 18(1): 63–66. doi: 10.1109/LSP.2010.2095459
[15]	ADHIKARY A R, MAJHI S, LIU Zilong, et al. New optimal binary Z-complementary pairs of odd lengths[C]. 2017 Eighth International Workshop on Signal Design and Its Applications in Communications (IWSDA), Sapporo, Japan, 2017: 14–18.
[16]	XIE Chunlei and SUN Yujuan. Constructions of even-period binary Z-complementary pairs with large ZCZs[J]. IEEE Signal Processing Letters, 2018, 25(8): 1141–1145. doi: 10.1109/LSP.2018.2848102
[17]	SHEN Bingsheng, YANG Yang, ZHOU Zhengchun, et al. New optimal binary Z-complementary pairs of odd length 2^m+3[J]. IEEE Signal Processing Letters, 2019, 26(12): 1931–1934. doi: 10.1109/LSP.2019.2954805
[18]	ZENG Fanxin, HE Xiping, ZHANG Zhenyu, et al. Optimal and Z-optimal Type-II odd-length binary Z-complementary pairs[J]. IEEE Communications Letters, 2020, 24(6): 1163–1167. doi: 10.1109/LCOMM.2020.2977897
[19]	GU Zhi, ZHOU Zhengchun, WANG Qi, et al. New construction of optimal Type-II binary Z-complementary pairs[J]. IEEE Transactions on Information Theory, 2021, 67(6): 3497–3508. doi: 10.1109/TIT.2020.3007670
[20]	TIAN Shucong, YANG Meng, and WANG Jianpeng. Two constructions of binary Z-complementary pairs[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2021, E104.A(4): 768–772. doi: 10.1587/transfun.2020EAL2069
[21]	LIU Zilong, GUAN Yongliang, and PARAMPALLI U. On optimal binary Z-complementary pair of odd period[C]. 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 2013: 3125–3129.