Track Segment Association of Automatic Identification System and Dual-frequency High-Frequency Surface Wave Radar Based on Improved Gale-Shapley Algorithm
-
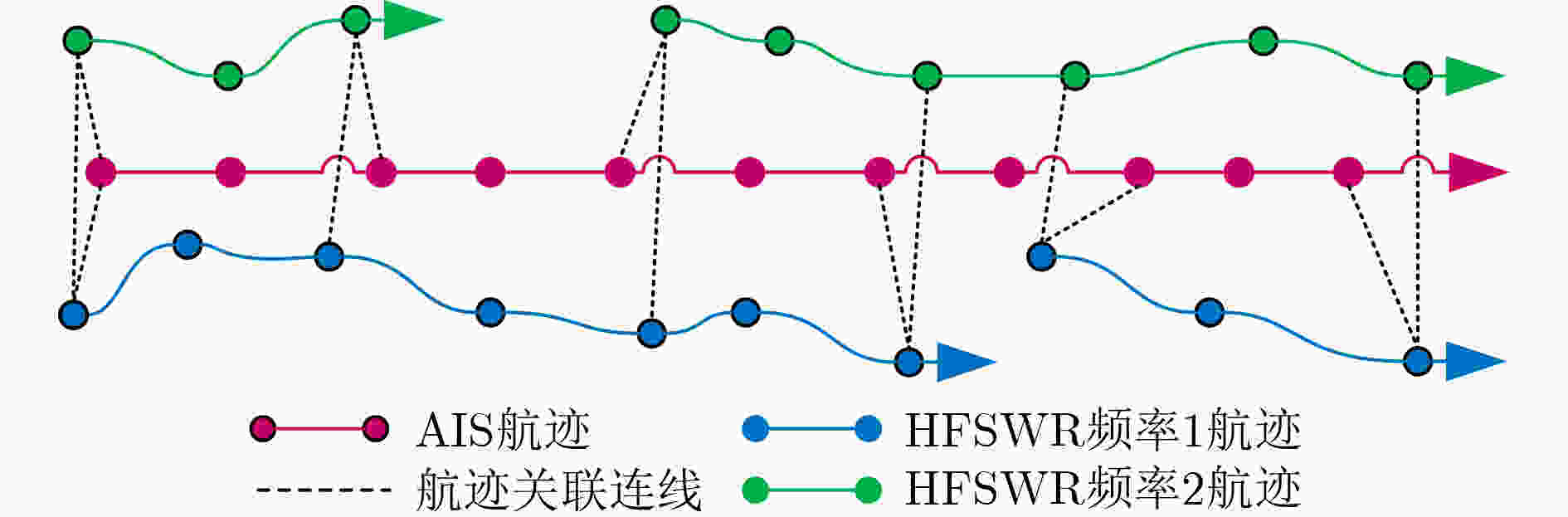
摘要: 高频地波雷达(HFSWR)可以实现大范围海上船只目标的连续探测,但是海杂波等干扰因素的影响容易造成跟踪航迹的断裂。目前关于地波雷达航迹关联的研究中,通常忽略了航迹断裂的情况,将航迹关联视为二分图匹配问题,这会导致可能将单一目标的断裂航迹判断为多个目标,从而引起目标的误关联。针对上述情况,该文结合模糊综合评判和迭代搜索算法,首次将盖尔-沙普利(GS)算法引入航迹关联领域,并且对其进行改进以满足航迹断裂时的多对多航迹关联情况,提出了改进的盖尔-沙普利(IGS)算法。在该算法中,通过计算航迹之间的模糊综合评判值来得到航迹之间的倾向度序列,再由迭代搜索对航迹进行聚类以获得航迹集群,最后将航迹集群及倾向度序列输入盖尔-沙普利算法来进行数轮博弈以给出关联结果。利用双频率高频地波雷达和船只自动识别系统(AIS)的仿真数据与实测数据进行实验测试,实验结果表明:所提出的算法解决了在航迹断裂情况下的多传感器航迹关联问题,且在密集区域的航迹关联效果优于传统算法。Abstract: Large-range maritime vessel targets can be detected continuously by High-Frequency Surface Wave Radar (HFSWR), but the tracking trajectory of the target is easily broken in the presence of disturbing factors such as sea clutter. In current studies on HFSWR track association, the case of broken tracks is usually ignored and the track association is considered as a bipartite graph matching problem, which can lead to the possibility of judging broken tracks of a single target as multiple targets, and thus wrong target association results are obtained. For the above situation, fuzzy integrated evaluation and iterative search algorithms are considered in this paper. The Gale-Shapley (GS) algorithm is introduced into the field of track association for the first time, and it is improved to satisfy the many-to-many track association case when the track is broken , the Improved Gale-Shapley (IGS) algorithm is proposed. In this algorithm, the tendency sequences between the tracks can be obtained by calculating the fuzzy composite judgment values between the tracks. Then, the tracks are clustered by an iterative search method to obtain the track clusters. Finally, the track clusters and the propensity sequences are fed into the Gale-Shapley algorithm to perform several rounds of games to give the association results. The measured data and simulation data of dual-frequency HFSWR and Automatic Identification System (AIS) are used for experimental tests. Experimental tests are conducted using simulated and measured data from dual-frequency HFSWR and AIS. The experimental results show that the multi-sensor track association problem in the case of track break can be solved by the proposed algorithm, and the track association effect in dense areas is better than that of the conventional algorithm.
-
表 1 航迹集G1详细情况
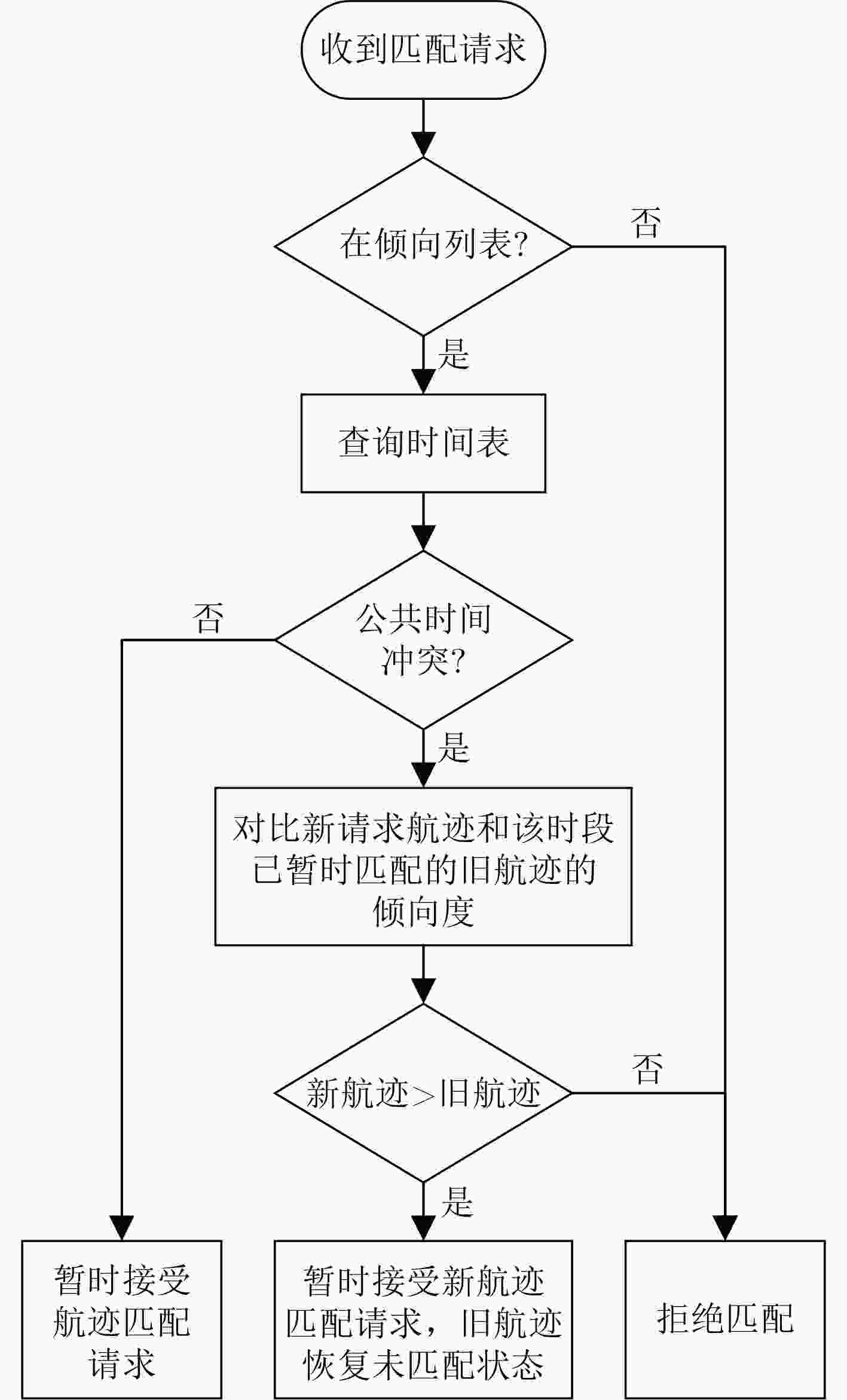
航迹标号 倾向度表(正序) 航迹所属时间(min) A1 B1, B3, B2 03~19 A2 B3, B1, B2 30~43 A3 B3, B2, B1 23~46 A4 B1, B2, B3 21~49 B1 A2, A3, A4, A1 06~30 B2 A3, A4, A1, A2 12~36 B3 A3, A4, A2, A1 15~51 表 2 航迹集G1匹配过程
邀约轮数 该轮邀约结束时的匹配结果 第1轮 A1-B1; A2-无 A3-B3; A4-B1 第2轮 A1-无; A2-B1; A3-B3; A4-无 第3轮 A1-B2; A2-B1; A3-B3; A4-B2 表 3 航迹关联结果性能分析
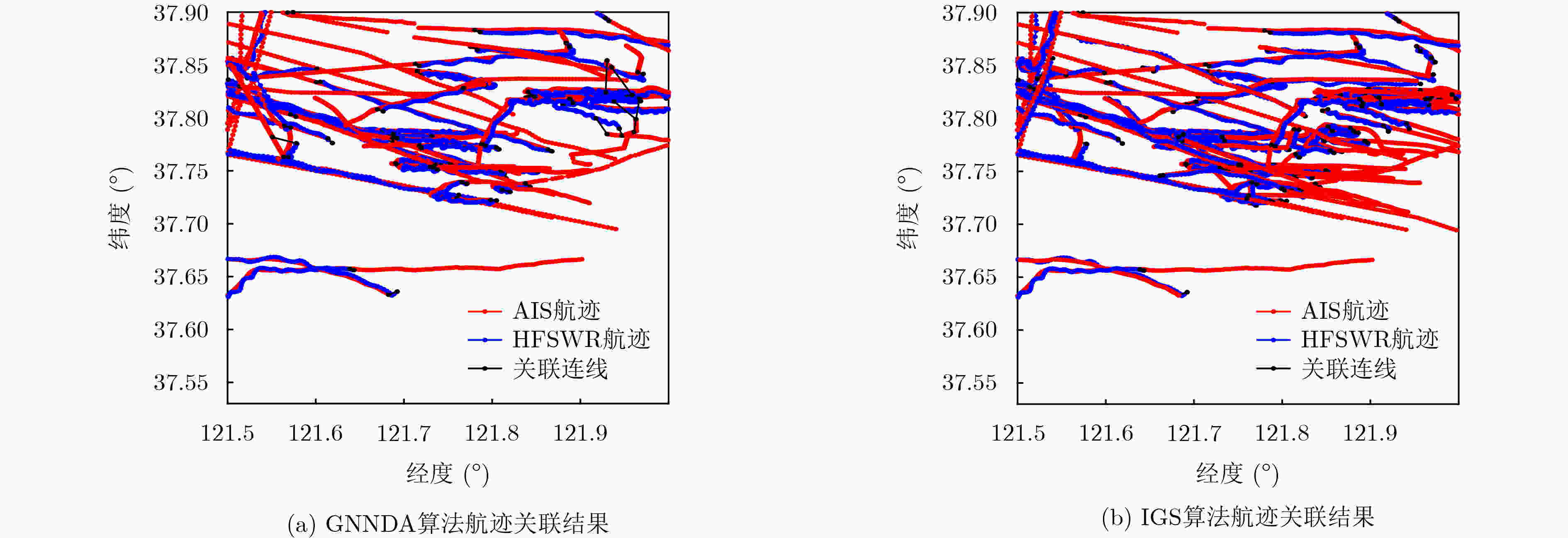
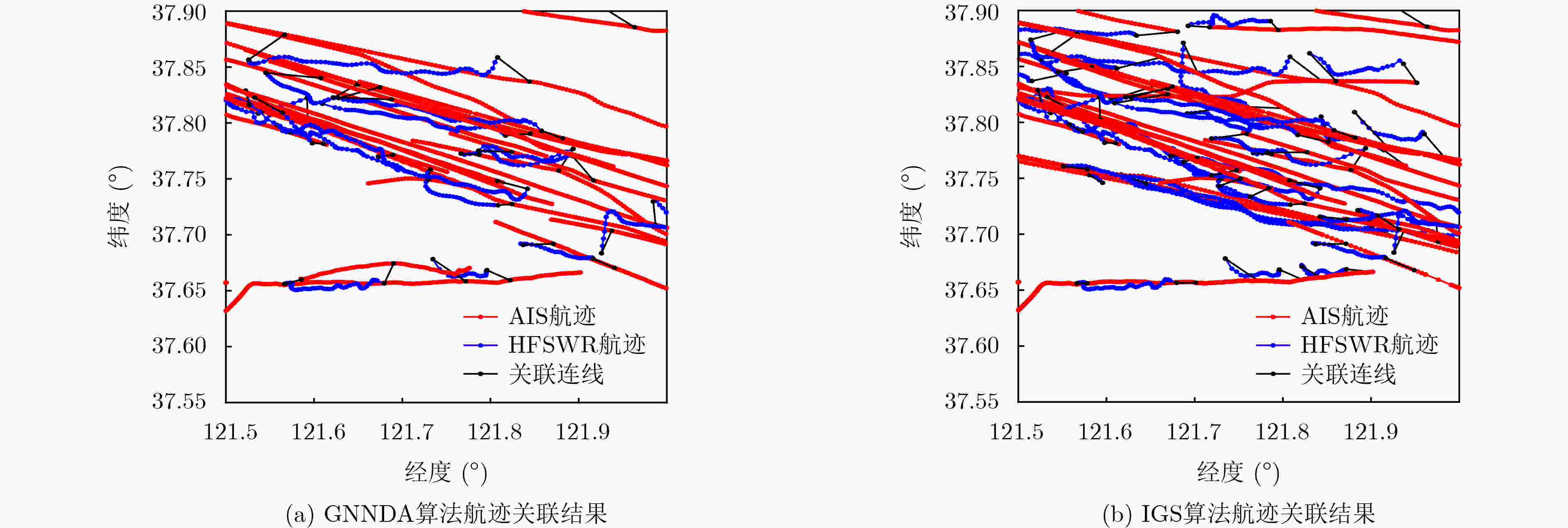
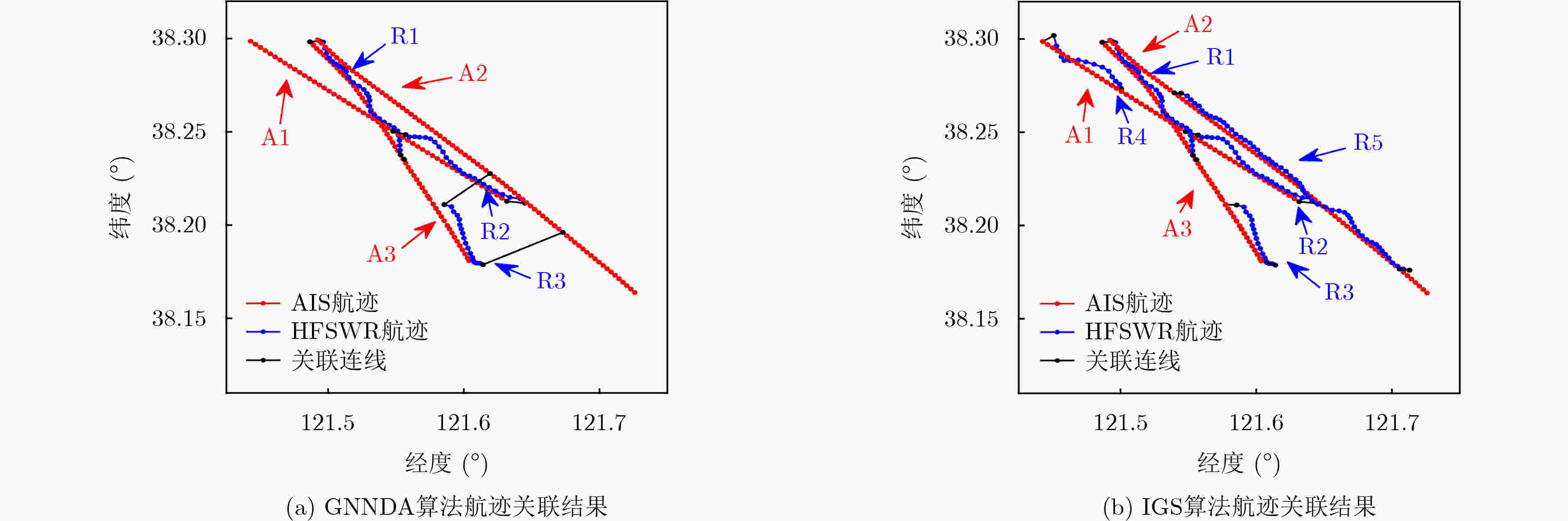
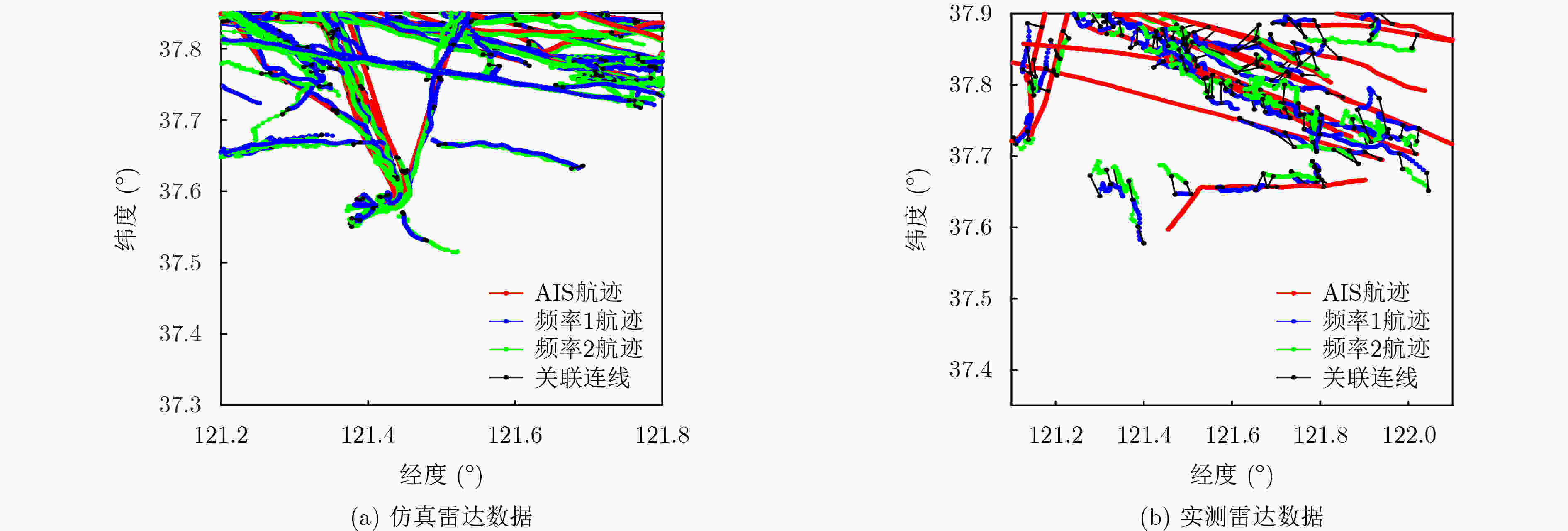
实验数据和所用算法 关联比例(%) 关联正确率(%) 距离RMSE(km) 方位RMSE(°) 速度RMSE(km/h) 计算耗时(s) 仿真数据GNNDA 48.20 88.81 0.4077 0.2759 0.4401 5.73 仿真数据IGS 75.18 97.13 0.3863 0.2406 0.3826 11.82 实测数据GNNDA 42.06 未知 1.9930 1.8935 0.5024 6.49 实测数据IGS 60.75 未知 1.8783 1.6710 0.3438 13.05 表 4 实测数据非合作目标双频航迹关联个例分析(km/h)
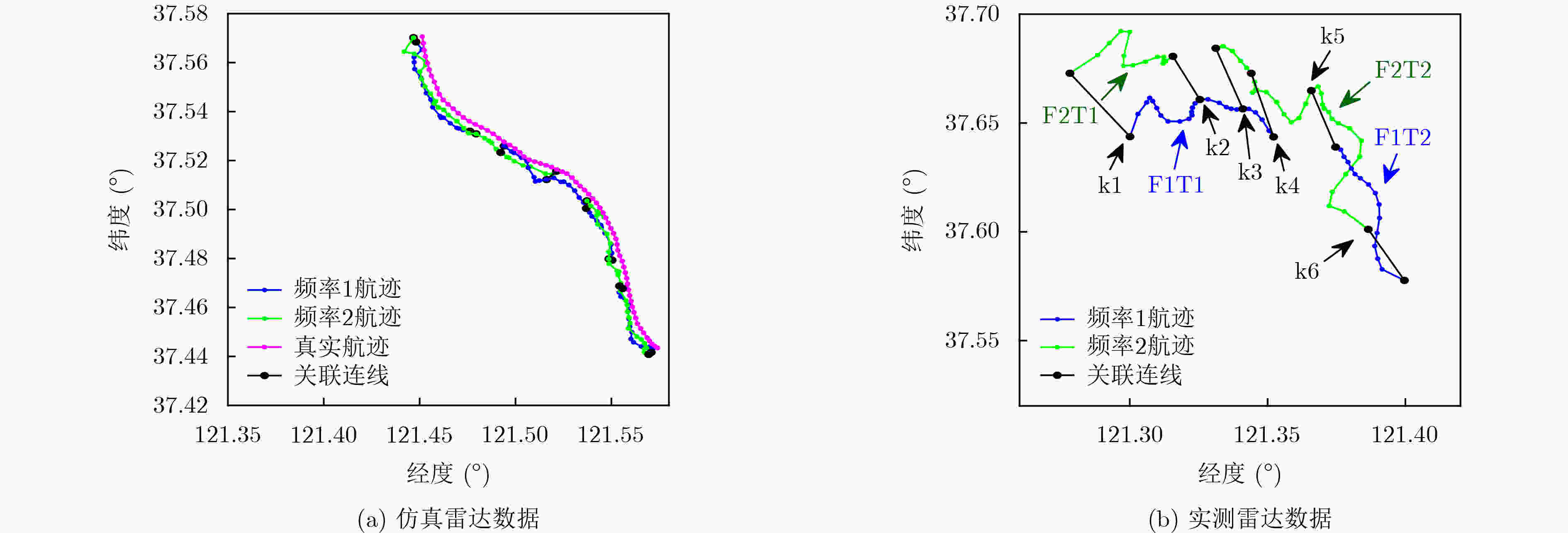
航迹名 航迹时间 k1点速度 k2点速度 k3点速度 k4点速度 k5点速度 k6点速度 F1T1 09:57~10:22 –13.48 –12.26 –12.86 –13.33 无数值 无数值 F1T2 10:31~10:46 无数值 无数值 无数值 无数值 –13.23 –13.02 F2T1 09:57~10:12 –13.31 –12.48 无数值 无数值 无数值 无数值 F2T2 10:18~10:46 无数值 无数值 –12.43 –13.05 –13.01 –12.78 -
[1] JI Yonggang, ZHANG Jie, MENG Junmin, et al. Point association analysis of vessel target detection with SAR, HFSWR and AIS[J]. Acta Oceanologica Sinica, 2014, 33(9): 73–81. doi: 10.1007/s13131-014-0498-2 [2] 刘根旺, 刘永信, 纪永刚, 等. 基于模糊双门限的高频地波雷达与AIS目标航迹关联方法[J]. 系统工程与电子技术, 2016, 38(3): 557–562. doi: 10.3969/j.issn.1001-506X.2016.03.13LIU Genwang, LIU Yongxin, JI Yonggang, et al. Track association for high-frequency surface wave radar and AIS based on fuzzy double threshold theory[J]. Systems Engineering and Electronics, 2016, 38(3): 557–562. doi: 10.3969/j.issn.1001-506X.2016.03.13 [3] SUN Weifeng, HUANG Weimin, JI Yonggang, et al. A vessel azimuth and course joint re-estimation method for compact HFSWR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 1041–1051. doi: 10.1109/TGRS.2019.2943065 [4] SUN Weifeng, DAI Yongshou, JI Yonggang, et al. Vessel target tracking exploiting frequency diversity for dual-frequency HFSWR[C]. 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–4. [5] NIKOLIC D, STOJKOVIC N, and LEKIC N. Maritime over the horizon sensor integration: High frequency surface-wave-radar and automatic identification system data integration algorithm[J]. Sensors, 2018, 18(4): 1147. doi: 10.3390/s18041147 [6] STOJKOVIC N, NIKOLIC D, and PUZOVIĆ S. Density based clustering data association procedure for real–time HFSWRs tracking at OTH distances[J]. IEEE Access, 2020, 8: 39907–39919. doi: 10.1109/ACCESS.2020.2976481 [7] WANG Jun, ZENG Yajun, WEI Shaoming, et al. Multi-sensor track-to-track association and spatial registration algorithm under incomplete measurements[J]. IEEE Transactions on Signal Processing, 2021, 69: 3337–3350. doi: 10.1109/TSP.2021.3084533 [8] NAZARI M, PASHAZADEH S, and MOHAMMAD-KHANLI L. An adaptive density-based fuzzy clustering track association for distributed tracking system[J]. IEEE Access, 2019, 7: 135972–135981. doi: 10.1109/ACCESS.2019.2941184 [9] 靳冰洋, 刘峥, 秦基凯. 基于灰色关联度的两级实时航迹关联算法[J]. 兵工学报, 2020, 41(7): 1330–1338. doi: 10.3969/j.issn.1000-1093.2020.07.010JIN Bingyang, LIU Zheng, and QIN Jikai. Two-stage real-time track correlation algorithm based on gray correlation[J]. Acta Armamentarii, 2020, 41(7): 1330–1338. doi: 10.3969/j.issn.1000-1093.2020.07.010 [10] 蔡昌恺, 朱浩, 余仁伟, 等. 基于航迹全局和局部混合特征的航迹关联算法[J]. 仪器仪表学报, 2020, 41(10): 32–42. doi: 10.19650/j.cnki.cjsi.J2006793CAI Changkai, ZHU Hao, YU Renwei, et al. Track-to-track association by the global and local mixture feature[J]. Chinese Journal of Scientific Instrument, 2020, 41(10): 32–42. doi: 10.19650/j.cnki.cjsi.J2006793 [11] RAGHU J, SRIHARI P, THARMARASA R, et al. Comprehensive track segment association for improved track continuity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2463–2480. doi: 10.1109/TAES.2018.2820364 [12] 周学平, 李佳杰, 赵晓莲, 等. 基于匈牙利法的机载雷达中断航迹关联[J]. 现代雷达, 2021, 43(6): 42–48. doi: 10.16592/j.cnki.1004-7859.2021.06.008ZHOU Xueping, LI Jiajie, ZHAO Xiaolian, et al. Airborne radar track segment association based on hungarian algorithm[J]. Modern Radar, 2021, 43(6): 42–48. doi: 10.16592/j.cnki.1004-7859.2021.06.008 [13] CHANG W, JAU Y T, SU S L, et al. Gale-Shapley-algorithm based resource allocation scheme for device-to-device communications underlaying downlink cellular networks[C]. 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 2016: 1–6. [14] PITTEL B. One-sided version of Gale-Shapley proposal algorithm and its likely behavior under random preferences[J]. Discrete Applied Mathematics, 2021, 292: 1–18. doi: 10.1016/j.dam.2020.12.020 -





 下载:
下载:


 下载:
下载:
