Number and Position Estimation Algorithm of Space Group Targets Based on Probability Hypothesis Density Filter and Dynamic Model
-
摘要: 空间目标具有射程远、速度快等特点,为了有效解决密集性高、可分性差的高速空间目标群饱和攻击问题,实现非合作空间群目标数量和位置的尽早分辨,该文基于随机有限集(RFS)理论和动力学方程约束研究了空间“团状”目标数量和位置分辨问题,提出目标监测早期解决大量距离靠近、运动特征差异不明显的高速空间群目标数量和位置估计的相关算法,该算法利用概率假设密度(PHD)滤波器能够解决未知时变环境下目标个数与状态估计的特点,将高斯混合PHD (GM-PHD)滤波和空间目标动力学方程相结合,在解决不可分辨空间群目标数量和位置估计问题的同时,充分利用空间目标动力学方程对群内目标状态进行实时调整,提高空间目标位置状态估计精度,解决不可分辨空间目标群边跟踪边分辨问题,相关算法可为空间群目标数量和群内特殊价值个体目标位置尽快分辨、连续稳定跟踪和可靠动向预报等提供数据基础。Abstract: Space targets have the characteristics of wide coverage, fast speed, high target density and similar movement, which lead to that in a relatively long time these targets can not be effectively distinguished. How to distinguish effectively the number and position of these non-cooperative space targets as soon as possible is very important. Therefore, based on Random Finite Set (RFS) theory and dynamic model of space targets, the number and position estimation method of unresolved space group targets is studied in this paper, which can effectively estimate the number and position of space group targets with high-speed and small spatial distribution range in the early stage of target monitoring. This method makes full use of the characteristics of Probability Hypothesis Density (PHD) filter, which can solve the number and state estimation of targets in unknown time-varying environment. The Gaussian Mixture PHD (GM-PHD) filter is combined with the space target dynamic equation to estimate the number of unresolved space targets, and the target state are estimated more effectively by the constraint of the dynamic equation. At the same time of target tracking, the resolution problem of unresolved space group targets can be solved. The correlation algorithms can provide data basis for state estimation, continuous stable tracking and reliable trajectory prediction of special value individual target in the group.
-
表 1 仿真参数设置
参数名称 参数值 测量时间 0~860 s 关机点空间目标x轴速度 3000 m/s 关机点空间目标y轴速度 3000 m/s 关机点空间目标z轴速度 3000 m/s 关机点空间目标经度 0° 关机点空间目标纬度 0° 关机点空间目标高度 80 km 雷达站经度 9.5° 雷达站纬度 1.5° 雷达站大地高程 0 m -
[1] LIAN Feng, HAN Chongzhao, LIU Weifeng, et al. Sequential monte carlo implementation and state extraction of the group probability hypothesis density filter for partly unresolvable group targets-tracking problem[J]. IET Radar, Sonar & Navigation, 2010, 4(5): 685–702. doi: 10.1049/iet-rsn.2009.0109 [2] 连峰, 元向辉, 陈辉. 基于势概率假设密度滤波器的不可分辨目标跟踪算法[J]. 系统工程与电子技术, 2013, 35(12): 2445–2451. doi: 10.3969/j.issn.1001-506X.2013.12.01LIAN Feng, YUAN Xianghui, and CHEN Hui. Tracking unresolved targets using cardinalized probability hypothesis density filter[J]. Systems Engineering and Electronics, 2013, 35(12): 2445–2451. doi: 10.3969/j.issn.1001-506X.2013.12.01 [3] 李昌玺, 周焰, 郭戈, 等. 弹道导弹群目标跟踪技术综述[J]. 战术导弹技术, 2015(3): 66–73. doi: 10.16358/j.issn.1009-1300.2015.03.13LI Changxi, ZHOU Yan, GUO Ge, et al. Summary of group tracking technology based on ballistic missile[J]. Tactical Missile Technology, 2015(3): 66–73. doi: 10.16358/j.issn.1009-1300.2015.03.13 [4] 姜琦, 王锐, 周超, 等. 基于代数图论的修正贝叶斯群目标航迹起始算法[J]. 电子与信息学报, 2021, 43(3): 531–538. doi: 10.11999/JEIT200449JIANG Qi, WANG Rui, ZHOU Chao, et al. Modified Bayesian group target track initiation algorithm based on algebraic graph theory[J]. Journal of Electronics &Information Technology, 2021, 43(3): 531–538. doi: 10.11999/JEIT200449 [5] 周万幸. 空间导弹目标的捕获和处理[M]. 北京: 电子工业出版社, 2013: 109–154.ZHOU Wanxing. Acquisition and Processing of Space Missile Target[M]. Beijing: Publishing House of Electronics Industry, 2013: 109–154. [6] HE You, XIU Jianjuan, and GUAN Xin. Radar Data Processing with Applications[M]. Singapore: Wiley, 2016: 203–247. [7] 靳标, 李聪, 张贞凯. 回波幅度信息辅助的群目标航迹起始方法[J]. 雷达学报, 2020, 9(4): 723–729. doi: 10.12000/JR19088JIN Biao, LI Cong, and ZHANG Zhenkai. Group target track initiation method aided by echo amplitude information[J]. Journal of Radars, 2020, 9(4): 723–729. doi: 10.12000/JR19088 [8] 杜明洋, 毕大平, 王树亮. 群目标跟踪关键技术研究进展[J]. 电光与控制, 2019, 26(4): 59–65,90. doi: 10.3969/j.issn.1671-637X.2019.04.012DU Mingyang, BI Daping, and WANG Shuliang. Advances in key technologies of group target tracking[J]. Electronics Optics &Control, 2019, 26(4): 59–65,90. doi: 10.3969/j.issn.1671-637X.2019.04.012 [9] 陈辉, 杜金瑞, 韩崇昭. 基于星凸形随机超曲面模型多扩展目标多伯努利滤波器[J]. 自动化学报, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130CHEN Hui, DU Jinrui, and HAN Chongzhao. A multiple extended target multi-bernouli filter based on star-convex random hypersurface model[J]. Acta Automatica Sinica, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130 [10] 甘林海, 王刚, 刘进忙, 等. 群目标跟踪技术综述[J]. 自动化学报, 2020, 46(3): 411–426. doi: 10.16383/j.aas.c180052GAN Linhai, WANG Gang, LIU Jinmang, et al. An overview of group target tracking[J]. Acta Automatica Sinica, 2020, 46(3): 411–426. doi: 10.16383/j.aas.c180052 [11] FELDMANN M, FRÄNKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409–1420. doi: 10.1109/TSP.2010.2101064 [12] ORGUNER U. A variational measurement update for extended target tracking with random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3827–3834. doi: 10.1109/TSP.2012.2192927 [13] 刘妹琴, 兰剑. 目标跟踪前沿理论与应用[M]. 北京: 科学出版社, 2015: 38–75.LIU Meiqin and LAN Jian. Theory and Application of Target Tracking Frontier[M]. Beijing: Science Press, 2015: 38–75. [14] LAN Jian and LI X R. Tracking of maneuvering non-ellipsoidal extended object or target group using random matrix[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2450–2463. doi: 10.1109/TSP.2014.2309561 [15] LI X R and JILKOV V P. Survey of maneuvering target tracking-part II: Ballistic target models[J]. SPIE, 2001, 4473: 559–581. [16] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part II: Motion models of ballistic and space targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 96–119. doi: 10.1109/TAES.2010.5417150 [17] 赵艳丽. 弹道导弹雷达跟踪与识别研究[D]. [博士论文], 国防科技大学, 2007: 16–52.ZHAO Yanli. Study on radar tracking and discrimination for ballistic missiles[D]. [Ph. D. dissertation], National University of Defense Technology, 2007: 16–52 . [18] 彭华甫, 黄高明, 田威, 等. 幅度及多普勒信息辅助的多目标跟踪算法[J]. 航空学报, 2018, 39(10): 322247. doi: 10.7527/S1000-6893.2018.22247PENG Huafu, HUANG Gaoming, TIAN Wei, et al. Multi-target tracking algorithm based on amplitude and Doppler information[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(10): 322247. doi: 10.7527/S1000-6893.2018.22247 [19] MAHLER R P S, 范红旗, 卢大威, 蔡飞, 译. 多源多目标统计信息融合进展[M]. 北京: 国防工业出版社, 2017: 145–165.MAHLER R P S, FAN Hongqi, LU Dawei, and CAI Fei. translation. Advances in Statistical Multisource-Multitarget Information Fusion[M]. Beijing: National Defense Industry Press, 2017: 145–165. [20] 吴卫华, 孙合敏, 蒋苏蓉, 等. 随机有限集目标跟踪[M]. 北京: 国防工业出版社, 2020: 91–102.WU Weihua, SUN Hemin, JIANG Surong, et al. Target Tracking with Random Finite Sets[M]. Beijing: National Defense Industry Press, 2020: 91–102. [21] 徐从安, 刘瑜, 熊伟, 等. 新生目标强度未知的双门限粒子PHD滤波器[J]. 航空学报, 2015, 36(12): 3957–3969. doi: 10.7527/S1000-6893.2015.0104XU Cong’an, LIU Yu, XIONG Wei, et al. A dual threshold particle PHD filter with unknown target birth intensity[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3957–3969. doi: 10.7527/S1000-6893.2015.0104 [22] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152–1178. doi: 10.1109/TAES.2003.1261119 [23] VO B N and MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104. doi: 10.1109/TSP.2006.881190 [24] 修建娟, 张敬艳, 董凯. 基于动力学模型约束的空间目标精确跟踪算法研究[J]. 电子学报, 2021, 49(4): 781–787. doi: 10.12263/DZXB.20200336XIU Jianjuan, ZHANG Jingyan, and DONG Kai. Precise tracking algorithm of space target based on dynamic model[J]. Acta Electronica Sinica, 2021, 49(4): 781–787. doi: 10.12263/DZXB.20200336 -





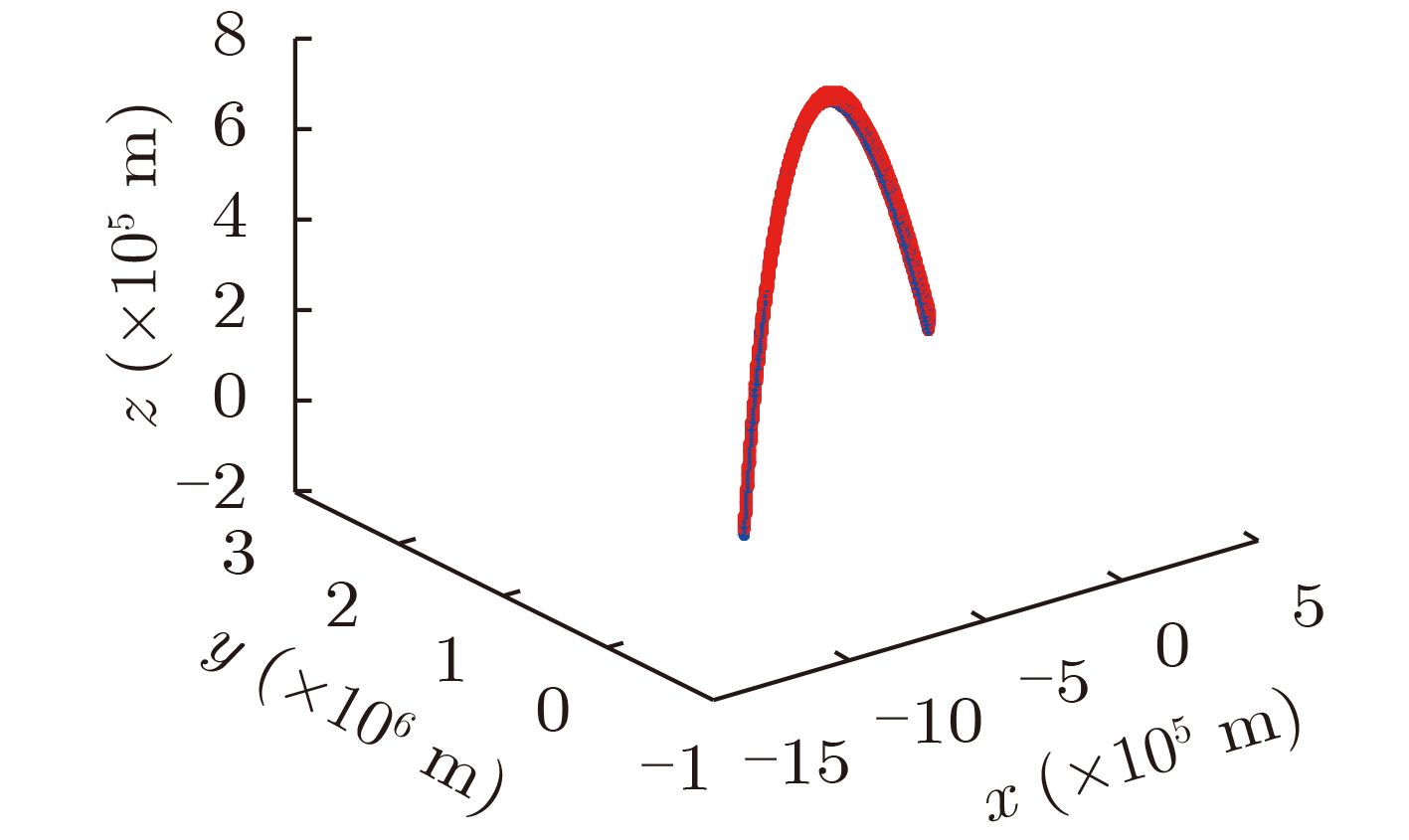
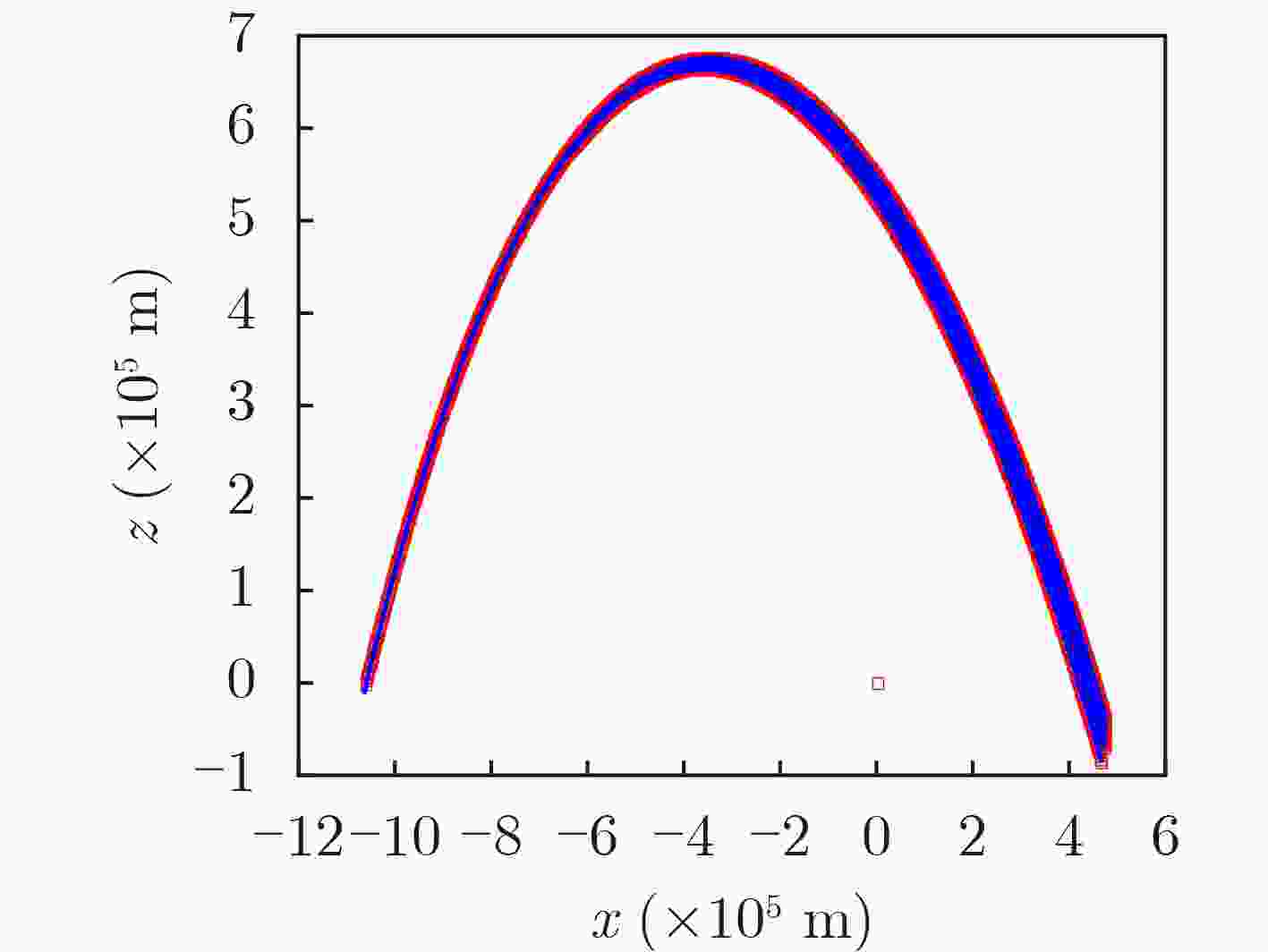
 下载:
下载:

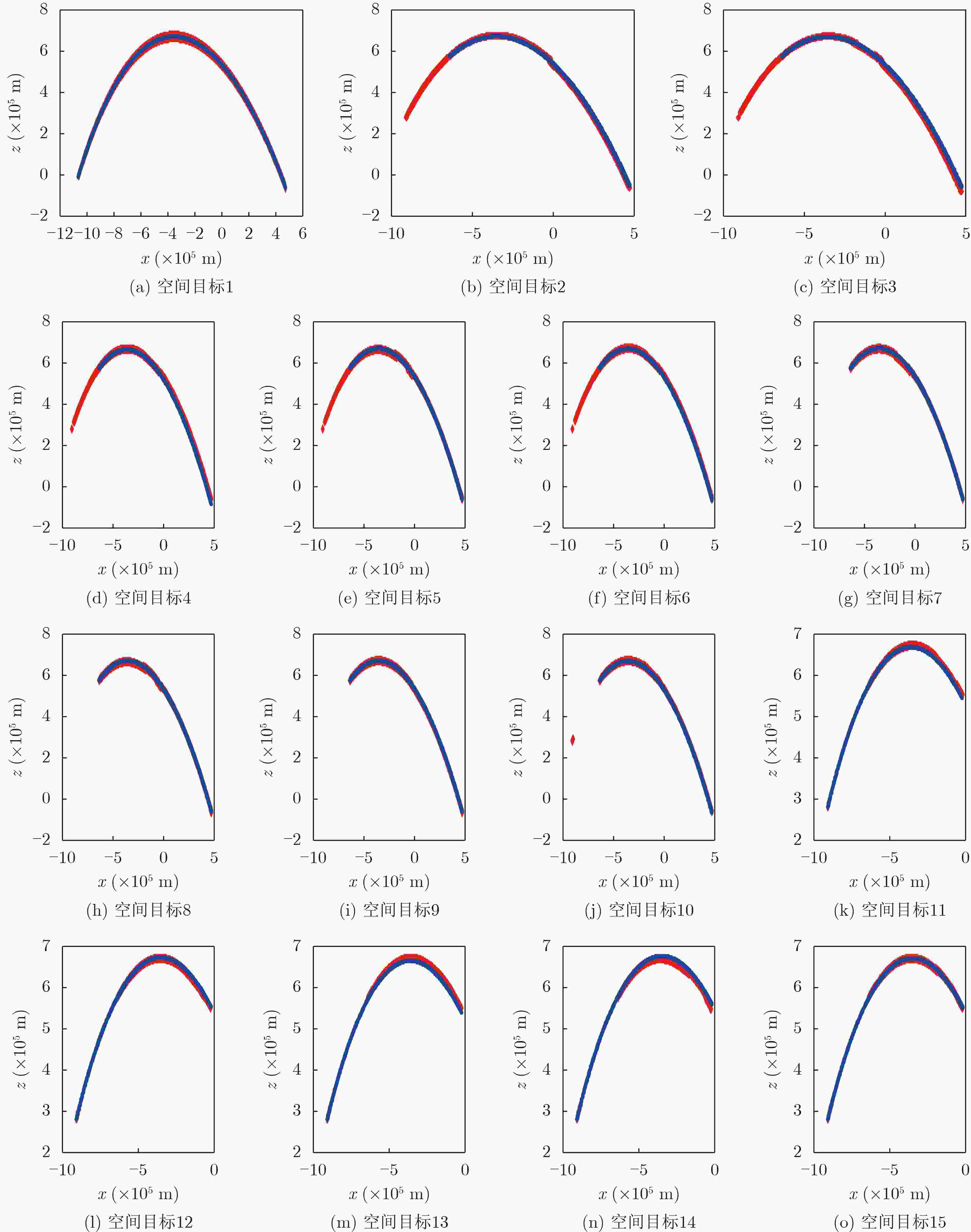
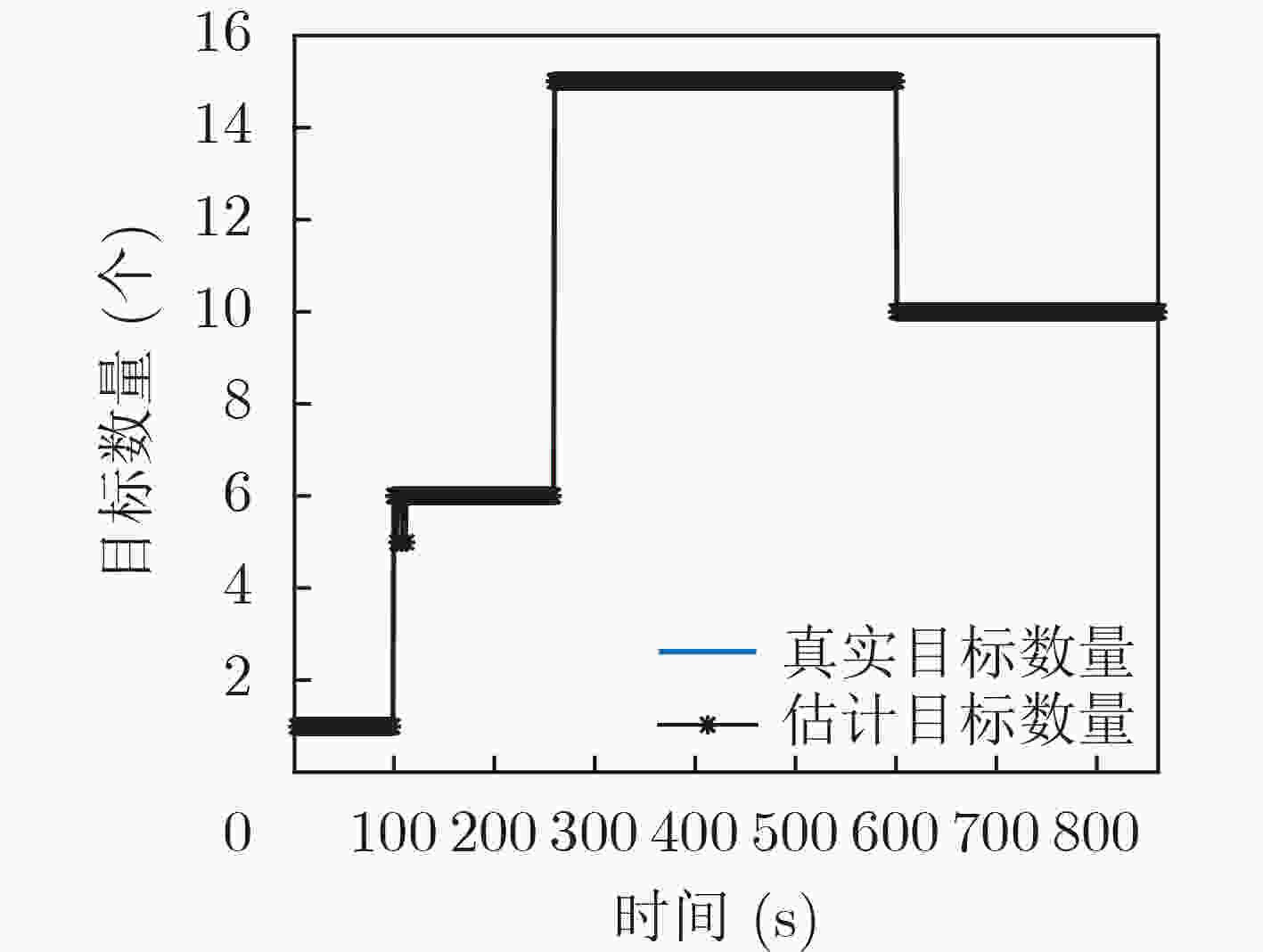
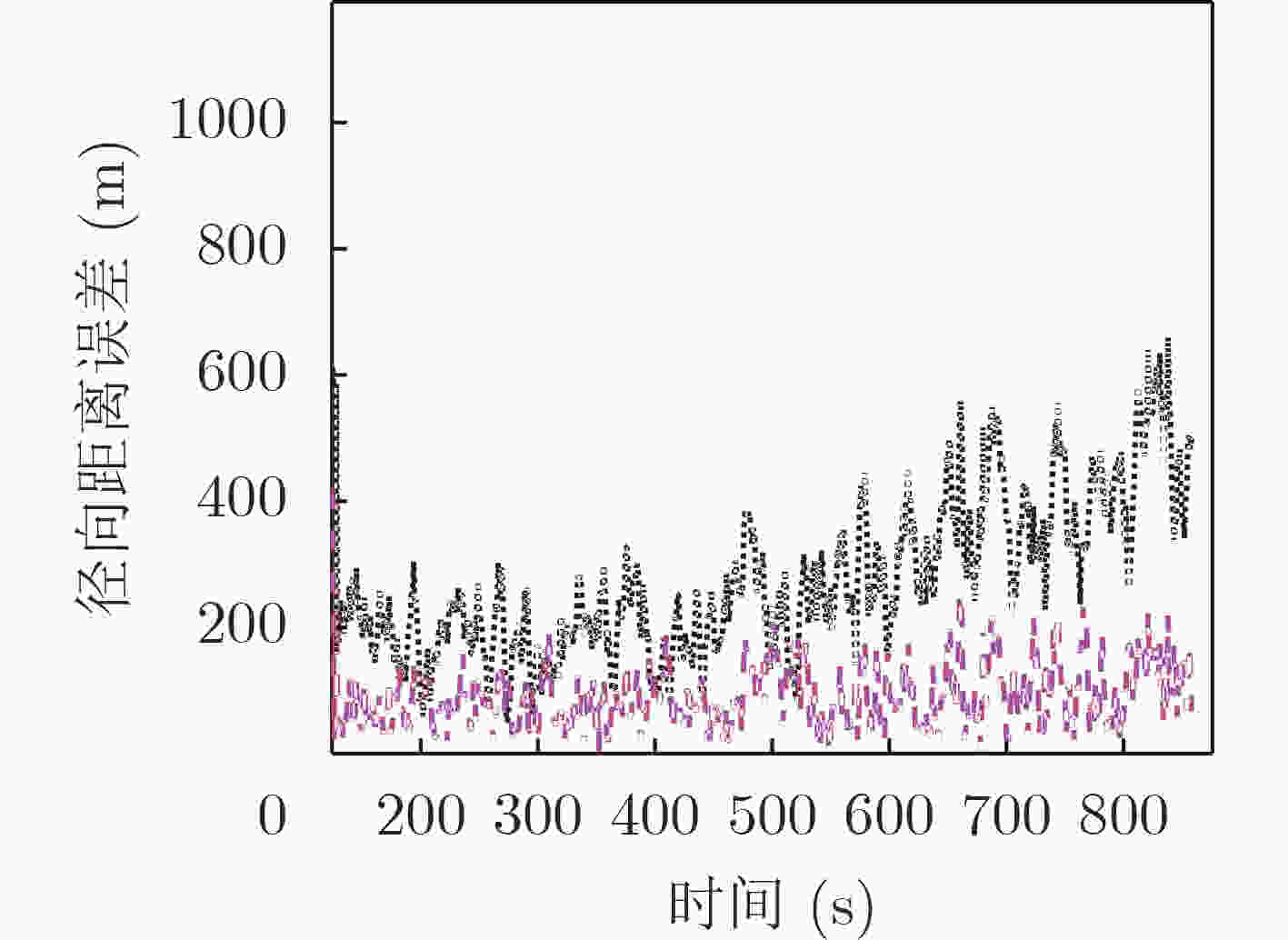
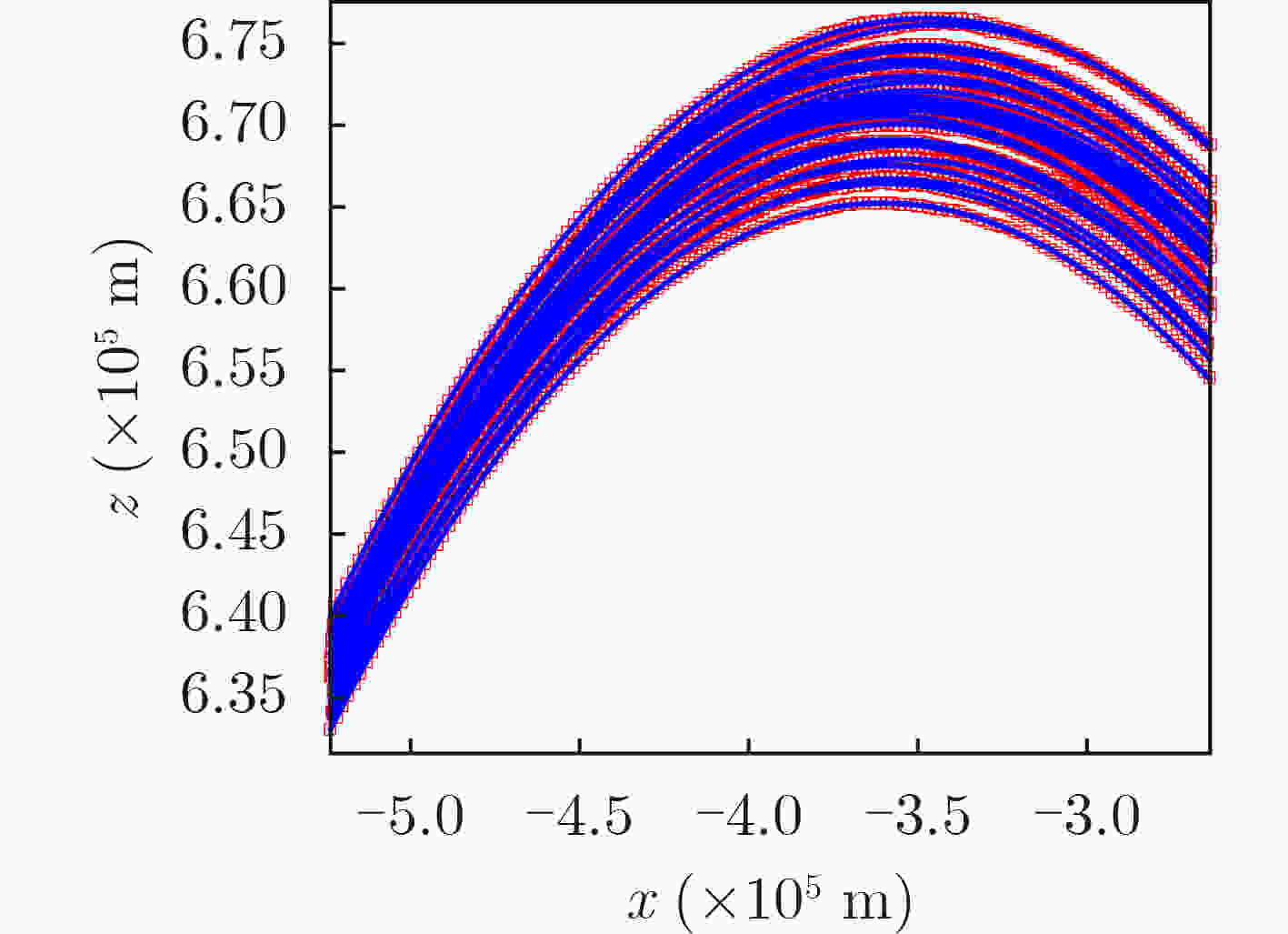
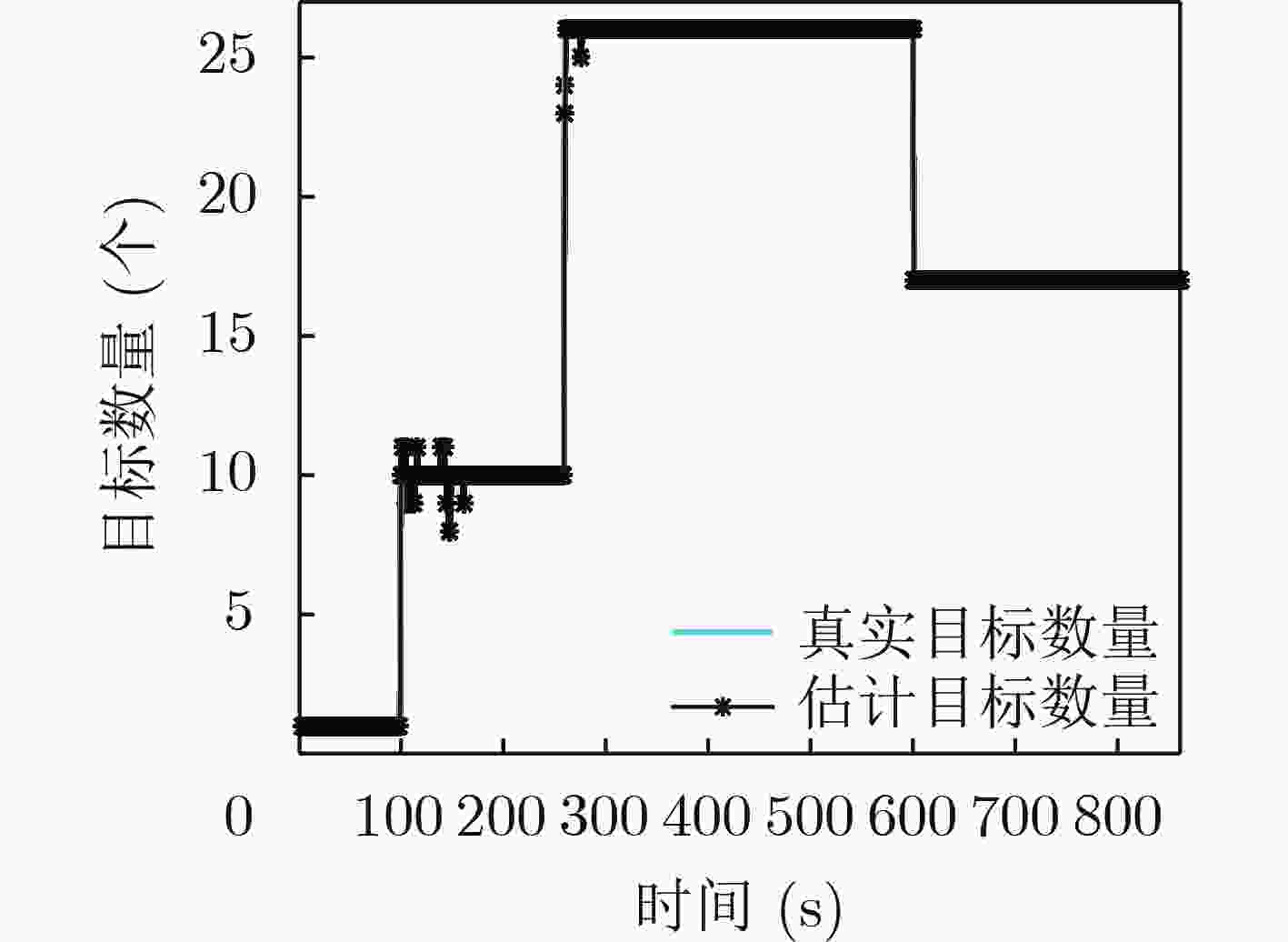
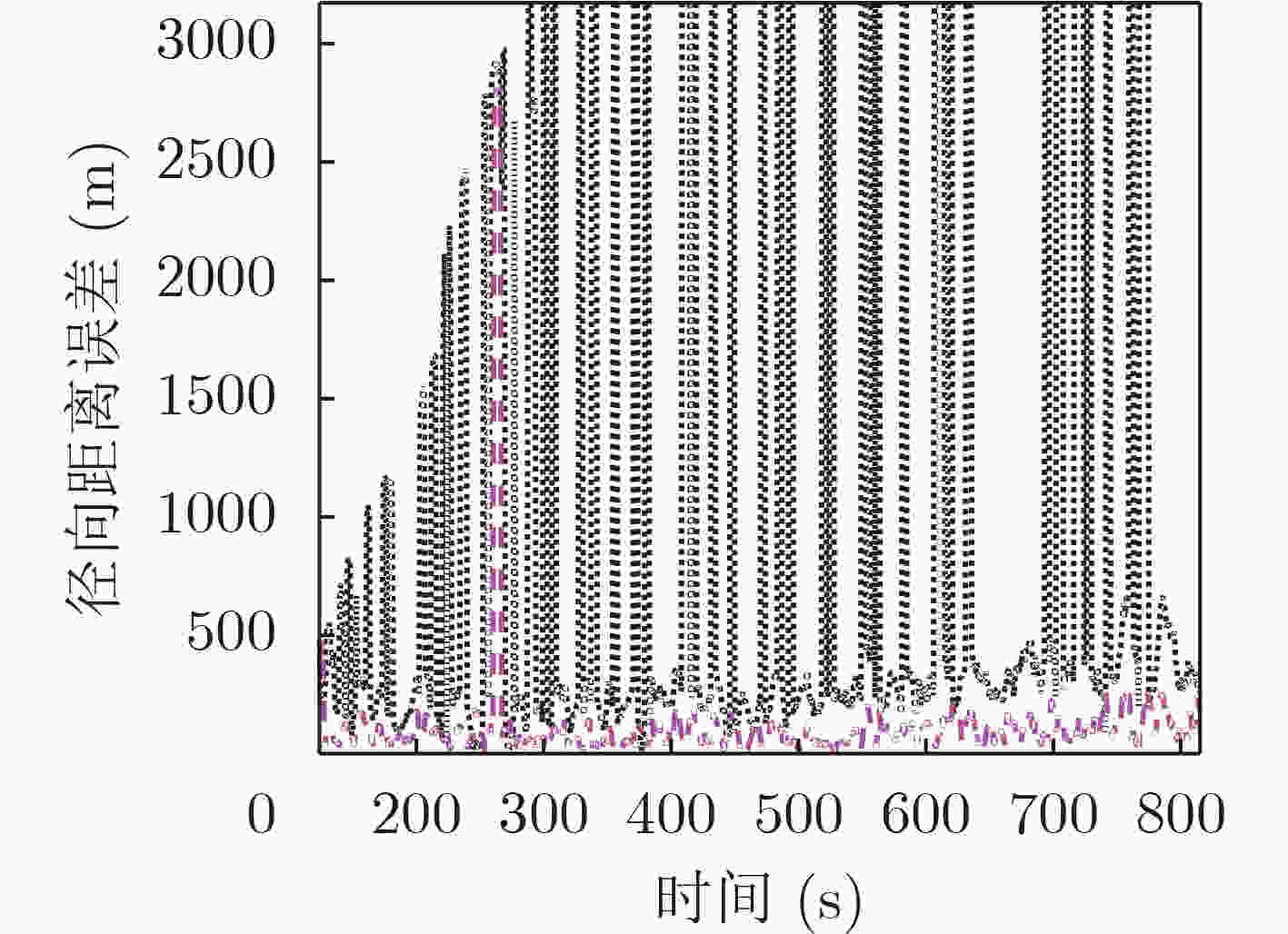
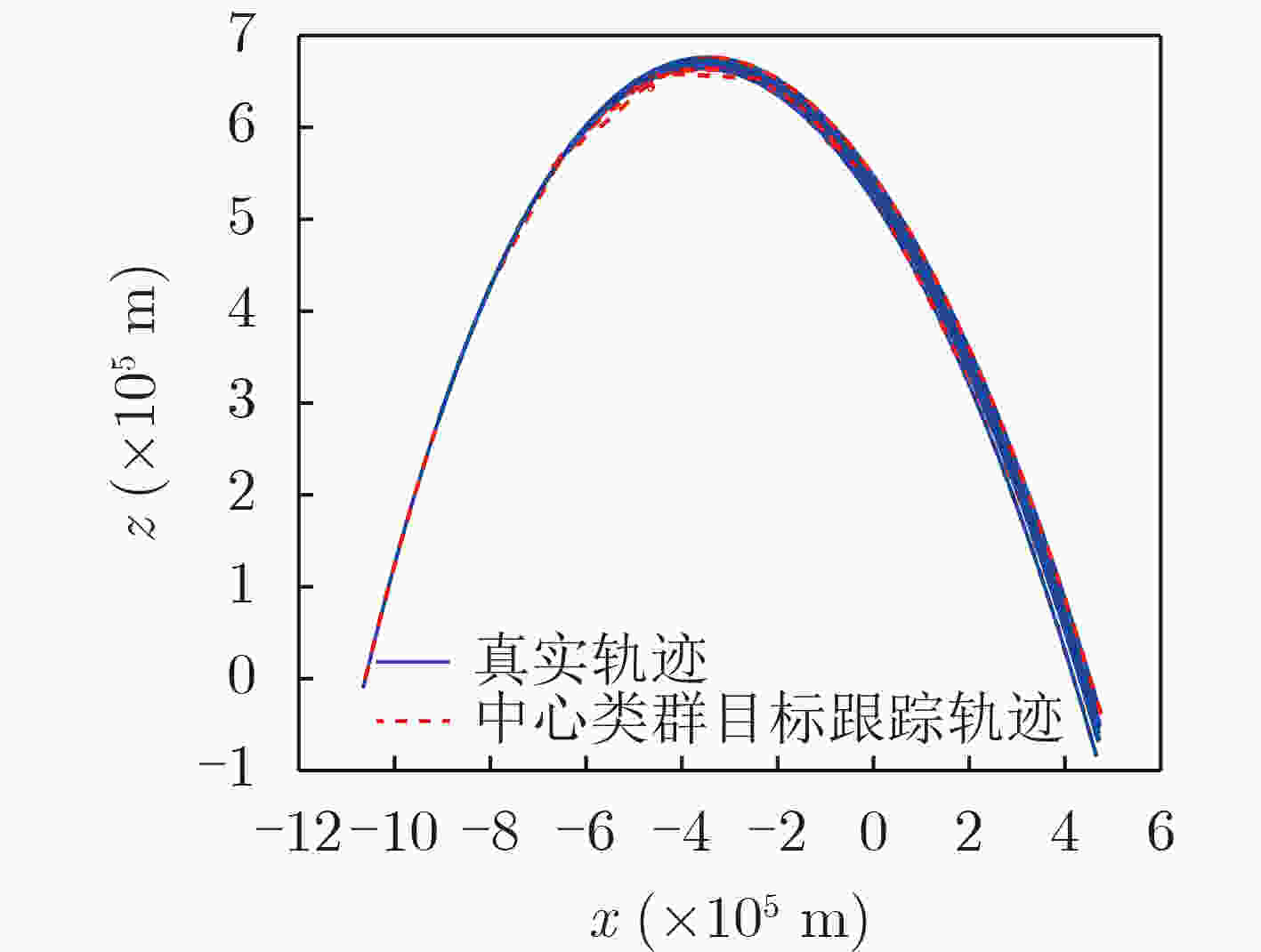
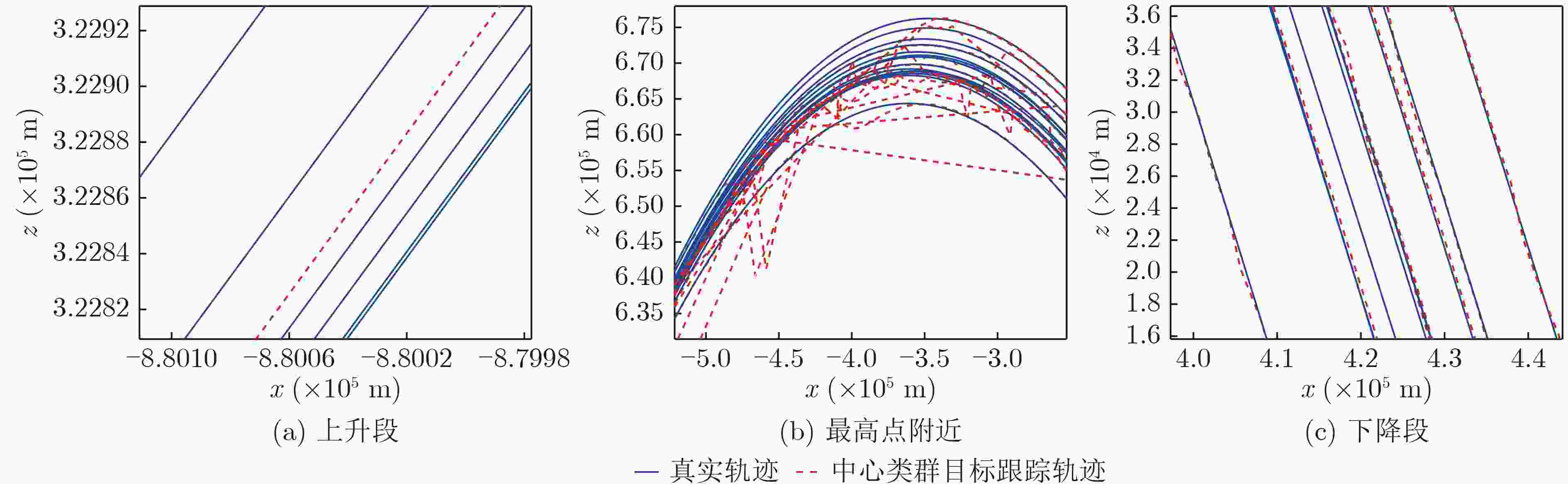


 下载:
下载:
