Low Complexity Equalization Algorithm of OCDM Systems in Doubly-Selective Channels
-
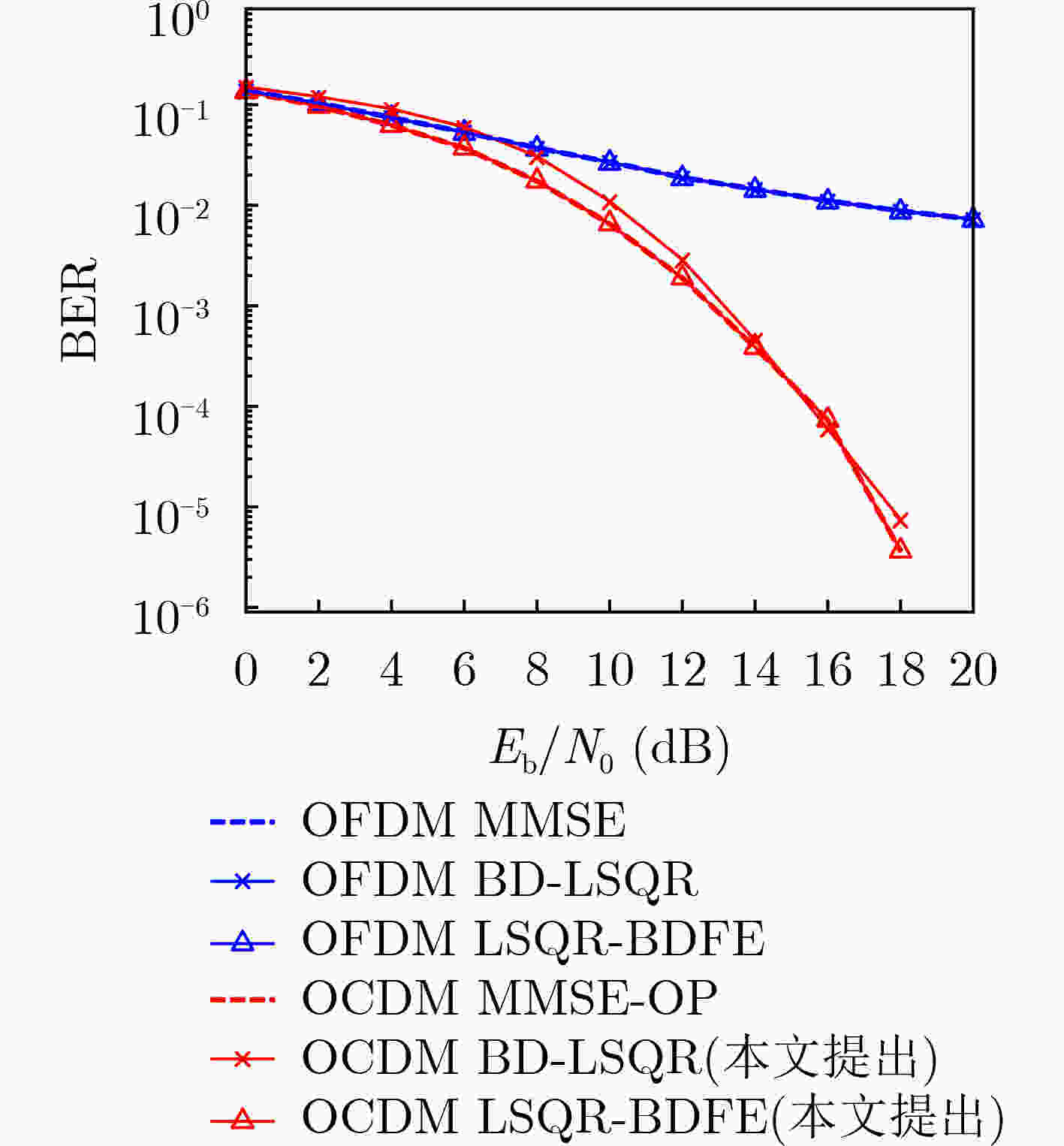
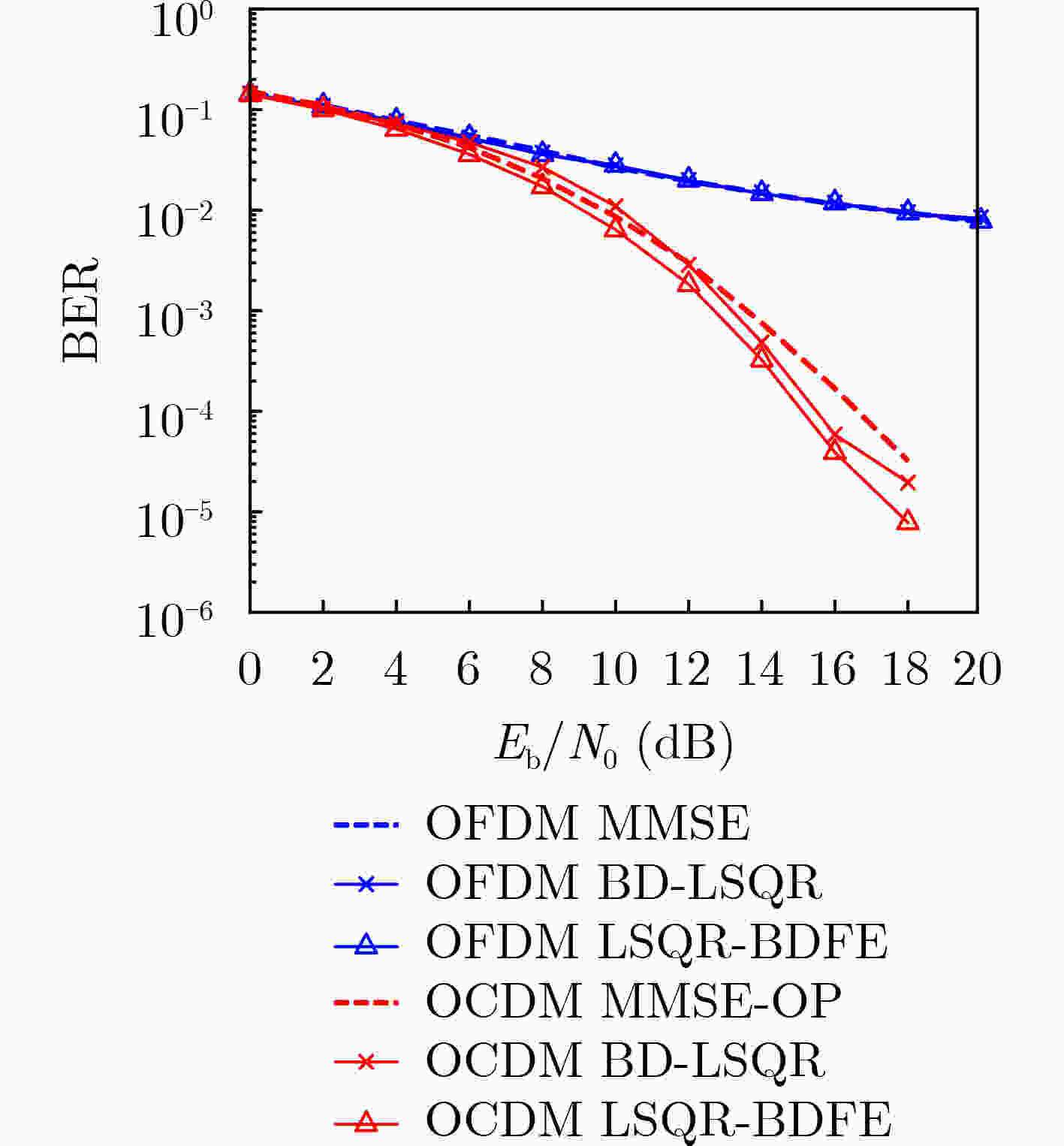
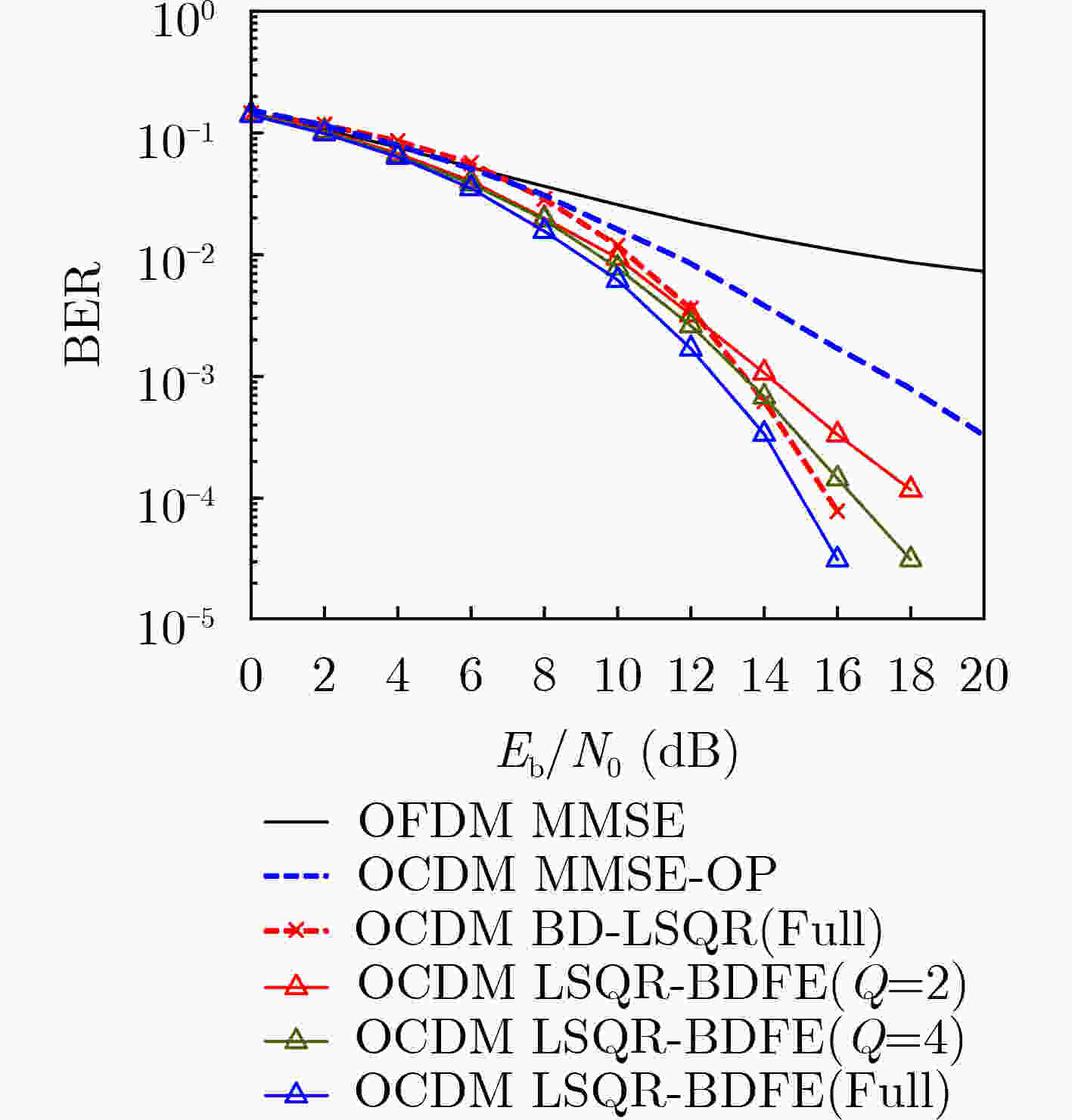
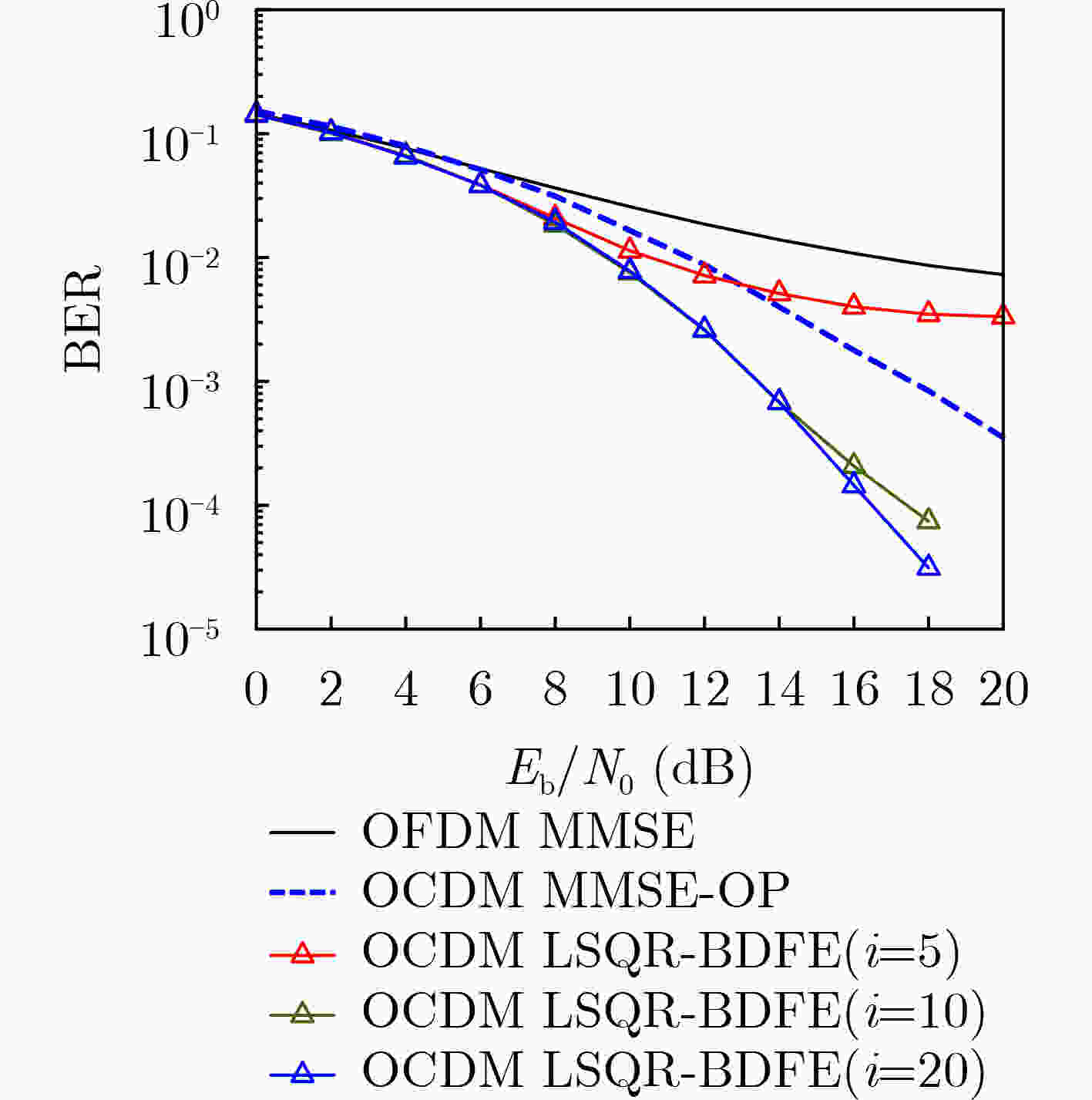
摘要: 正交Chirp复用(OCDM)是近年来提出的一种新的多载波体系,通过菲涅尔变换,获得一组正交Chirp信号,实现了CSS的最大频谱效率。该文介绍了OCDM系统的基本原理,重点研究了OCDM系统的低复杂度均衡算法。双选信道下,传统的MMSE均衡算法性能下降,提出一种基于近似带状矩阵的阻尼LSQR算法,作为求解稀疏矩阵的最小二乘迭代算法。为了缓解快速时变信道中的ICI,提出一种基于近似带状矩阵的LSQR-BDFE算法,结合判决反馈均衡,通过LSQR算法迭代计算。仿真结果表明,双选信道下,OCDM系统比OFDM系统有着更好的BER性能,所提出的LSQR-BDFE算法和带状阻尼LSQR算法,比MMSE均衡算法有着性能优势。
-
关键词:
- 正交Chirp复用(OCDM) /
- 菲涅尔变换 /
- 带状阻尼LSQR算法 /
- LSQR-BDFE算法
Abstract: Orthogonal Chirp Division Multiplexing(OCDM) is a new multi-carrier system proposed in recent years. Through Fresnel transform, a set of orthogonal Chirp signals are obtained, which achieve the maximum spectral efficiency of CSS. In this paper, the basic principle of OCDM systems is introduced and the low complexity equalization algorithm of OCDM systems is studied. In doubly-selective channels, the performance of the traditional MMSE equalization algorithm declines. A Damped-LSQR algorithm is proposed based on approximate banded matrix, as a least square iterative algorithm for sparse matrix. To alleviate ICI in rapidly time-varying channels, an LSQR-BDFE algorithm is proposed based on approximate banded matrix. Combined with decision feedback equalization, LSQR algorithm is used for iterative calculation. The simulation results show that the OCDM system has better BER performance than the OFDM system under doubly-selective channels. The LSQR-BDFE algorithm and Band Damped-LSQR algorithm have performance advantages compared with the MMSE equalization algorithm. -
表 1 3种均衡算法的计算复杂度
算法 复杂度 MMSE-OP(A) $ N + 2N{\log _2}N $ BD-LSQR(B) $ NQ + \left( {i + 2} \right)N{\log _2}N $ LSQR-BDFE(C) $ N{Q^2} + \left( {i + 2} \right)N{\log _2}N $ -
[1] OMAR M S and MA Xiaoli. Spectrum design for orthogonal chirp division multiplexing transmissions[J]. IEEE Wireless Communications Letters, 2020, 9(11): 1990–1994. doi: 10.1109/LWC.2020.3010774 [2] COOPER K B, DENGLER R J, LLOMBART N, et al. THz Imaging Radar for Standoff Personnel Screening[J]. IEEE Transactions on Terahertz Science and Technology, 2011, 1(1): 169–182. doi: 10.1109/TTHZ.2011.2159556 [3] KIM J H, YOUNIS M, MOREIRA A, et al. A novel OFDM chirp waveform scheme for use of multiple transmitters in SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 568–572. doi: 10.1109/LGRS.2012.2213577 [4] OUYANG Xing and ZHAO Jian. Orthogonal chirp division multiplexing[J]. IEEE Transactions on Communications, 2016, 64(9): 3946–3957. doi: 10.1109/TCOMM.2016.2594792 [5] 吕鑫. OCDM-OFDM雷达通信一体化信号设计与研究[D]. [硕士论文], 南京理工大学, 2019.LV Xin. Design and research of OCDM-OFDM radar communication integrated signal[D]. [Master dissertation], Nanjing University of Science and Technology, 2019. [6] ZHU Peibin, XU Xiaomei, TU Xingbin, et al. Anti-multipath orthogonal chirp division multiplexing for underwater acoustic communication[J]. IEEE Access, 2020, 8: 13305–13314. doi: 10.1109/ACCESS.2020.2966072 [7] BOUVET P J, AUFFRET Y, and AUBRY C. On the analysis of orthogonal chirp division multiplexing for shallow water underwater acoustic communication[C]. Proceedings of OCEANS 2017-Aberdeen, Aberdeen, UK, 2017: 1–5. [8] WANG Xin, JIANG Zhe, and SHEN Xiaohong. Low complexity equalization of orthogonal chirp division multiplexing in doubly-selective channels[J]. Sensors, 2020, 20(11): 3125. doi: 10.3390/s20113125 [9] RUGINI L, BANELLI P, and LEUS G. Low-complexity banded equalizers for OFDM systems in doppler spread channels[J]. EURASIP Journal on Advances in Signal Processing, 2006, 2006: 067404. doi: 10.1155/ASP/2006/67404 [10] OUYANG Xing and ZHAO Jian. Orthogonal chirp division multiplexing for coherent optical fiber communications[J]. Journal of Lightwave Technology, 2016, 34(18): 4376–4386. doi: 10.1109/JLT.2016.2598575 [11] MARTONE M. A multicarrier system based on the fractional fourier transform for time-frequency-selective channels[J]. IEEE Transactions on Communications, 2001, 49(6): 1011–1020. doi: 10.1109/26.930631 [12] 陈恩庆, 陶然, 张卫强, 等. 一种基于分数阶傅里叶变换的OFDM系统及其均衡算法[J]. 电子学报, 2007, 35(3): 409–414. doi: 10.3321/j.issn:0372-2112.2007.03.005CHEN Enqing, TAO Ran, ZHANG Weiqiang, et al. The OFDM system and equalization algorithm based on the fractional Fourier transform[J]. Acta Electronica Sinica, 2007, 35(3): 409–414. doi: 10.3321/j.issn:0372-2112.2007.03.005 [13] YIN Yufang. The CPDA detector for the MIMO OCDM system[C]. Proceedings of the 2021 IEEE 6th International Conference on Computer and Communication Systems, Chengdu, China, 2021: 1001–1004. [14] ASIF A and MOURA J M F. Block matrices with L-block-banded inverse: Inversion algorithms[J]. IEEE Transactions on Signal Processing, 2005, 53(2): 630–642. doi: 10.1109/TSP.2004.840709 [15] FANG Kun, RUGINI L, and LEUS G. Low-complexity block turbo equalization for OFDM systems in time-varying channels[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5555–5566. doi: 10.1109/TSP.2008.929129 [16] 赵晓君, 曹琲琲. OFDM系统下基于阻尼LSQR的低复杂度检测算法研究[J]. 移动通信, 2017, 41(16): 75–80. doi: 10.3969/j.issn.1006-1010.2017.16.015ZHAO Xiaojun and CAO Feifei. Research on low-complexity detection algorithm based on damped LSQR in OFDM system[J]. Mobile Communications, 2017, 41(16): 75–80. doi: 10.3969/j.issn.1006-1010.2017.16.015 [17] HAN Hua and WU Lenan. Low complexity LSQR-based block decision feedback equalizer for OFDM systems over rapidly time-varying channels[C]. Proceedings of 2010 International Conference on Communications and Mobile Computing, Shenzhen, China, 2010: 438–441. [18] SCHNITER P. Low-complexity equalization of OFDM in doubly selective channels[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 1002–1011. doi: 10.1109/TSP.2004.823503 [19] RUGINI L, BANELLI P, and LEUS G. Simple equalization of time-varying channels for OFDM[J]. IEEE Communications Letters, 2005, 9(7): 619–621. doi: 10.1109/LCOMM.2005.1461683 [20] HRYCAK T, DAS S, MATZ G, et al. Low complexity equalization for doubly selective channels modeled by a basis expansion[J]. IEEE Transactions on Signal Processing, 2010, 58(11): 5706–5719. doi: 10.1109/TSP.2010.2063426 -





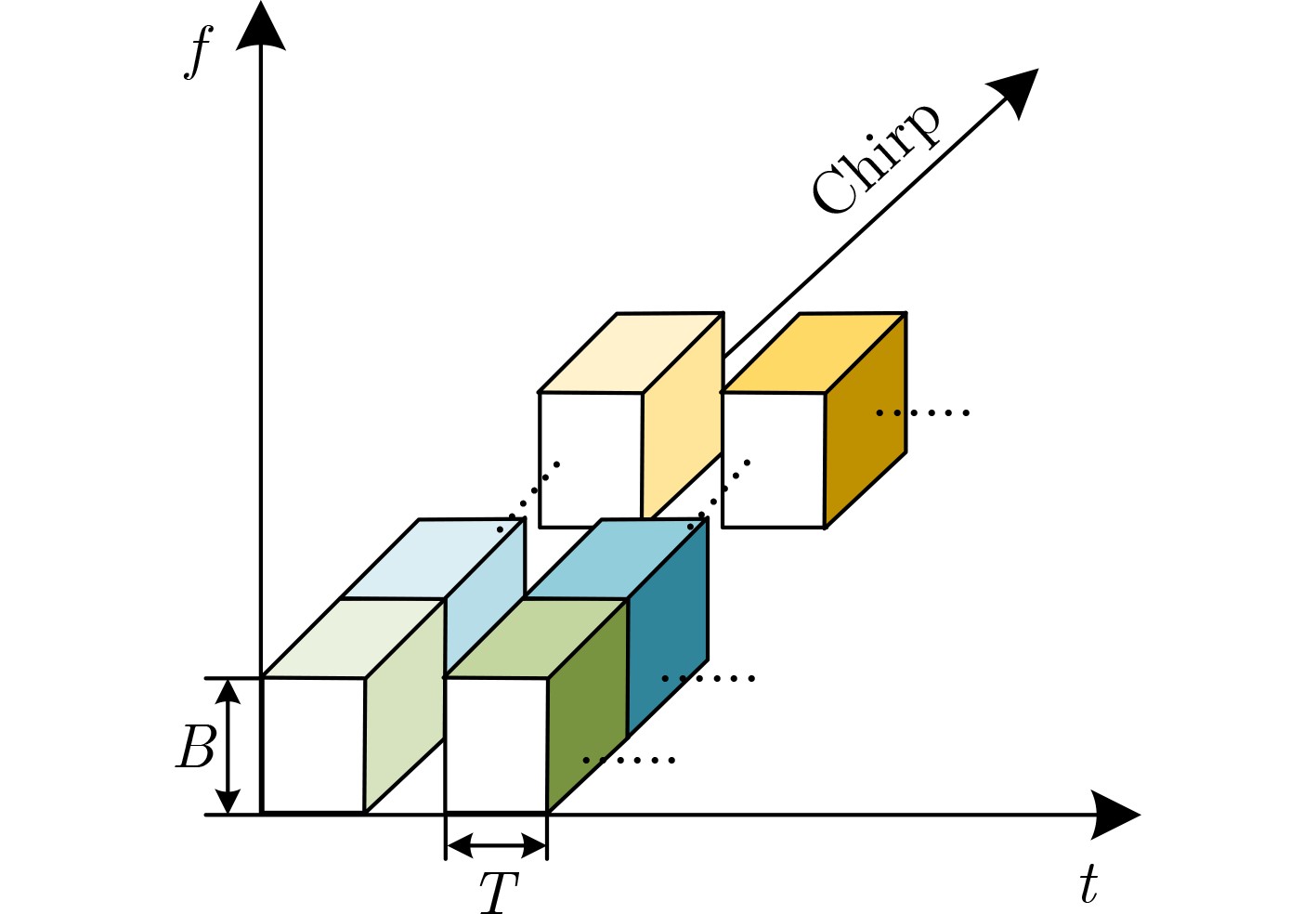
 下载:
下载:
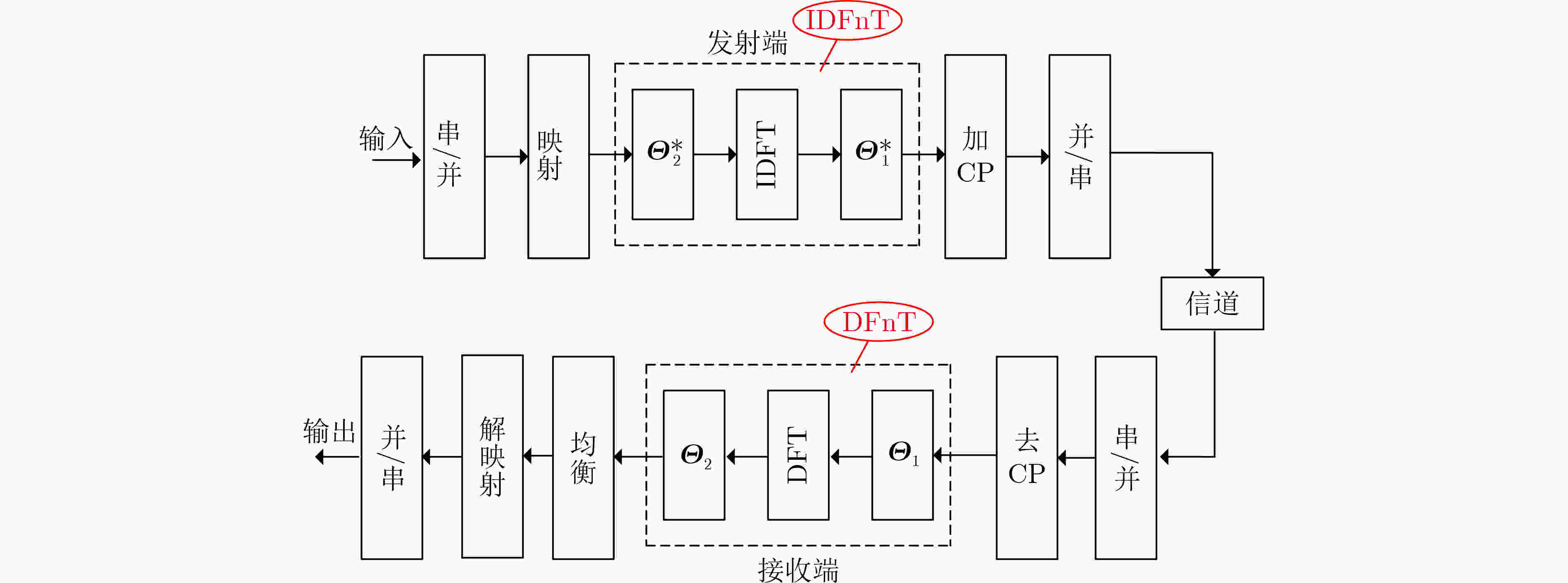
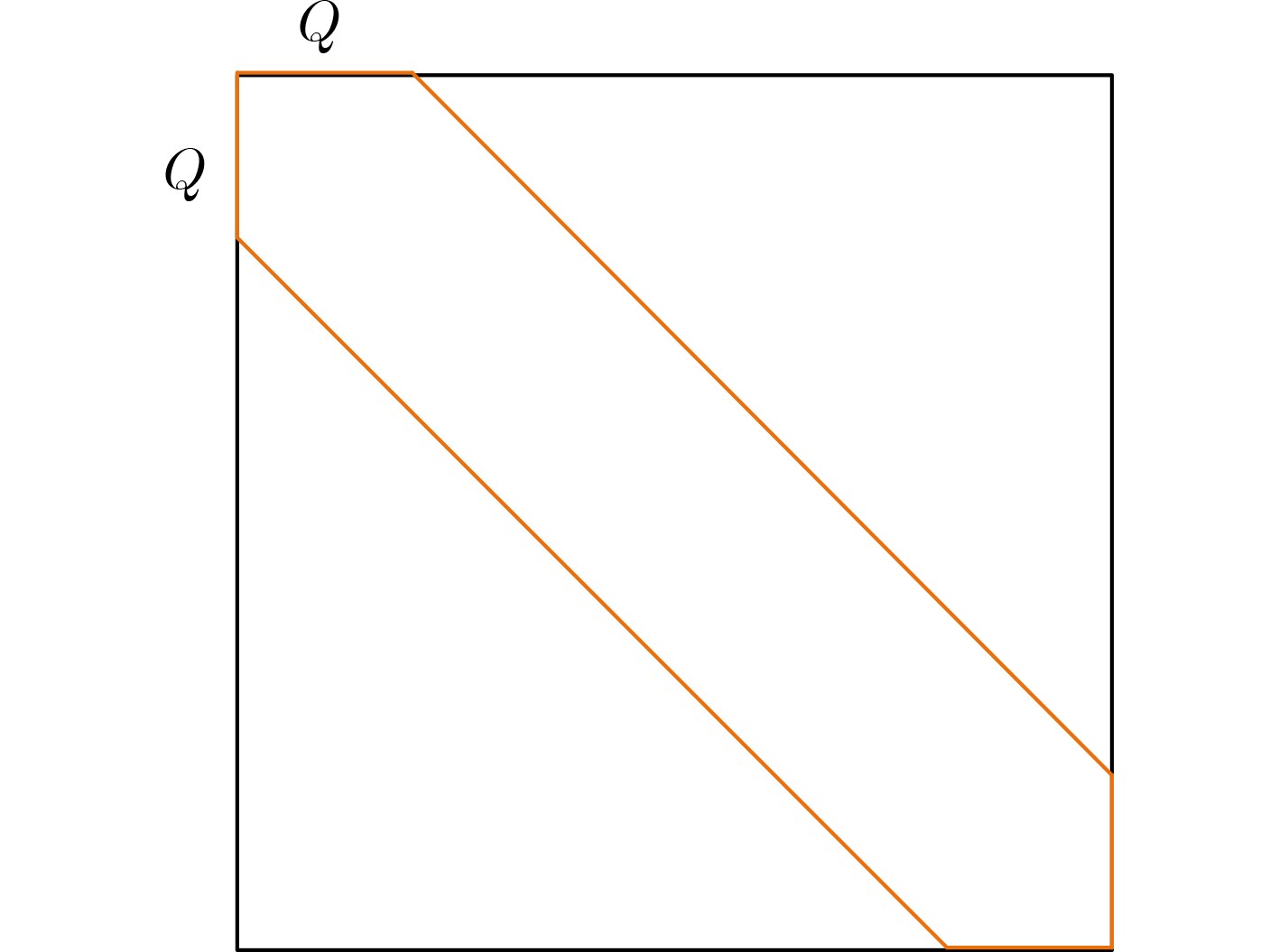
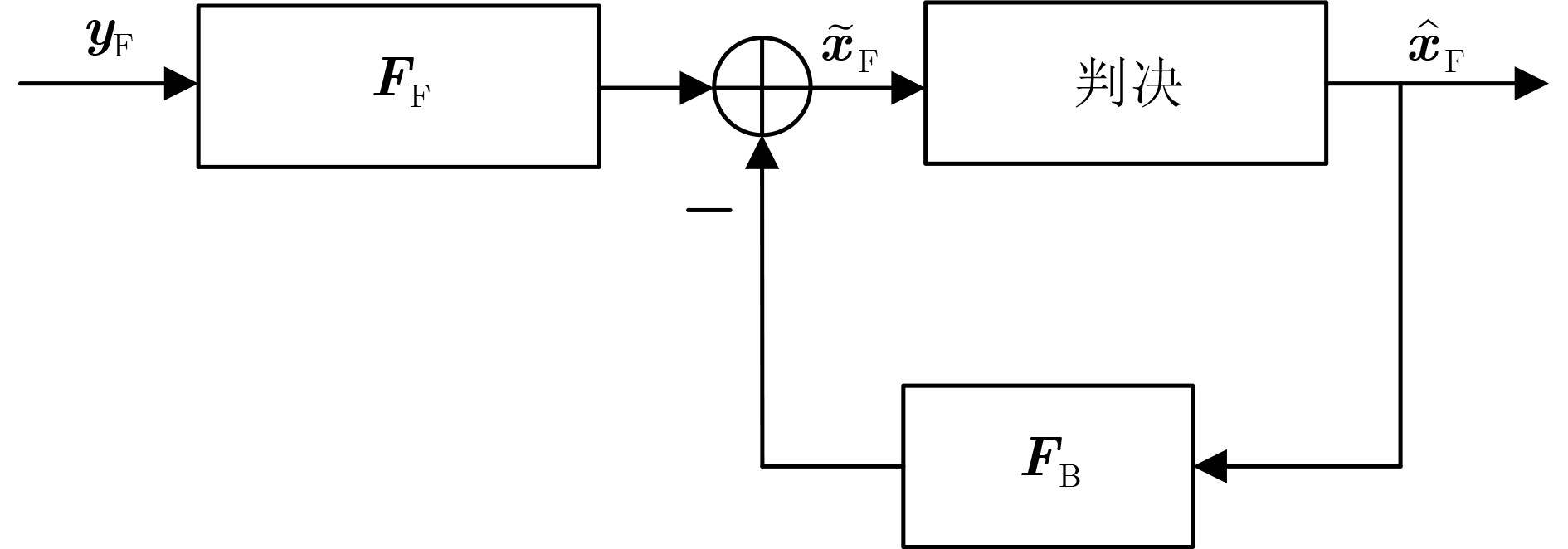




 下载:
下载:
