Distributed Direct Position Determination Technology Based on VEPPSO-EXTRA Hybrid Algorithm
-
摘要: 相对于集中式直接定位技术,分布式直接定位算法具有计算复杂度小和通信代价小等优点,但存在定位精度损失的问题。针对于此,该文提出一种基于VEPPSO-EXTRA混合算法的分布式直接定位技术。首先,基于子空间融合的直接定位算法,推导其分布式优化的数学模型;其次,基于多种群联合进化的思想,提出一种基于向量评估的并行粒子群算法(VEPPSO)实现全局寻优,由此得到辐射源迭代初始值;最后,引入分布式精确一阶算法(EXTRA)求解最终位置以降低分布式计算带来的精度损失。实验结果表明,相较于现有的分布式直接定位算法,该技术能解决定位精度损失的问题,且其计算复杂度与通信代价低于对应的集中式直接定位算法。
-
关键词:
- 分布式直接定位 /
- 传感器网络 /
- 基于向量评估的并行粒子群算法 /
- 精确1阶算法
Abstract: Compared with centralized direct position determination, distributed direct position determination algorithm has the advantages of low computational complexity and low communication cost, but it has the problem of location accuracy loss. This paper proposes a distributed direct position determination technique based on the VEPPSO-EXTRA hybrid algorithm. Firstly, based on the direct position determination algorithm of subspace fusion, a distributed optimization model is derived; Secondly, based on the idea of multi-population joint evolution, a Vector Evaluation based Parallel Particle Swarm Optimization (VEPPSO) algorithm is proposed to achieve global optimization, and the initial value of the emitter iteration is obtained; Finally, the distributed Exact First-Order Algorithnm (EXTRA) is introduced to solve the final position to reduce the accuracy loss caused by distributed computing. The experimental results show that compared with the existing distributed direct position determination algorithm, this technology can solve the problem of location accuracy loss, and its computational complexity and communication cost are lower than the corresponding centralized direct position determination algorithm. -
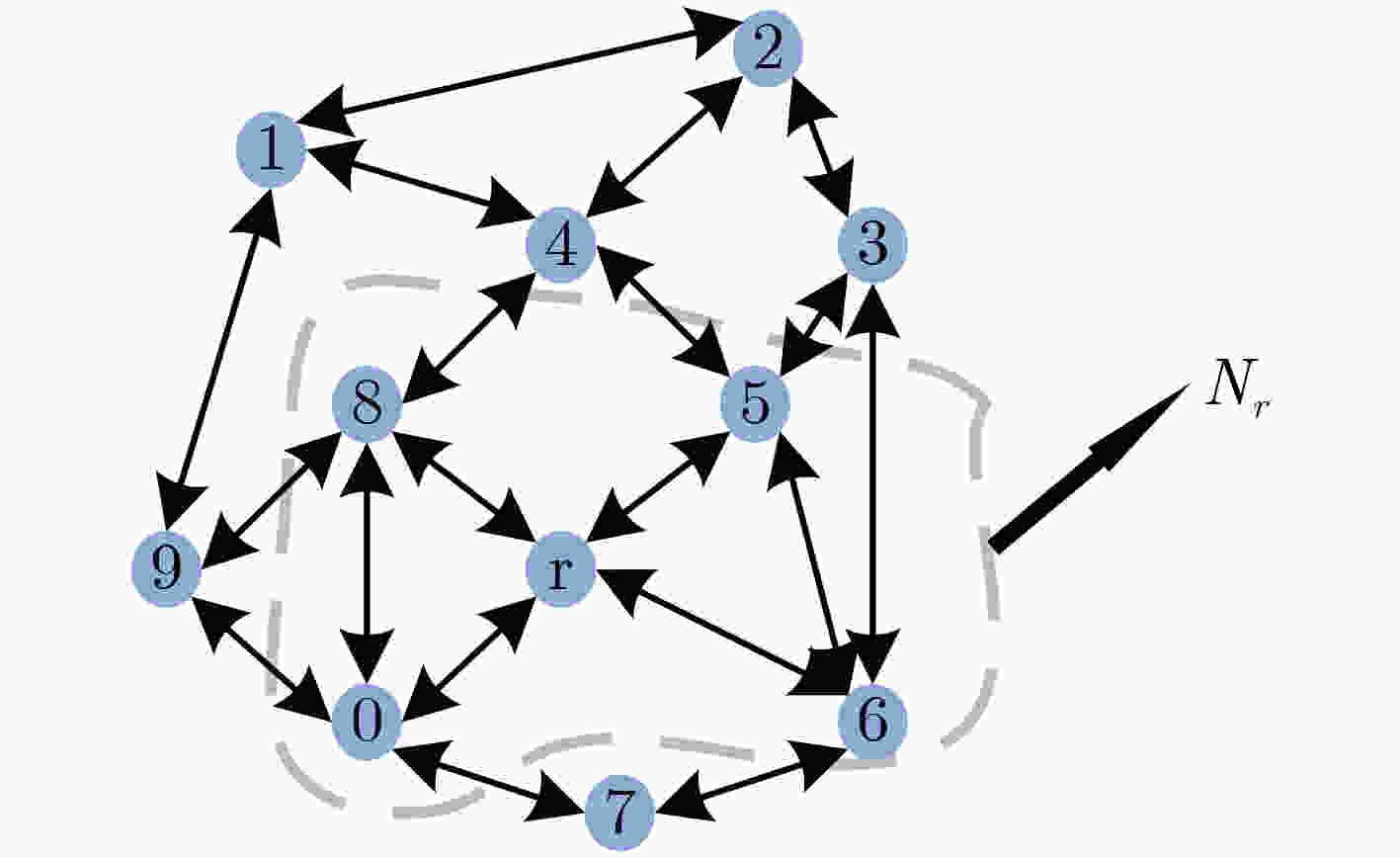
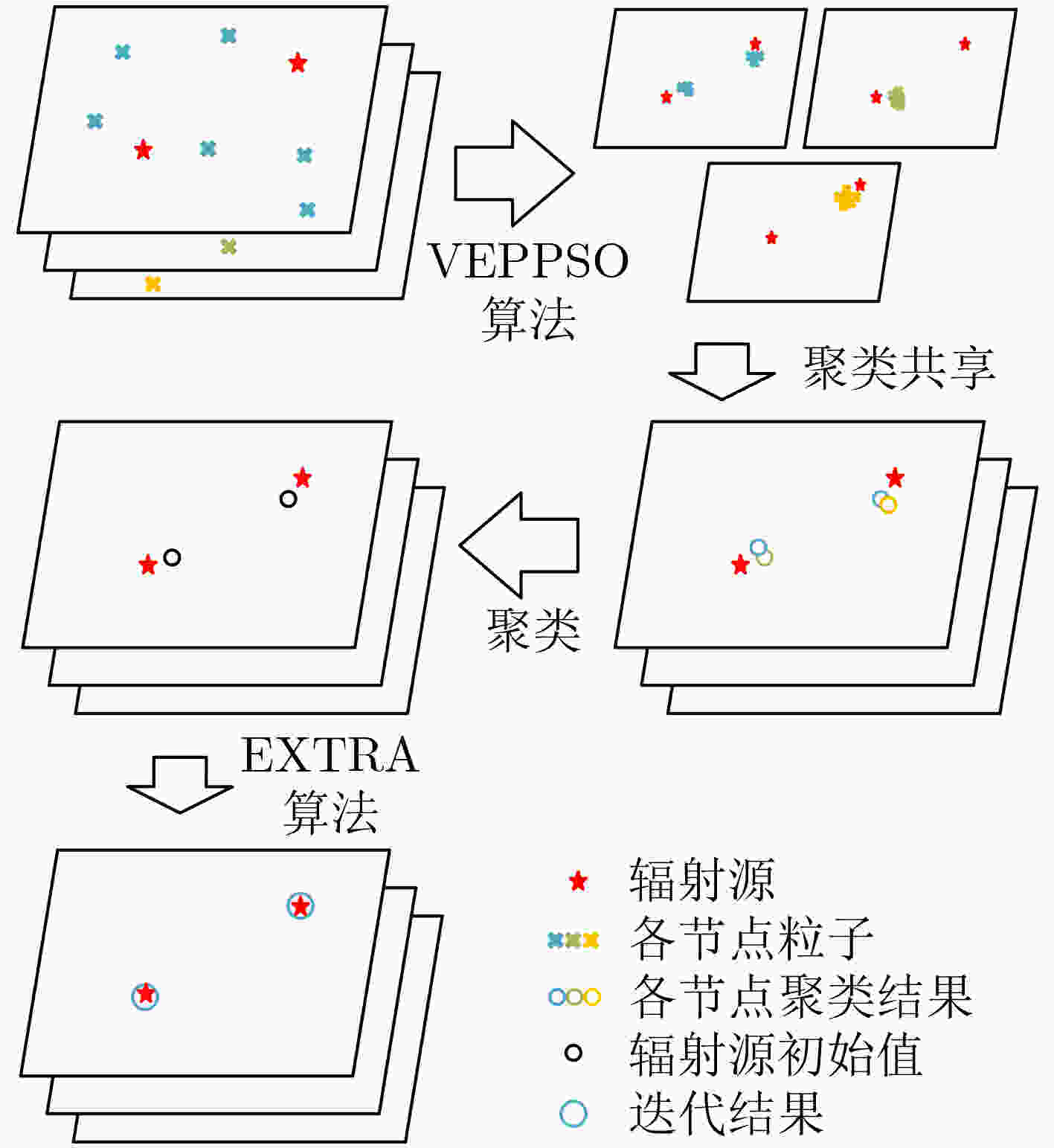
算法1 VEPPSO-EXTRA算法 输入:初始化VEPPSO算法的各节点粒子数$ {N_{\text{p}}} $,粒子群迭代次数$ {N_{{\text{iter1}}}} $,EXTRA算法合适的步长$ \alpha $,混合加权矩阵${\boldsymbol{A}} = [{a_{r,l} }] \in {\mathbb{R}^{R \times R} }$。 (1)VEPPSO算法及聚类优化 (a)通过局部代价函数式(10),评估粒子状态。如果$ {J'_r}({\text{xo}}{{\text{y}}_i}) < {J'_r}({{\boldsymbol{p}}_i}) $,$ {{\boldsymbol{p}}_i} = {\text{xo}}{{\text{y}}_i} $,如果$ {J'_r}({{\boldsymbol{p}}_i}) < {J'_r}({{\boldsymbol{p}}_{g[r]}}) $,$ {{\boldsymbol{p}}_{g[r]}} = {{\boldsymbol{p}}_i} $; (b)交换粒子之间和种群之间的信息。$ {{\boldsymbol{p}}_{{\text{local\_i}}}} = $相邻粒子最优状态$ ({{\boldsymbol{p}}_{i - 1}},{{\boldsymbol{p}}_i},{{\boldsymbol{p}}_{i{\text{ + 1}}}}) $,$ {{\boldsymbol{p}}_{g[{{\boldsymbol{N}}_r}]}} = $相邻粒子群随机状态$ ({{\boldsymbol{p}}_{g[l]}}),l \in {{\boldsymbol{N}}_r} $; (c)对于每个种群$ r $并行执行式(14)和式(15),实现位置更新,如果迭代未结束,跳转到(a); (d)当$ n = {N_{{\text{iter1}}}} $时结束迭代,并将各个种群的粒子的历史最优位置$ {{\boldsymbol{p}}_i} $作为辐射源位置初始值的估计结果; (e)将各种群估计结果经聚类后分享到各邻居节点,然后再次通过传统聚类优化算法得到辐射源迭代初始值$ {{\boldsymbol{p}}_{r,1}} $。 (2)EXTRA算法 (a)每个节点进行初始化,$ {{\boldsymbol{p}}_{r,2}} = \displaystyle\sum\limits_{l \in {{\boldsymbol{N}}_r}} {{a_{r,l}}{{\boldsymbol{p}}_{l,1}}} - \alpha \nabla J'({{\boldsymbol{p}}_{r,1}}) $; (b)每个节点并行迭代,$ {{\boldsymbol{p}}_{r,i + 2}} = \displaystyle\sum\limits_{l \in {{\boldsymbol{N}}_r}} {{a_{r,l}}{{\boldsymbol{p}}_{l,i + 1}}} - \left(\displaystyle\sum\limits_{l \in {{\boldsymbol{N}}_r}} {\frac{{{a_{r,l}}}}{2}{{\boldsymbol{p}}_{r,i}}} + \frac{{{{\boldsymbol{p}}_{r,i}}}}{2}\right) - \alpha [\nabla J'({{\boldsymbol{p}}_{r,i + 1}}) - \nabla J'({{\boldsymbol{p}}_{r,i}})] $,直至定位结果迭代误差小
于设定值。输出:辐射源位置最终估计$ {\boldsymbol{p}} $。 表 2 算法执行时间(s)
算法 总时长 平均时长 集中式直接定位算法 1.2658 – 本文分布式直接定位算法 6.3000 0.3150 -
[1] 刘聪锋. 无源定位与跟踪[M]. 西安: 西安电子科技大学出版社, 2011: 1–4.LIU Congfeng. Passive Location and Tracking[M]. Xi'an: Xidian University Press, 2011: 1–4. [2] TZOREFF E and WEISS A J. Expectation-maximization algorithm for direct position determination[J]. Signal Processing, 2017, 133: 32–39. doi: 10.1016/j.sigpro.2016.10.015 [3] LI Jianfeng, HE Yi, ZHANG Xiaofei, et al. Simultaneous localization of multiple unknown emitters based on UAV monitoring big data[J]. IEEE Transactions on Industrial Informatics, 2021, 17(9): 6303–6313. doi: 10.1109/TII.2020.3048987 [4] WU Guizhou, ZHANG Min, GUO Fucheng, et al. Direct position determination of coherent pulse trains based on Doppler and Doppler rate[J]. Electronics, 2018, 7(10): 262. doi: 10.3390/electronics7100262 [5] 吴癸周, 郭福成, 张敏. 信号直接定位技术综述[J]. 雷达学报, 2020, 9(6): 998–1013. doi: 10.12000/JR20040WU Guizhou, GUO Fucheng, and ZHANG Min. Direct position determination: An overview[J]. Journal of Radars, 2020, 9(6): 998–1013. doi: 10.12000/JR20040 [6] NEDIĆ A, OLSHEVSKY A, and RABBAT M G. Network topology and communication-computation tradeoffs in decentralized optimization[J]. Proceedings of the IEEE, 2018, 106(5): 953–976. doi: 10.1109/JPROC.2018.2817461 [7] POURHOMAYOUN M and FOWLER M L. Distributed computation for direct position determination emitter location[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 2878–2889. doi: 10.1109/TAES.2014.130005 [8] 朱颖童, 董春曦, 董阳阳, 等. 去中心化时差频差直接定位方法[J]. 航空学报, 2017, 38(5): 320727. doi: 10.7527/S1000-6893.2016.320727ZHU Yingtong, DONG Chunxi, DONG Yangyang, et al. Decentralized direct position determination method based on TDOA and FDOA[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(5): 320727. doi: 10.7527/S1000-6893.2016.320727 [9] MA Fuhe, LIU Zhangmeng, and GUO Fucheng. Distributed direct position determination[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 14007–14012. doi: 10.1109/TVT.2020.3025386 [10] XIA Wei and LIU Wei. Distributed adaptive direct position determination of emitters in sensor networks[J]. Signal Processing, 2016, 123: 100–111. doi: 10.1016/j.sigpro.2016.01.002 [11] DEMISSIE B, OISPUU M, and RUTHOTTO E. Localization of multiple sources with a moving array using subspace data fusion[C]. Proceedings of the 11th International Conference on Information Fusion, Cologne, Germany, 2008: 1–7. [12] LI Xiaodong. Erratum to “niching without niching parameters: Particle swarm optimization using a ring topology” [Feb 10 150-169][J]. IEEE Transactions on Evolutionary Computation, 2010, 14(4): 665. doi: 10.1109/TEVC.2010.2050024 [13] SHI Wei, LING Qing, WU Gang, et al. EXTRA: An exact first-order algorithm for decentralized consensus optimization[J]. SIAM Journal on Optimization, 2015, 25(2): 944–966. doi: 10.1137/14096668X [14] WU Guizhou, ZHANG Min, and GUO Fucehng. High-resolution direct position determination based on eigenspace using a single moving ULA[J]. Signal, Image and Video Processing, 2019, 13(5): 887–894. doi: 10.1007/s11760-019-01425-4 [15] PARSOPOULOS K E, TASOULIS D K, and VRAHATIS M N. Multiobjective optimization using parallel vector evaluated particle swarm optimization[C]. Proceedings of the IASTED International Conference on Artificial Intelligence and Applications (AIA 2004), Innsbruck, Austria, 2004: 823–828. -





 下载:
下载:


 下载:
下载:
