A New Key Pre-distribution Scheme from Symplectic Spaces
-
摘要: 密钥预分配是无线传感器网络中最具挑战的安全问题之一。 该文基于有限域上辛空间中子空间之间的正交关系构造了一个新的组合设计,并基于该设计构造了一个密钥预分配方案。令V 是有限域上8维辛空间中的一个(4,2)型子空间,V 中每一个(1,0)型子空间看作密钥预分配方案中的一个节点,所有的(2,1)型子空间看作该方案的一个密钥池。将整个目标区域划分为若干个大小相同的小区,每个小区有普通节点和簇头两种类型的传感器节点。小区内的普通节点采用基于辛空间的密钥预分配方案分发密钥,不同小区内节点所用密钥池互不相同,因此不同小区内的节点需通过簇头建立间接通信,不同小区内簇头采用完全密钥预分配方式分发密钥。与其他方案相比,该方案的最大优势是网络中节点的抗捕获能力较强,且随着网络规模的不断扩大,网络的连通概率逐渐趋于1。Abstract: Key pre-distribution is one of the most challenging security problems in wireless sensor networks. In the paper, a new combinatorial design based on the orthogonal relation between the subspaces of symplectic space over finite fields is constructed, and a key pre-distribution scheme is constructed from the design. Let V be a subspace of type (4,2) in an 8-dimensional symplectic space over finite fields. A subspace of type (1,0) in V is regarded as a node in the key pre-distribution scheme, and all the subspaces of (2,1) in V is regarded as the key pool of the scheme. The whole target area is divided into a number of equally sized cells, each cell has normal nodes and cluster heads two types nodes. The key pre-distribution scheme from symplectic space is adopted to distribute keys to nodes of each cell, and different cells has different key pools, so nodes in different cells need to establish indirect communication through the cluster heads, the cluster heads in different cells distribute keys in a complete key pre-distribution scheme. Compared with other schemes, the advantages of the proposed scheme is the strong anti-compromise ability of nodes in the networks, and with the continuous expansion of the network scale, the connectivity gradually tends to 1.
-
Key words:
- Wireless sensor network /
- Key pre-distribution /
- Combinatorial design /
- Symplectic space
-
表 1 部分平衡
$ 2 - ({q^4} + {q^2},{q^2};1,0) $ 设计到密钥预分配方案的对应关系部分平衡$ 2 - ({q^4} + {q^2},{q^2};1,0) $区组设计 密钥预分配方案 $ v = |X| = N(2,1;4) = {q^4} + {q^2} $ 密钥池大小 $ b = |\mathcal{B}| = N(1,0;4) = {q^3} + {q^2} + q + 1 $ 方案所能支持的最大传感器节点数目 $ k = |X(B)| = N(2,1;3,1;4) = {q^2} $ 密钥环大小 $ r = |\mathcal{B}(x)| = N(1,0;2,1;4) = q + 1 $ 包含一给定密钥的节点数目 $ \delta = 0 $或$ 1 $ 任意两个节点共享的密钥量 表 2 当
$ q = 4 $ ,$ q = 5 $ ,$ q = 7 $ ,$ q = 8 $ 时的局部损失概率$ q $ $ N $ $ b $ $ k $ $ S $ ${\rm{fail}}(1)$ ${\rm{fail}}(s)$ 4 400 85 16 500 0.0361 0.0449 4 400 85 16 600 0.0361 0.0537 5 900 156 25 1200 0.0260 0.0345 7 1300 400 49 1800 0.0151 0.0208 8 1600 585 64 2200 0.0120 0.0165 表 3 各个方案的参数
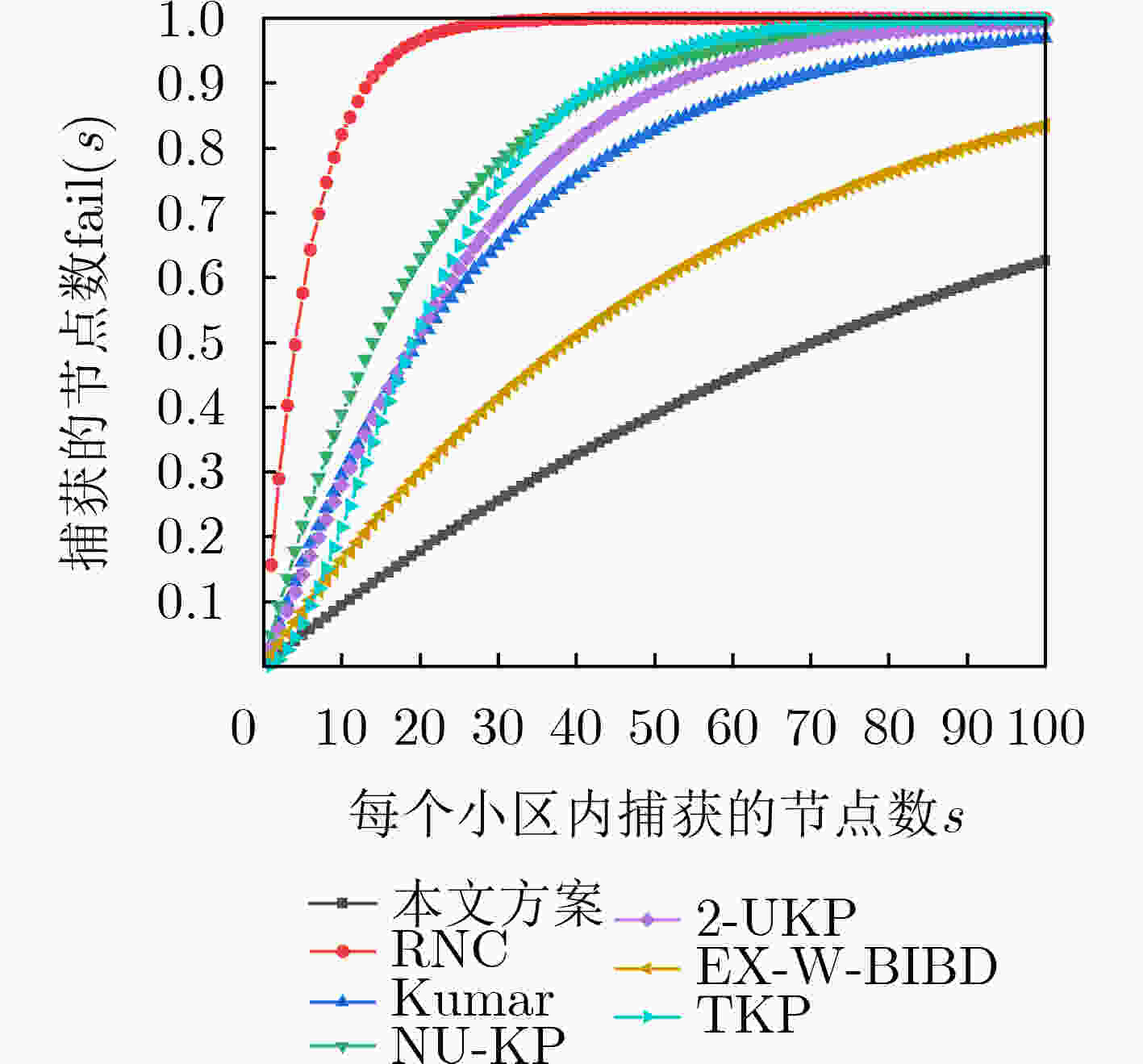
方案 $ v $ $ b $ $ k $ $ p $ $ {\rm{fail}}(s) $ RNC $ {q^2}{\text{ + }}q + 1 $ $ {q^5} - {q^2} $ $ q + 1 $ $ {\mu _c}/(b - 1) $ $ 1 - {(1 - {\rm{fail}}(1))^s} $ NU-KP $ {q^3} + 1 $ $ {q^4} - {q^3} + {q^2} $ $ q + 1 $ $ {(q + 1)^2}/({q^3} + q + 1) $ $ 1 - C_{b - {q^2}}^s/C_b^s $ 2-UKP $ {q^3} + 1 $ ${b'}$ $ 2(q + 1) $ $ 1 - {(1 - {(q + 1)^2}/(v + q))^4} $ $ \displaystyle\sum\nolimits_{i = 1}^4 {{{(1 - u)}^i}p(i)/p} $ Kumar’s $ {q^2}{\text{ + }}q + 1 $ $ {q^2}{\text{ + }}q + 1 $ $ q + 1 $ $ 1 $ $ 1 - {(1 - (q - 1)/b)^s} $ TKP $ {q^2} - q $ $ 2{q^2} $ $ 2(q+1) $ $ ({k^2} - k)/(4{q^2} - 2) $ $ 1 - (C_t^s + 4C_t^{s - 1}(q - 1))/C_b^s $ Ex-w-BIBD $ 8{q^3} $ $ 8{q^3} $ $ 6q - 3 $ $ 6q/(4{q^2} + 2q + 1) $ $ p_1' r_1'(s){\text{ + }}p_2' r_2'(s) $ 本文 $ {q^4}{\text{ + }}{q^2} $ $ {q^3}{\text{ + }}{q^2}{\text{ + }}q + 1 $ $ {q^2} $ $ {q^3}/(b - 1) $ $ 1 - {(1 - (q - 1)/(b - 2))^s} $ 注:(1)${\mu _c} = \sum\limits_{s = 1}^{t - 1} {C_k^s} \mu' _c(s)$, $\mu' _c(s) = {\lambda _s} - 1 - \sum\limits_{i = 1}^{t - 1 - s} {C_{k - s}^i} \mu _c'(s + i)$, ${\rm{fail}}(1) = (\sum\limits_{s = 1}^{t - 1} {C_k^s{\lambda _s}\mu '_c(s)} )/(b\sum\limits_{s = 1}^{t - 1} {C_k^s\mu '_c(s)} )$。
(2)$ {q^4} - 2{q^3} + q \le 2{b'} \le{q^4} - {q^3} + {q^2} , u = C_{{q^4} - {q^3}}^{2s}/C_{{q^4} - {q^3} + {q^2}}^{2s} , p(i) = C_4^i{d^i} \times {(1 - d)^{4 - i}} , p{\text{ = }}1 - {(1 - d)^4} $。
(3) ${p'_1} = 6q/(4{q^2} + 2q + 1) , r'_1(s) = 1 - 2{(1 - (6q - 5)/(8{q^3} - 2))^s} + {(1 - (12q - 10)/(8{q^3} - 2))^s} , {p_2}{'{ = 3/(4} }{ { {q} }^2}{ { + 2q + 1)} }$, ${r}'_{2}(s){ {=s} '_{22} }(s)/{C}_{s}^{8{q}^{2}-4{\rm{q}}} , t = 2{q^2} - 4q + 2 , { {s} }'_{22}(s){ {=C} }_{s}^{4q(2q-1)}-{C}_{1}^{2q-2}{C}_{s}^{2(2q-1)(2q-1)}+{C}_{2}^{2q-2}{C}_{s}^{2(2q-1)(2q-2)}+\cdots +{(-1)}^{\theta }{C}_{\theta }^{2q-2}{C}_{s}^{2(2q-1)(2q-\theta )}$。表 4 符号表
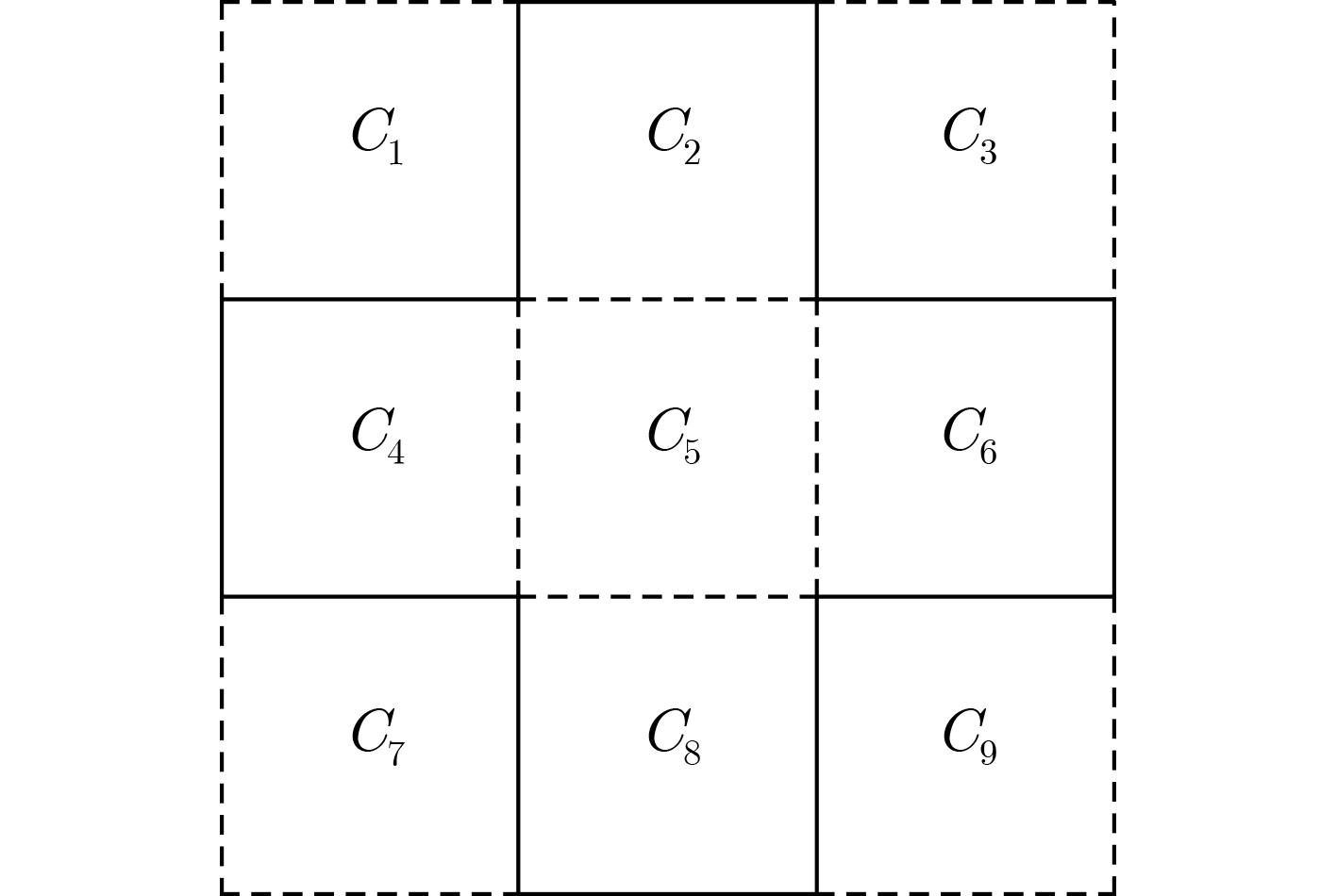
符号 符号说明 符号 符号说明 $ X $($ |X| = v $) 点集(点集的大小/密钥池的大小) $ {C_i} $ 网络中第$ i $个小区 $ \mathcal{B} $($ |\mathcal{B}| = b $) 区组集(区组数目/方案所支持的最大传感器节点数目) ${{\rm{CH}}_{ij} }$ 网络中第$ i $个小区中的$ j $类型簇头 $ k $ 每个区组的大小(每个节点所含的密钥量) $ p $ 网络的连通概率 $ r $ 包含一给定点的区组数(包含一给定密钥的节点数目) ${\rm{fail}}(s)$ $ s $个节点被捕获时网络的损失概率 -
[1] 赵金兰, 李娅, 岳庆玲, 等. 无线传感器网络技术的应用及前景分析[J]. 江苏科技信息, 2021, 38(35): 51–53.ZHAO Jinlan, LI Ya, YUE Qingling, et al. Application and prospect analysis of wireless sensor network technology[J]. Jiangsu Science &Technology Information, 2021, 38(35): 51–53. [2] CAMTEPE S A and YENER B. Combinatorial design of key distribution mechanisms for wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2007, 15(2): 346–358. doi: 10.1109/TNET.2007.892879 [3] PEI Dingyi, DOND Junwu, and RONG Chunming. A novel key pre-distribution scheme for wireless distributed sensor networks[J]. Science China Information Sciences, 2010, 53(2): 288–298. doi: 10.1007/s11432-010-0005-0 [4] BAG S. A new key predistribution scheme for grid-group deployment of wireless sensor networks[J]. Ad Hoc & Sensor Wireless Networks, 2015, 27(3/4): 313–329. [5] CHEN Shangdi and WEN Jiejing. New key pre-distribution scheme using symplectic geometry over finite fields for wireless sensor networks[J]. The Journal of China Universities of Posts and Telecommunications, 2017, 24(5): 16–22,76. doi: 10.1016/S1005-8885(17)60229-2 [6] KUMAR A and PAIS A R. A new combinatorial design based key pre-distribution scheme for wireless sensor networks[J]. Journal of Ambient Intelligence and Humanized Computing, 2019, 10(6): 2401–2416. doi: 10.1007/s12652-018-0902-4 [7] AKHBARIFAR S, JAVADI H H S, RAHMANI A M, et al. Hybrid key pre-distribution scheme based on symmetric design[J]. Iranian Journal of Science and Technology, Transactions A:Science, 2019, 43(5): 2399–2406. doi: 10.1007/s40995-019-00703-7 [8] 袁琪, 马春光, 姚建盛, 等. 基于w-BIBD的异构传感网密钥预分配方案[J]. 浙江大学学报:工学版, 2019, 53(1): 126–136. doi: 10.3785/j.issn.1008-973X.2019.01.014YUAN Qi, MA Chunguang, YAO Jiansheng, et al. w-balanced incomplete block design method for key pre-distribu-tion scheme in heterogeneous wireless sensor network[J]. Journal of Zhejiang University:Engineering Science, 2019, 53(1): 126–136. doi: 10.3785/j.issn.1008-973X.2019.01.014 [9] PANG Shanqi, LI Yongmei, GAO Qiang, et al. Key predistribution schemes based on orthogonal arrays with unique hamming distance distribution[J]. Wireless Personal Communications, 2020, 112(3): 1919–1945. doi: 10.1007/s11277-020-07133-4 [10] PANG Shanqi, HU Xianchao, GAO Qiang, et al. Accurate analysis of connectivity and resilience for a class of wireless sensor networks[J]. Chinese Journal of Electronics, 2020, 29(2): 208–219. doi: 10.1049/cje.2019.12.007 [11] CHOUDHARY V and TARUNA S. The highly secure polynomial pool-based key pre-distribution scheme for wireless sensor network[J]. Journal of Discrete Mathematical Sciences and Cryptography, 2020, 23(1): 95–114. doi: 10.1080/09720529.2020.1721880 [12] BELIM S V and BELIM S Y. A general scheme for the pre-distribution of keys[J]. Automatic Control and Computer Sciences, 2020, 54(8): 860–863. doi: 10.3103/S0146411620080088 [13] WAN Zhexian. Geometry of Classical Group over Finite Fields[M]. 2nd ed. Beijing: Science Press, 2006: 108–135. [14] 沈灏. 组合设计理论[M]. 上海: 上海交通大学出版社, 2008: 1–3.SHEN Hao. Theory of Combinatorial Designs[M]. Shanghai: Shanghai Jiao Tong University Press, 2008: 1–3. [15] BLACKBURN S R, ETZION T, MARTIN K M, et al. Efficient key predistribution for grid-based wireless sensor networks[C]. 3rd International Conference on Information Theoretic Security, Calgary, Canada, 2008: 54–69. [16] BECHKIT W, CHALLAL Y, BOUABDALLAH A, et al. A highly scalable key pre-distribution scheme for wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(2): 948–959. doi: 10.1109/TWC.2012.010413.120732 [17] RUJ S, NAYAK A, and STOJMENOVIC I. Pairwise and triple key distribution in wireless sensor networks with applications[J]. IEEE Transactions on Computers, 2013, 62(11): 2224–2237. doi: 10.1109/TC.2012.138 -







 下载:
下载:








 下载:
下载:
