Design of High Precision Low Power Approximate Floating-point Multiplier Based on Partial Product Probability Analysis
-
摘要: 浮点乘法器是高动态范围(HDR)图像处理、无线通信等系统中的关键运算单元,其相比于定点乘法器动态范围更广,但复杂度更高。近似计算作为一种新兴范式,在受限的精度损失范围内,可大幅降低硬件资源和功耗开销。该文提出一种16 bit半精度近似浮点乘法器(App-Fp-Mul),针对浮点乘法器中的尾数乘法模块,根据其部分积阵列中出现1的概率,提出一种对输入顺序不敏感的近似4-2压缩器及低位或门压缩方法,在精度损失较小的条件下有效降低了浮点乘法器资源及功耗。相较于精确设计,所提近似浮点乘法器在归一化平均错误距离(NMED)为0.0014时,面积及功耗延时积方面分别降低20%及58%;相较于现有近似设计,在近似位宽相同时具有更高的精度及更小的功耗延时积。最后将该文所提近似浮点乘法器应用于高动态范围图像处理,相比现有主流方案,峰值信噪比和结构相似性分别达到83.16 dB 和 99.9989%,取得了显著的提升。Abstract: Floating-point multipliers are the key operational units in High Dynamic Range(HDR) image processing and wireless communication systems. Compared to the fixed-point multipliers, floating-point multipliers have a higher dynamic range and also higher complexity. As a newly emerging paradigm, the hardware resources and power consumption of the circuits can be greatly reduced by approximate computing within an acceptable accuracy loss. According to the probability of 1 in the partial product array, an Approximate Floating-point Multiplier(App-Fp-Mul) is proposed in this paper. An approximate 4-2 compressor and or-gate based compression method are proposed to reduce the resource and power consumption of the floating-point multiplier with small precision loss. Compared with the accurate design, the proposed approximate floating-point multiplier can reduce the area, and power delay product by 20%, and 58% respectively when the Normalized Mean Error Distance (NMED) is 0.0014. And the proposed floating-point multiplier has higher accuracy and a smaller power delay product than the existing approximate designs with the same approximate bit width. Finally, the proposed approximate floating-point multiplier is verified with high dynamic range image processing application. The result of processing can reach 83.16 dB peak signal to noise ratio and 99.9989% structure similarity, which is obviously better than the existing approximate design.
-
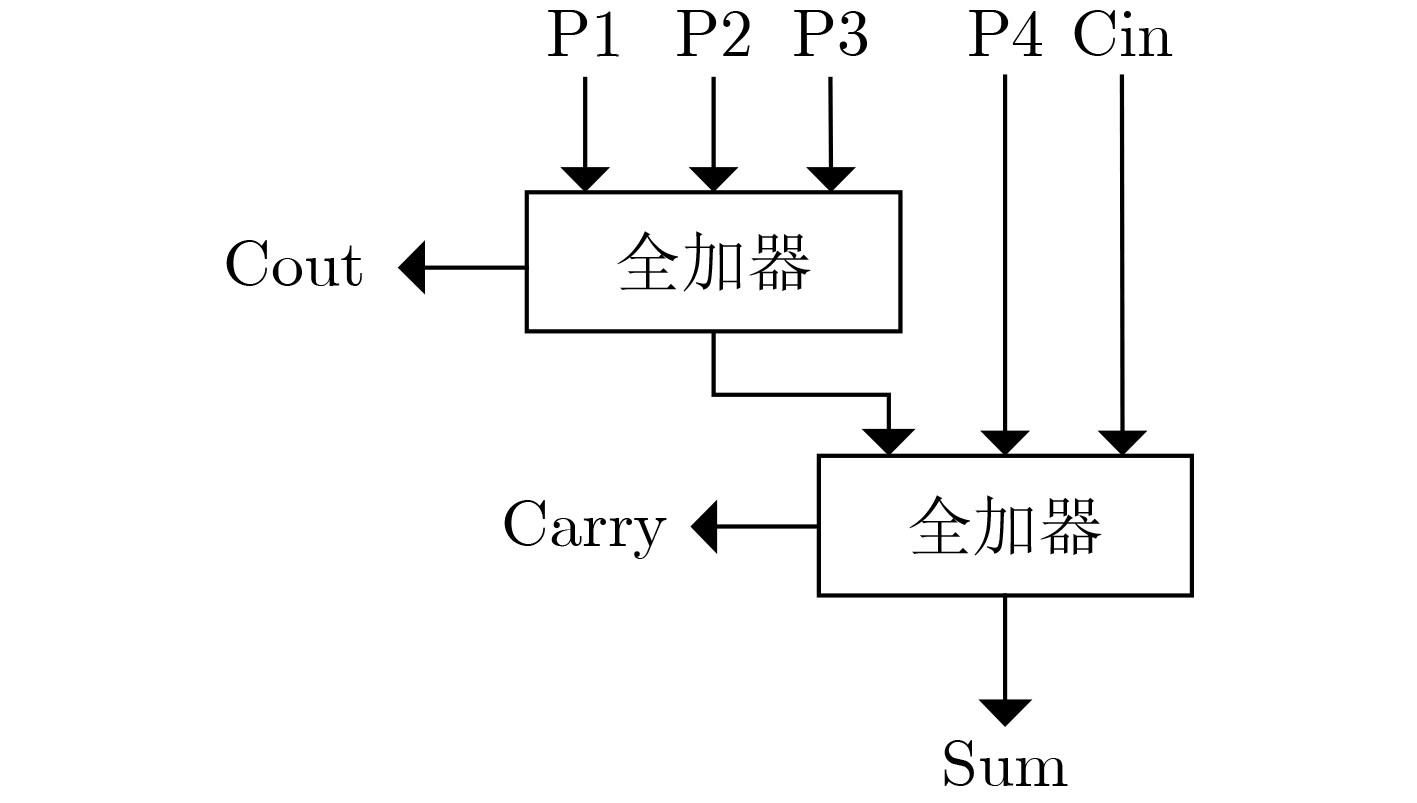
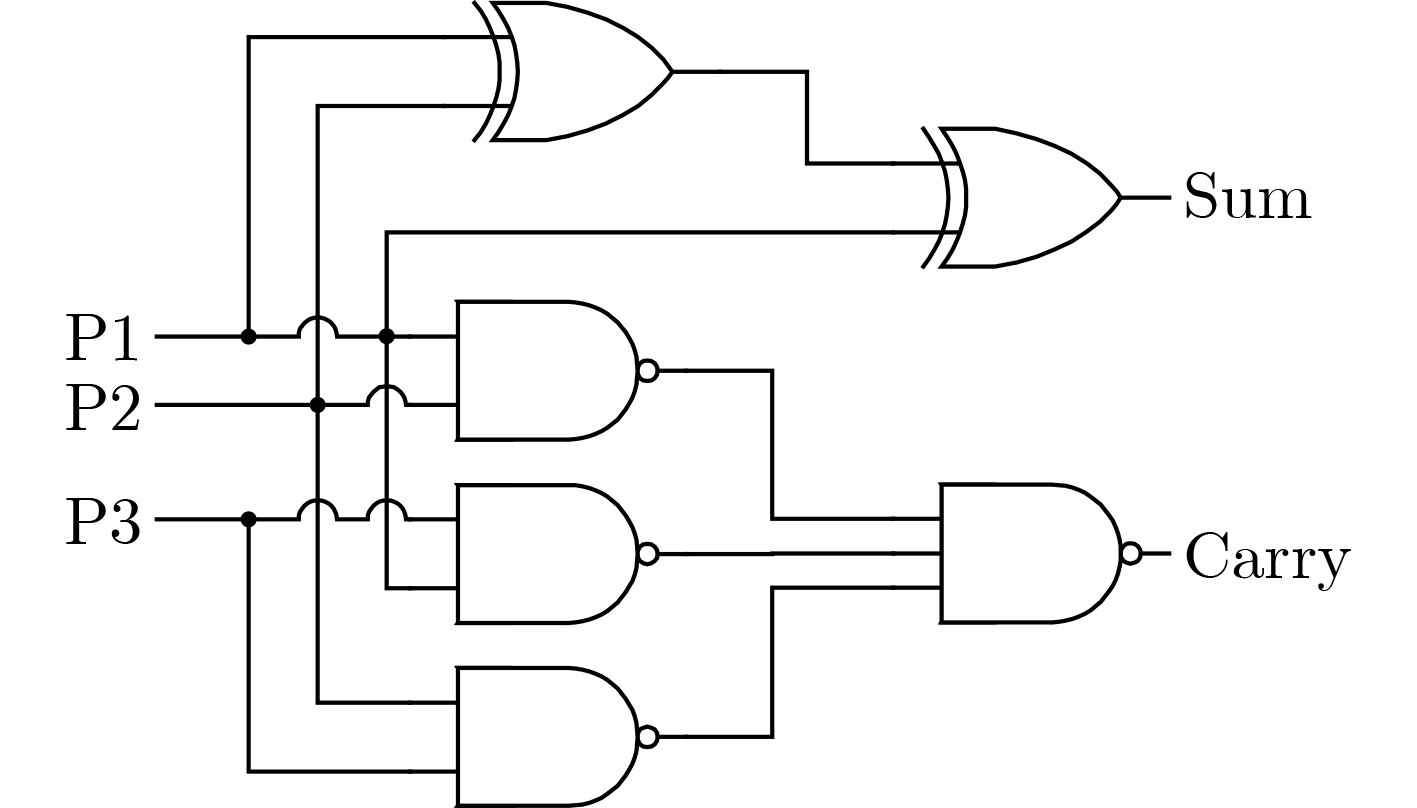
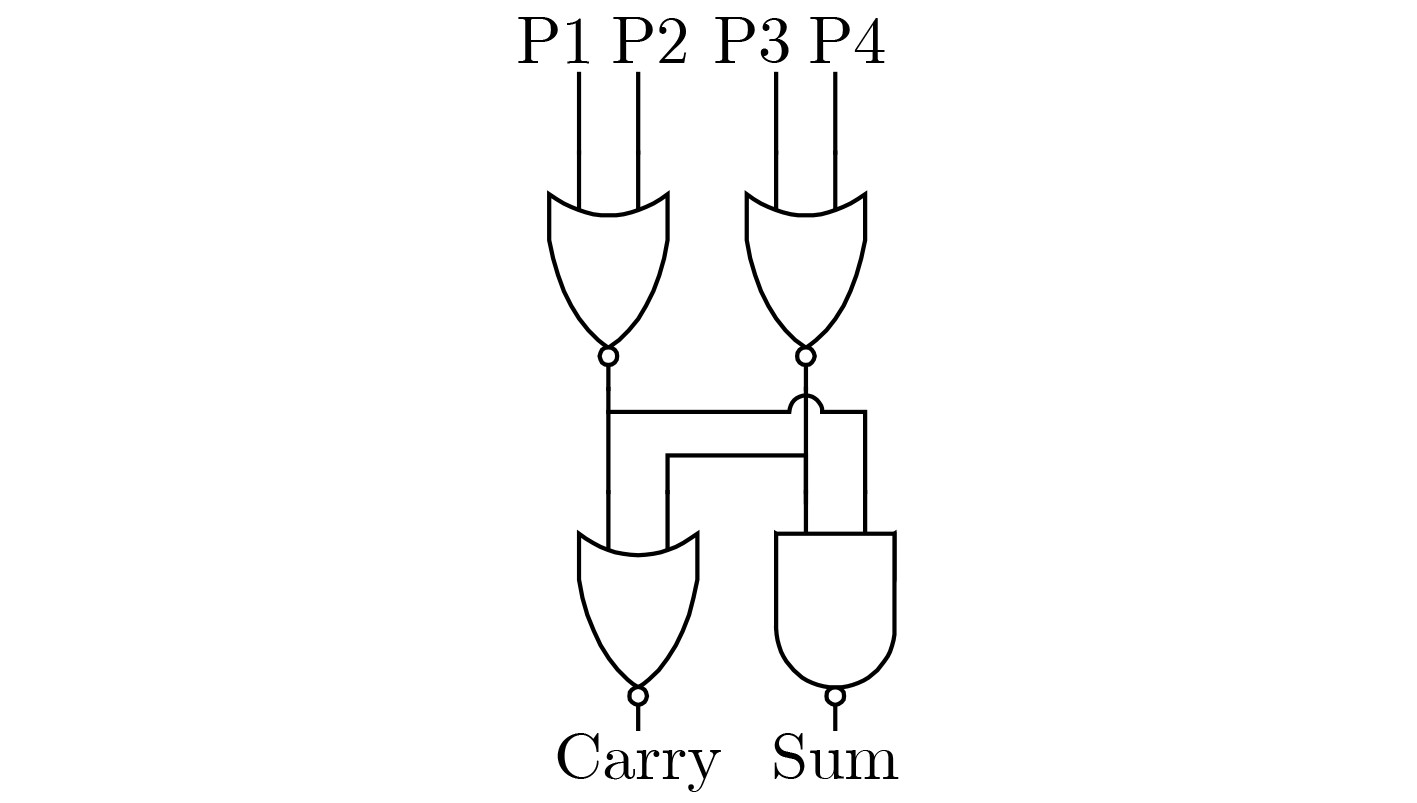
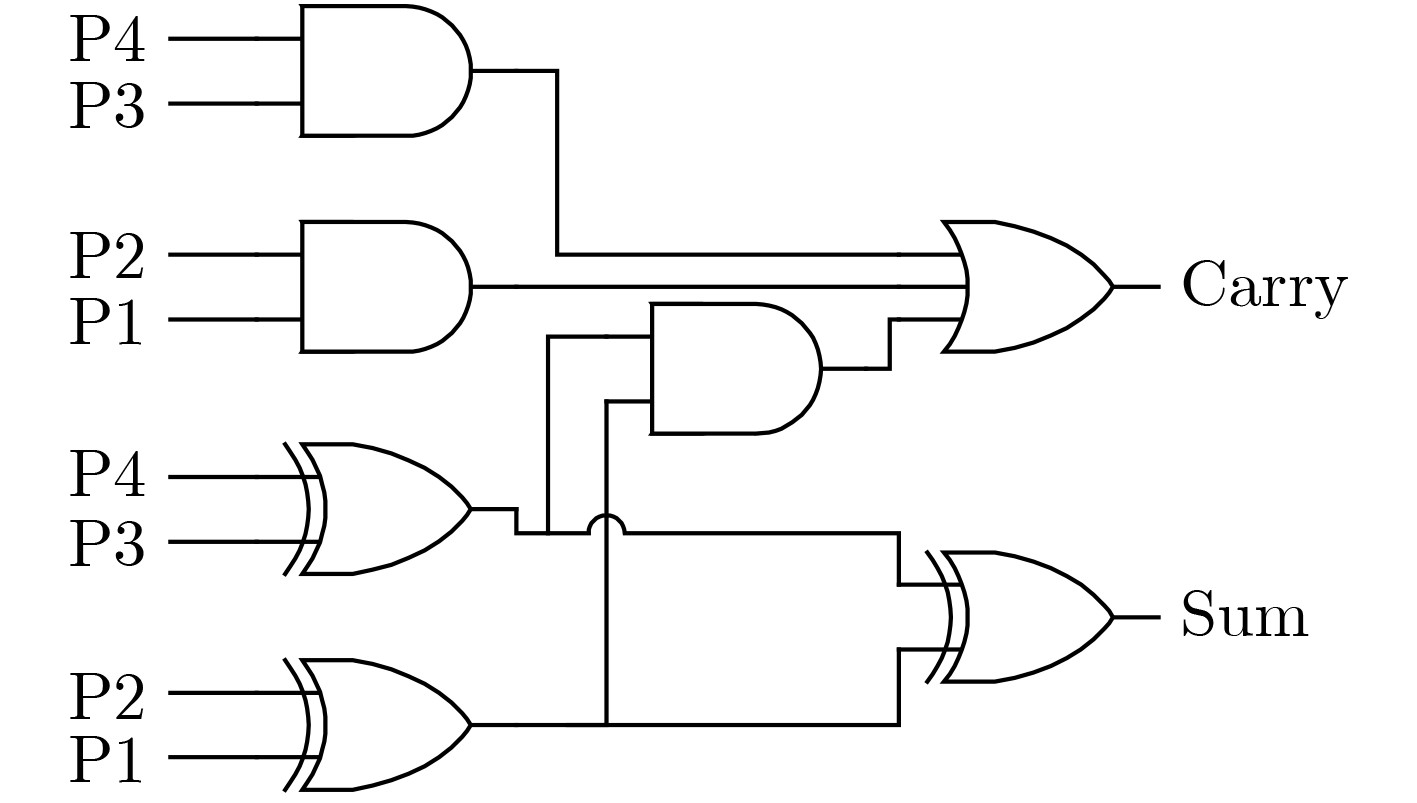
图 4 Ahma近似4-2压缩器[22]
表 1 浮点数的尾数中1的概率
权重 A[10] A[9] A[8] A[7] A[6] A[5] A[4] A[3] A[2] A[1] A[0] 高斯分布 0.97 0.42 0.46 0.48 0.49 0.49 0.50 0.50 0.50 0.50 0.50 表 2 门电路的延时[24]
AND OR XOR 归一化延时 0.7 0.7 1.0 晶体管数目 2N+2 2N+2 4N+2 表 3 近似 4-2 压缩器真值表
P1 P2 P3 P4 Sum Carry Error 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 0 1 0 0 1 0 0 0 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 0 0 0 1 0 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 1 –2 表 4 或门真值表
P1 P2 Out Error 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 –1 表 5 近似尾数乘法器精度指标
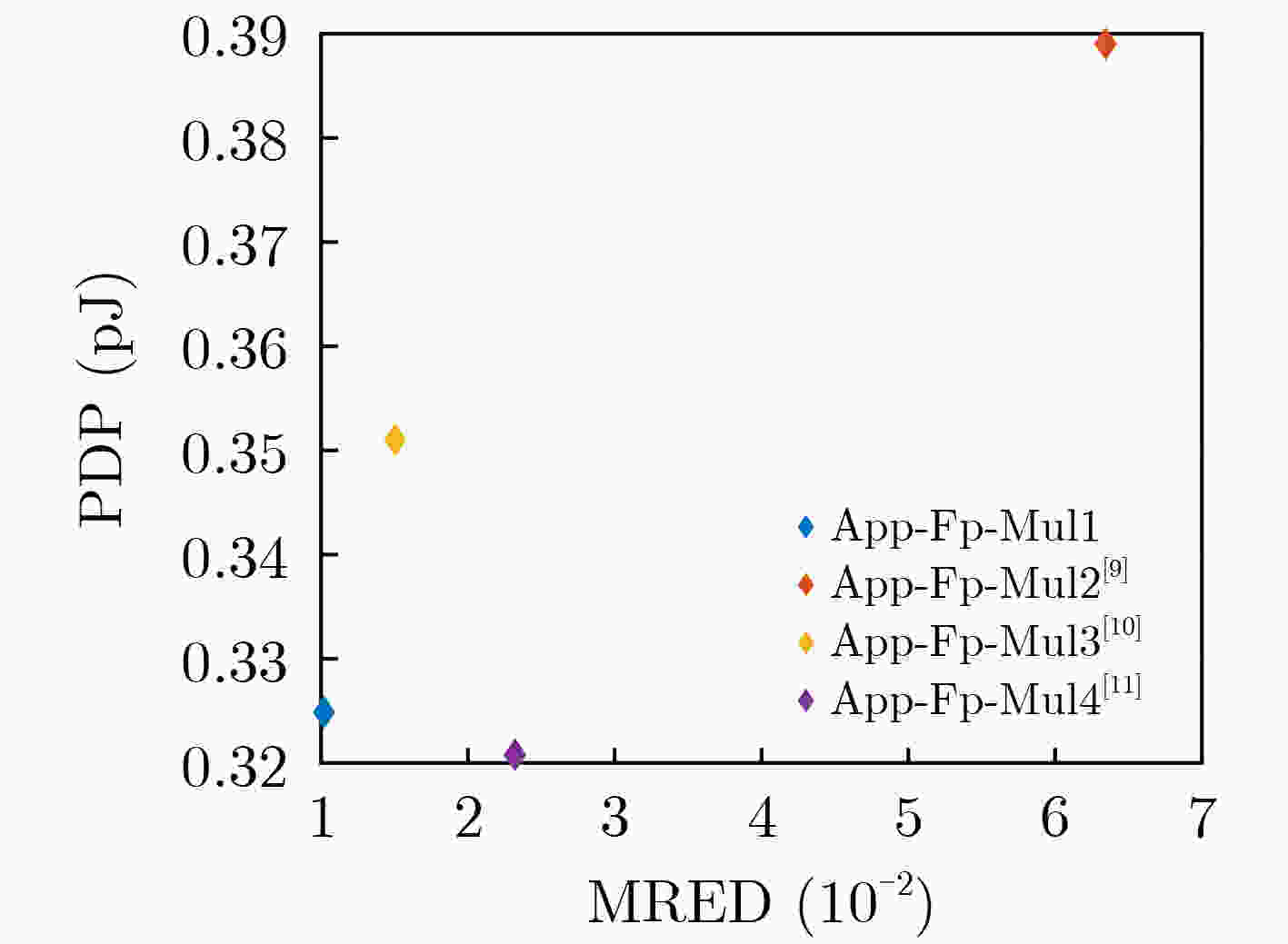
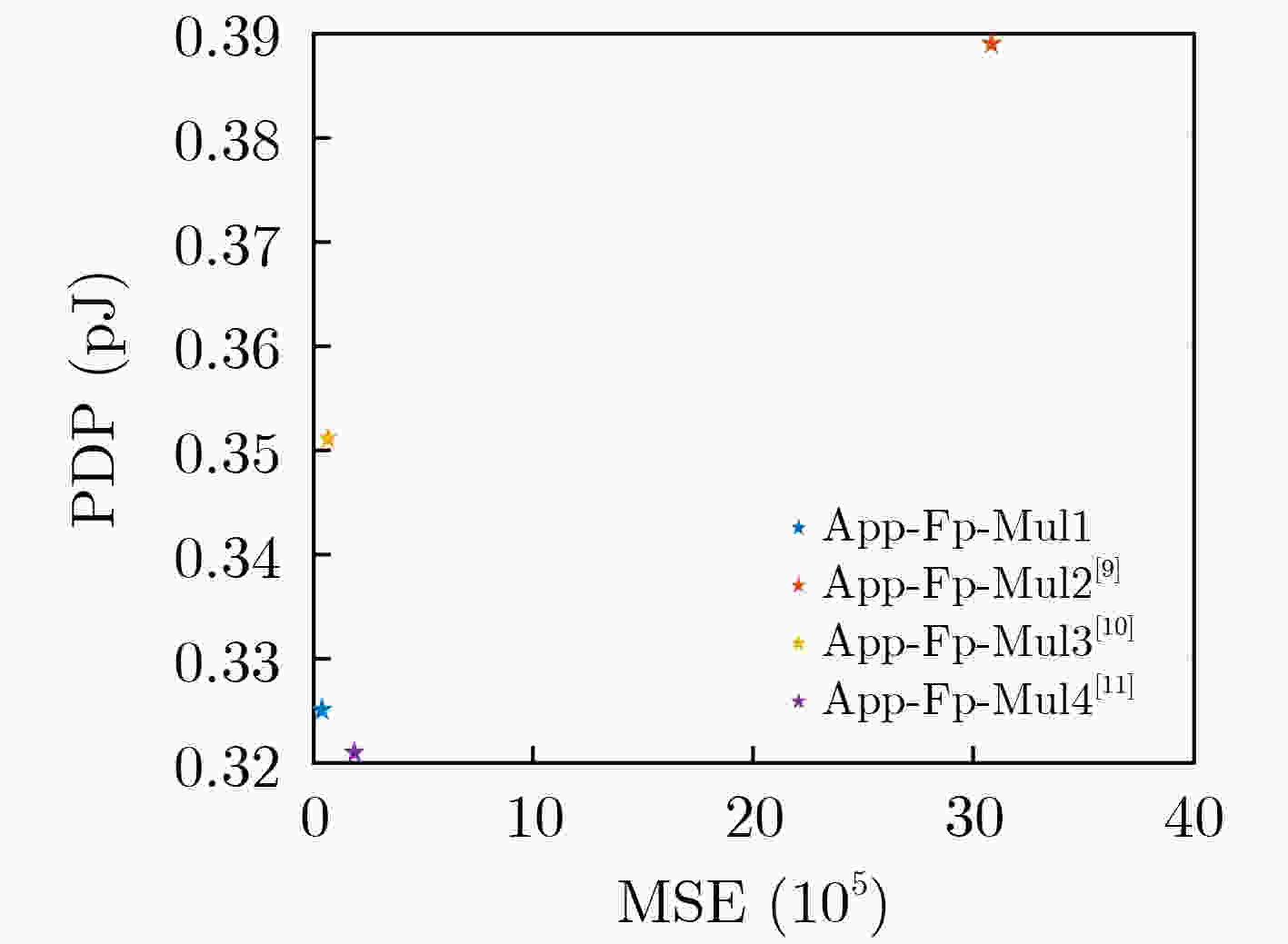
表 6 近似浮点乘法器精度指标
表 7 近似乘法器硬件指标(仿真频率500 MHz)
表 8 近似浮点乘法器硬件指标(仿真频率200 MHz)
-
[1] LIU Weiqiang, LOMBARDI F, and SHULTE M. A retrospective and prospective view of approximate computing[J]. Proceedings of the IEEE, 2020, 108(3): 394–399. doi: 10.1109/JPROC.2020.2975695 [2] WILSON L. International technology roadmap for semiconductors (ITRS)[EB/OL]. https://www.semiconductors.org/resources/2013-international-technology-roadmap-for-semiconductors-itrs/, 2013. [3] VENKATARAMANI S, CHAKRADHAR ST, ROY K, et al. Computing approximately, and efficiently[C]. 2015 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 2015: 748–751. [4] CHIPPA V K, CHAKRADHAR S T, ROY K, et al. Analysis and characterization of inherent application resilience for approximate computing[C]. The 50th Annual Design Automation Conference (DAC), Austin, USA, 2013: 113. [5] LIU Bo, CAI Hao, WANG Zhen, et al. A 22nm, 10.8 $\mu $ W/15.1$\mu $ W dual computing modes high power-performance-area efficiency domained background noise aware keyword- spotting processor[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2020, 67(12): 4733–4746. doi: 10.1109/TCSI.2020.2997913[6] LIU Bo, DING Xiaoling, CAI Hao, et al. Precision adaptive MFCC based on R2SDF-FFT and approximate computing for low-power speech keywords recognition[J]. IEEE Circuits and Systems Magazine, 2021, 21(4): 24–39. doi: 10.1109/MCAS.2021.3118175 [7] WARIS H, WANG Chenghua, LIU Weiqiang, et al. Hybrid low radix encoding-based approximate booth multipliers[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(12): 3367–3371. doi: 10.1109/TCSII.2020.2975094 [8] VENKATACHALAM S, ADAMS E, LEE H J, et al. Design and analysis of area and power efficient approximate booth multipliers[J]. IEEE Transactions on Computers, 2019, 68(11): 1697–1703. doi: 10.1109/TC.2019.2926275 [9] LIU Weiqiang, QIAN Liangyu, WANG Chenghua, et al. Design of approximate radix-4 booth multipliers for error-tolerant computing[J]. IEEE Transactions on Computers, 2017, 66(8): 1435–1441. doi: 10.1109/TC.2017.2672976 [10] YI Xilin, PEI Haoran, ZHANG Ziji, et al. Design of an energy-efficient approximate compressor for error-resilient multiplications[C]. 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 2019: 1–5. [11] FANG Bao, LIANG Huaguo, XU Dawen, et al. Approximate multipliers based on a novel unbiased approximate 4–2 compressor[J]. Integration, 2021, 81: 17–24. doi: 10.1016/j.vlsi.2021.05.003 [12] HA M and LEE S. Multipliers with approximate 4–2 compressors and error recovery modules[J]. IEEE Embedded Systems Letters, 2018, 10(1): 6–9. doi: 10.1109/LES.2017.2746084 [13] AKBARI O, KAMAL M, AFZALI-KUSHA A, et al. Dual-quality 4: 2 compressors for utilizing in dynamic accuracy configurable multipliers[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2017, 25(4): 1352–1361. doi: 10.1109/TVLSI.2016.2643003 [14] SABETZADEH F, MOAIYERI M H, and AHMADINEJAD M. A majority-based imprecise multiplier for ultra-efficient approximate image multiplication[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2019, 66(11): 4200–4208. doi: 10.1109/TCSI.2019.2918241 [15] PEI Haoran, YI Xilin, ZHOU Hang, et al. Design of ultra-low power consumption approximate 4–2 compressors based on the compensation characteristic[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2021, 68(1): 461–465. doi: 10.1109/TCSII.2020.3004929 [16] NIU Zijing, JIANG Honglan, ANSARI M S, et al. A logarithmic floating-point multiplier for the efficient training of neural networks[C]. The 2021 on Great Lakes Symposium on VLSI, New York, USA, 2021: 65–70. [17] JHA C K, WALIA S, KANOJIA G, et al. FPCAM: Floating point configurable approximate multiplier for error resilient applications[C]. 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Korea, 2021: 1–5. [18] YIN Peipei, WANG Chenghua, LIU Weiqiang, et al. Design and performance evaluation of approximate floating-point multipliers[C]. 2016 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Pittsburgh, USA, 2016: 296–301. [19] IEEE. IEEE Std 754–2008 IEEE standard for floating-point arithmetic[S]. IEEE, 2008. [20] TONG J Y F, NAGLE D, and RUTENBAR R A. Reducing power by optimizing the necessary precision/range of floating-point arithmetic[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2000, 8(3): 273–286. doi: 10.1109/92.845894 [21] HSIAO S F, JIANG M R, YEH J S. Design of high-speed low-power 3–2 counter and 4–2 compressor for fast multipliers[J]. Electronics Letters, 1998, 34(4): 341–343. doi: 10.1049/el:19980306 [22] AHMADINEJAD M, MOAIYERI M H, and SABETZADEH F. Energy and area efficient imprecise compressors for approximate multiplication at nanoscale[J]. AEU- International Journal of Electronics and Communications, 2019, 110: 152859. doi: 10.1016/j.aeue.2019.152859 [23] STROLLO A G M, NAPOLI E, DE CARO D, et al. Comparison and extension of approximate 4–2 compressors for low-power approximate multipliers[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2020, 67(9): 3021–3034. doi: 10.1109/TCSI.2020.2988353 [24] 朱玉莹. 优化的近似Booth乘法器设计和评估及概率错误模型分析[D]. [硕士论文], 南京航空航天大学, 2020: 13–15.ZHU Yuying. Design and evaluation of improved approximate Booth multipliers and probabilistic error model analysis[D]. [Master dissertation], Nanjing University of Aeronautics and Astronautics, 2020: 13–15. -





 下载:
下载:




 下载:
下载:
