Outlier-robust Tri-percentile Parameter Estimation Method of Compound-Gaussian Clutter with Inverse Gaussian Textures
-
摘要: 逆高斯纹理的复合高斯分布(IG-CG分布)是描述高分辨率海杂波常用的模型,其参数估计在高分辨海用雷达自适应目标检测中起着关键作用。由于参数估计中数据不可避免地存在来自海面目标、岛礁的异常样本,对异常样本稳健的双分位点估计是近年来提出的有效方法之一。该文提出一种对异常点稳健的IG-CG分布三分位点参数估计(Tri-per)方法,其是对双分位点估计的改进。改进来自两个方面,通过双分位点位置优化提高逆形状参数的估计精度;通过第3个分位点的引入和位置优化提高尺度参数的估计精度。最后,用仿真和实测数据检验了提出估计方法的有效性和稳健性。
-
关键词:
- 逆高斯-复合高斯分布 /
- 稳健参数估计 /
- 海杂波幅度模型 /
- 三分位点估计
Abstract: Compound-Gaussian distributions with Inverse Gaussian textures (IG-CG distributions) are commonly-used model to characterize high-resolution sea clutter and its parameter estimation plays an important role in adaptive target detection in high-resolution maritime radars. In parameter estimation, sea clutter data unavoidably contain a few of outliers from radar returns of sea-surface objects and reefs and in this case outlier-robust bi-percentile estimators are one of effective methods. This paper proposes an outlier-robust Tripercentile (Tri-per) estimation method, which is an improved version of the bi-percentile estimators. The improvement is made in two aspects. The positions of two sample percentiles are optimized to improve the estimation precision of the inverse shape parameter and the third sample percentile is introduced and its position is optimized to improve the estimation precision of the scale parameter. At last, simulated and measured data are used to verify the effectiveness and robustness of the proposed tri-percentile estimators. -
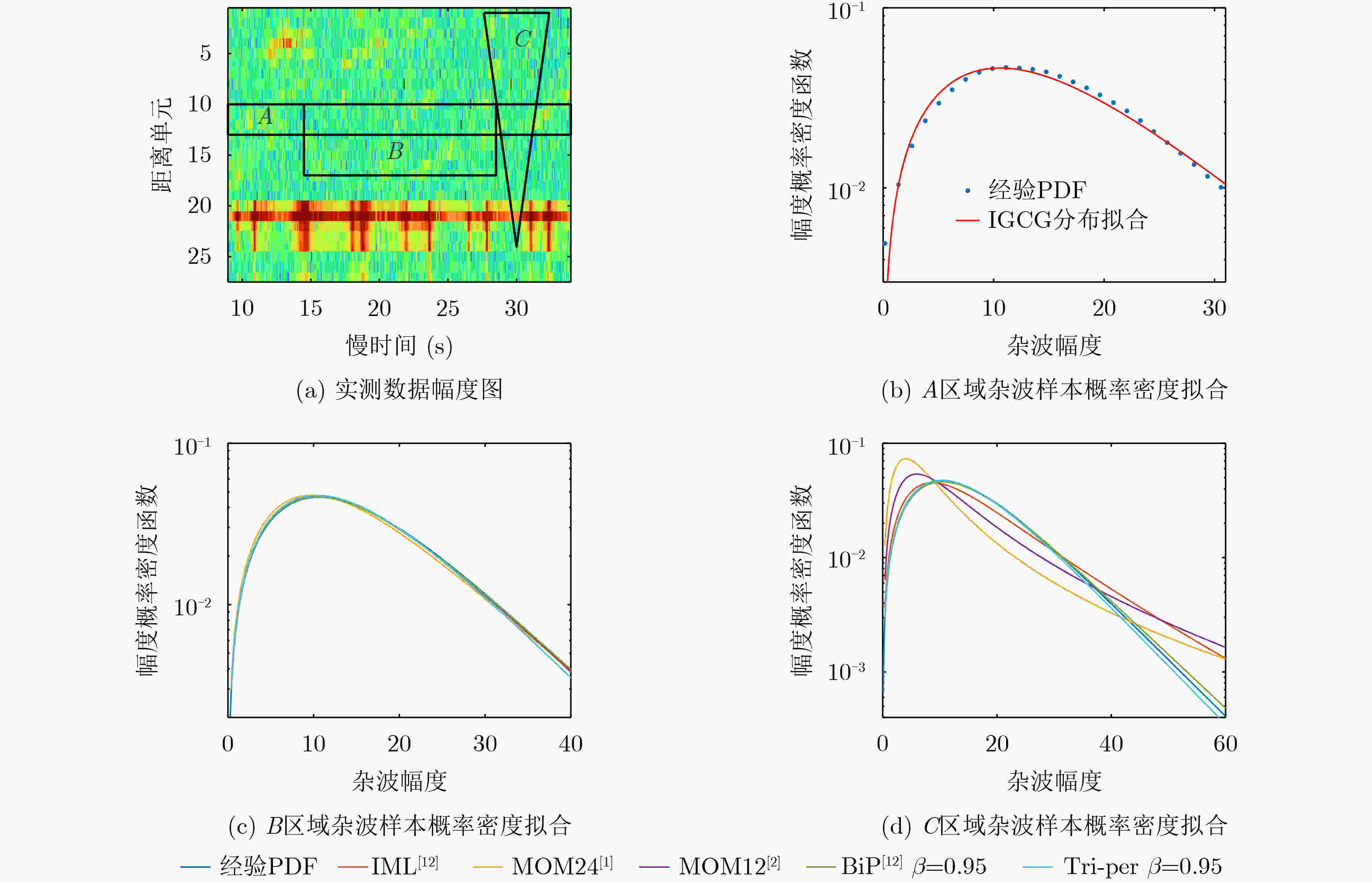
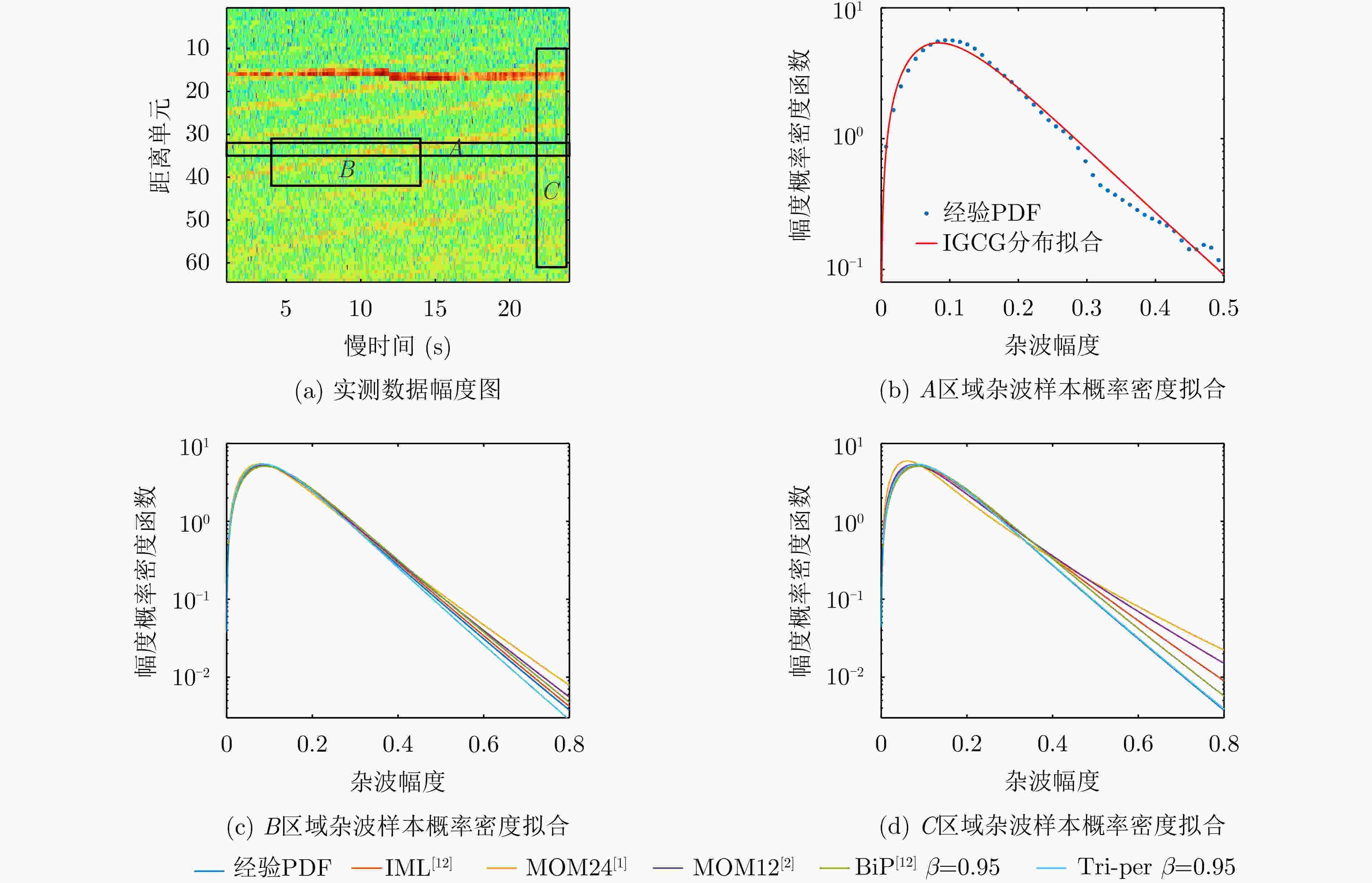
表 1 IPIX实测数据(19980223_184853_ANTSTEP)的估计结果
估计方法 区域 逆形参 尺参(×100) K-S距离 IML[12] 区域A 0.4726 3.8922 0.0205 MOM24[1] 纯杂波区域B 0.6406 3.8575 0.0398 MOM12[2] 0.4764 3.8575 0.0238 IML[12] 0.5008 3.8199 0.0230 BiP[12]$\beta = 0.95$ 0.5077 3.9084 0.0236 Tri-per$\beta = 0.95$ 0.4336 3.6615 0.0269 MOM24[1] 含2%异常点的区域C 11.1026 7.2643 0.2708 MOM12[2] 5.0000 7.2643 0.1388 IML[12] 1.5436 5.4478 0.0629 BiP[12]$\beta = 0.95$ 0.5297 4.0148 0.0270 Tri-per$\beta = 0.95$ 0.4626 3.7040 0.0269 表 2 南非CSIR实测数据(TFA10_001.01)的估计结果
估计方法 区域 逆形参 尺参 K-S距离 IML[12] 区域A 0.7576 0.0310 0.0259 MOM24[1] 纯杂波区域B 1.0879 0.0331 0.0504 MOM12[2] 0.8407 0.0331 0.0296 IML[12] 0.7358 0.0324 0.0278 BiP[12]$\beta = 0.95$ 0.7034 0.0341 0.0443 Tri-per$\beta = 0.95$ 0.6910 0.0300 0.0343 MOM24[1] 含2%异常点的区域C 2.3473 0.0377 0.1058 MOM12[2] 1.4151 0.0377 0.0454 IML[12] 1.0060 0.0357 0.0346 BiP[12]$\beta = 0.95$ 0.7624 0.0348 0.0297 Tri-per$\beta = 0.95$ 0.7571 0.0313 0.0287 -
[1] OLLILA E, TYLER D E, KOIVUNEN V, et al. Compound-Gaussian clutter modeling with an inverse Gaussian texture distribution[J]. IEEE Signal Processing Letters, 2012, 19(12): 876–879. doi: 10.1109/LSP.2012.2221698 [2] YU Han, SHUI Penglang, and HUANG Yuting. Low-order moment-based estimation of shape parameter of CGIG clutter model[J]. Electronics Letters, 2016, 52(18): 1561–1563. doi: 10.1049/el.2016.2248 [3] WANG Zhihang, HE Zishu, HE Qin, et al. Adaptive CFAR detectors for mismatched signal in compound Gaussian sea clutter with inverse Gaussian texture[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 3502705. doi: 10.1109/LGRS.2020.3047390 [4] GRIFFITHS H. Sea clutter: Scattering, the K distribution and radar performance (Ward, K. D., et al.; 2006) [book review][J]. IEEE Aerospace and Electronic Systems Magazine, 2007, 22(1): 28. doi: 10.1109/MAES.2007.327513 [5] 张坤, 水鹏朗, 王光辉. 相参雷达K分布海杂波背景下非相干积累恒虚警检测方法[J]. 电子与信息学报, 2020, 42(7): 1627–1635. doi: 10.11999/JEIT190441ZHANG Kun, SHUI Penglang, and WANG Guanghui. Non-coherent integration constant false alarm rate detectors against K-distributed sea clutter for coherent radar systems[J]. Journal of Electronics &Information Technology, 2020, 42(7): 1627–1635. doi: 10.11999/JEIT190441 [6] BALLERI A, NEHORAI A, and WANG Jian. Maximum likelihood estimation for compound-gaussian clutter with inverse gamma texture[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 775–779. doi: 10.1109/TAES.2007.4285370 [7] CHALABI I and MEZACHE A. Estimators of compound Gaussian clutter with log-normal texture[J]. Remote Sensing Letters, 2019, 10(7): 709–716. doi: 10.1080/2150704X.2019.1601275 [8] XUE Jian, XU Shuwen, and SHUI Penglang. Near-optimum coherent CFAR detection of radar targets in compound-Gaussian clutter with inverse Gaussian texture[J]. Signal Processing, 2020, 166: 107236. doi: 10.1016/j.sigpro.2019.07.029 [9] XU Shuwen, WANG Zhexiang, BAI Xiaohui, et al. Optimum and near-optimum coherent CFAR detection of radar targets in compound-Gaussian clutter with generalized inverse Gaussian texture[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(3): 1692–1706. doi: 10.1109/TAES.2021.3120045 [10] MEZACHE A, SOLTANI F, SAHED M, et al. Model for non-rayleigh clutter amplitudes using compound inverse Gaussian distribution: An experimental analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 142–153. doi: 10.1109/TAES.2014.130332 [11] HUANG Penghui, ZOU Zihao, XIA Xianggen, et al. A statistical model based on modified generalized-K distribution for sea clutter[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 8015805. doi: 10.1109/LGRS.2021.3093975 [12] SHUI Penglang, SHI Lixiang, YU Han, et al. Iterative maximum likelihood and outlier-robust bipercentile estimation of parameters of compound-Gaussian clutter with inverse Gaussian texture[J]. IEEE Signal Processing Letters, 2016, 23(11): 1572–1576. doi: 10.1109/LSP.2016.2605129 [13] YU Han, SHUI Penglang, and LU Kai. Outlier-robust tri-percentile parameter estimation of K-distributions[J]. Signal Processing, 2021, 181: 107906. doi: 10.1016/j.sigpro.2020.107906 [14] MIAO Yu, CHEN Yingxia, and XU Shoufang. Asymptotic properties of the deviation between order statistics and p-quantile[J]. Communications in Statistics-Theory and Methods, 2010, 40(1): 8–14. doi: 10.1080/03610920903350523 [15] http://soma.crl.mcmast.ca/ipix.2020. [16] http://www.csir.co.ca/small_boat_detection.2020. -





 下载:
下载:


 下载:
下载:
