Reverse Order and Greedy Integrated Scheduling Algorithm Considering Dynamic Time Urgency Degree of the Process Sequences
-
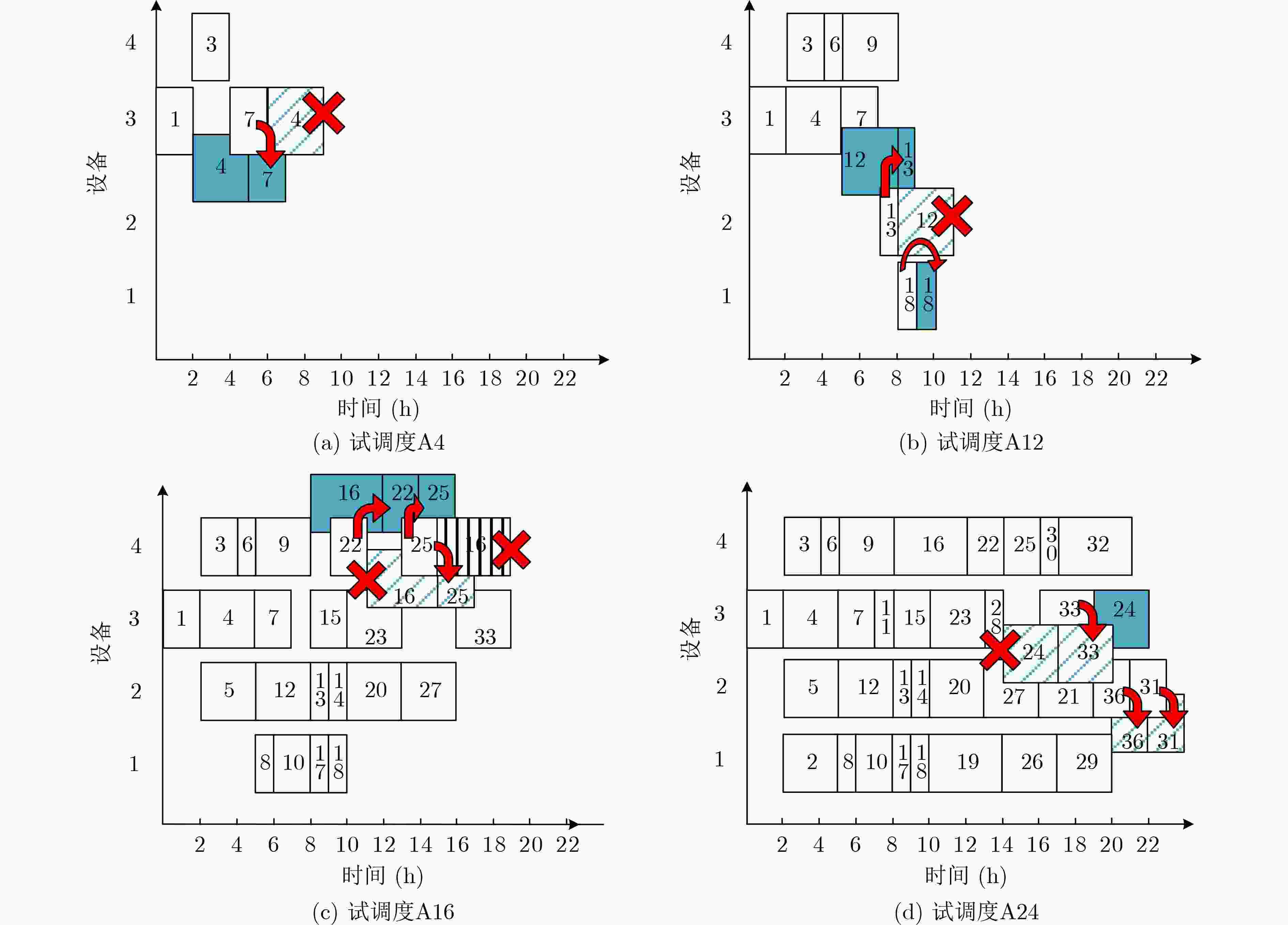
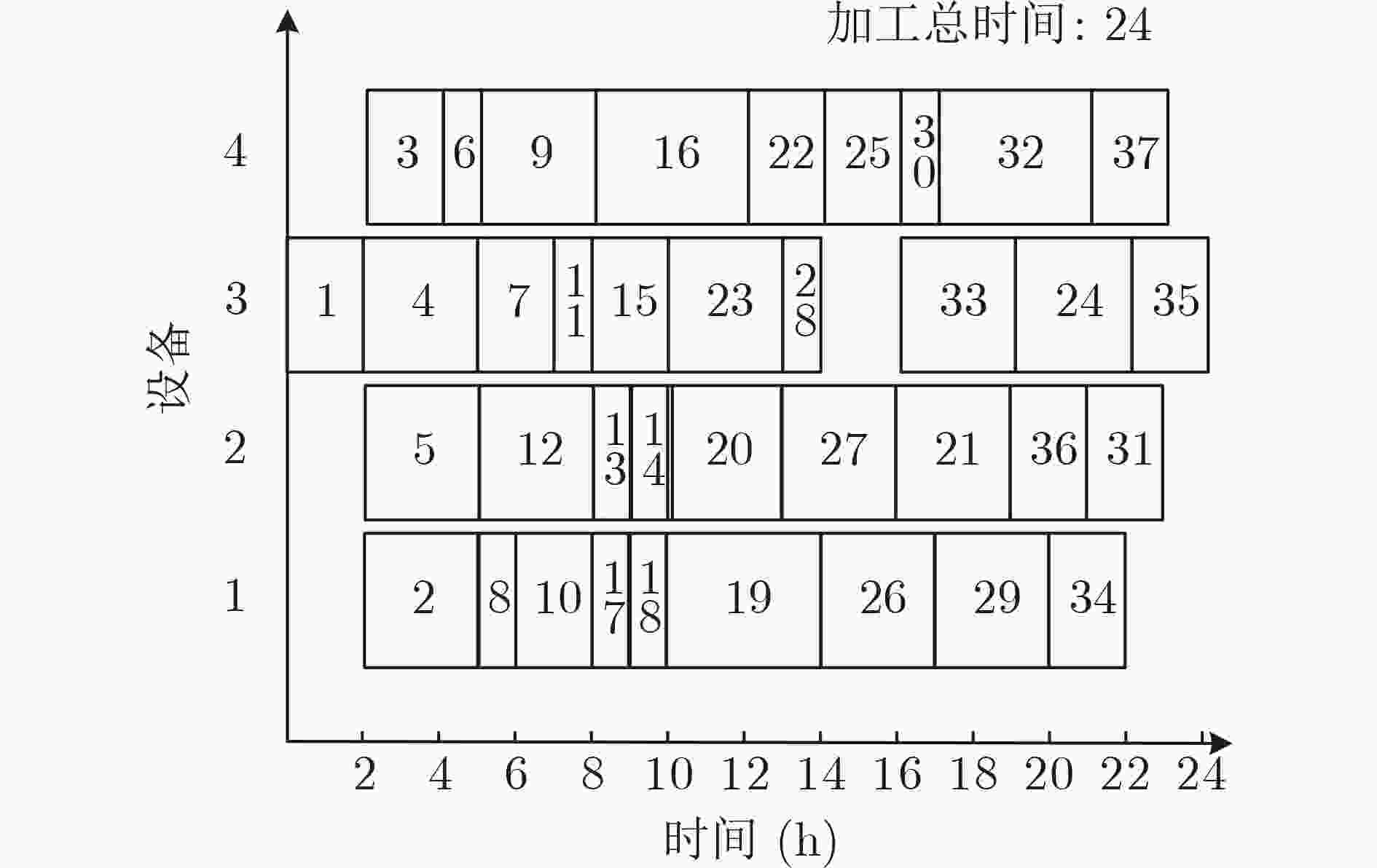
摘要: 针对树状结构复杂单产品加工和装配的一般综合调度问题,该文提出考虑工序序列动态时间紧迫度(TUD)的逆序贪婪综合调度算法。提出工序排序策略,定义工序序列的时间紧迫度,将工序树逆置,采用叶对齐的方式,按照由叶到根的顺序,逐层根据叶结点所属工序序列动态时间紧迫度值由大到小的顺序确定其调度顺序,将各层排序后的叶结点依次入队列保存,最后将队列中元素逆置。提出逆序贪婪调度策略,每次以一道工序为单位,安排它在所需设备上的准调度时间点进行试调度,得到该工序的准调度方案集,选择准调度方案结束时间最小的方案,若不唯一,选择使该工序尽早加工的方案。实例表明所提算法优化了一般综合调度的结果且效率较高。Abstract: For the general integrated scheduling problem of tree structured complex single product machining and assembling, a reverse order and greedy integrated scheduling algorithm is proposed by considering dynamic TUD (Time Urgency Degree) of the process sequences. The strategy of process sorting is put forward, and the TUD of process sequence is defined. The process tree is reversed using leaf alignment, according to the order from leaf to root, the scheduling order of leaf nodes in the same layer is determined layer by layer from large to small according to the dynamic TUD values of the process sequences to which the leaf nodes belong. The sorted leaf nodes are put into the queue in turn. Finally, the elements in the queue are reversed. A reverse order and greedy scheduling strategy is proposed. Each time, a single process is taken as a unit to conduct trial scheduling at the quasi-scheduling time point in the required equipment. Quasi-scheduling scheme set of the process is obtained, and the quasi-scheduling scheme with the minimum end time is selected, and if it is not unique, the scheme is selected to machine the process as early as possible. A case shows that the proposed algorithm optimizes the general integrated scheduling results and has high efficiency.
-
Key words:
- Integrated scheduling /
- Machining and assembling /
- Time Urgency Degree (TUD) /
- Reverse order /
- Greedy
-
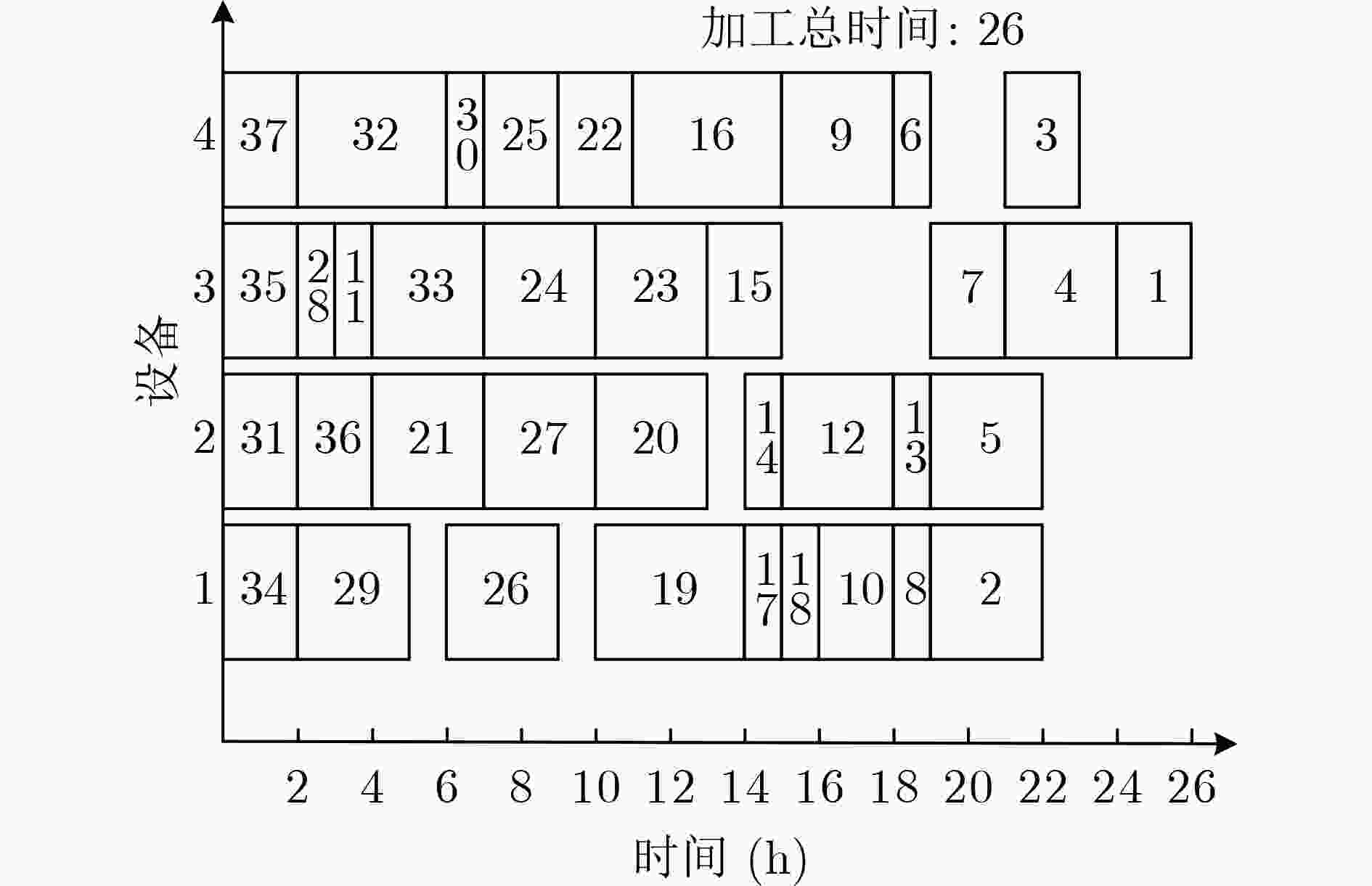
图 2 使用文献[11]算法调度产品A所得调度甘特图
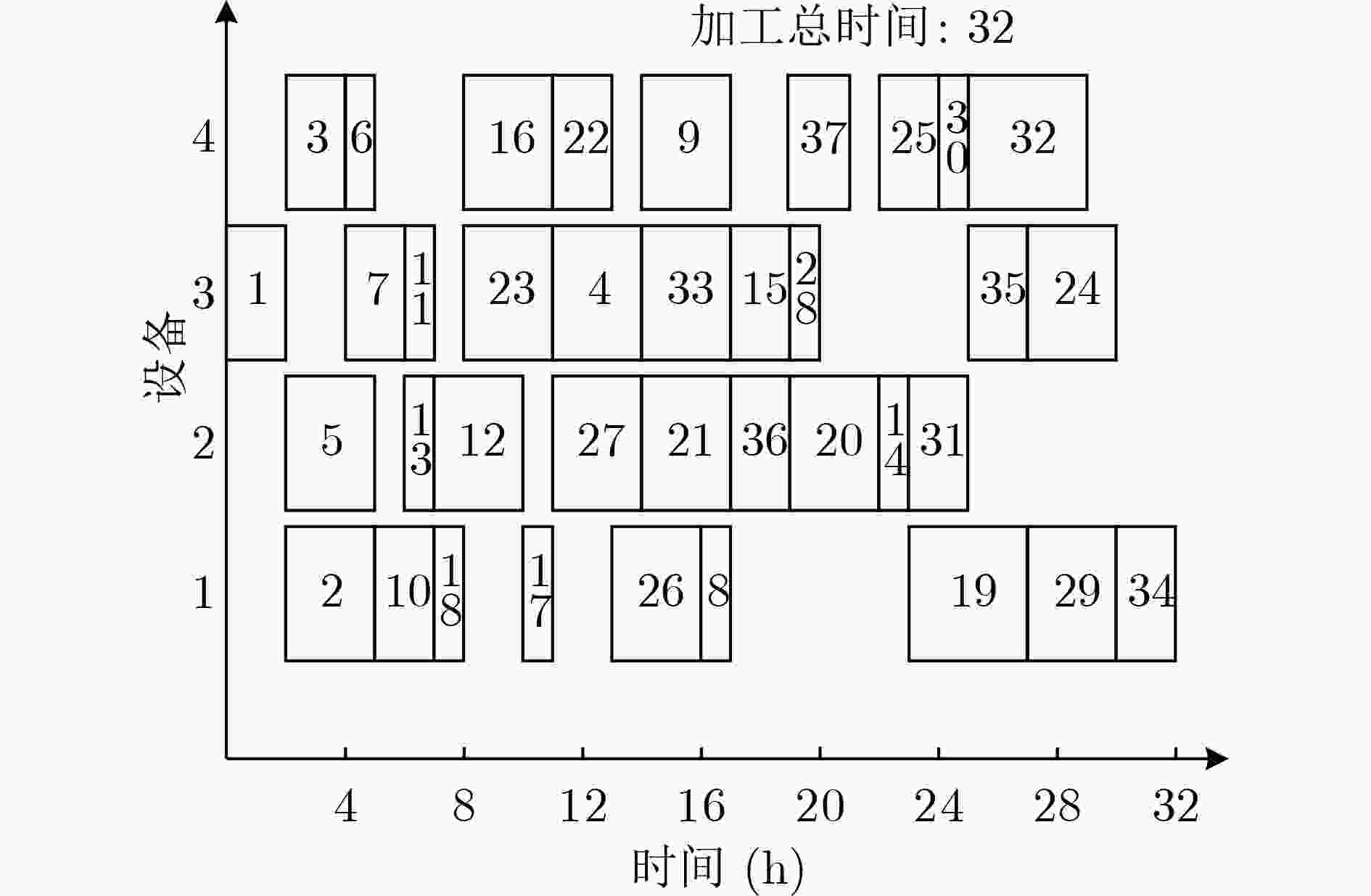
图 3 使用文献[13]算法调度产品A所得调度甘特图
-
[1] WANG Zhen, ZHANG Xiaohuan, CAO Yuxiao, et al. An integrated scheduling algorithm for multi-device-processes with the strategy of exchanging adjacent parallel processes of the same device[J]. EURASIP Journal on Wireless Communications and Networking, 2021, 2021(1): 104. doi: 10.1186/s13638-021-01989-1 [2] 苑迎春, 李小平, 王茜, 等. 基于逆向分层的网格工作流调度算法[J]. 计算机学报, 2008, 31(2): 282–290. doi: 10.3321/j.issn:0254-4164.2008.02.012YUAN Yingchun, LI Xiaoping, WANG Qian, et al. Bottom level based heuristic for workflow scheduling in grids[J]. Chinese Journal of Computers, 2008, 31(2): 282–290. doi: 10.3321/j.issn:0254-4164.2008.02.012 [3] 苑迎春, 李小平, 王茜. 基于串归约的网格工作流费用优化方法[J]. 计算机研究与发展, 2008, 45(2): 246–253.YUAN Yingchun, LI Xiaoping, and WANG Qian. Cost optimization heuristics for grid workflows scheduling based on serial reduction[J]. Journal of Computer Research and Development, 2008, 45(2): 246–253. [4] 苑迎春, 李小平, 王茜, 等. 成本约束的网格工作流时间优化方法[J]. 计算机研究与发展, 2009, 46(2): 194–201.YUAN Yingchun, LI Xiaoping, WANG Qian, et al. Time optimization heuristics for scheduling budget-constrained grid workflows[J]. Journal of Computer Research and Development, 2009, 46(2): 194–201. [5] LI Xiaoping, QIAN Lihua, and RUIZ R. Cloud workflow scheduling with deadlines and time slot availability[J]. IEEE Transactions on Services Computing, 2018, 11(2): 329–340. doi: 10.1109/TSC.2016.2518187 [6] LI Xiaoping, YU Wei, RUIZ R, et al. Energy-aware cloud workflow applications scheduling with geo-distributed data[J]. IEEE Transactions on Services Computing, 2022, 15(2): 891–903. doi: 10.1109/TSC.2020.2965106 [7] LI Xiaoping, CHEN Fuchao, RUIZ R, et al. MapReduce task scheduling in heterogeneous geo-distributed data centers[J]. IEEE Transactions on Services Computing, To be published. [8] 李克强. 政府工作报告-2021年3月5日在第十三届全国人民代表大会第四次会议上[EB/OL]. http://www.gov.cn/gongbao/content/2021/content_5593438.htm?ivk_sa=1024320u, 2021.LI Keqiang. Government work report - at the fourth session of the 13th National People's Congress on March 5, 2021[EB/OL]. http://www.gov.cn/gongbao/content/2021/content_5593438.htm?ivk_sa=1024320u, 2021. [9] GAO Yilong, XIE Zhiqiang, YANG Dan, et al. Flexible integrated scheduling algorithm based on remaining work probability selection coding[J]. Expert Systems, 2021, 38(4): e12683. doi: 10.1111/exsy.12683 [10] 谢志强, 辛宇, 杨静. 可回退抢占的设备驱动综合调度算法[J]. 自动化学报, 2011, 37(11): 1332–1343. doi: 10.3724/SP.J.1004.2011.01332XIE Zhiqiang, XIN Yu, and YANG Jing. Machine-driven integrated scheduling algorithm with rollback-preemptive[J]. Acta Automatica Sinica, 2011, 37(11): 1332–1343. doi: 10.3724/SP.J.1004.2011.01332 [11] 谢志强, 杨静, 周勇, 等. 基于工序集的动态关键路径多产品制造调度算法[J]. 计算机学报, 2011, 34(2): 406–412. doi: 10.3724/SP.J.1016.2011.00406XIE Zhiqiang, YANG Jing, ZHOU Yong, et al. Dynamic critical paths multi-product manufacturing scheduling algorithm based on operation set[J]. Chinese Journal of Computers, 2011, 34(2): 406–412. doi: 10.3724/SP.J.1016.2011.00406 [12] 张雍达, 宋嘉. 工业4.0时代的智能制造[J]. 中国工业和信息化, 2021(9): 32–34. doi: 10.19609/j.cnki.cn10-1299/f.2021.09.002ZHANG Yongda and SONG Jia. Intelligent manufacturing in the industrial 4.0 era[J]. China Industry &Information Technology, 2021(9): 32–34. doi: 10.19609/j.cnki.cn10-1299/f.2021.09.002 [13] 谢志强, 张晓欢, 高一龙, 等. 考虑串行工序紧密度的择时综合调度算法[J]. 机械工程学报, 2018, 54(6): 191–202. doi: 10.3901/JME.2018.06.191XIE Zhiqiang, ZHANG Xiaohuan, GAO Yilong, et al. Time-selective integrated scheduling algorithm considering the compactness of serial processes[J]. Journal of Mechanical Engineering, 2018, 54(6): 191–202. doi: 10.3901/JME.2018.06.191 [14] 谢志强, 张晓欢, 辛宇, 等. 考虑后续工序的择时综合调度算法[J]. 自动化学报, 2018, 44(2): 344–362. doi: 10.16383/j.aas.2018.c160562XIE Zhiqiang, ZHANG Xiaohuan, XIN Yu, et al. Time-selective integrated scheduling algorithm considering posterior processes[J]. Acta Automatica Sinica, 2018, 44(2): 344–362. doi: 10.16383/j.aas.2018.c160562 [15] WANG Zhen, ZHANG Xiaohuan, and PENG Gang. An improved integrated scheduling algorithm with process sequence time-selective strategy[J]. Complexity, 2021, 2021: 5570575. doi: 10.1155/2021/5570575 -





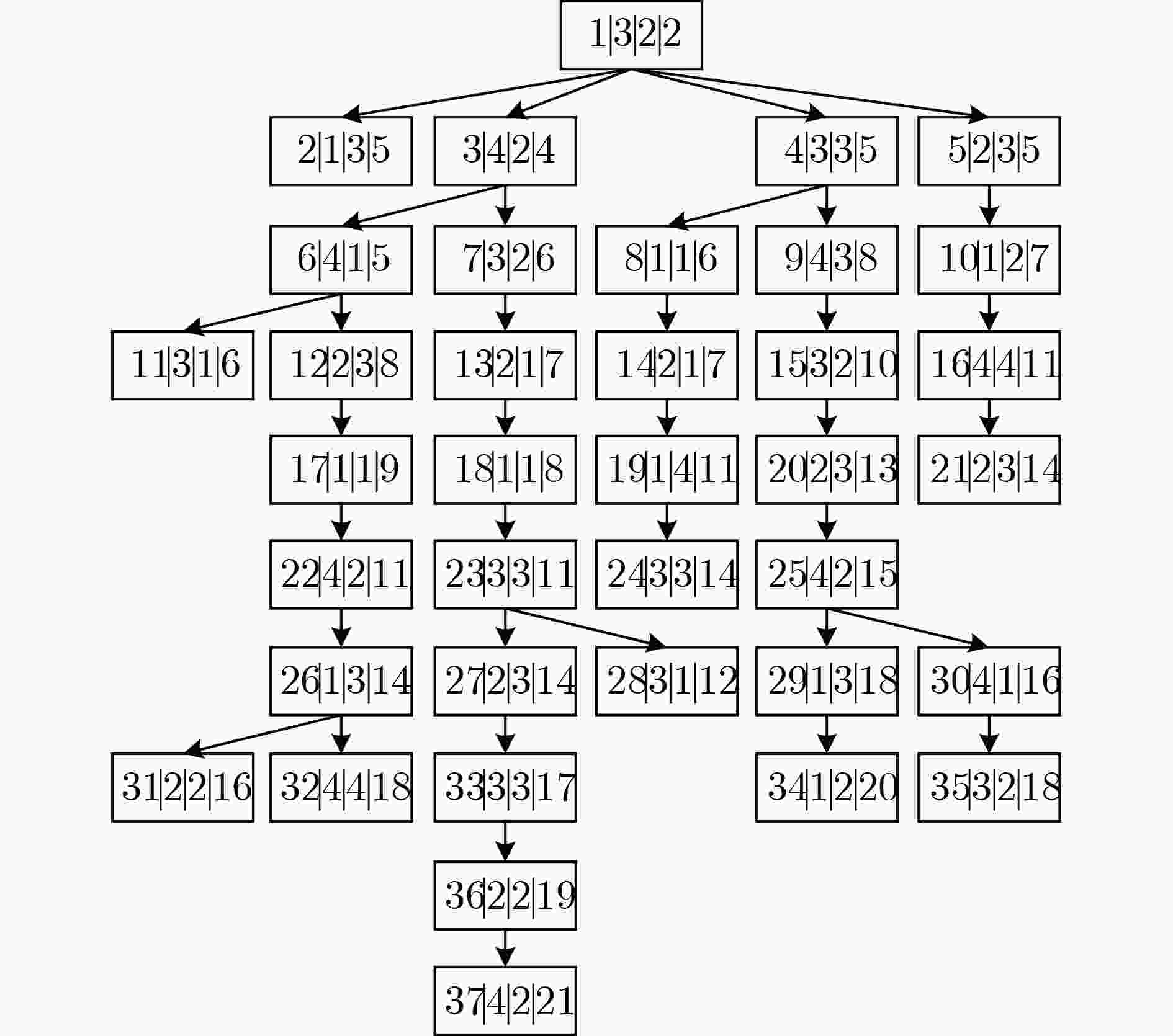
 下载:
下载:
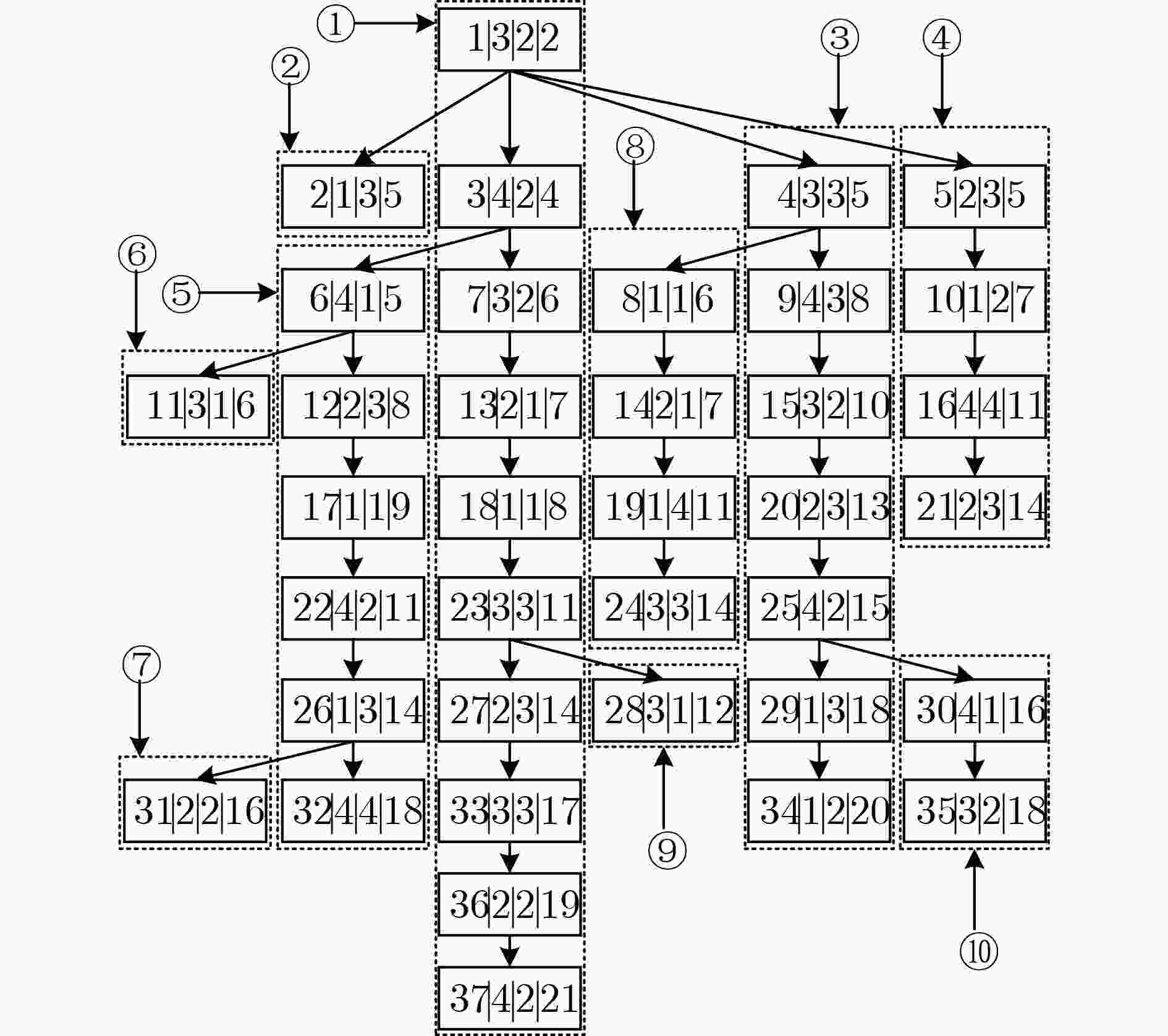


 下载:
下载:
