Design of Graph Convolutional Network Accelerator Based on Resistive Random Access Memory
-
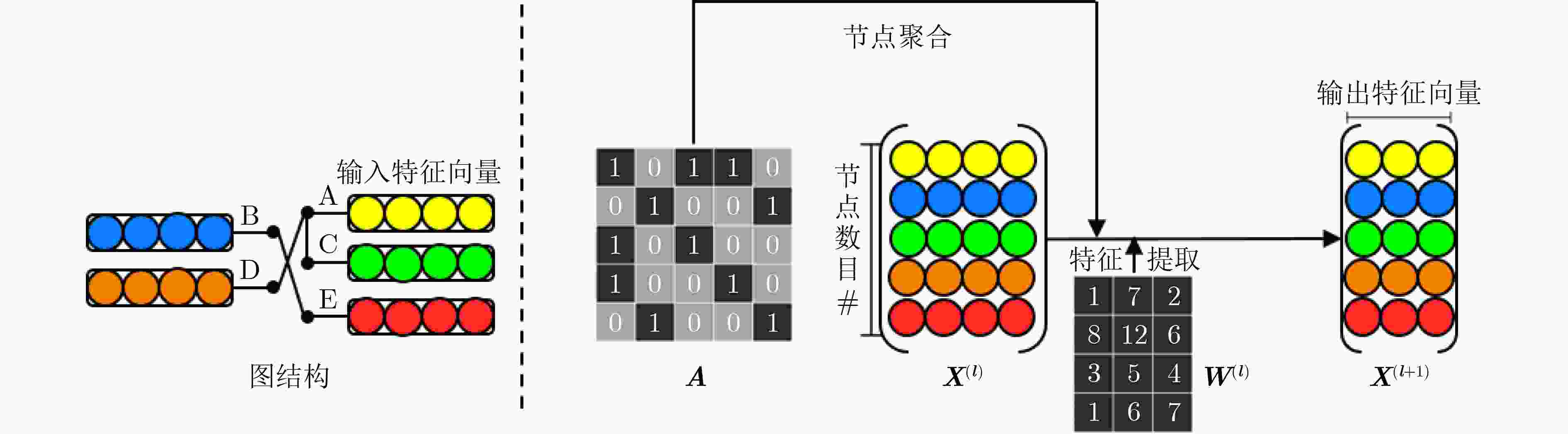
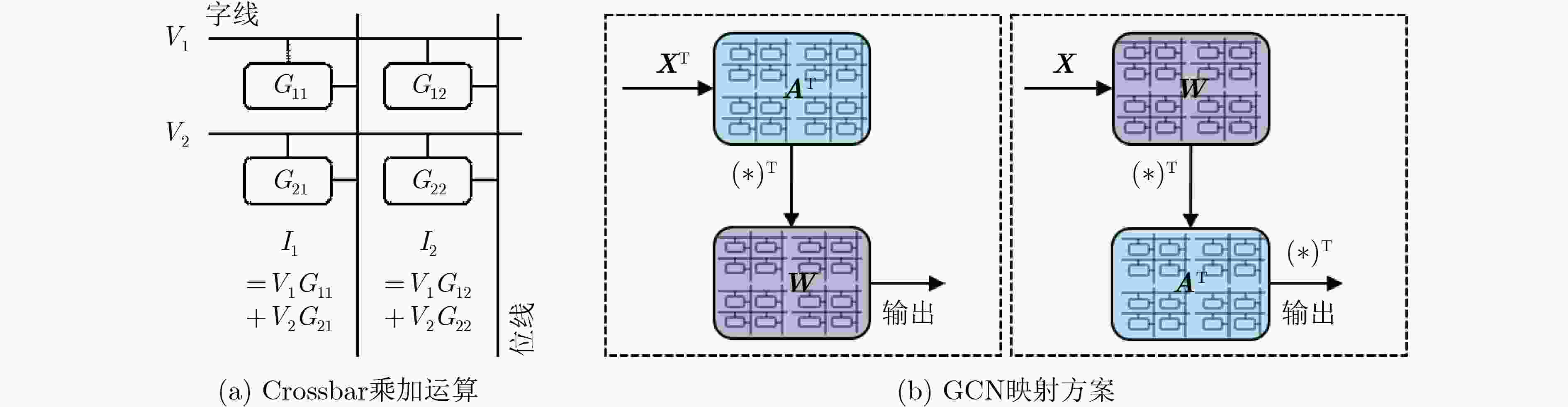
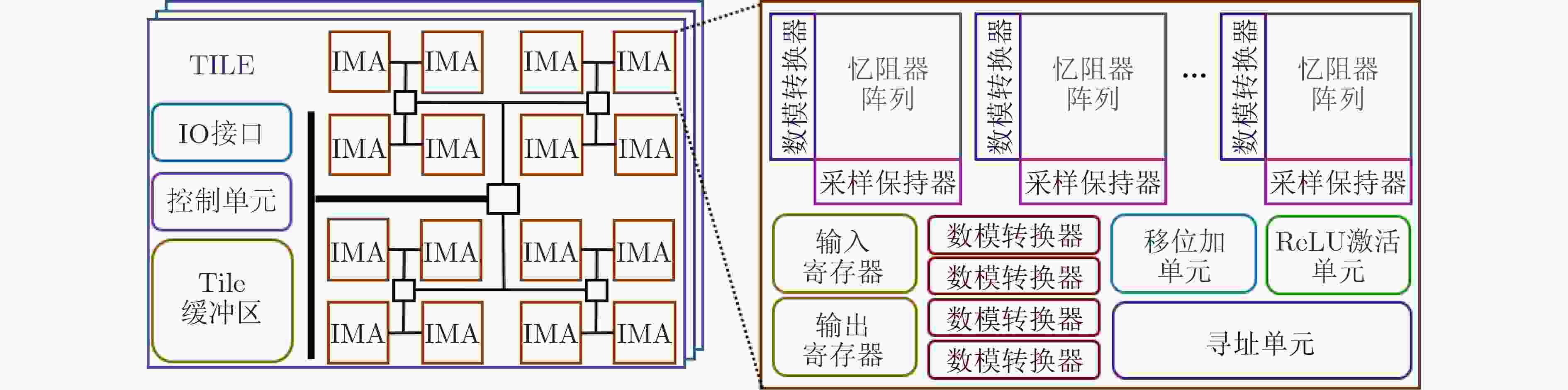
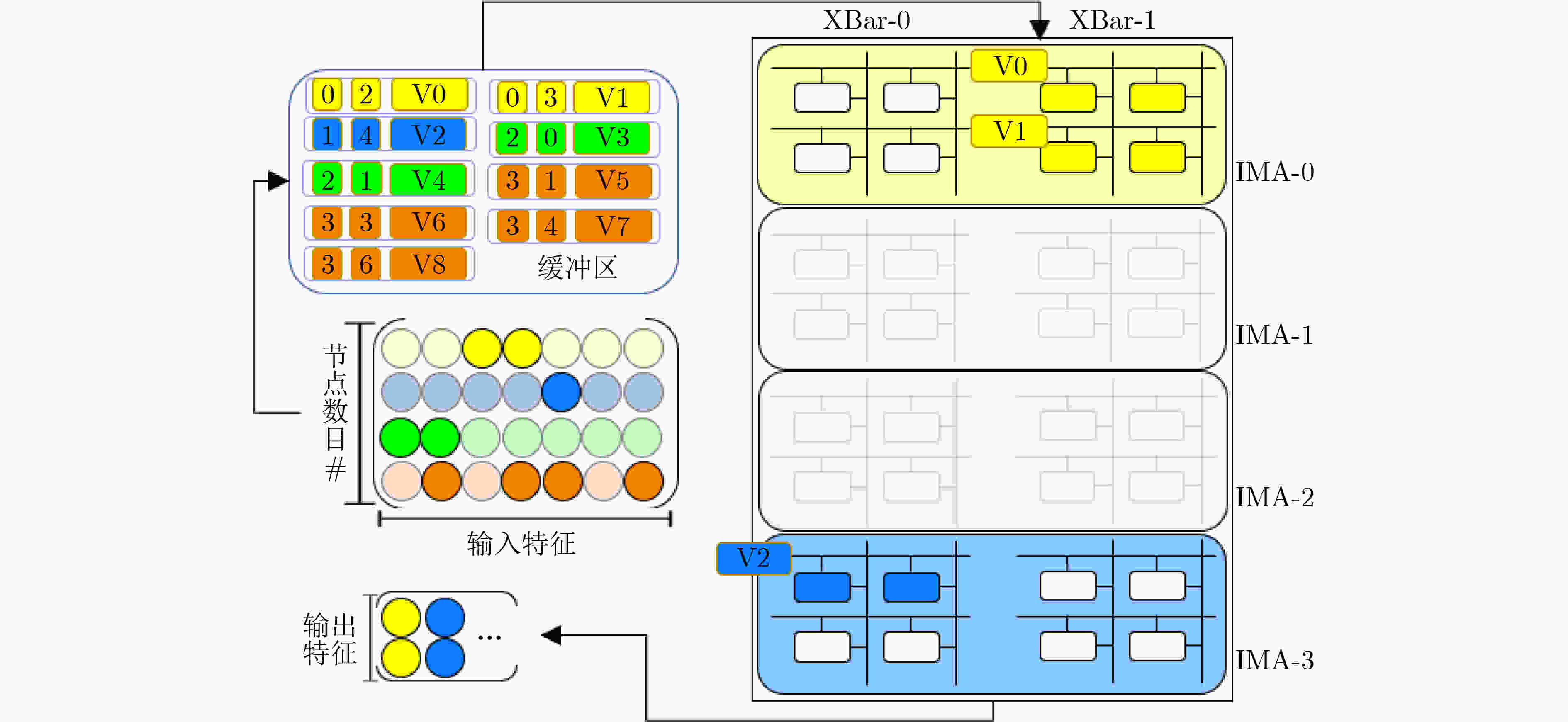
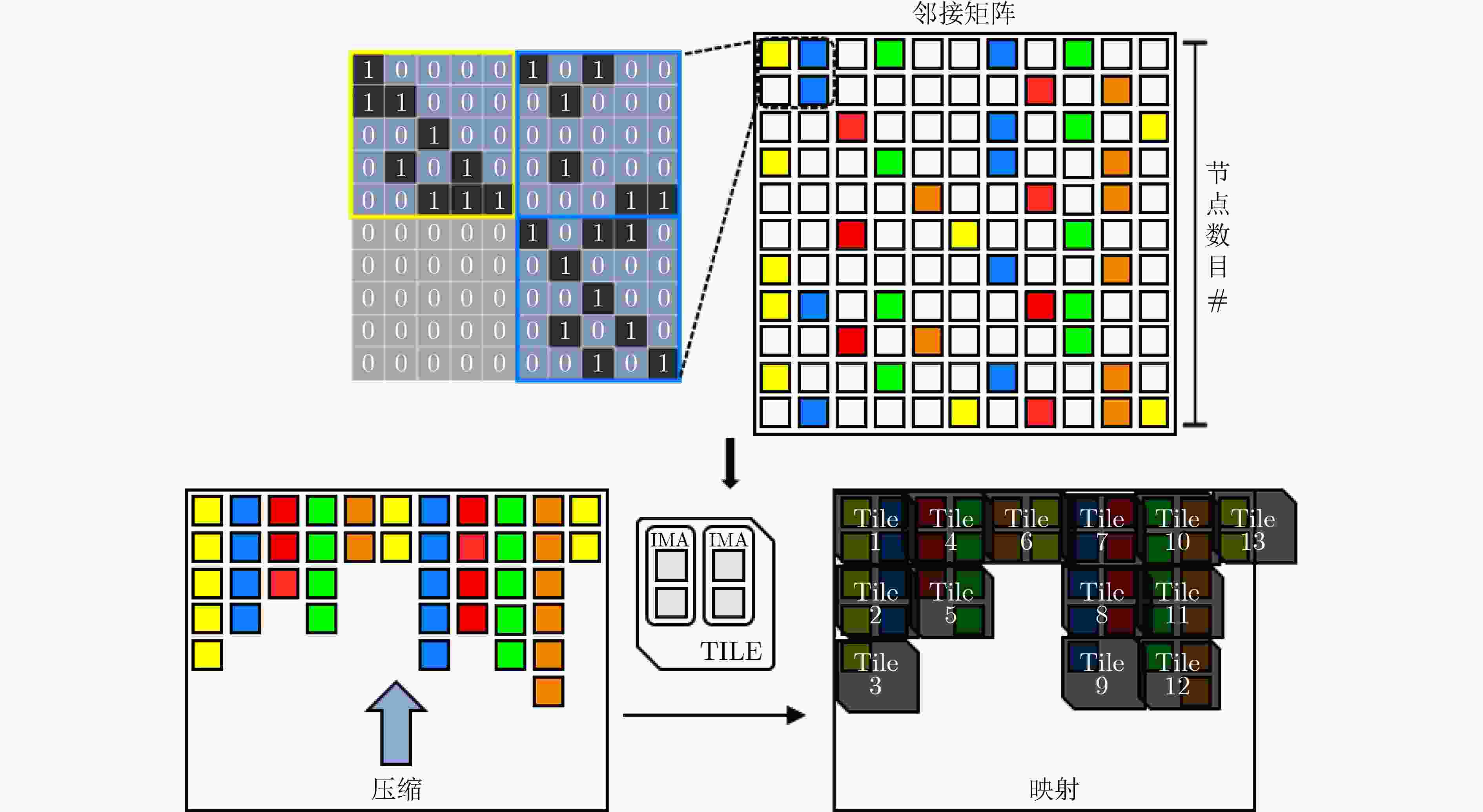
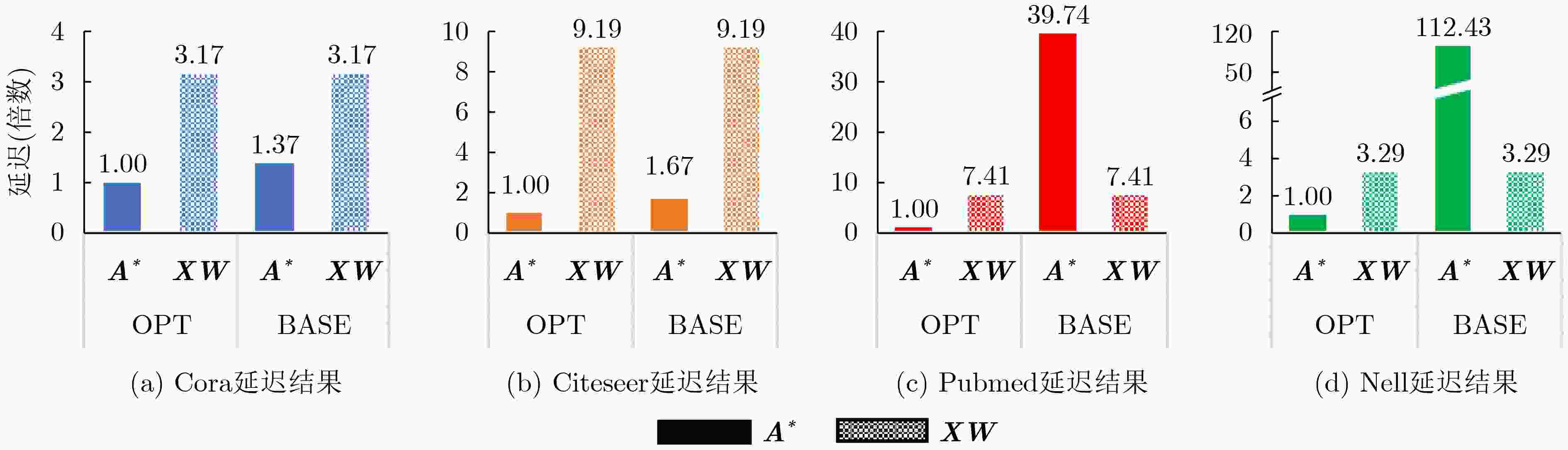
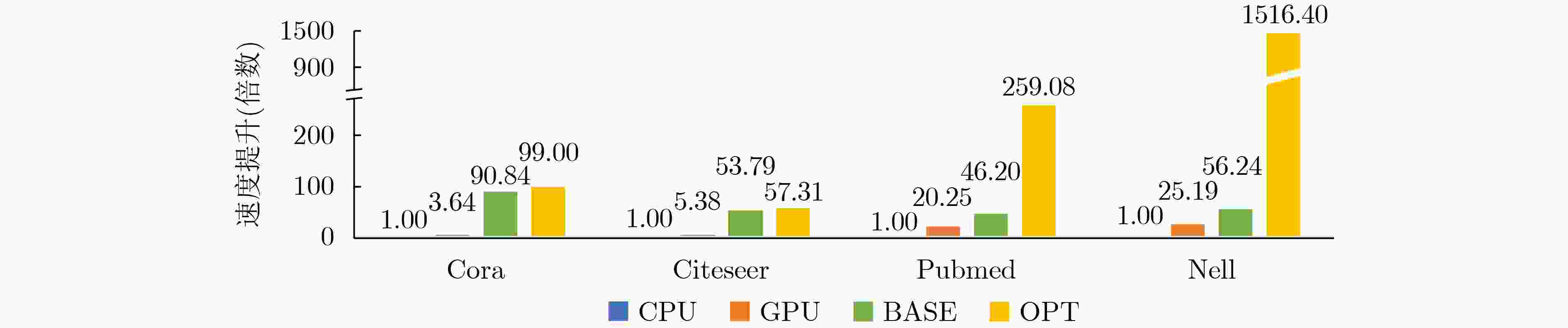
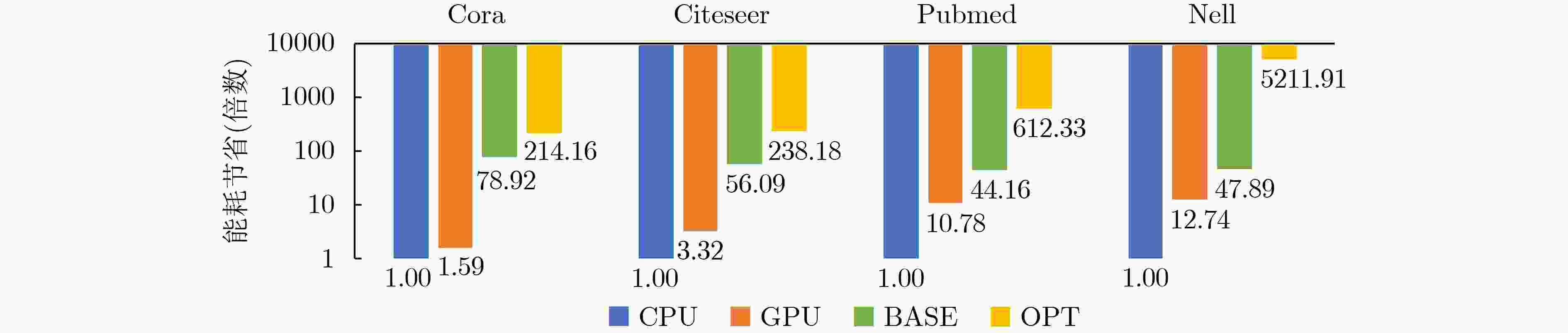
摘要: 图卷积神经网络(GCN)在社交网络、电子商务、分子结构推理等任务中的表现远超传统人工智能算法,在近年来获得广泛关注。与卷积神经网络(CNN)数据独立分布不同,图卷积神经网络更加关注数据之间特征关系的提取,通过邻接矩阵表示数据关系,因此其输入数据和操作数相比卷积神经网络而言都更加稀疏且存在大量数据传输,所以实现高效的GCN加速器是一个挑战。忆阻器(ReRAM)作为一种新兴的非易失性存储器,具有高密度、读取访问速度快、低功耗和存内计算等优点。利用忆阻器为CNN加速已经被广泛研究,但是图卷积神经网络极大的稀疏性会导致现有加速器效率低下,因此该文提出一种基于忆阻器交叉阵列的高效图卷积神经网络加速器,首先,该文分析GCN中不同操作数的计算和访存特征,提出权重和邻接矩阵到忆阻器阵列的映射方法,有效利用两种操作数的计算密集特征并避免访存密集的特征向量造成过高开销;进一步地,充分挖掘邻接矩阵的稀疏性,提出子矩阵划分算法及邻接矩阵的压缩映射方案,最大限度降低GCN的忆阻器资源需求;此外,加速器提供对稀疏计算支持,支持压缩格式为坐标表(COO)的特征向量输入,保证计算过程规则且高效地执行。实验结果显示,该文加速器相比CPU有483倍速度提升和1569倍能量节省;相比GPU也有28倍速度提升和168倍能耗节省。Abstract: Graph Convolutional Networks (GCNs) have superior performance in tasks such as social networking, ecommerce, molecular structure reasoning relative to traditional artificial intelligence algorithms, and have gained intensive attention in recent years. Unlike the independent distribution of data in Convolutional Neural Networks (CNNs), GCNs pay more attention to extract feature relationships between data, which is represented by the adjacency matrix. Therefore, the input data and operands in GCNs are much sparse and there are a large amount of data transmission, which makes it a challenge to implement an efficient GCN accelerator. Resistive Random Access Memory (ReRAM) as a new type of non-volatile memory has the advantages of high density, fast read access, near-zero leakage power and processing in-memory. Using ReRAM to accelerate CNNs has been widely studied. However, the extreme sparsity of GCNs makes it inefficiency to deploy on existing accelerators. In this work, a GCN accelerator based on ReRAM is proposed. First, the calculation and memory access characteristics of different operands in the GCN are analyzed, and a novel weight and adjacency matrix mapping policy is proposed by exploiting the intensive computing characteristic of weight and adjacency matrix, so that avoiding the excessive overhead caused by massive memory accesses; As for the extremely sparse adjacency matrix, a sub-matrix partitioning algorithm and a compression mapping scheme are proposed to minimize the GCN’s ReRAM resource requirements; Moreover, efficient processing on the sparse input feature vector with COOrdinate list (COO) compression format is provided by the proposed accelerator and the regular and efficient execution with the input feature vector are ensured. Experimental results show that the proposed work achieves 483 times speedup and 1569 times energy saving compared to CPU, and achieves 28 times speedup and consumes 168 times less energy over the GPU.
-
Key words:
- Processing in memory /
- New non-volatile memory /
- Graph Neural Network(GNN) /
- Accelerator
-
表 1 不同数据集密集度、体量和维度
Cora Citeseer Pubmed Nell 密集度(%) A 0.18 0.11 0.028 0.0073 X1 1.27 0.85 10.0 0.011 W 100 100 100 100 体量(%) A 65.01 47.10 97.44 92.12 X1 34.40 52.42 2.47 7.58 维度 节点数 2708 3327 19717 65755 特征数 1433 3703 500 5414 表 2 各数据集子矩阵划分粒度
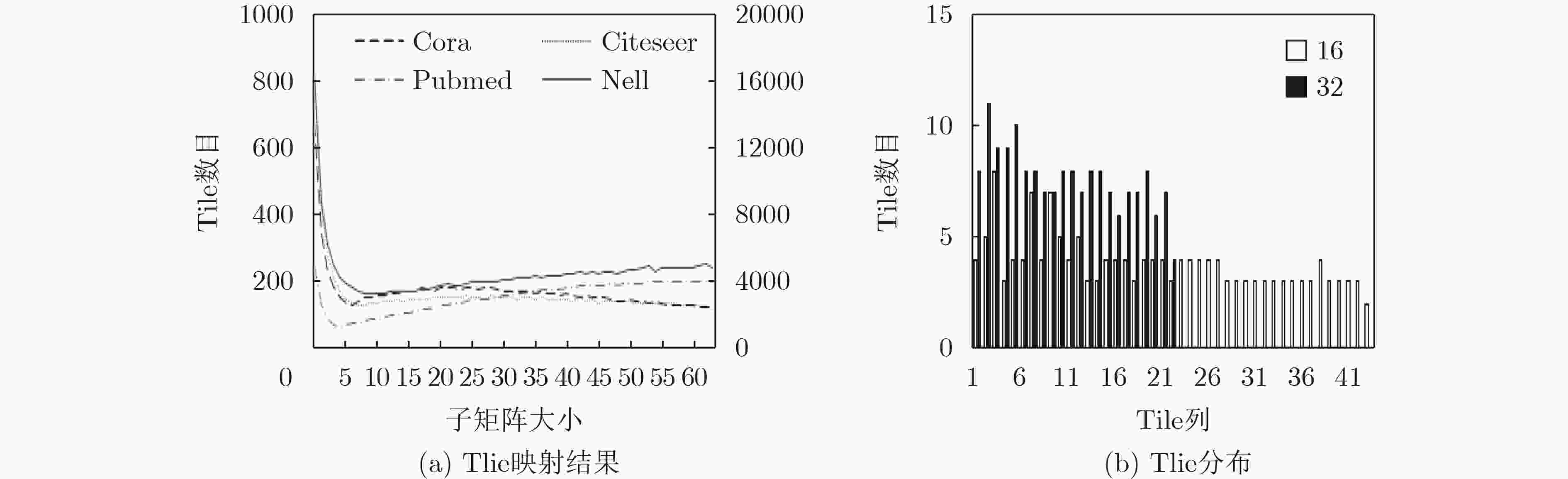
Cora Citeseer Pubmed Nell 子矩阵划分 62×62 64×64 5×5 10×10 Tile数目 116 115 1221 3194 基线Tile数目 121 169 6084 66049 Tile减少率(倍) 1.04 1.47 4.98 20.68 -
[1] KIPF T N and WELLING M. Semi-supervised classification with graph convolutional networks[C]. The 5th International Conference on Learning Representations, Toulon, France, 2017. [2] PARK H W, PARK S, and CHONG M. Conversations and medical news frames on twitter: Infodemiological study on COVID-19 in South Korea[J]. Journal of Medical Internet Research, 2020, 22(5): e18897. doi: 10.2196/18897 [3] SHI Chence, XU Minkai, ZHU Zhaocheng, et al. GraphAF: A flow-based autoregressive model for molecular graph generation[C]. The 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [4] YAN Mingyu, DENG Lei, HU Xing, et al. HyGCN: A GCN accelerator with hybrid architecture[C]. 2020 IEEE International Symposium on High Performance Computer Architecture, San Diego, USA, 2020: 15–29. [5] GENG Tong, LI Ang, SHI Runbin, et al. AWB-GCN: A graph convolutional network accelerator with runtime workload rebalancing[C]. The 53rd Annual IEEE/ACM International Symposium on Microarchitecture, Athens, Greece, 2020: 922–936. [6] LIANG Shengwen, WANG Ying, LIU Cheng, et al. EnGN: A high-throughput and energy-efficient accelerator for large graph neural networks[J]. IEEE Transactions on Computers, 2021, 70(9): 1511–1525. doi: 10.1109/TC.2020.3014632 [7] WONG H S P, LEE H Y, YU Shimeng, et al. Metal–oxide RRAM[J]. Proceedings of the IEEE, 2012, 100(6): 1951–1970. doi: 10.1109/JPROC.2012.2190369 [8] SHAFIEE A, NAG A, MURALIMANOHAR N, et al. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars[C]. The ACM/IEEE 43rd Annual International Symposium on Computer Architecture, Seoul, Korea, 2016: 14–26. [9] TANG Shibin, YIN Shouyi, ZHENG Shixuan, et al. AEPE: An area and power efficient RRAM crossbar-based accelerator for deep CNNs[C]. The IEEE 6th Non-Volatile Memory Systems and Applications Symposium, Hsinchu, China, 2017: 1–6. [10] CHI Ping, LI Shuangchen, XU Cong, et al. PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory[C]. The ACM/IEEE 43rd Annual International Symposium on Computer Architecture, Seoul, Korea, 2016: 27–39. [11] YANG T H, CHENG H Y, YANG C L, et al. Sparse ReRAM engine: Joint exploration of activation and weight sparsity in compressed neural networks[C]. The 46th Annual International Symposium on Computer Architecture, Phoenix, USA, 2019: 236–249. [12] SONG Linghao, ZHUO Youwei, QIAN Xuehai, et al. GraphR: Accelerating graph processing using ReRAM[C]. 2018 IEEE International Symposium on High Performance Computer Architecture, Vienna, Austria, 2018: 531–543. [13] CHALLAPALLE N, RAMPALLI S, SONG Linghao, et al. GaaS-X: Graph analytics accelerator supporting sparse data representation using crossbar architectures[C]. The 47th Annual International Symposium on Computer Architecture, Valencia, Spain, 2020: 433–445. [14] DAI Guohao, HUANG Tianhao, WANG Yu, et al. GraphSAR: A sparsity-aware processing-in-memory architecture for large-scale graph processing on ReRAMs[C]. The 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 2019: 120–126. [15] WANG Zhao, GUAN Yijin, SUN Guangyu, et al. GNN-PIM: A processing-in-memory architecture for graph neural networks[C]. The 13th Conference on Advanced Computer Architecture, Kunming, China, 2020: 73–86. [16] HE Yintao, WANG Ying, LIU Cheng, et al. TARe: Task-adaptive in-situ ReRAM computing for graph learning[C]. The 58th ACM/IEEE Design Automation Conference, San Francisco, USA, 2021: 577–582. [17] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386 [18] SEN P, NAMATA G, BILGIC M, et al. Collective classification in network data[J]. AI Magazine, 2008, 29(3): 93. doi: 10.1609/aimag.v29i3.2157 [19] CARLSON A, BETTERIDGE J, KISIEL B, et al. Toward an architecture for never-ending language learning[C]. The 24th AAAI Conference on Artificial Intelligence, Atlanta, America, 2010: 1306–1313. [20] SONG Linghao, QIAN Xuehai, LI Hai, et al. PipeLayer: A pipelined ReRAM-based accelerator for deep learning[C]. 2017 IEEE International Symposium on High Performance Computer Architecture, Austin, USA, 2017: 541–552. [21] ZHU Zhenhua, SUN Hanbo, QIU Kaizhong, et al. MNSIM 2.0: A behavior-level modeling tool for memristor-based neuromorphic computing systems[C]. The 2020 on Great Lakes Symposium on VLSI, Beijing, China, 2020: 83–88. [22] FEY Y and LENSSEN J E. Fast graph representation learning with PyTorch geometric[EB/OL]. https://arxiv.org/abs/1903.02428v3, 2019. [23] ABOU-RJEILI A and KARYPIS G. Multilevel algorithms for partitioning power-law graphs[C]. The 20th IEEE International Parallel & Distributed Processing Symposium, Rhodes, Greece, 2006: 10. -





 下载:
下载:



 下载:
下载:
