Quality Prediction for Injection Molding Product Based on Broad Learning System
-
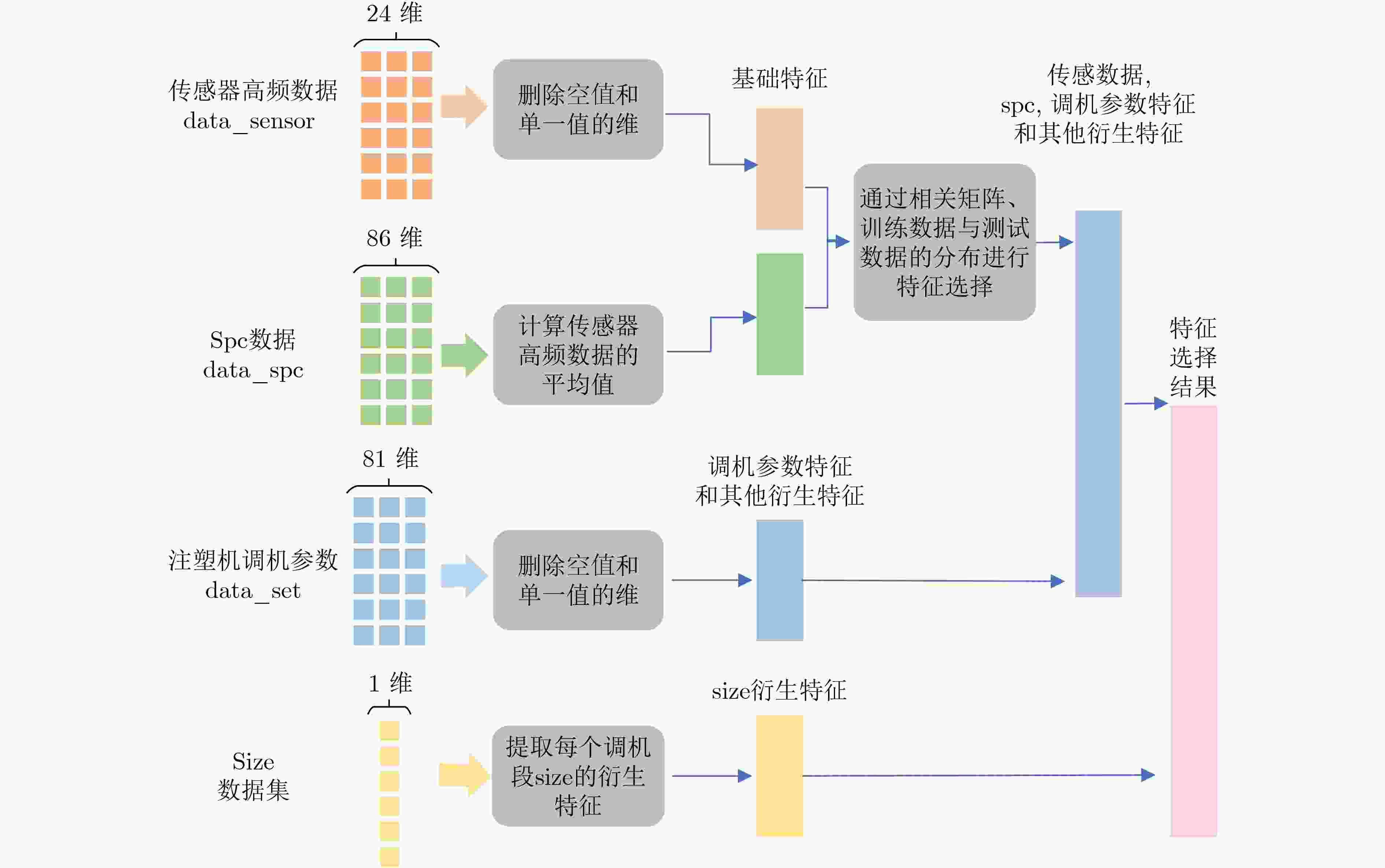
摘要: 在注塑成型工业中,产品质量自动监测一直是注塑工业智能化发展的核心问题。高品质和大规模的产品质量数据采集成本高昂,导致数据样本量少、不同类别样本数据不平衡,为注塑产品质量预测提出了更高的挑战。为此,该文提出一种基于宽度学习方法的注塑产品质量预测模型,以产品的3维尺寸为预测目标,在普通的宽度学习系统(BLS)中加入最小p范数来改进得到模型p范数宽度学习系统(pN-BLS),解决小样本和不平衡数据的问题,提高模型对离群点的检测性能。在第4届工业大数据竞赛任务2《注塑成型工艺的虚拟量测和调机优化》数据集中,将192个参数特征与预测目标进行相关分析,提取相关性高的基础特征17个,衍生特征4个和调机参数2个作为模型的输入。将16600条数据平均分为训练集和测试集各8300条,与支持向量机 (SVM)、最近邻算法 (KNN)、多层感知机 (MLP)和BLS进行对比实验,实验结果显示pN-BLS具有更快速和更准确的预测效果。在实际缺陷检测应用中,pN-BLS能更准确地预测异常数据,具有更高的鲁棒性。Abstract: Automatic monitoring of product quality has always been the core of intelligent development of injection molding industry. Practical factors like high cost of data collection, small sizes of sample and unbalanced sample categories require higher challenges for quality prediction of injection molded products. Therefore, a quality prediction model for injection molded products based on Broad Learning System (BLS) is proposed. Specifically, with the three-dimensional sizes of products as predicted targets, p-Norm is applied into the general BLS model to handle the problems of small samples and unbalanced data. The dataset from task two of the fourth industrial big data innovation competition is adopted. 192 parameter features are collected, among which 17 basic features, 4 derived features and 2 injection machine adjusting parameters are extracted as the input of the model via correlation analysis. The comparative experiments are then carried out between the proposed method and methods like Support Vector Machines (SVM), K-Nearest Neighbor (KNN), MultiLayer Perceptron (MLP) and BLS, with a respective sample size of 8300 data in the training and testing sets. Experimental results show that pN-BLS has the most accurate and fast effect of prediction. In practical defect detection applications, pN-BLS can predict abnormal data more accurately and has higher robustness.
-
表 1 特征选择结果
特征名 (单位) 特征类型 特征描述 size1 size2 size3 EL_CYC_TIME (s) 基础特征 周期时间 √ √ √ EL_IV_END_PRESS (MPa) 基础特征 切换压力 √ √ √ EL_PLST_BP_0 (MPa) 基础特征 第1段溶胶背压 √ √ √ EL_PLST_BP_1 (MPa) 基础特征 第2段溶胶背压 √ √ √ EL_PP_STG_POS_1 (mm) 基础特征 第2段保压终点位置 √ √ √ EL_PP_TIME (s) 基础特征 保压时间 √ √ √ ext_mold_temp_flt_3 (°C) 基础特征 模具温度中热水温度 √ √ √ MouldTemp10_mean (°C) 基础特征 模仁实际温度中公模温度传感器2的均值 √ √ √ MouldTemp11_mean (°C) 基础特征 模仁实际温度中公模温度传感器3的均值 √ √ √ MouldTemp13_mean (°C) 基础特征 模仁实际温度中母模温度传感器2的均值 √ √ √ MouldTemp14_mean (°C) 基础特征 模仁实际温度中母模温度传感器3的均值 √ √ √ MouldTemp2_mean (°C) 基础特征 模温机的实际温度传感器中的恒温2温度 √ √ √ MouldTemp4_mean (°C) 基础特征 模温机的实际温度传感器中的热水温度 √ √ √ Sensor1_mean (MPa) 基础特征 模内压力传感器1的均值 √ √ √ Sensor2_mean (MPa) 基础特征 模内压力传感器2的均值 √ √ √ Sensor8_mean (L/h) 基础特征 模温机水流流量计实际流量 √ √ √ inj_speed_4 (mm/s) 基础特征 第5段注塑速度 √ √ √ mdt_sp_0 (°C) 调机特征 机台参数的模具恒温温度 √ √ √ IJ_mean (MPa) 调机特征 喷嘴头的射出压力均值 √ √ √ size_set_Id_median (mm) 衍生特征 调机段中所有模次的size中位数 √ × √ Id_diff_ratio 衍生特征 表示当前模次的Id处在对应调机段的比率 × √ × Id_len 衍生特征 表示对应调机段的长度,即经历了多少模次产品 × √ × set_Id 衍生特征 该模次所处的调机段 √ √ √ 表 2 基于BLS的产品尺寸预测模型训练
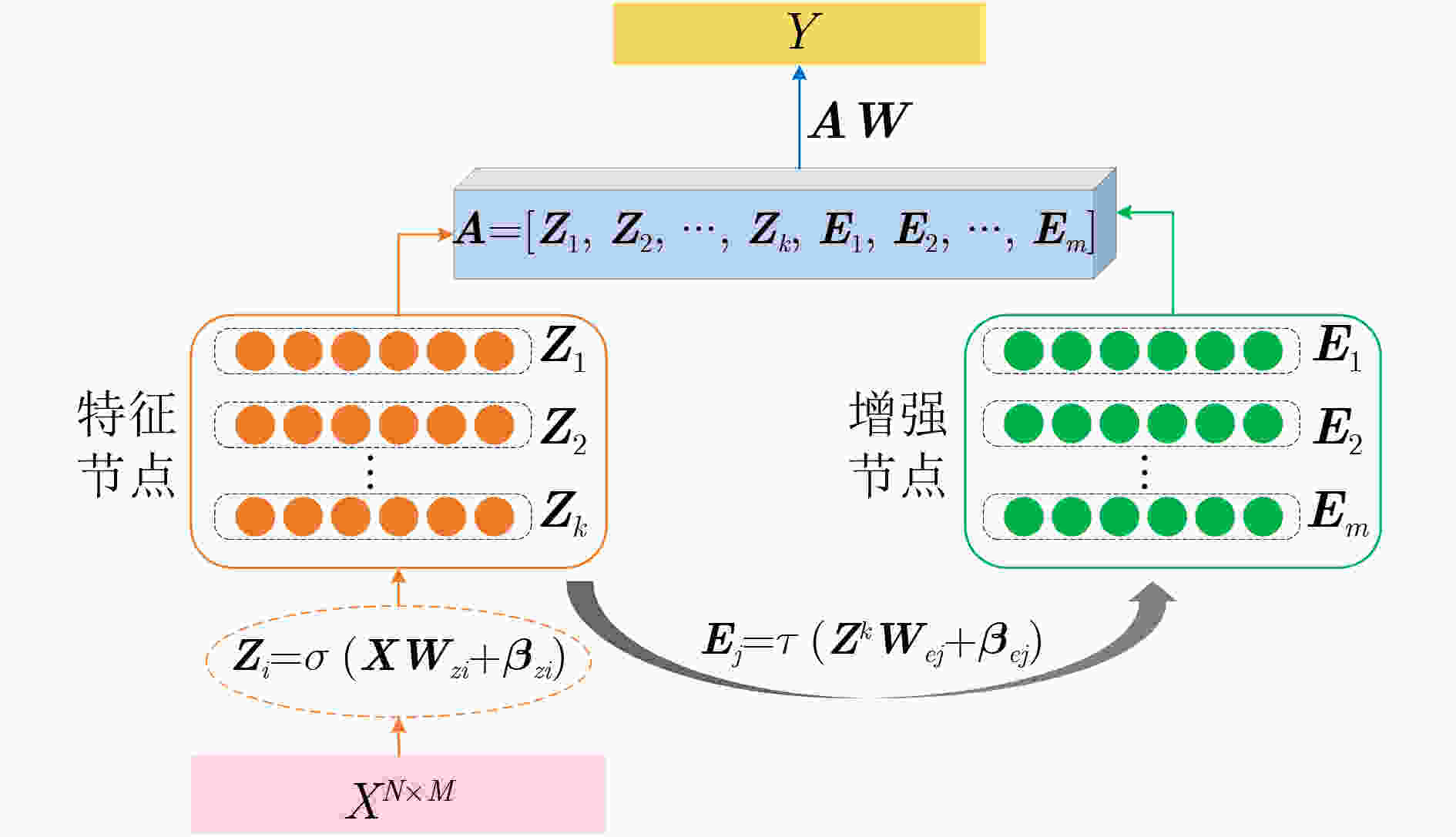
for $ i=1;i\le k $ do 随机产生特征层的参数矩阵$ {\boldsymbol{W}}_{zi} $, $ {\boldsymbol{\beta }}_{zi} $ 计算$ {\boldsymbol{Z}}_{i}=\sigma \left(\boldsymbol{X}{\cdot \boldsymbol{W}}_{zi}+{\boldsymbol{\beta }}_{zi}\right) $ end 获得$ {\boldsymbol{Z}}^{k}=[{\boldsymbol{Z}}_{1},{\boldsymbol{Z}}_{2},\cdots ,{\boldsymbol{Z}}_{k}] $ for $ j=1;j\le m $ do 随机产生增强层的参数矩阵$ {\boldsymbol{W}}_{ej} $, $ {\boldsymbol{\beta }}_{ej} $ 计算$ {\boldsymbol{E}}_{j}=\tau \left({\boldsymbol{Z}}^{k}\cdot {\boldsymbol{W}}_{ej}+{\boldsymbol{\beta }}_{ej}\right) $ end 获得 $ {\boldsymbol{E}}^{m}= $[$ {\boldsymbol{E}}_{1},{\boldsymbol{E}}_{2},{\cdots ,\boldsymbol{E}}_{m} $] 令$ \boldsymbol{A}=\left[{\boldsymbol{Z}}^{k},{\boldsymbol{E}}^{m}\right] $ 基于式(6)计算$ {\boldsymbol{A}}^{+} $ 计算并输出$ \boldsymbol{W}={\boldsymbol{A}}^{+}Y $ 表 3 基于pN-BLS的产品尺寸预测模型训练
for $ i=1;i\le k $ do 随机产生特征层的参数矩阵$ {\boldsymbol{W}}_{zi} $, $ {\boldsymbol{\beta }}_{zi} $ 计算$ {\boldsymbol{Z}}_{i}=\sigma \left(\boldsymbol{X}{\cdot \boldsymbol{W}}_{zi}+{\boldsymbol{\beta }}_{zi}\right) $ end 获得$ {\boldsymbol{Z}}^{k}=[{\boldsymbol{Z}}_{1},{\boldsymbol{Z}}_{2},\cdots ,{\boldsymbol{Z}}_{k}] $ for $ j=1;j\le m $ do 随机产生增强层的参数矩阵$ {\boldsymbol{W}}_{ej} $, $ {\boldsymbol{\beta }}_{ej} $ 计算$ {\boldsymbol{E}}_{j}=\tau \left({\boldsymbol{Z}}^{k}\cdot {\boldsymbol{W}}_{ej}+{\boldsymbol{\beta }}_{ej}\right) $ end 获得 $ {\boldsymbol{E}}^{m}= $[$ {\boldsymbol{E}}_{1},{\boldsymbol{E}}_{2},{\cdots ,\boldsymbol{E}}_{m} $] 令$ \boldsymbol{A}=\left[{\boldsymbol{Z}}^{k},{\boldsymbol{E}}^{m}\right] $ 随机产生初始矩阵$ \boldsymbol{W}\left(0\right) $ 计算 $ \widehat{Y}\left(0\right)=\boldsymbol{A}\cdot \boldsymbol{W}\left(0\right) $ for $ t=1;t\le h $ do 计算$ \mathrm{\delta }=Y-\widehat{Y}(t-1) $ 计算${\boldsymbol{\varLambda } }_{{\boldsymbol{W}}}={\rm{diag}}[{\left|{e}_{1}\right|}^{p-2},{\left|{e}_{2}\right|}^{p-2},\cdots ,{\left|{e}_{N}\right|}^{p-2}]$ 根据式(13)计算$ \boldsymbol{W}\left(t\right) $ 计算$ \widehat{Y}\left(t\right)=\boldsymbol{A}\cdot \boldsymbol{W}\left(t\right) $ end 输出$ \boldsymbol{W} $ 表 4 预测结果
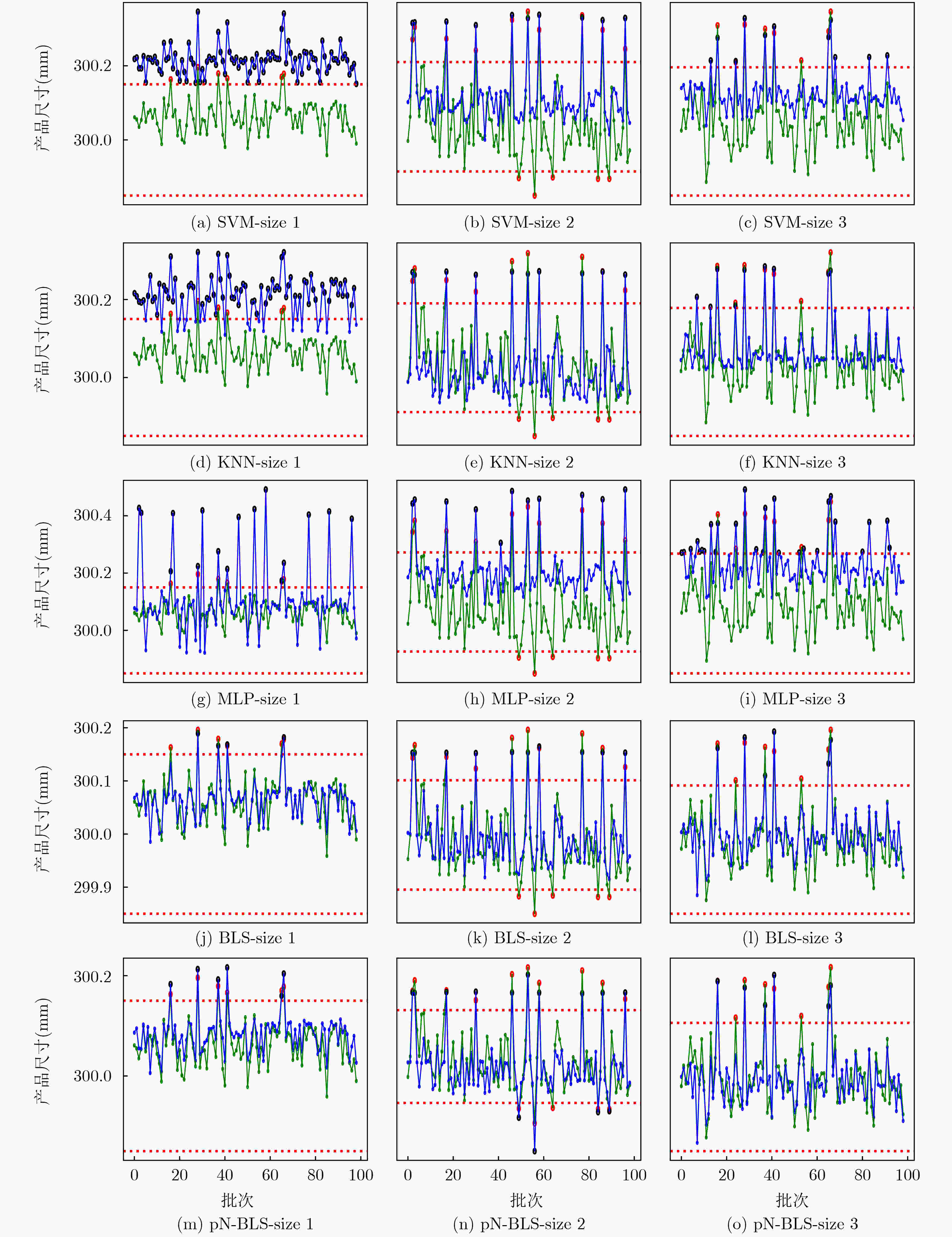
模型 size1 size2 size3 参数 MSE 参数 MSE 参数 MSE SVM (kernel=poly, degree=3) 0.044997 (kernel=poly, degree=3) 0.012554 (kernel=poly, degree=3) 0.011086 KNN (n-neighbors=99) 0.040116 (n-neighbors=99) 0.011213 (n-neighbors=99) 0.005682 MLP (N1=71, N2=5) 0.025351 (N1=83, N2=21) 0.0179505 (N1=43, N2=55) 0.020355 BLS (q=8, k=10, r=97) 0.000548 (q=10, k=10, r=95) 0.010706 (q=9, k=8, r=93) 0.000385 pN-BLS (p=0.1, q=10, k=10, r=83) 0.000196 (p=0.1, q=10, k=9, r=91) 0.010217 (p=0.1, q=10, k=7, r=45) 0.000187 (p=0.5, q=10, k=10, r=89) 0.000194 (p=0.5, q=2, k=10, r=17) 0.009877 (p=0.5, q=10, k=5, r=87) 0.000183 (p=1.0, q=10, k=5, r=93) 0.000191 (p=1.0, q=6, k=5, r=49) 0.008491 (p=1.0, q=10, k=6, r=59) 0.000181 (p=1.5, q=10, k=5, r=93) 0.000187 (p=1.5, q=6, k=10, r=69) 0.008483 (p=1.5, q=10, k=2, r=89) 0.000178 (p=2.0, q=10, k=10, r=91) 0.000191 (p=2.0, q=9, k=9, r=81) 0.008762 (p=2.0, q=10, k=4, r=41) 0.000179 (p=2.5, q=10, k=5, r=95) 0.0002 (p=2.5, q=3, k=7, r=69) 0.009113 (p=2.5, q=10, k=3, r=47) 0.000179 (p=3.0, q=6, k=10, r=79) 0.000229 (p=3.0, q=4, k=10, r=97) 0.009526 (p=3.0, q=10, k=4, r=89) 0.00018 (p=3.5, q=2, k=7, r=81) 0.00041 (p=3.5, q=2, k=9, r=97) 0.009588 (p=3.5, q=7, k=8, r=99) 0.00025 (p=4.0, q=6, k=4, r=7) 0.000512 (p=4.0, q=2, k=10, r=85) 0.011126 (p=4.0, q=10, k=3, r=93) 0.000382 表 5 预测时间(s)
模型 size1 size2 size3 SVM 0.16857 1.13388 0.415923 KNN 2.566221 2.965567 3.000962 MLP 0.004968 0.006944 0.008956 BLS 0.001953 0.001996 0.001956 pN-BLS 0.000074 0.000096 0.000081 -
[1] LI Xiaoli, HU Bin, and DU Ruxu. Predicting the parts weight in plastic injection molding using least squares support vector regression[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) , 2008, 38(6): 827–833. doi: 10.1109/TSMCC.2008.2001707 [2] OGORODNYK O, LYNGSTAD O V, LARSEN L, et al. Prediction of Width and Thickness of Injection Molded Parts Using Machine Learning Methods[M]. KISHITA Y, MATSUMOTO M, INOUE M, et al. EcoDesign and Sustainability I. Singapore: Springer, 2021: 455–469. [3] 郑生荣, 辛勇, 杨国泰, 等. 人工神经网络在注塑参数预测中的应用[J]. 塑料工业, 2003, 31(10): 26–28,33. doi: 10.3321/j.issn:1005-5770.2003.10.009ZHENG Shengrong, XIN Yong, YANG Guotai, et al. Application of artificial neural network in prediction of injection parameters[J]. China Plastics Industry, 2003, 31(10): 26–28,33. doi: 10.3321/j.issn:1005-5770.2003.10.009 [4] 王博, 蔡安江, 孟广慧, 等. 采用组合算法的注塑制品翘曲变形预测[J]. 西安交通大学学报, 2020, 54(8): 84–90. doi: 10.7652/xjtuxb202008011WANG Bo, CAI Anjiang, MENG Guanghui, et al. Warpage deformation prediction of injection products with combinatorial algorithm[J]. Journal of Xi’an Jiaotong University, 2020, 54(8): 84–90. doi: 10.7652/xjtuxb202008011 [5] 季宁, 张卫星, 于洋洋, 等. 基于径向基函数神经网络和多岛遗传算法的注射成型质量控制与预测[J]. 工程塑料应用, 2020, 48(4): 62–68. doi: 10.3969/j.issn.1001-3539.2020.04.011JI Ning, ZHANG Weixing, YU Yangyang, et al. Quality control and prediction of injection molding based on RBF neural network and MIGA[J]. Engineering Plastics Application, 2020, 48(4): 62–68. doi: 10.3969/j.issn.1001-3539.2020.04.011 [6] 宋建, 陈广森, 陈敬福, 等. 基于特征选择和贝叶斯优化LightGBM的注塑制品尺寸预测[J]. 工程塑料应用, 2021, 49(8): 54–60. doi: 10.3969/j.issn.1001-3539.2021.08.010SONG Jian, CHEN Guangsen, CHEN Jingfu, et al. Size prediction of injection molded products based on feature selection and Bayesian optimized LightGBM[J]. Engineering Plastics Application, 2021, 49(8): 54–60. doi: 10.3969/j.issn.1001-3539.2021.08.010 [7] 刘永兴, 唐小琦, 钟靖龙, 等. 基于LightGBM的非对称风险注塑成型产品尺寸预测模型[J/OL]. 中国机械工程. http://kns.cnki.net/kcms/detail/42.1294.TH.20210913.1448.002.html, 2022.LIU Yongxing, TANG Xiaoqi, ZHONG Jinglong, et al. Asymmetric risk injection molding product size prediction based on LightGBM[J/OL]. China Mechanical Engineering. http://kns.cnki.net/kcms/detail/42.1294.TH.20210913.1448.002.html, 2022. [8] LIU Jiahuan, GUO Fei, HUANG Gao, et al. Defect detection of injection molding products on small datasets using transfer learning[J]. Journal of Manufacturing Processes, 2021, 70: 400–413. doi: 10.1016/j.jmapro.2021.08.034 [9] KIM E, CHO S, LEE B, et al. Fault detection and diagnosis using self-attentive convolutional neural networks for variable-length sensor data in semiconductor manufacturing[J]. IEEE Transactions on Semiconductor Manufacturing, 2019, 32(3): 302–309. doi: 10.1109/TSM.2019.2917521 [10] KIM G, CHOI J G, KU M, et al. A multimodal deep learning-based fault detection model for a plastic injection molding process[J]. IEEE Access, 2021, 9: 132455–132467. doi: 10.1109/ACCESS.2021.3115665 [11] CHEN C L P and LIU Zhulin. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 10–24. doi: 10.1109/tnnls.2017.2716952 [12] CHEN C L P, LIU Zhulin, and FENG Shuang. Universal approximation capability of broad learning system and its structural variations[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(4): 1191–1204. doi: 10.1109/TNNLS.2018.2866622 [13] 郑云飞, 陈霸东. 基于最小p-范数的宽度学习系统[J]. 模式识别与人工智能, 2019, 32(1): 51–57. doi: 10.16451/j.cnki.issn1003-6059.201901007ZHENG Yunfei and CHEN Badong. Least p-norm based broad learning system[J]. Pattern Recognition and Artificial Intelligence, 2019, 32(1): 51–57. doi: 10.16451/j.cnki.issn1003-6059.201901007 -





 下载:
下载:


 下载:
下载:
