Hybrid Bi-directional Turbo Equalization for Underwater Acoustic Communications Based on Kalman Filter
-
摘要: 水声信道均衡中基于信道估计的均衡方法理论上具有更优的均衡性能,但较高的计算复杂度限制了算法的实际应用。针对这一问题,该文首先基于Kalman滤波和Turbo均衡提出一种迭代Kalman均衡器,实现了基于软符号的迭代信道估计与迭代Kalman均衡,且复杂度较常规方法降低约1个数量级。其次,针对单一均衡算法和单一方向Turbo均衡器存在的误差传递现象,设计了基于迭代Kalman均衡器与改进成比例归一化LMS (IPNLMS)自适应均衡器相结合的混合双向Turbo均衡器,提高了自适应均衡器的收敛速度和均衡性能,并通过双向均衡结构带来的增益改善了符号估计误差传递的现象。理论分析与仿真实验验证了该文算法的有效性。Abstract: In underwater acoustic channel equalization, the channel estimation-based equalization has better performance theoretically, but the high computational complexity limits its practical applications. To solve this problem, an iterative Kalman equalizer based on Kalman filter and Turbo equalization is proposed firstly, which realizes iterative channel estimation and iterative Kalman equalization based on soft symbols generated by the channel decoder, and the complexity is about one order of magnitude lower than that of conventional methods. Secondly, aiming at the error transmission of a single equalization algorithm and single direction Turbo equalizer structure, a hybrid bi-directional Turbo equalizer based on iterative Kalman equalizer and Improved Proportional Normalized LMS (IPNLMS) adaptive equalizer is designed, which improves the convergence speed and equalization performance of the adaptive equalizer, and reduces the error transmission through bi-directional equalization gain. The proposed hybrid bi-directional Turbo equalization for underwater acoustic communications based on the Kalman filter is verified by theoretical analysis and simulation.
-
表 1 仿真系统实验参数设置
参数 参数值 采样频率 96 kHz 中心频率 12 kHz 信号带宽 6 kHz 符号速率 6×103 symbols/s 调制方式 QPSK 编码方式 CONV 编码码率 0.5 训练数据长度 200 symbols 表 2 均衡器算法复杂度比较
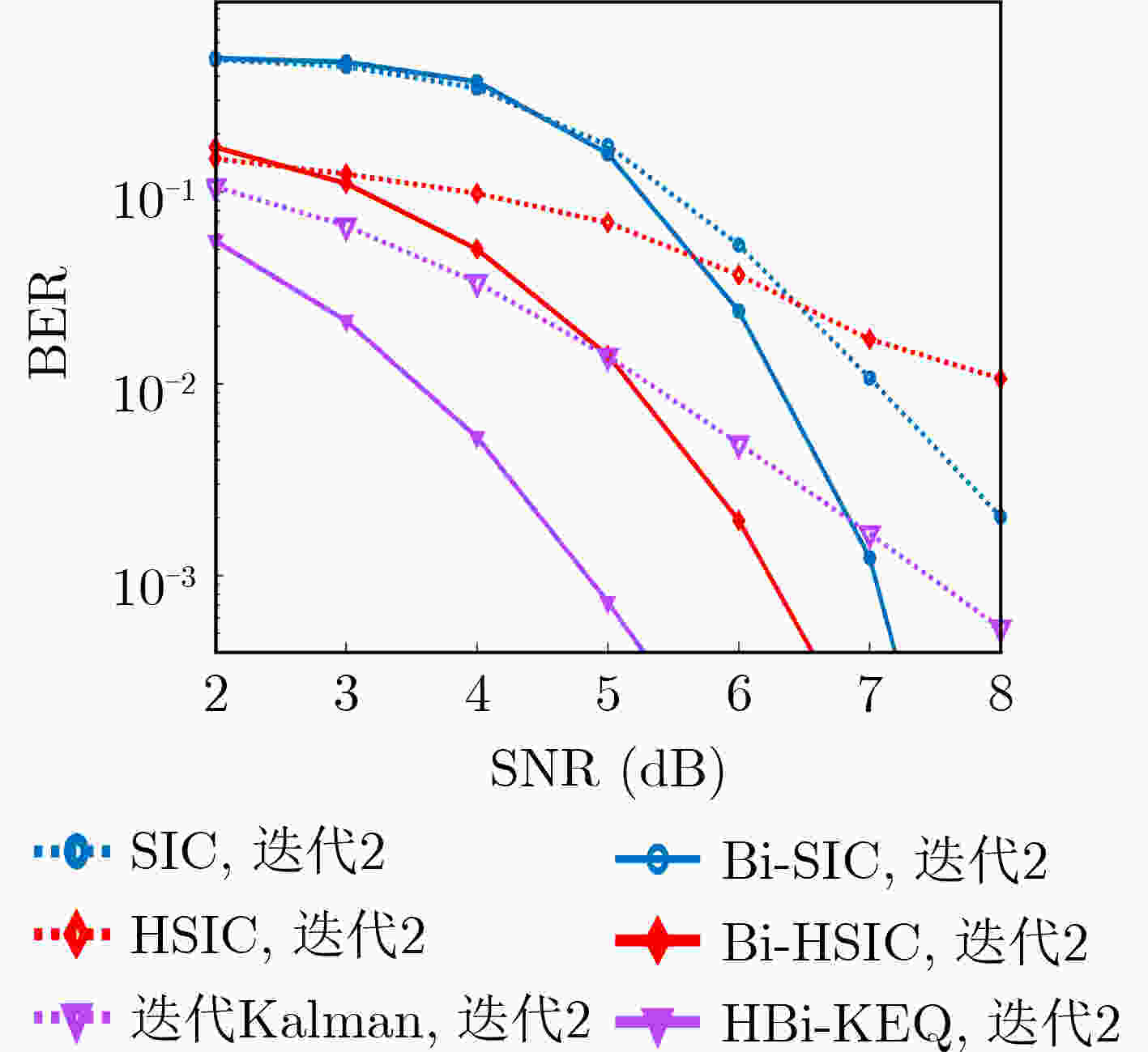
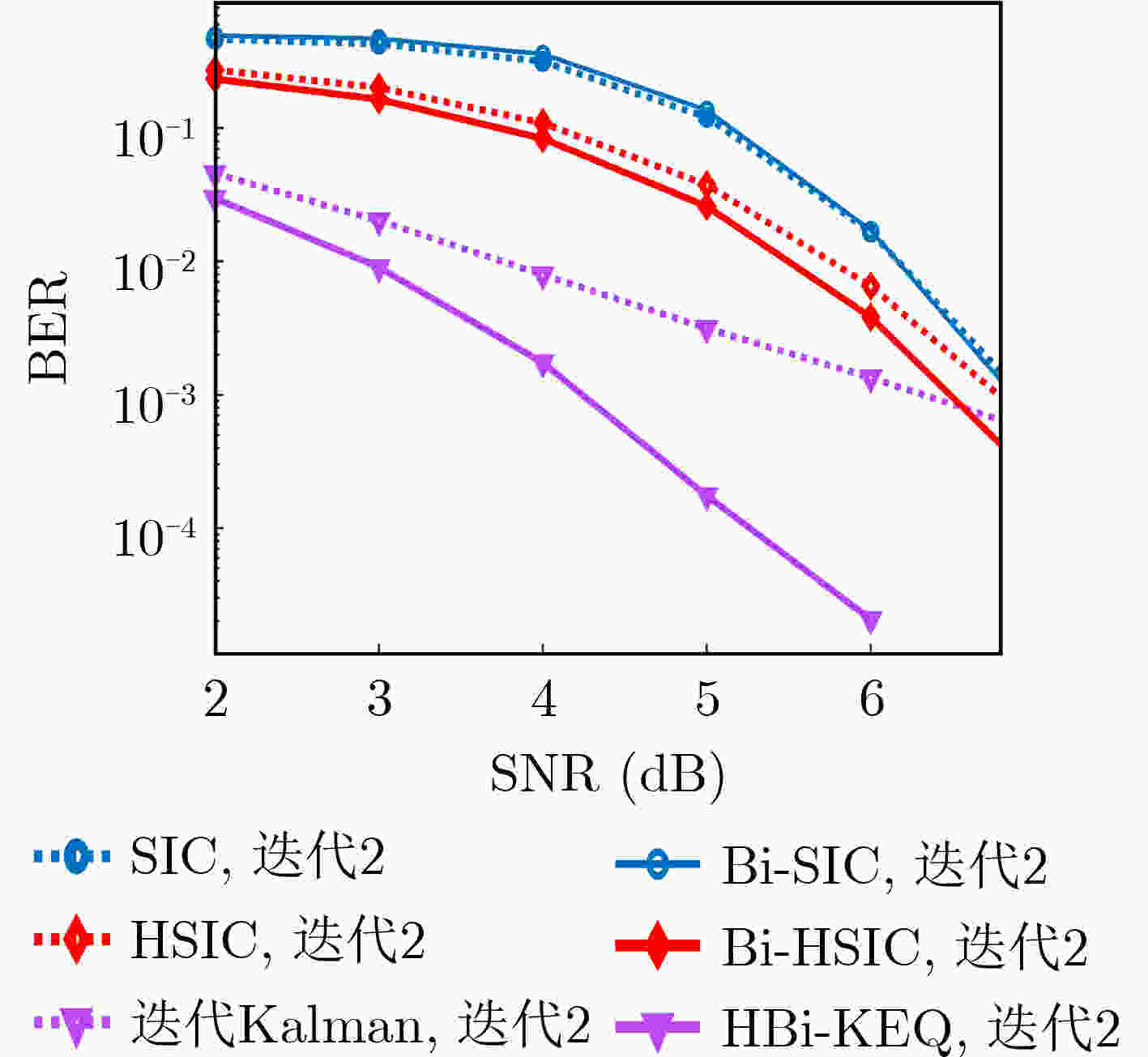
均衡器 计算复杂度 SIC $ \mathcal{O}(5N{\text{ + 3}}) $ Bi-SIC $ \mathcal{O}(10N{\text{ + 6}}) $ HSIC $ \mathcal{O}({N^3}) $ Bi-HSIC $ \mathcal{O}({N^3} + 5N + 3) $ 迭代Kalman $ \mathcal{O}(4{N^2} + 4N + 1) $ HBi-KEQ $ \mathcal{O}(4{N^2} + 9N + 4) $ -
[1] HUANG Jianguo, WANG Han, HE Chengbing, et al. Underwater acoustic communication and the general performance evaluation criteria[J]. Frontiers of Information Technology & Electronic Engineering, 2018, 19(8): 951–971. doi: 10.1631/FITEE.1700775 [2] STOJANOVIC M, CATIPOVIC J A, and PROAKIS J G. Phase-coherent digital communications for underwater acoustic channels[J]. IEEE Journal of Oceanic Engineering, 1994, 19(1): 100–111. doi: 10.1109/48.289455 [3] ZHANG Yi, VENKATESAN R, DOBRE O A, et al. Efficient estimation and prediction for sparse time-varying underwater acoustic channels[J]. IEEE Journal of Oceanic Engineering, 2020, 45(3): 1112–1125. doi: 10.1109/JOE.2019.2911446 [4] SONG Aijun, BADIEY M, MCDONALD V K, et al. Time reversal receivers for high data rate acoustic multiple-input–multiple-output communication[J]. IEEE Journal of Oceanic Engineering, 2011, 36(4): 525–538. doi: 10.1109/JOE.2011.2166660 [5] PELEKANAKIS K and CHITRE M. New sparse adaptive algorithms based on the natural gradient and the L0-norm[J]. IEEE Journal of Oceanic Engineering, 2013, 38(2): 323–332. doi: 10.1109/JOE.2012.2221811 [6] CHEN Zhenrui, WANG Jintao, and ZHENG Y R. Frequency-domain Turbo equalization with iterative channel estimation for MIMO underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2017, 42(3): 711–721. doi: 10.1109/JOE.2016.2600106 [7] WANG Longbao, TAO Jun, and ZHENG Y R. Single-carrier frequency-domain Turbo equalization without cyclic prefix or zero padding for underwater acoustic communications[J]. The Journal of the Acoustical Society of America, 2012, 132(6): 3809–3817. doi: 10.1121/1.4763987 [8] YANG Zengli and ZHENG Y R. Iterative channel estimation and Turbo equalization for multiple-input multiple-output underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2016, 41(1): 232–242. doi: 10.1109/JOE.2015.2398731 [9] LAWRENCE R and KAUFMAN H. The Kalman filter for the equalization of a digital communications channel[J]. IEEE Transactions on Communication Technology, 1971, 19(6): 1137–1141. doi: 10.1109/TCOM.1971.1090786 [10] ROY S and DUMAN T M. Soft input soft output Kalman equalizer for MIMO frequency selective fading channels[J]. IEEE Transactions on Wireless Communications, 2007, 6(2): 506–514. doi: 10.1109/TWC.2007.05175 [11] PARK S and CHOI S. Iterative equalizer based on Kalman filtering and smoothing for MIMO-ISI channels[J]. IEEE Transactions on Signal Processing, 2015, 63(19): 5111–5120. doi: 10.1109/TSP.2015.2457399 [12] TAO Jun, WU Yanbo, WU Qisong, et al. Kalman filter based equalization for underwater acoustic communications[C]. OCEANS 2019, Marseille, France, 2019: 1–5. [13] DOUILLARD C, JÉZÉQUEL M, BERROU C, et al. Iterative correction of intersymbol interference: Turbo-equalization[J]. European Transactions on Telecommunications, 1995, 6(5): 507–511. doi: 10.1002/ett.4460060506 [14] LI Xin and WONG T F. Turbo equalization with nonlinear Kalman filtering for time-varying frequency-selective fading channels[J]. IEEE Transactions on Wireless Communications, 2007, 6(2): 691–700. doi: 10.1109/TWC.2007.05352 [15] YANG Binbin, YAN Shefeng, XU Lijun, et al. Hybrid Turbo equalization based on Kalman filter for underwater acoustic communications[C]. 2021 IEEE International Conference on Signal Processing, Communications and Computing, Xi’an, China, 2021: 1–6. [16] 杨光, 丁寒雪, 郭庆华, 等. 基于叠加训练序列和低复杂度频域Turbo均衡的时变水声信道估计和均衡[J]. 电子与信息学报, 2021, 43(3): 850–856. doi: 10.11999/JEIT200315YANG Guang, DING Hanxue, GUO Qinghua, et al. Estimation and equalization of time-varying underwater acoustic channel based on superimposed training and low-complexity Turbo equalization in frequency domain[J]. Journal of Electronics &Information Technology, 2021, 43(3): 850–856. doi: 10.11999/JEIT200315 [17] 奚钧壹, 鄢社锋, 徐立军, 等. 水声通信系统中双向turbo均衡算法[J]. 声学学报, 2018, 43(5): 771–778. doi: 10.15949/j.cnki.0371-0025.2018.05.006XI Junyi, YAN Shefeng, XU Lijun, et al. Bidirectional turbo equalization for underwater acoustic communications[J]. Acta Acustica, 2018, 43(5): 771–778. doi: 10.15949/j.cnki.0371-0025.2018.05.006 [18] WANG Zhizhan, LI Yuzhou, WANG Chengcai, et al. A-OMP: An adaptive OMP algorithm for underwater acoustic OFDM channel estimation[J]. IEEE Wireless Communications Letters, 2021, 10(8): 1761–1765. doi: 10.1109/LWC.2021.3079225 [19] MARQUES E C, MACIEL N, NAVINER L, et al. A review of sparse recovery algorithms[J]. IEEE Access, 2019, 7: 1300–1322. doi: 10.1109/ACCESS.2018.2886471 [20] NEEDELL D and VERSHYNIN R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317–334. doi: 10.1007/s10208-008-9031-3 [21] XI Junyi, YAN Shefeng, and XU Lijun. Direct-adaptation based bidirectional Turbo equalization for underwater acoustic communications: Algorithm and undersea experimental results[J]. The Journal of the Acoustical Society of America, 2018, 143(5): 2715–2728. doi: 10.1121/1.5036730 [22] TAO Jun, WU Jingxian, ZHENG Y R, et al. Enhanced MIMO LMMSE Turbo equalization: Algorithm, simulations, and undersea experimental results[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3813–3823. doi: 10.1109/TSP.2011.2147782 -





 下载:
下载:



 下载:
下载:
