Two-dimensional Frequency Hopping Communication System and Performance Analysis Based on Discrete Fractional Fourier Transform
-
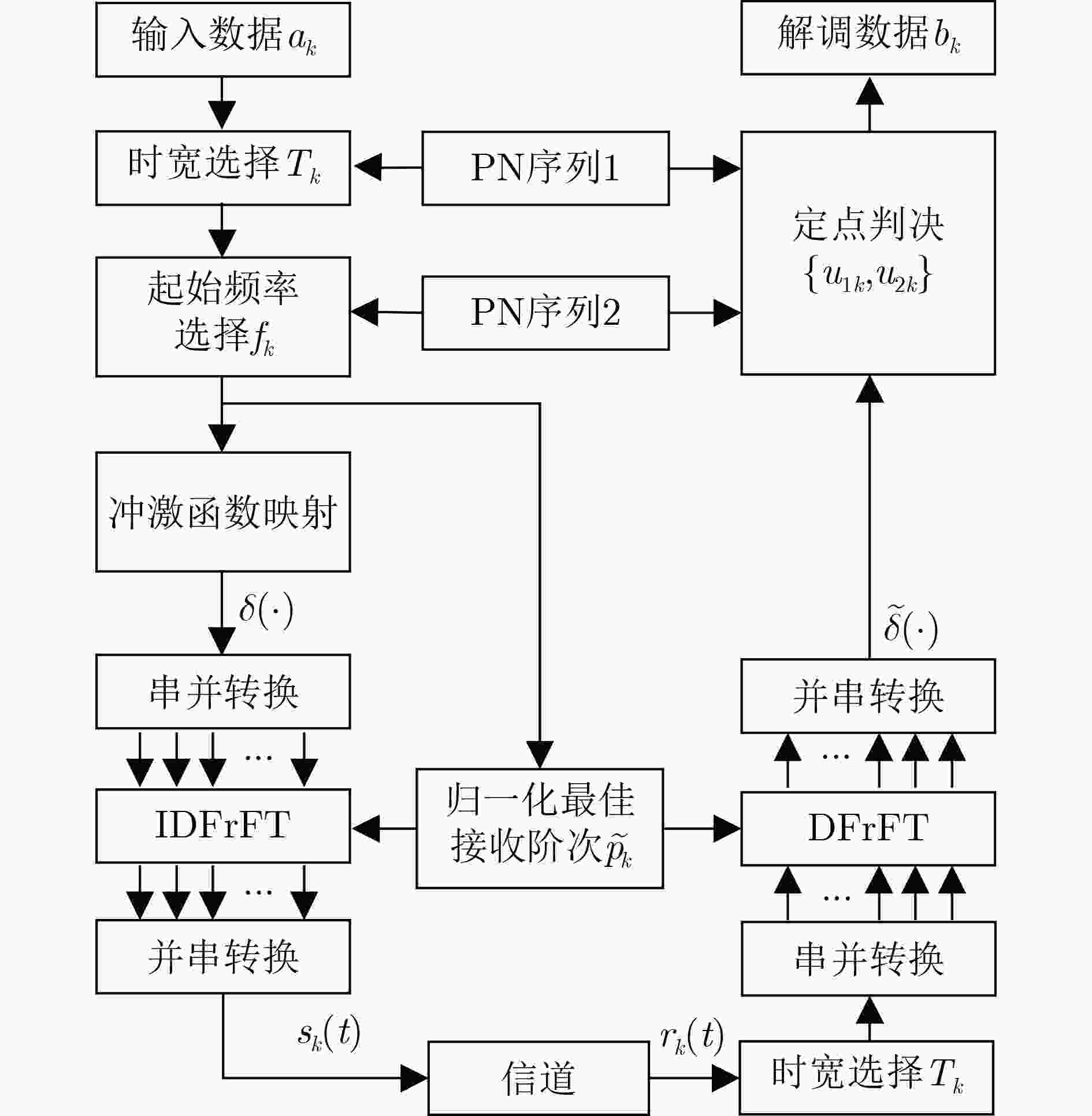
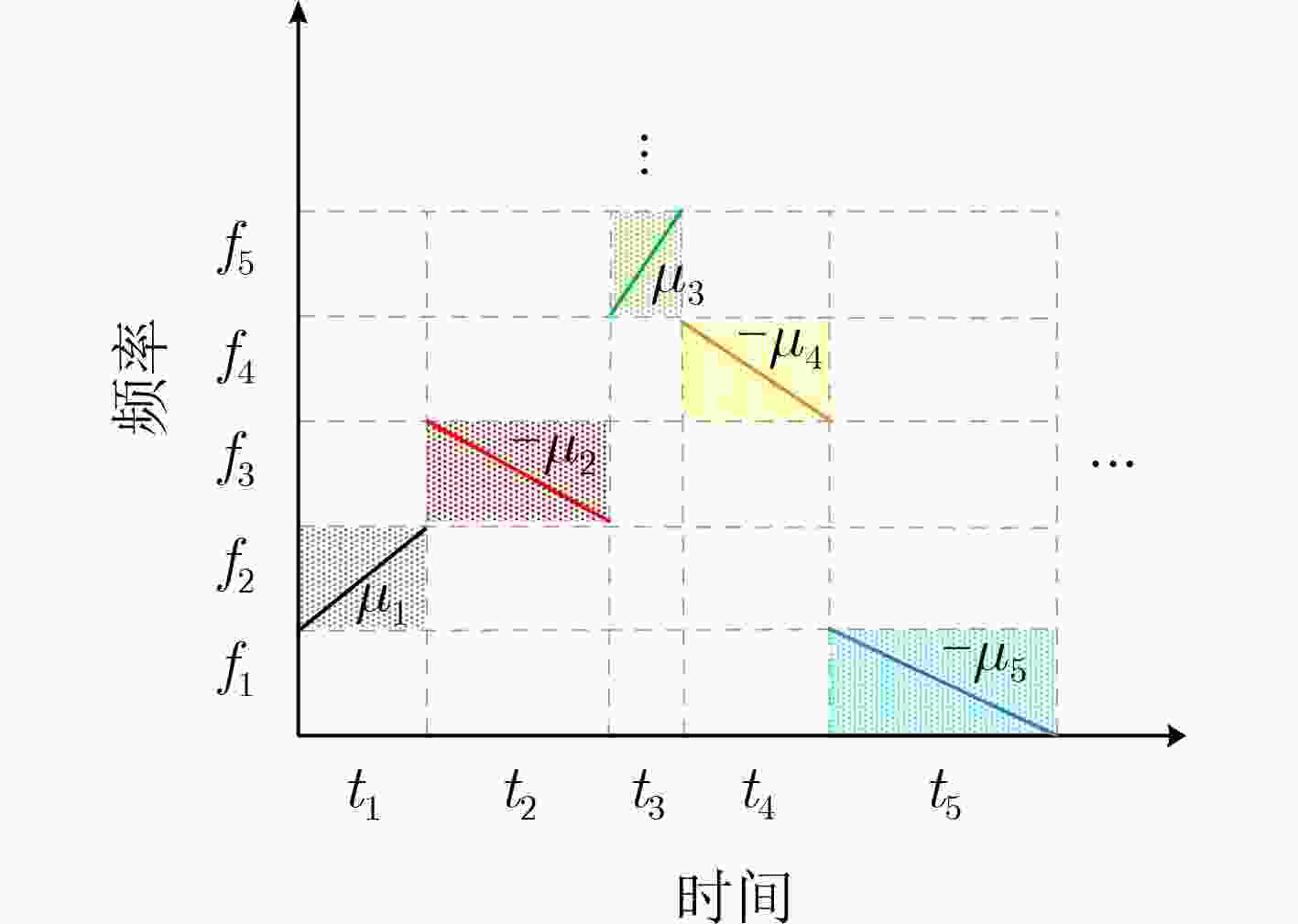
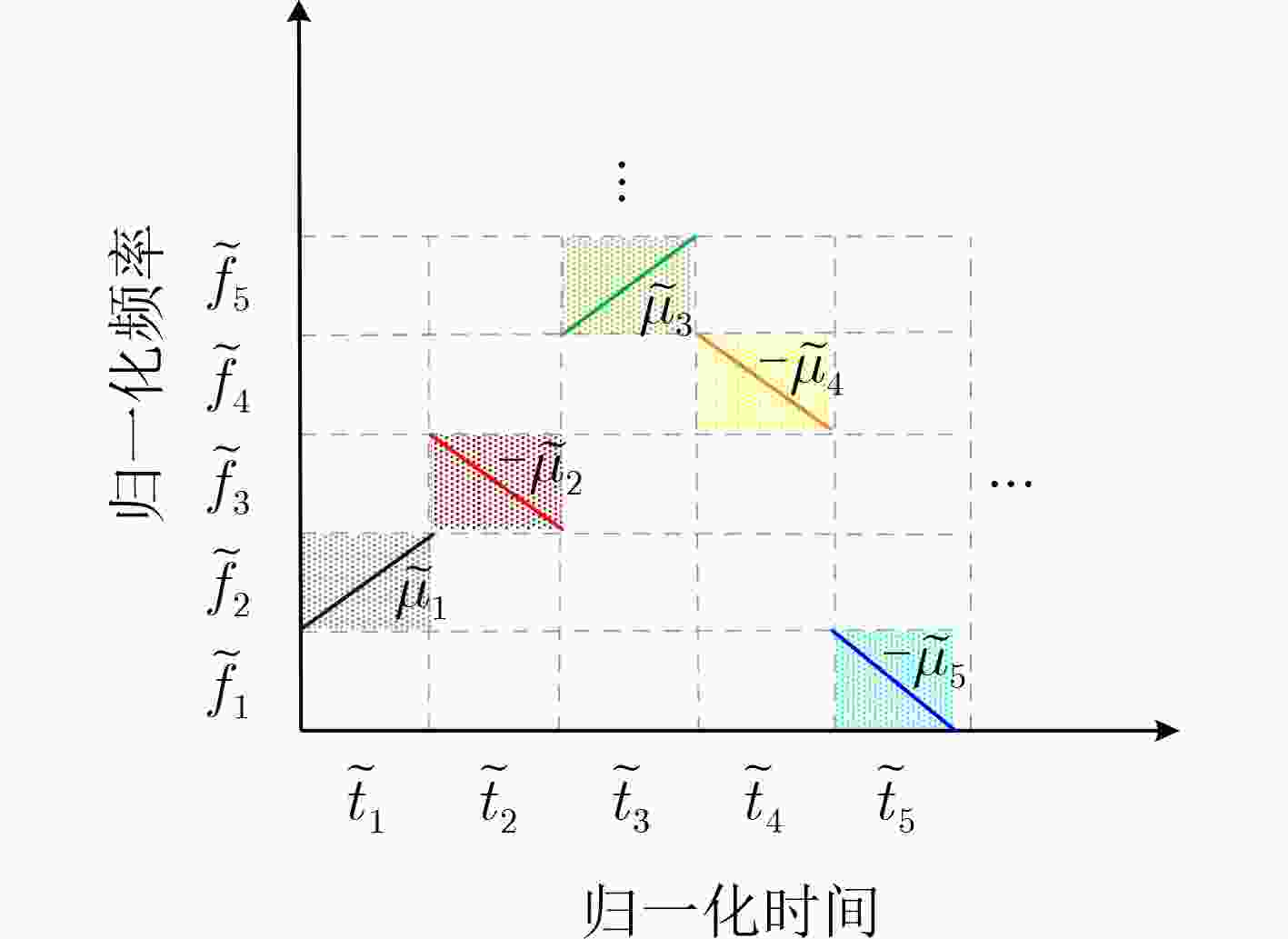
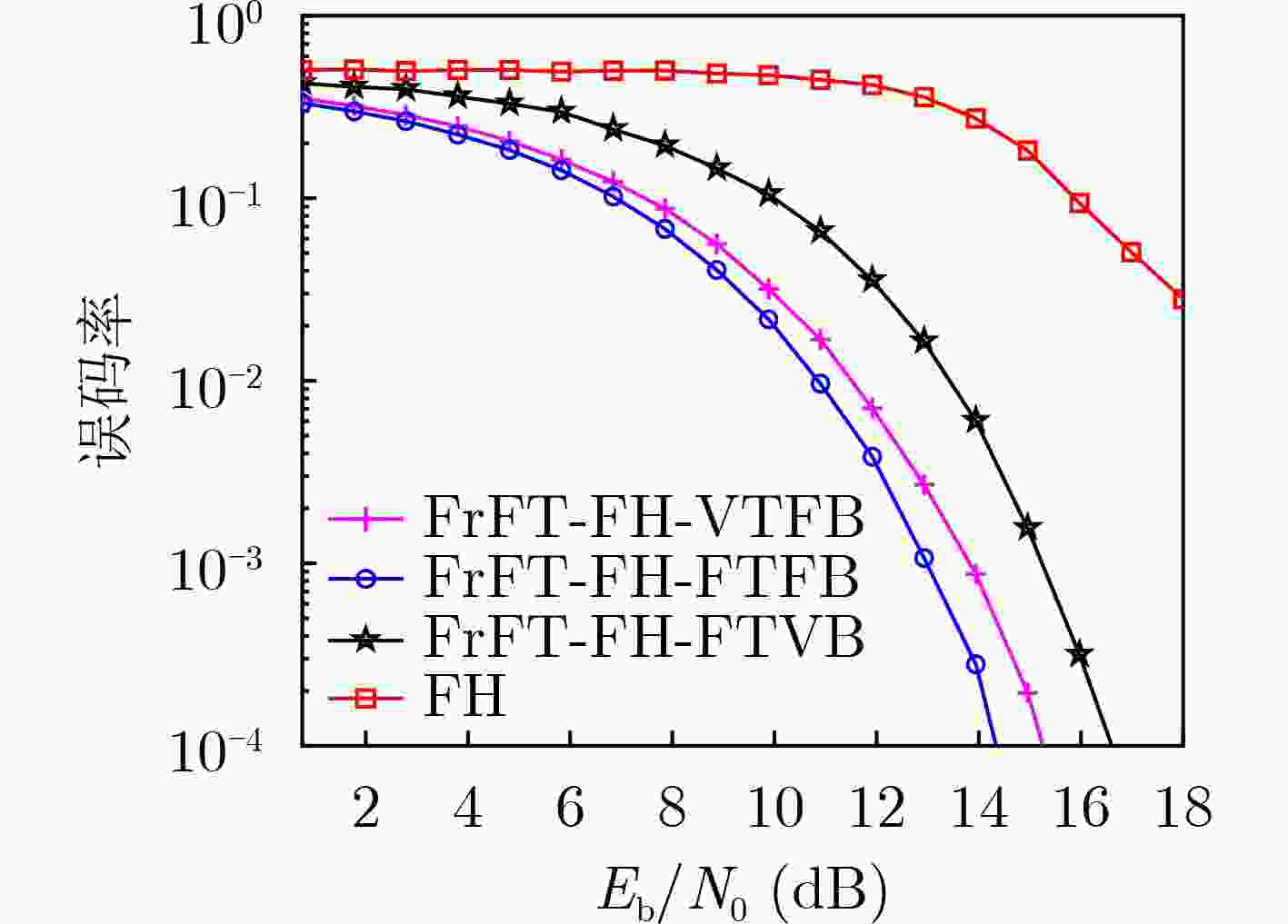
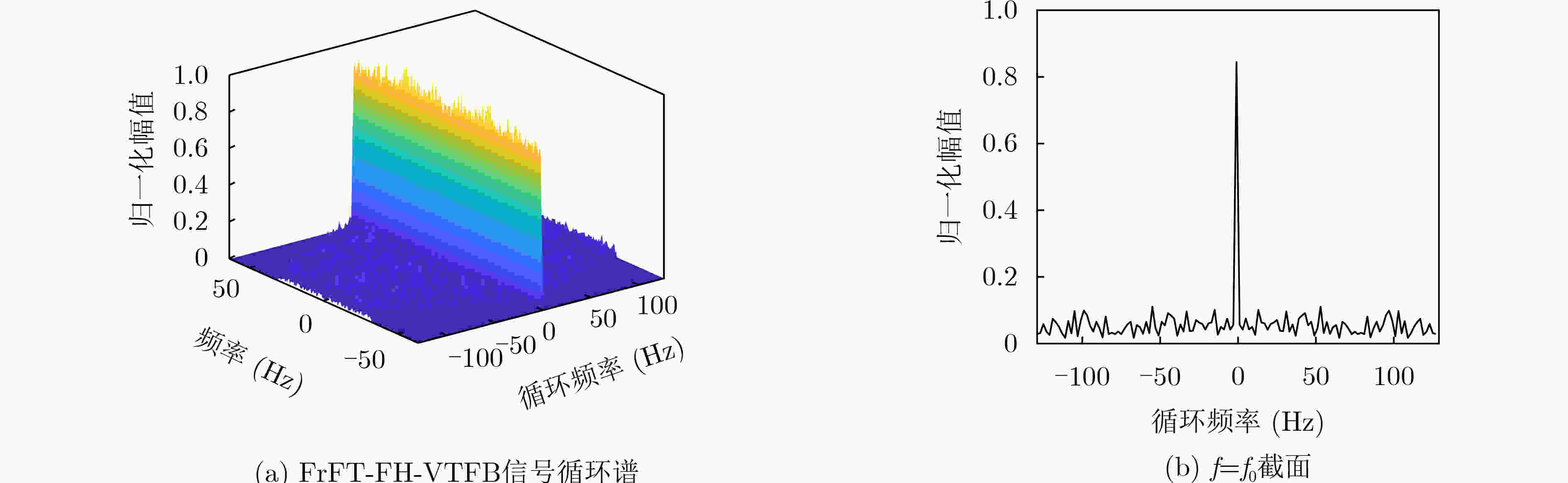
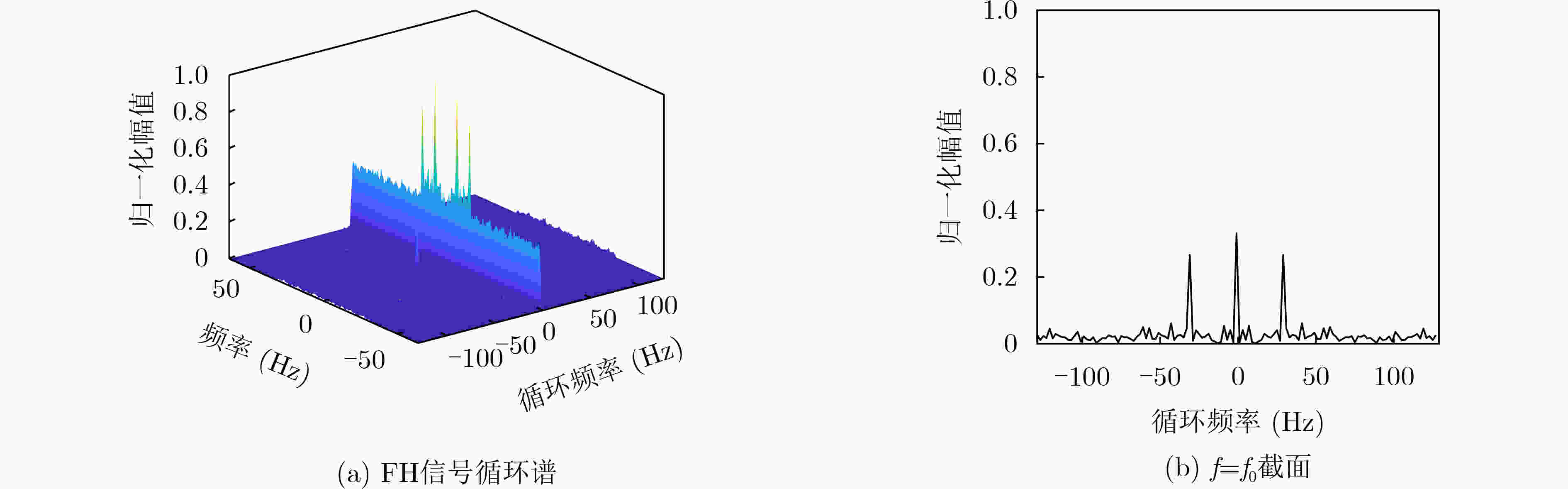
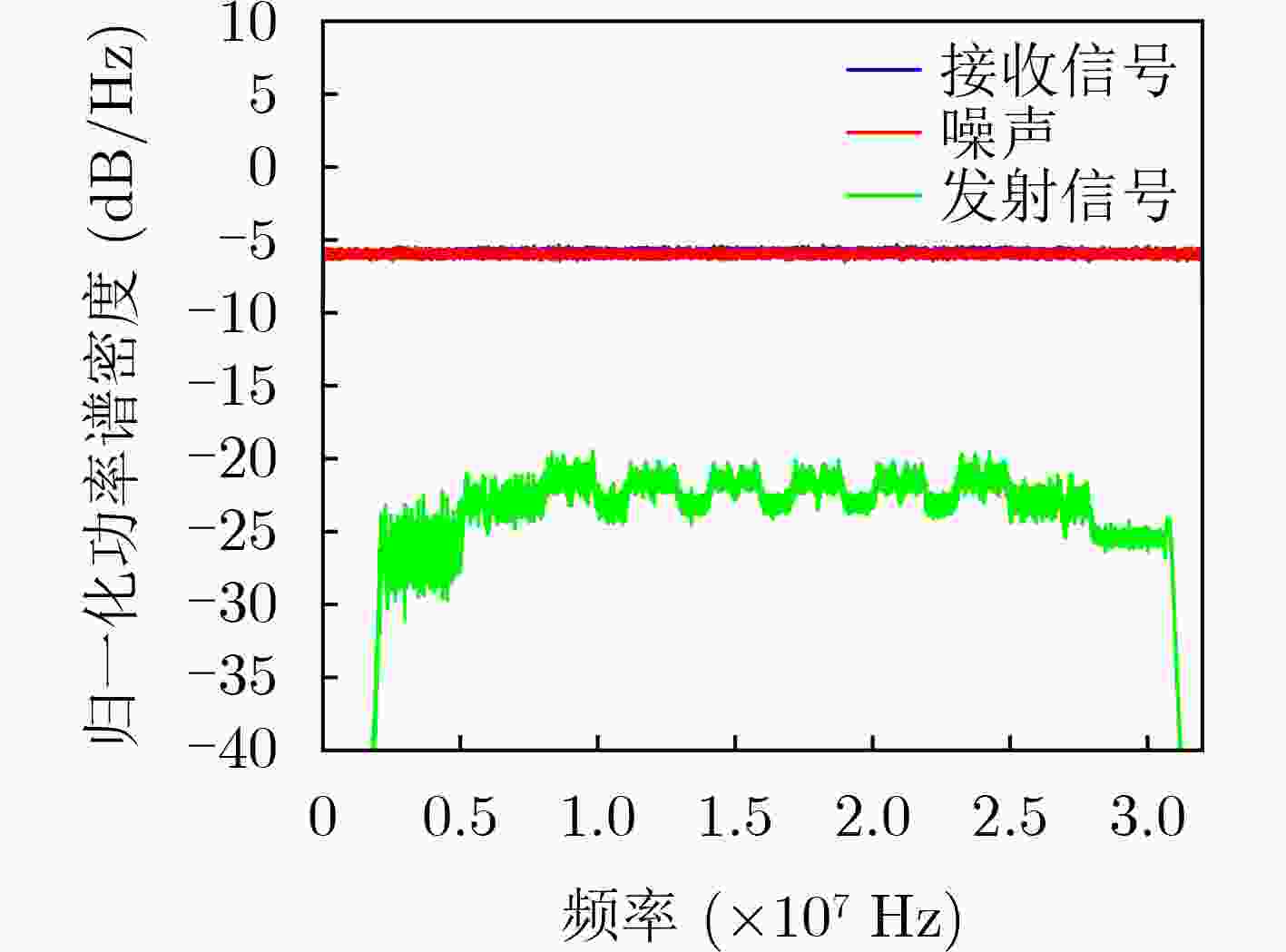
摘要: 传统跳频(FH)通信技术具有抗干扰能力强、截获概率低等优点,广泛应用在军民领域。针对检测传统跳频的手段越来越成熟,信息易被截获的问题,该文借鉴正交频分复用(OFDM)系统框架,提出一种基于离散分数阶傅里叶变换(DFrFT)的时宽与起始频率跳变的分数阶跳频(FrFT-FH-VTFB)系统,设计了一种新的系统框架,实现信息隐蔽传输的同时,通过DFrFT的工程实现规避传统跳频工程应用中跳速受频率合成器限制的问题。该系统通过两组不同伪随机序列选取时宽与起始频率跳变的Chirp基信号,实现系统参数的多维变换,打破系统的周期特性。此外,建立了系统发送与接收两端数学模型,并在此基础上推导了系统在白噪声信道下的理论误码率。仿真结果表明,该文所设计的系统有较好的抗衰落性能;且功率谱淹没在噪声之下,时频域特征无明显周期特性,有较好的隐蔽性。Abstract: Because of the advantages of strong anti-interference ability and low probability of interception, Frequency Hopping (FH) is widely used in military and civilian fields. In view of the increasingly mature means of detecting FH and the information is easy to be intercepted, by drawing on the Orthogonal Frequency Division Multiplexing (OFDM) system framework, a Fractional Fourier Transform Frequency Hopping with Variable Time Wide and Fixed Bandwidth (FrFT-FH-VTFB) system based on Discrete Fractional Fourier Transform (DFrFT) is proposed in this paper and a new system framework is designed. While realizing the covert transmission of information, the DFrFT is used to avoid the problem that the hopping speed is limited by the frequency synthesizer. The system uses two PN sequences to select Chirp signals with different time width and frequency to achieve multi-dimensional transformation of system parameters. In addition, this paper establishes the relevant mathematical model and derives the theoretical bit error rate of the system under white noise channel. The simulation results show that the system designed in this paper has better anti-fading performance, the power spectrum is submerged under noise and the time-frequency domain characteristics have no obvious periodic characteristics.
-
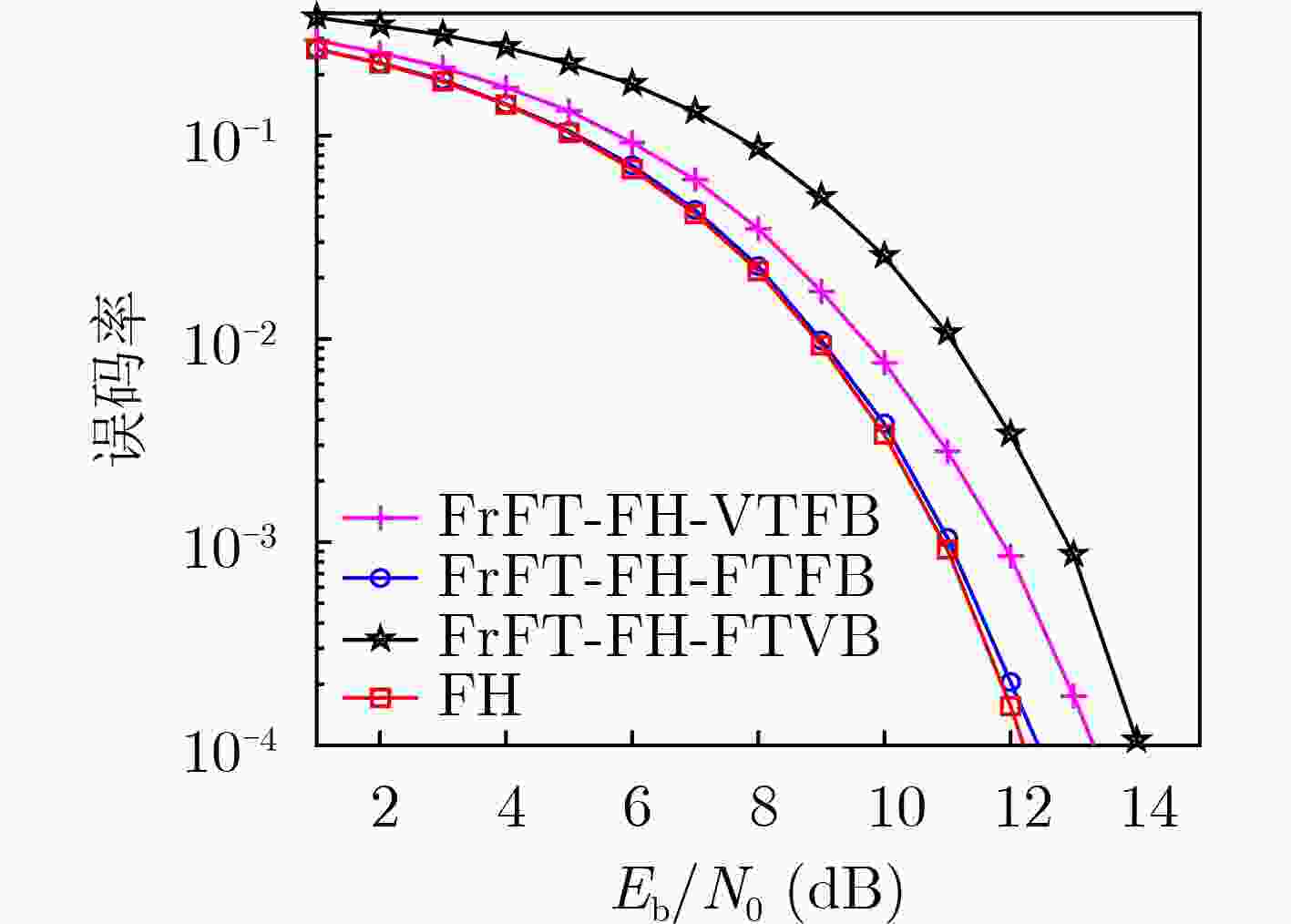
表 1 各系统参数设置
系统 基信号 跳点 时宽个数 带宽个数 平均时宽带宽积 平均带宽(MHz) 平均时宽(μs) FrFT-FH-VTFB Chirp 16 8 1 250 20 12.5 FrFT-FH-FTFB Chirp 16 1 1 250 20 12.5 FrFT-FH-FTVB Chirp 16 1 8 250 20 12.5 FH 正弦信号 16 1 1 – 20 12.5 -
[1] ZENG Xiangyong, CAI Han, TANG Xiaohu, et al. A class of optimal frequency hopping sequences with new parameters[J]. IEEE Transactions on Information Theory, 2012, 58(7): 4899–4907. doi: 10.1109/tit.2012.2195771 [2] QUAN Houde, ZHAO Huan, and CUI Peizhang. Anti-jamming frequency hopping system using multiple hopping patterns[J]. Wireless Personal Communications, 2015, 81(3): 1159–1176. doi: 10.1007/s11277-014-2177-1 [3] JUNG J and LIM J. Chaotic standard map based frequency hopping OFDMA for low probability of intercept[J]. IEEE Communications Letters, 2011, 15(9): 1019–1021. doi: 10.1109/LCOMM.2011.071811.110966 [4] 陈智, 李少谦, 董彬虹. 差分跳频通信系统抗部分频带噪声干扰的性能分析[J]. 电子与信息学报, 2007, 29(6): 1324–1327.CHEN Zhi, LI Shaoqian, and DONG Binhong. Performance analysis of differential frequency hopping system under partial band noise jamming[J]. Journal of Electronics &Information Technology, 2007, 29(6): 1324–1327. [5] LING Qi and LI Tongtong. Message-driven frequency hopping: Design and analysis[J]. IEEE Transactions on Wireless Communications, 2009, 8(4): 1773–1782. doi: 10.1109/TWC.2009.071255 [6] LI Yang, YAO Fuqiang, and XU Ba. High order differential frequency hopping: Design and analysis[J]. Mathematical Problems in Engineering, 2015, 2015: 586080. doi: 10.1155/2015/586080 [7] SHA Zhichao, LIU Zhangmeng, HUANG Zhitao, et al. Online hop timing detection and frequency estimation of multiple FH signals[J]. ETRI Journal, 2013, 35(5): 748–756. doi: 10.4218/etrij.13.0112.0787 [8] LEE K G and OH S J. Detection of fast frequency-hopping signals using dirty template in the frequency domain[J]. IEEE Wireless Communications Letters, 2019, 8(1): 281–284. doi: 10.1109/LWC.2018.2870275 [9] HU Chenlin, KIM J Y, NA S Y, et al. Compressive frequency hopping signal detection using spectral kurtosis and residual signals[J]. Wireless Personal Communications, 2017, 94(1): 53–67. doi: 10.1007/s11277-015-3156-x [10] NING Ben, GUAN Lei, and HUANG Haiyan. A novel frequency-hopping sequence for covert communication[J]. IEEE Access, 2017, 5: 20157–20163. doi: 10.1109/ACCESS.2017.2756100 [11] LEE K G and OH S J. Detection of frequency-hopping signals with deep learning[J]. IEEE Communications Letters, 2020, 24(5): 1042–1046. doi: 10.1109/LCOMM.2020.2971216 [12] 杨宇晓, 汪德鑫, 黄琪. 四维超混沌射频隐身跳频通信设计方法[J]. 宇航学报, 2020, 41(10): 1341–1349. doi: 10.3873/j.issn.1000-1328.2020.10.012YANG Yuxiao, WANG Dexin, and HUANG Qi. Design method of radio frequency stealth frequency hopping communications based on four-dimensional hyperchaotic system[J]. Journal of Astronautics, 2020, 41(10): 1341–1349. doi: 10.3873/j.issn.1000-1328.2020.10.012 [13] TU Xingbin, XU Xiaomei, ZOU Zheguang, et al. Fractional Fourier domain hopped communication method based on chirp modulation for underwater acoustic channels[J]. Journal of Systems Engineering and Electronics, 2017, 28(3): 449–456. doi: 10.21629/JSEE.2017.03.05 [14] 宁晓燕, 梁洪广, 王震铎, 等. 二维随机跳频系统性能分析[J]. 哈尔滨工程大学学报, 2022, 43(2): 274–281. doi: 10.11990/jheu.202012012NING Xiaoyan, LIANG Hongguang, WANG Zhenduo, et al. Performance analysis of a two-dimensional random frequency hopping system[J]. Journal of Harbin Engineering University, 2022, 43(2): 274–281. doi: 10.11990/jheu.202012012 [15] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360–364. doi: 10.3969/j.issn.1001-0645.2005.04.019ZHAO Xinghao, DENG Bing, and TAO Ran. Dimensional normalization in the digital computation of the fractional fourier transform[J]. Transactions of Beijing Institute of Technology, 2005, 25(4): 360–364. doi: 10.3969/j.issn.1001-0645.2005.04.019 [16] 史军, 沙学军, 张钦宇. 分数阶信号处理理论与方法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2017: 77–82.SHI Jun, SHA Xuejun, and ZHANG Qinyu. Fractional Order Signal Processing Theory and Methods[M]. Harbin: Harbin Institute of Technology Press, 2017: 77–82. [17] 刘建成, 刘忠, 王雪松, 等. 高斯白噪声背景下的LFM信号的分数阶Fourier域信噪比分析[J]. 电子与信息学报, 2007, 29(10): 2337–2340. doi: 10.3724/SP.J.1146.2006.00314LIU Jiancheng, LIU Zhong, WANG Xuesong, et al. SNR analysis of LFM signal with gaussian white noise in fractional fourier transform domain[J]. Journal of Electronics &Information Technology, 2007, 29(10): 2337–2340. doi: 10.3724/SP.J.1146.2006.00314 [18] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 349–350.TAO Ran, DENG Bing, and WANG Yue. Fractional Fourier Transform and its Applications[M]. Beijing: Tsinghua University Press, 2009: 349–350. [19] 樊昌信, 曹丽娜. 通信原理[M]. 7版. 北京: 国防工业出版社, 2012: 189–195.FAN Changxin and CAO Lina. Principles of Communications[M]. 7th ed. Beijing: National Defense Industry Press, 2012: 189–195. [20] 崔伟亮, 江桦, 李剑强, 等. 改进的循环谱估计快速算法与性能分析[J]. 电子与信息学报, 2011, 33(7): 1594–1599. doi: 10.3724/SP.J.1146.2010.01170CUI Weiliang, JIANG Hua, LI Jianqiang, et al. Improved fast cyclic spectral estimation algorithm and performance analysis[J]. Journal of Electronics &Information Technology, 2011, 33(7): 1594–1599. doi: 10.3724/SP.J.1146.2010.01170 [21] ZHANG Wei, MALLIK R K, and LETAIEF K B. Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2009, 8(12): 5761–5766. doi: 10.1109/TWC.2009.12.081710 [22] 齐佩汉, 司江勃, 李赞, 等. 基于功率谱分段对消频谱感知算法研究及性能分析[J]. 电子与信息学报, 2014, 36(4): 769–774. doi: 10.3724/SP.J.1146.2013.01091QI Peihan, SI Jiangbo, LI Zan, et al. Research and performance analysis of spectrum sensing algorithm based on the power spectral density segment cancellation[J]. Journal of Electronics &Information Technology, 2014, 36(4): 769–774. doi: 10.3724/SP.J.1146.2013.01091 -





 下载:
下载:



 下载:
下载:
