内孤立波环境下稳健降阶自适应匹配场定位方法研究

李杰美慧; 史阳; 杨益新; 黄晓冬

doi:10.11999/JEIT211333

内孤立波环境下稳健降阶自适应匹配场定位方法研究

doi: 10.11999/JEIT211333

李杰美慧^{1, 2},
史阳^{1, 2, ,},
杨益新^{1, 2},
黄晓冬³

1.
西北工业大学航海学院西安 710000
2.
陕西省水下信息技术重点实验室西安 710000
3.
中国海洋大学物理海洋教育部重点实验室青岛 266000

基金项目: 国家自然科学基金(41906160, 11974286, 12174312)

详细信息

作者简介:
李杰美慧：女，1994年生，博士生，研究方向为内波环境下稳健的阵列信号处理

史阳：男，1986年生，副教授，研究方向为水声信息处理、动态海洋声学

杨益新：男，1975年生，教授，研究方向为水声阵列信号处理及其应用

黄晓冬：男，1987年生，副教授，研究方向为内波观测、理论分析与预测保障

通讯作者:
史阳　shiyang@nwpu.edu.cn

中图分类号: TN929.3; TB566
计量
- 文章访问数: 683
- HTML全文浏览量: 356
- PDF下载量: 89
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-25
- 修回日期: 2022-05-19
- 网络出版日期: 2022-05-24
- 刊出日期: 2022-06-21

Robust Adaptive Matched Field Processing of Rank Reduction for Source Localization under Internal Solitary Waves

LI Jiemeihui^{1, 2},
SHI Yang^{1, 2
, ,},
YANG Yixin^{1, 2},
HUANG Xiaodong³

1.
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710000, China
2.
Shaanxi Key Laboratory of Underwater Information Technology, Xi’an 710000, China
3.
Physical Oceanography Laboratory, Ocean University of China, Qingdao 266000, China

Funds: The National Natural Science Foundation of China (41906160, 11974286, 12174312)

摘要

摘要: 海洋内孤立波的存在会引起海水混合，温盐结构改变，从而导致声速在时间和空间上的不均匀分布，而在匹配场定位中则表现为声速失配，定位不准确。该文提出一种内孤立波下稳健的降阶自适应匹配场定位方法(RR-AMFP)。在传统自适应匹配场定位算法的基础上，融合了主分量抑制波束形成方法，通过特征分解对拷贝协方差矩阵进行降阶，抑制噪声空间，同时采用抑制系数和权重因子来计算匹配过程中的权向量，监测失配的拷贝向量。因此该算法可以在内孤立波环境下保持更好的稳健性，而且阶数的降低也缩短了计算时间。仿真结果表明：该算法可以实现单个内孤立波下的准确定位，但大振幅的内孤立波波列仍然会造成较大的定位误差。在南海开展了内孤立波环境下的声源定位实验，估计距离误差为3.7%，深度误差为1.6%，验证了该算法在实际海洋内孤立波环境下的有效性。
- 水下声源定位 /
- 自适应匹配场定位 /
- 内孤立波 /
- 降阶 /
- 南海
Abstract: The mismatch of sound speed induced by internal solitary waves will cause the inaccurate estimation in the matched field processing for source localization. In this paper, a robust Adaptive Matched Field Processing method of Rank Reduction (RR-AMFP) for internal solitary waves is proposed. Based on the traditional adaptive matched field processing algorithm, this method integrates dominant mode rejection beamforming, and reduces the rank of sampling covariance matrix by eigen-decomposition, and suppresses the noise space. Meanwhile, a suppressing coefficient and a weighting factor are used to calculate the weight vector in the matching process, and the mismatched coping vectors are detected. Therefore, this method can maintain better robustness in the internal solitary wave environment, and the reduction of rank also shortens the calculation time. The simulation results show that this method can accurately estimate the source location under a single internal solitary wave, but the internal solitary wave train with large amplitude will still lead to more errors of estimation. The estimated distance error is 3.3% and depth error is 1.5% in the localization experiment of internal solitary waves in the South China Sea, which belongs to reliable localization. The experiment results demonstrate the effectiveness of the method in the actual environment with internal solitary waves.
- Underwater source localization /
- Adaptive matched field processing /
- Internal solitary wave /
- Rank reduction /
- South China Sea

HTML全文

图 1 无内孤立波和有内孤立波时的声速场(南海实测数据)

下载: 全尺寸图片幻灯片

图 2 算法整体框图

下载: 全尺寸图片幻灯片

图 3 实验整体布置

下载: 全尺寸图片幻灯片

图 4 3种处理器的模糊表面(无内孤立波)

下载: 全尺寸图片幻灯片

图 5 3种处理器的模糊表面(有内孤立波)

下载: 全尺寸图片幻灯片

图 6 不同振幅单个内孤立波和波列的声速场

下载: 全尺寸图片幻灯片

图 7 不同振幅单个内孤立波和波列下RR-AMFP定位模糊表面

下载: 全尺寸图片幻灯片

图 8 实验中水听器接收信号(深度为125 m)

下载: 全尺寸图片幻灯片

图 9 3种处理器实验定位模糊表面

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	BAGGEROER A B, KUPERMAN W A, and MIKHALEVSKY P N. An overview of matched field methods in ocean acoustics[J]. IEEE Journal of Oceanic Engineering, 1993, 18(4): 401–424. doi: 10.1109/48.262292
[2]	BUCKER H P. Use of calculated sound fields and matched-field detection to locate sound sources in shallow water[J]. The Journal of the Acoustical Society of America, 1976, 59(2): 368–373. doi: 10.1121/1.380872
[3]	BAGGEROER A B, KUPERMAN W A, and SCHMIDT H. Matched field processing: Source localization in correlated noise as an optimum parameter estimation problem[J]. The Journal of the Acoustical Society of America, 1988, 83(2): 571–587. doi: 10.1121/1.396151
[4]	李焜, 方世良, 安良. 非合作水声脉冲信号的单水听器匹配场定位研究[J]. 电子与信息学报, 2012, 34(11): 2541–2547. doi: 10.3724/SP.J.1146.2012.00547 LI Kun, FANG Shiliang, and AN Liang. Matched field localization for non-cooperative underwater acoustic pulse signals using a single hydrophone[J]. Journal of Electronics &Information Technology, 2012, 34(11): 2541–2547. doi: 10.3724/SP.J.1146.2012.00547
[5]	ZHU Guolei, WANG Yingmin, and WANG Qi. Matched field processing based on Bayesian estimation[J]. Sensors, 2020, 20(5): 1374. doi: 10.3390/s20051374
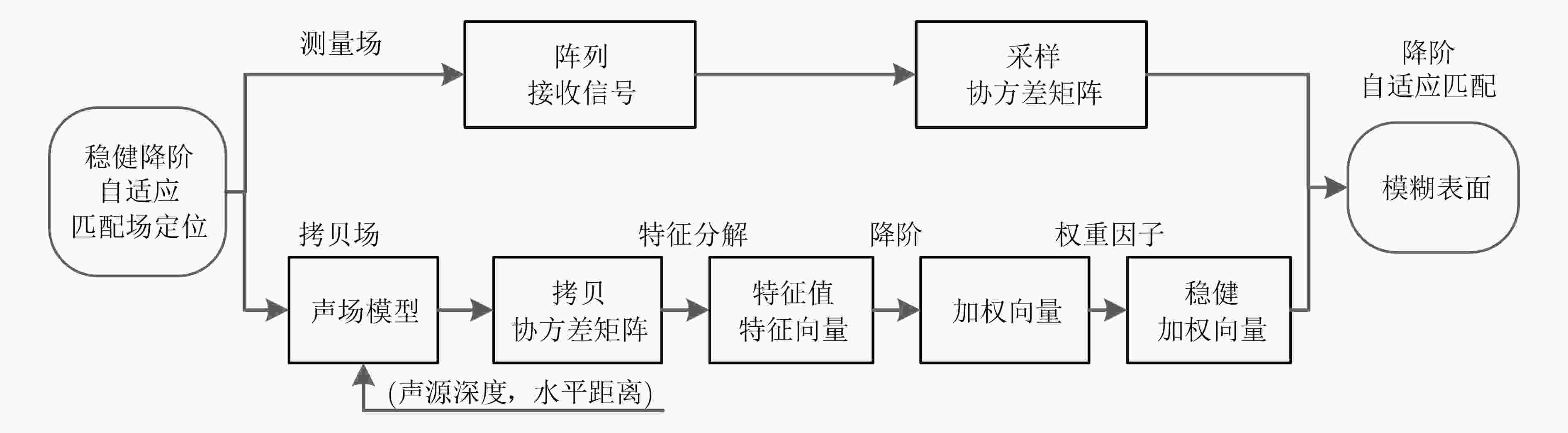
[6]	魏尚飞, 韩东, 张海勇, 等. 基于矩阵特征分解的水下声源匹配场定位[J]. 舰船科学技术, 2021, 43(19): 141–148. doi: 10.3404/j.issn.1672-7649.2021.10.029 WEI Shangfei, HAN Dong, ZHANG Haiyong, et al. Underwater sound source location with matched field processing based on matrix Eigen decomposition[J]. Ship Science and Technology, 2021, 43(19): 141–148. doi: 10.3404/j.issn.1672-7649.2021.10.029
[7]	杨坤德, 段睿, 李辉, 等. 水下声源定位理论与技术[M]. 北京: 电子工业出版社, 2019: 65–144. YANG Kunde, DUAN Rui, LI Hui, et al. Theory and Technology of Underwater Source Localization[M]. Beijing: Electronics Industry Press, 2019: 65–144.
[8]	SHMELEV A, LIN Y T, and LYNCH J. Low-frequency acoustic propagation through crossing internal waves in shallow water[J]. Journal of Theoretical and Computational Acoustics, 2020, 28(3): 1950013. doi: 10.1142/S2591728519500130
[9]	杨坤德. 水声信号的匹配场处理技术研究[D]. [博士论文], 西北工业大学, 2003. YANG Kunde. A study on matched field processing of underwater acoustic signals[D]. [Ph. D. dissertation], Northwestern Polytechnical University, 2003.
[10]	APEL J R, OSTROVSKY L A, STEPANYANTS Y A, et al. Internal solitons in the ocean and their effect on underwater sound[J]. The Journal of the Acoustical Society of America, 2007, 121(2): 695–722. doi: 10.1121/1.2395914
[11]	李整林, 杨益新, 秦继兴, 等. 深海声学与探测技术[M]. 上海: 上海科学技术出版社, 2020: 15–37. LI Zhenglin, YANG Yixin, QIN Jixing, et al. Acoustics and Detection Technology in the Deep Sea[M]. Shanghai: Shanghai Science and Technology Press, 2020: 15–37.
[12]	马树青. 浅海孤立子内波对声传播的影响[D]. [博士论文], 哈尔滨工程大学, 2011. MA Shuqing. Influence of shallow water internal solitary waves on sound propagation[D]. [Ph. D. dissertation], Harbin Engineering University, 2011.
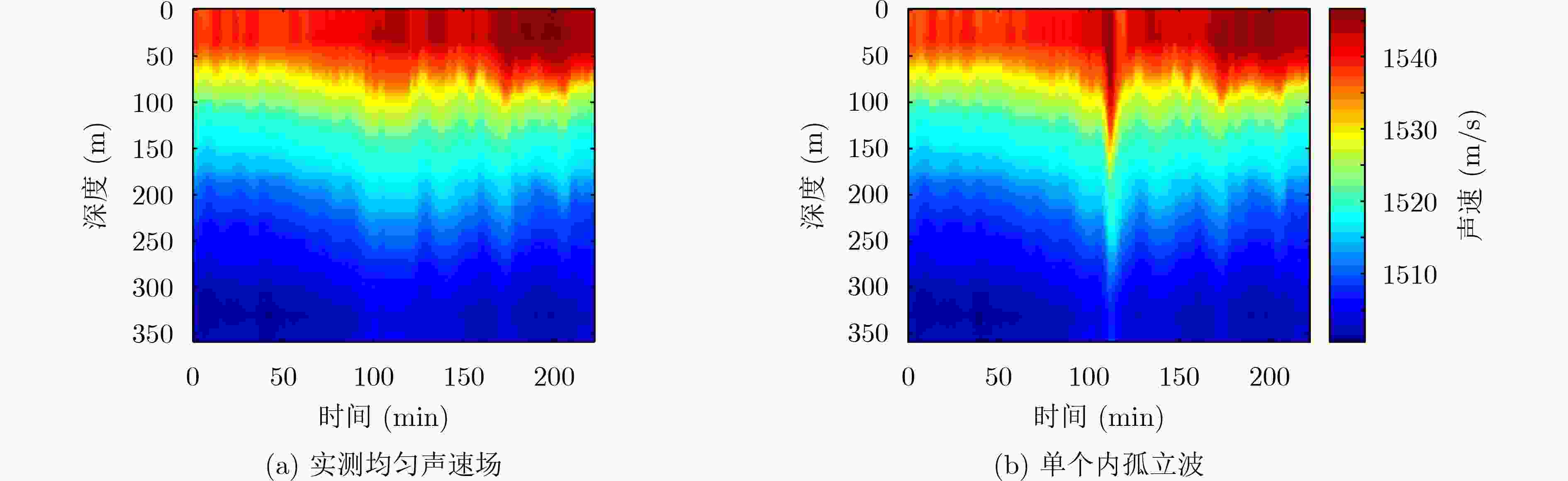
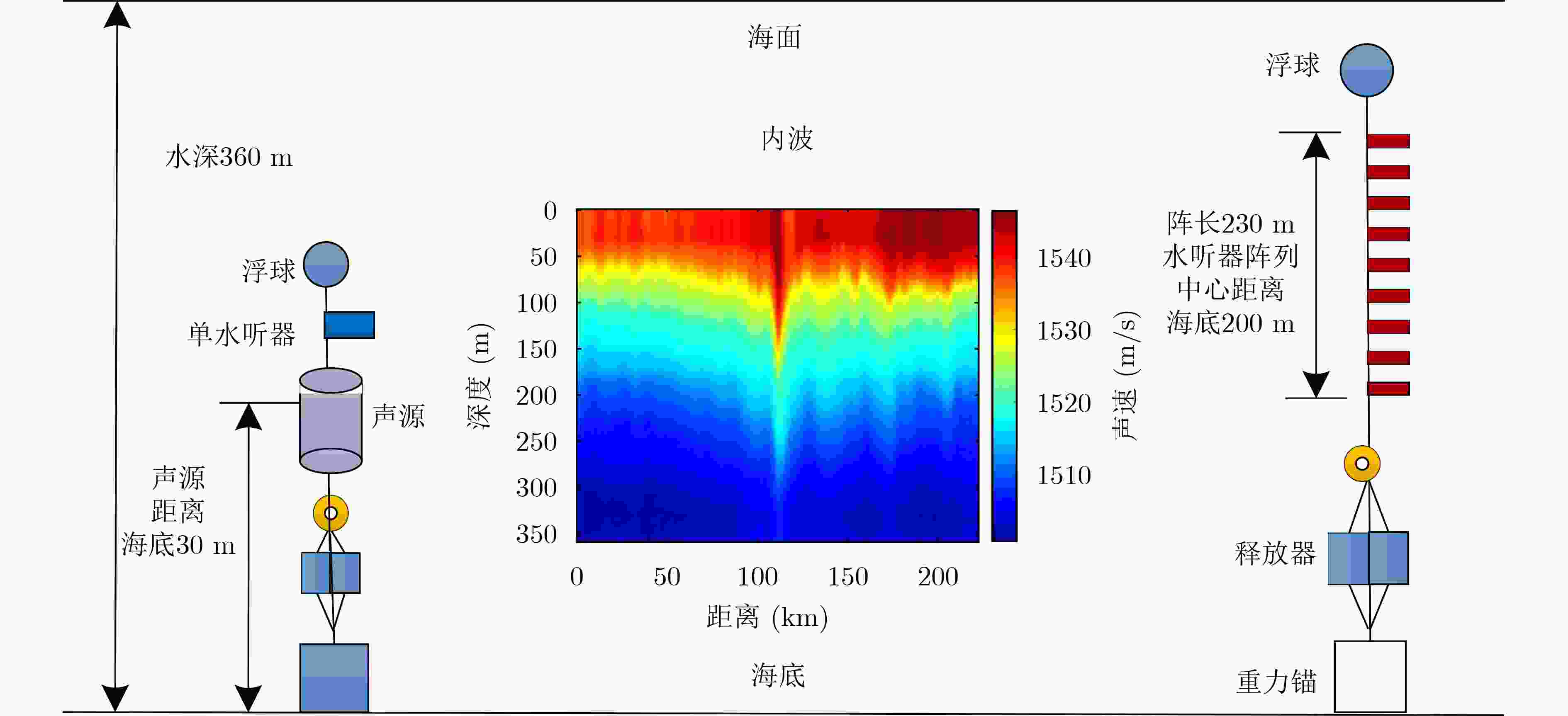
[13]	祝捍皓, 肖瑞, 朱军, 等. 三维浅海环境下孤立子内波对低频声能流的传播影响[J]. 声学学报, 2021, 46(3): 365–374. doi: 10.15949/j.cnki.0371-0025.2021.03.005 ZHU Hanhao, XIAO Rui, ZHU Jun, et al. Influence of internal solitary waves on sound propagation in three-dimensional shallow sea[J]. Acta Acustica, 2021, 46(3): 365–374. doi: 10.15949/j.cnki.0371-0025.2021.03.005
[14]	DAUGHERTY J R and LYNCH J F. Surface wave, internal wave, and source motion effects on matched field processing in a shallow water waveguide[J]. The Journal of the Acoustical Society of America, 1990, 87(6): 2503–2526. doi: 10.1121/1.399098
[15]	李整林. 浅海中内波、波浪起伏和海底粗糙对匹配场定位的影响[D]. [博士论文], 中国科学院声学研究所, 2002. LI Zhenglin. The effects of internal waves, surface fluctuation and bottom roughness on matched field source localization in shallow water[D]. [Ph. D. dissertation], The Institute of Acoustics of the Chinese Academy of Sciences, 2002.
[16]	吴开明. 南中国海北部内波环境下匹配场定位研究[D]. [博士论文], 中国科学院研究生院, 2009. WU Kaiming. Matched field position study in the internal wave environment in the north of South China Sea[D]. [Ph. D. dissertation], The Institute of Acoustics of the Chinese Academy of Sciences, 2009.
[17]	李永飞, 赵航芳. 内波环境下的时频匹配场定位方法[J]. 哈尔滨工程大学学报, 2020, 41(10): 1605–1610. doi: 10.11990/jheu.202007081 LI Yongfei and ZHAO Hangfang. A time-frequency matched field location method in the presence of internal waves[J]. Journal of Harbin Engineering University, 2020, 41(10): 1605–1610. doi: 10.11990/jheu.202007081
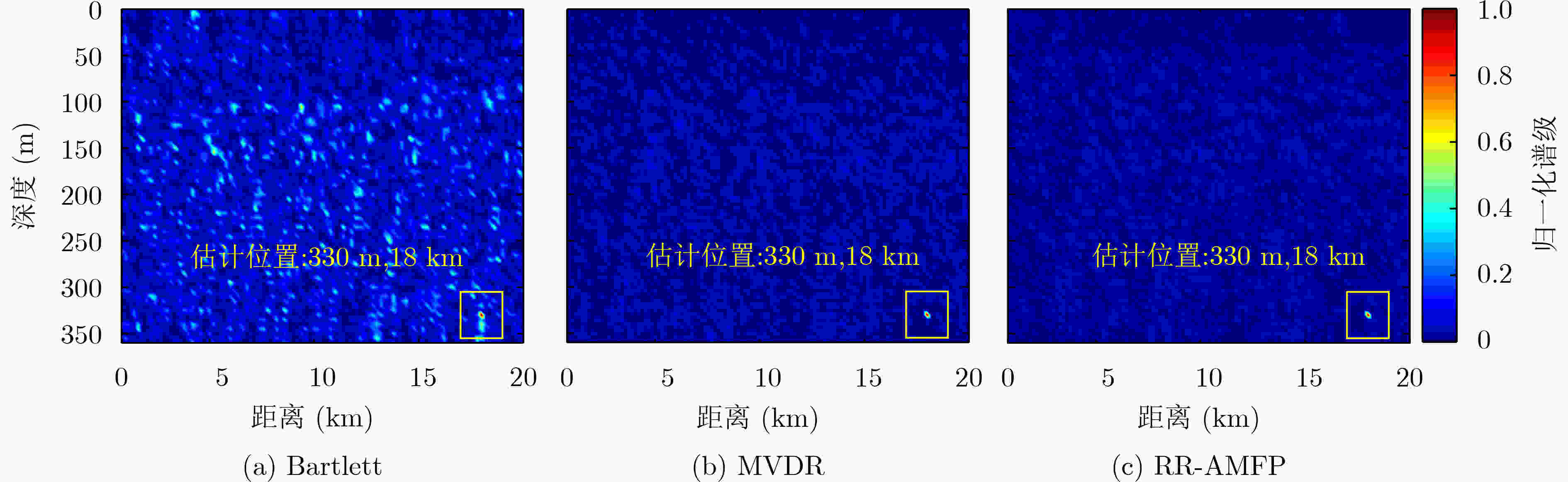
[18]	ABRAHAM D A and OWSLEY N L. Beamforming with dominant mode rejection[C]. Conference Proceedings on Engineering in the Ocean Environment, Washington, USA, 1990: 470–475.