Circuit Model Analysis of General Charge-controlled Memristor Based on Hyperbolic Functions
-
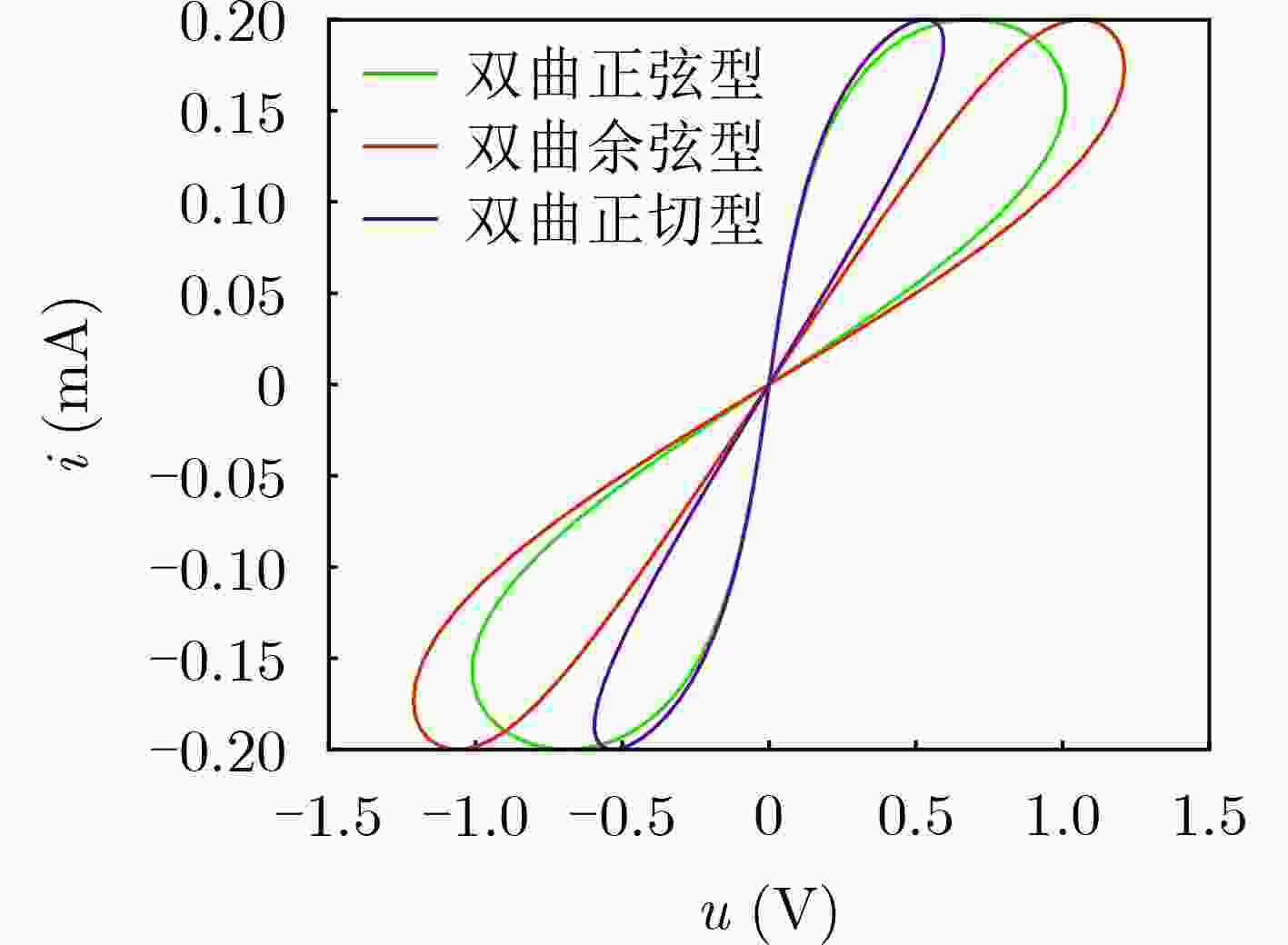
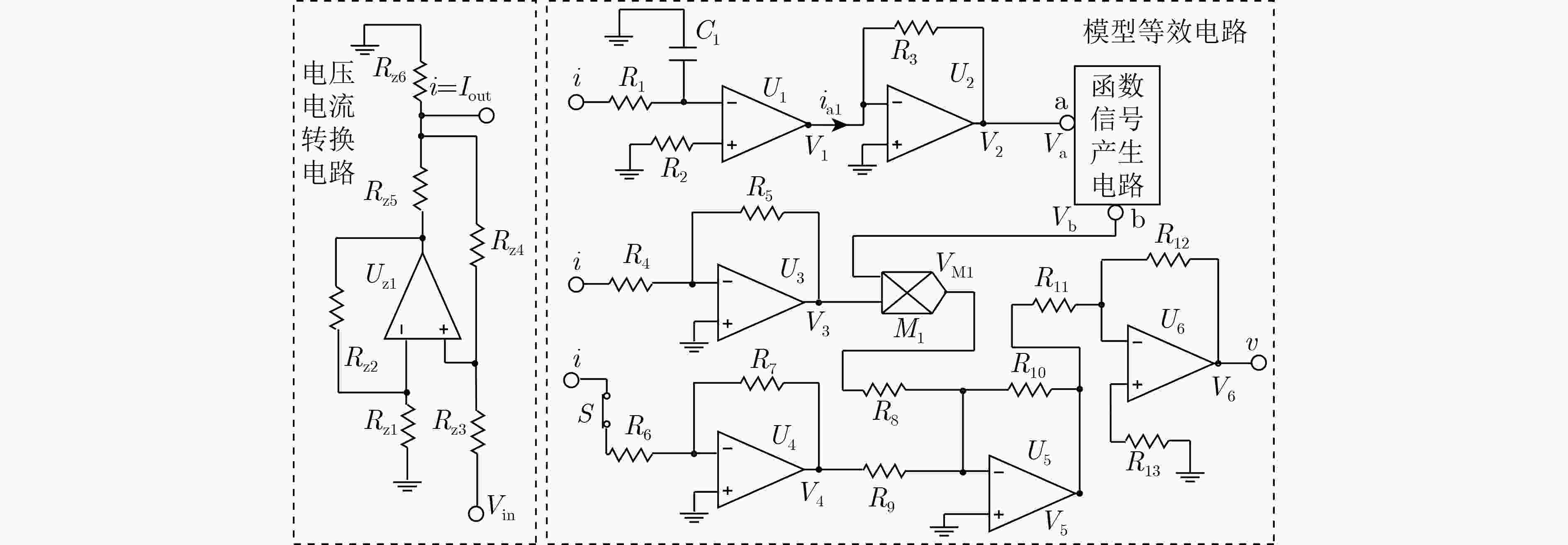
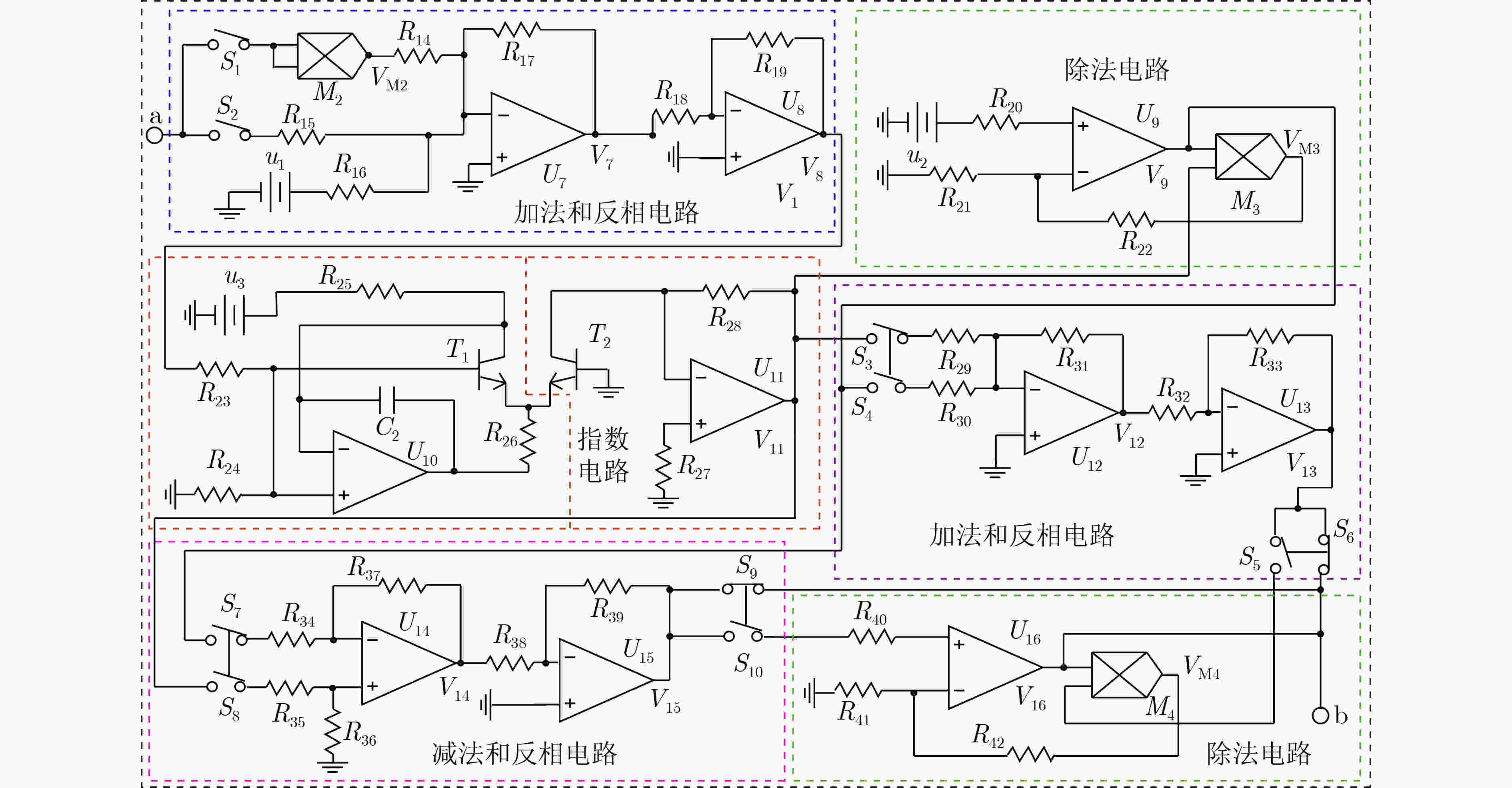
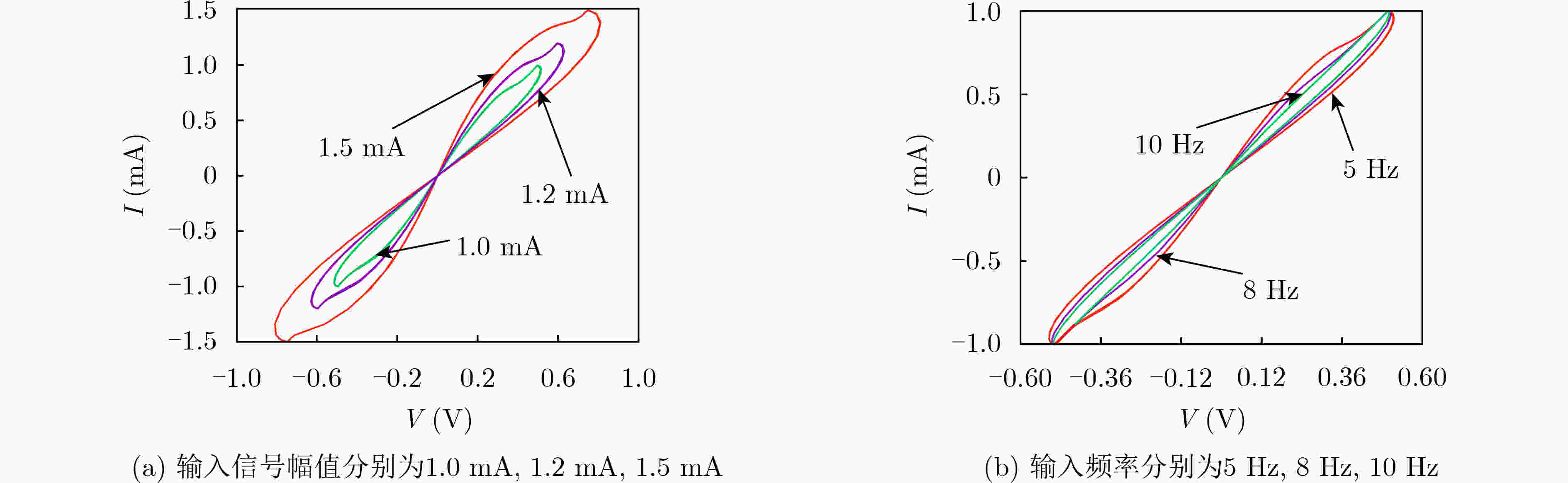
摘要: 目前,忆阻器模拟器的研究主要集中在磁控忆阻器,对荷控忆阻器模拟器的研究不多,双曲函数型的荷控忆阻器模拟器也很少涉及。因此,该文提出一种基于双曲函数的通用型荷控忆阻器模拟器。模拟器通过电压-电流的相互转换电路,实现电路中电压和电流信号之间的相互转换,再通过电路中对应的电路模块对产生的信号进行计算,最终得到通用型双曲荷控忆阻器模型。模拟器能够实现双曲正弦、双曲余弦以及双曲正切函数对应的荷控忆阻器模型。通用型双曲函数荷控忆阻器模拟器对应的等效电路,主要由运算放大器、电阻、电容、三极管等基本元件组成。分析模拟器在不同幅值以及不同频率的输入信号下的伏安特性曲线,得出荷控忆阻器模拟器符合记忆元件的基本特性。该文提出的通用型双曲函数荷控忆阻器模型,对忆阻器模型的发展具有一定的参考意义。Abstract: At present, most of the researches on the memristor simulators are flux-controlled, there are few researches on the charge-controlled memristor simulator, and the hyperbolic function simulator is seldom mentioned. Therefore, a general-purpose simulator of charge-controlled memristor based on hyperbolic function is proposed. The simulator realizes the conversion between voltage and current signals in the circuit through the voltage-current mutual conversion circuit, and calculates the generated signals through the corresponding module in the circuit, and finally obtains the universal hyperbolic charge-controlled memristor model. The simulator can realize the charge-controlled memristor corresponding to hyperbolic sine, hyperbolic cosine and hyperbolic tangent function. The equivalent circuit of the general-purpose hyperbolic function charge-controlled memristor simulator is mainly composed of operational amplifier, resistor, capacitor, triode and other basic components. By analyzing the volt-ampere characteristic curves of the simulator at different amplitudes and different frequencies, it is concluded that the simulator conforms to the basic characteristics of memory devices. The model of hyperbolic charge-controlled memristor presented in this paper has a certain reference significance for the development of memristor model.
-
表 1 双曲正弦荷控忆阻器数学模型和电路模型
开关
状态u1状态 忆阻数学模型 忆阻器电路模型 S1断开
S2闭合u1$ \ne $0 $M(q) = a \cdot \sinh (b + cq) + {{p} }$ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ {l{R_{39} } } }{ { {R_{38} } } }{R_5} \cdot \sinh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{16} } } }{u_1} \right.\\ \left. + \frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{15} } } }\rho q\right] + \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_9} } }{R_7} \\ \end{gathered}$ S1闭合
S2闭合u1$ = $0 $M(q) = a \cdot \sinh (cq + d{q^2}) + {{p} }$ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ {l{R_{39} } } }{ { {R_{38} } } }{R_5} \cdot \sinh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{15} } } }\rho q \right. \\ \left. + \frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{14} } } }{\rho ^2}{q^2}\right] + \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_9} } }{R_7} \\ \end{gathered}$ S1闭合
S2断开u1$ \ne $0 $M(q) = a \cdot \sinh (b + d{q^2}) + {{p} }$ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ {l{R_{39} } } }{ { {R_{38} } } }{R_5} \cdot \sinh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{16} } } }{u_1} \right. \\ \left. + \frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{14} } } }{\rho ^2}{q^2}\right] + \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_9} } }{R_7} \\ \end{gathered}$ S1闭合
S2闭合u1$ \ne $0 $\begin{gathered} M(q) = a \cdot \sinh (b + cq + d{q^2}) \\ {\text{ } } + {{p} } \\ \end{gathered}$ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ {l{R_{39} } } }{ { {R_{38} } } }{R_5} \cdot \sinh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{16} } } }{u_1} \right. \\ \left.\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{15} } } }\rho q{\text{ + } }\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{14} } } }{\rho ^2}{q^2}\right] + \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_9} } }{R_7} \\ \end{gathered}$ 表 2 双曲余弦荷控忆阻器数学模型和电路模型
开关
状态u1状态 忆阻数学模型 忆阻器电路模型 S1断开
S2闭合u1$ \ne $0 $M(q) = a'' \cdot \cosh (b'' + c''q) + {{p} }''$ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{g{R_{33}}}}{{{R_{32}}}}{R_5} \cdot \cosh \left[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{16}}}}{u_1} \right.\\ \left. + \frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{15}}}}\rho q \right.] + \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_9}}}{R_7} \\ \end{gathered} $ S1闭合
S2闭合u1$ = $0 $\begin{gathered} M(q) = a'' \cdot \cosh (c''q + d''{q^2}) + \\ {{ p} }'' \\ \end{gathered}$ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{{\text{g}}{R_{33}}}}{{{R_{32}}}}{R_5} \cdot \cosh \left.[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{15}}}}\rho q \right. \\ \left. + \frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{14}}}}{\rho ^2}{q^2}\right] + \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_9}}}{R_7} \\ \end{gathered} $ S1闭合
S2断开u1$ \ne $0 $M(q) = a'' \cdot \cosh (b'' + d''{q^2}) + {{p} }''$ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ { {\text{g} }{R_{33} } } }{ { {R_{32} } } }{R_5} \cdot \cosh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{16} } } }{u_1} \right. \\ \left. + \frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{14} } } }{\rho ^2}{q^2}\right] + \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_9} } }{R_7} \\ \end{gathered}$ S1闭合
S2闭合u1$ \ne $0 $\begin{gathered} M(q) = a'' \cdot \cosh (b'' + c''q + \\ {\text{ } }d''{q^2}) + {{p} }'' \\ \end{gathered}$ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{{\text{g}}{R_{33}}}}{{{R_{32}}}}{R_5} \cdot \cosh \left[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{16}}}}{u_1} \right.\\ \left.\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{15}}}}\rho q{\text{ + }}\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{14}}}}{\rho ^2}{q^2}\right] + \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_9}}}{R_7} \\ \end{gathered} $ 表 3 双曲正切荷控忆阻器数学模型和电路模型
开关
状态u1状态 忆阻数学模型 忆阻器电路模型 S1断开
S2闭合u1$ \ne $0 $ M(q) = a''' \cdot \tanh (b''' + c'''q) $ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{l{R_{32}}{R_{39}}}}{{{\text{g}}{R_{33}}{R_{38}}}}z{R_5} \cdot \tanh \left[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{16}}}}{u_1} \right. \\ \left. + \frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{15}}}}\rho q \right] \\ \end{gathered} $ S1闭合
S2闭合u1$ = $0 $ M(q) = a''' \cdot \tanh (c'''q + d'''{q^2}) $ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{l{R_{32}}{R_{39}}}}{{{\text{g}}{R_{33}}{R_{38}}}}z{R_5} \cdot \tanh \left[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{15}}}}\rho q \right.\\ \left. + \frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{14}}}}{\rho ^2}{q^2}\right] \\ \end{gathered} $ S1闭合
S2断开u1$ \ne $0 $ M(q) = a''' \cdot \tanh (b''' + d'''{q^2}) $ $ \begin{gathered} M(q) = \frac{{{R_{12}}}}{{{R_{11}}}}\frac{{{R_{10}}}}{{{R_8}}}\frac{{l{R_{32}}{R_{39}}}}{{{\text{g}}{R_{33}}{R_{38}}}}z{R_5} \cdot \tanh \left[\frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{16}}}}{u_1} \right. \\ \left. + \frac{{{R_{24}}}}{{\left( {{R_{23}} + {R_{24}}} \right){U_T}}}\frac{{{R_{19}}}}{{{R_{18}}}}\frac{{{R_{17}}}}{{{R_{14}}}}{\rho ^2}{q^2}\right] \\ \end{gathered} $ S1闭合
S2闭合u1$ \ne $0 $ \begin{gathered} M(q) = a''' \cdot \tanh (b''' + c'''q + \\ {\text{ }}d'''{q^2}) \\ \end{gathered} $ $\begin{gathered} M(q) = \frac{ { {R_{12} } } }{ { {R_{11} } } }\frac{ { {R_{10} } } }{ { {R_8} } }\frac{ {l{R_{32} }{R_{39} } } }{ { {\text{g} }{R_{33} }{R_{38} } } }z{R_5} \cdot \tanh \left[\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{16} } } }{u_1} \right. \\ \left.\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{15} } } }\rho q{\text{ + } }\frac{ { {R_{24} } } }{ {\left( { {R_{23} } + {R_{24} } } \right){U_T} } }\frac{ { {R_{19} } } }{ { {R_{18} } } }\frac{ { {R_{17} } } }{ { {R_{14} } } }{\rho ^2}{q^2}\right] \\ \end{gathered}$ -
[1] CHUA L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. doi: 10.1109/tct.1971.1083337 [2] STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932 [3] JIANG Zizhen, WU Yi, YU Shimeng, et al. A compact model for metal-oxide resistive random access memory with experiment verification[J]. IEEE Transactions on Electron Devices, 2016, 63(5): 1884–1892. doi: 10.1109/TED.2016.2545412 [4] REUBEN J, BIGLARI M, and FEY D. Incorporating variability of resistive RAM in circuit simulations using the Stanford-PKU model[J]. IEEE Transactions on Nanotechnology, 2020, 19: 508–518. doi: 10.1109/TNANO.2020.3004666 [5] KVATINSKY S, FRIEDMAN E G, KOLODNY A, et al. TEAM: Threshold adaptive memristor model[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2013, 60(1): 211–221. doi: 10.1109/TCSI.2012.2215714 [6] YANG Zijia and WANG Xiaoping. Memristor-based BAM circuit implementation for image associative memory and filling-in[J]. Neural Computing and Applications, 2021, 33(13): 7929–7942. doi: 10.1007/s00521-020-05538-7 [7] SUN Junwei, HAN Gaoyong, ZENG Zhigang, et al. Memristor-based neural network circuit of full-function Pavlov associative memory with time delay and variable learning rate[J]. IEEE Transactions on Cybernetics, 2020, 50(7): 2935–2945. doi: 10.1109/TCYB.2019.2951520 [8] SUN Junwei, HAN Juntao, LIU Peng, et al. Memristor-based neural network circuit of Pavlov associative memory with dual mode switching[J]. AEU International Journal of Electronics and Communications, 2021, 129: 153552. doi: 10.1016/j.aeue.2020.153552 [9] ZHU Ruohua, TANG Zhiri, YE Shizhuo, et al. Memristor-based image enhancement: High efficiency and robustness[J]. IEEE Transactions on Electron Devices, 2021, 68(2): 602–609. doi: 10.1109/TED.2020.3045684 [10] CHEN Jiejie, ZENG Zhigang, and JIANG Ping. Global exponential almost periodicity of a delayed memristor-based neural networks[J]. Neural Networks, 2014, 60: 33–43. doi: 10.1016/j.neunet.2014.07.007 [11] 闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178 [12] 王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821WANG Chunhua, LIN Hairong, SUN Jingru, et al. Research progress on chaos, memory and neural network circuits based on memristor[J]. Journal of Electronics &Information Technology, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821 [13] SUN Junwei, XIAO Xiao, LIU Peng, et al. Memristive circuits design under different personality traits based on second-order damping system[J]. Microelectronics Journal, 2021, 114: 105148. doi: 10.1016/j.mejo.2021.105148 [14] WANG Zilu, HONG Qinghui, and WANG Xiaoping. Memristive circuit design of emotional generation and evolution based on skin-like sensory processor[J]. IEEE Transactions on Biomedical Circuits and Systems, 2019, 13(4): 631–644. doi: 10.1109/TBCAS.2019.2923055 [15] YU Dongsheng, ZHAO Xuanqi, SUN Tingting, et al. A simple floating mutator for emulating memristor, memcapacitor, and meminductor[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(7): 1334–1338. doi: 10.1109/TCSII.2019.2936453 [16] 洪庆辉, 曾以成, 李志军. 含磁控和荷控两种忆阻器的混沌电路设计与仿真[J]. 物理学报, 2013, 62(23): 230502. doi: 10.7498/aps.62.230502HONG Qinghui, ZENG Yicheng, and LI Zhijun. Design and simulation of chaotic circuit for flux-controlled memristor and charge-controlled memristor[J]. Acta Physica Sinica, 2013, 62(23): 230502. doi: 10.7498/aps.62.230502 [17] YANG Le, ZENG Zhigang, HUANG Yi, et al. Memristor-based circuit implementations of recognition network and recall network with forgetting stages[J]. IEEE Transactions on Cognitive and Developmental Systems, 2018, 10(4): 1133–1142. doi: 10.1109/TCDS.2018.2859303 [18] BAO Bocheng, QIAN Hui, XU Quan, et al. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based hopfield neural network[J]. Frontiers in Computational Neuroscience, 2017, 11: 81. doi: 10.3389/fncom.2017.0008 [19] 闵富红, 王珠林, 曹弋, 等. 基于双曲函数的双忆阻器混沌电路多稳态特性分析[J]. 电子学报, 2018, 46(2): 486–494. doi: 10.3969/j.issn.0372-2112.2018.02.031MIN Fuhong, WANG Zhulin, CAO Yi, et al. Multistability analysis of a dual-memristor circuit based on hyperbolic function[J]. Acta Electronica Sinica, 2018, 46(2): 486–494. doi: 10.3969/j.issn.0372-2112.2018.02.031 [20] CORINTO F and ASCOLI A. Memristive diode bridge with LCR filter[J]. Electronics Letters, 2012, 48(14): 824–825. doi: 10.1049/el.2012.1480 [21] BARBONI L. A novel passive circuit emulator for a current-controlled memristor[J]. Active and Passive Electronic Components, 2021, 2021: 5582774. doi: 10.1155/2021/5582774 -





 下载:
下载:

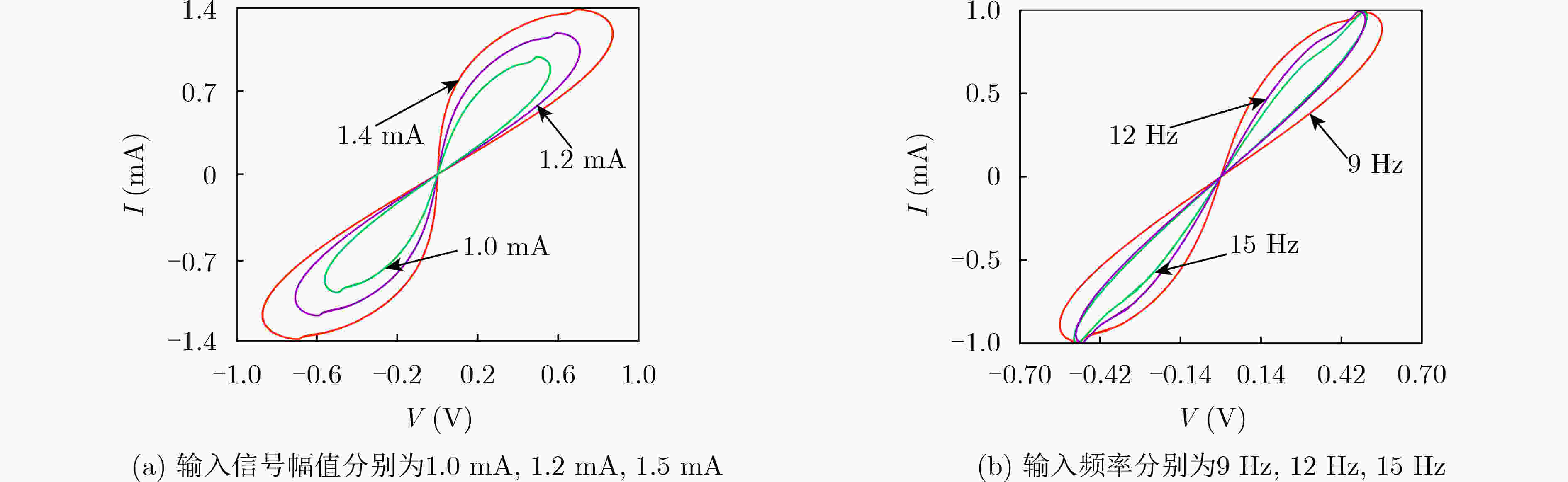
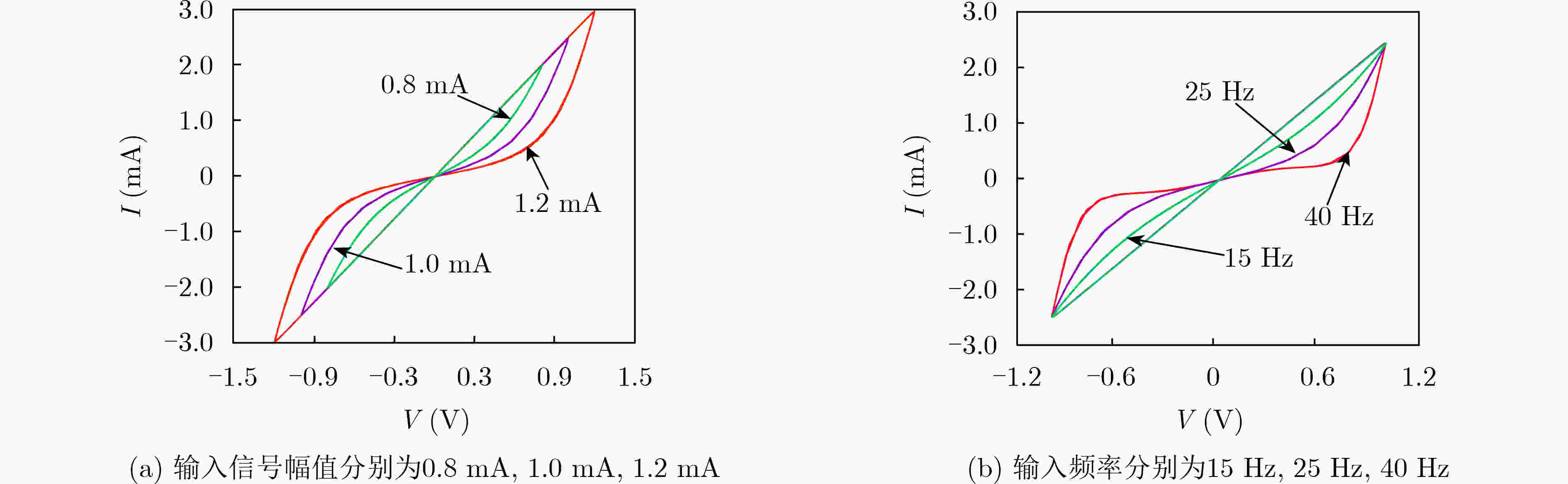


 下载:
下载:
