Combination Differential Direct Sequence Spread Spectrum Algorithm for Mobile Underwater Acoustic Communication
-
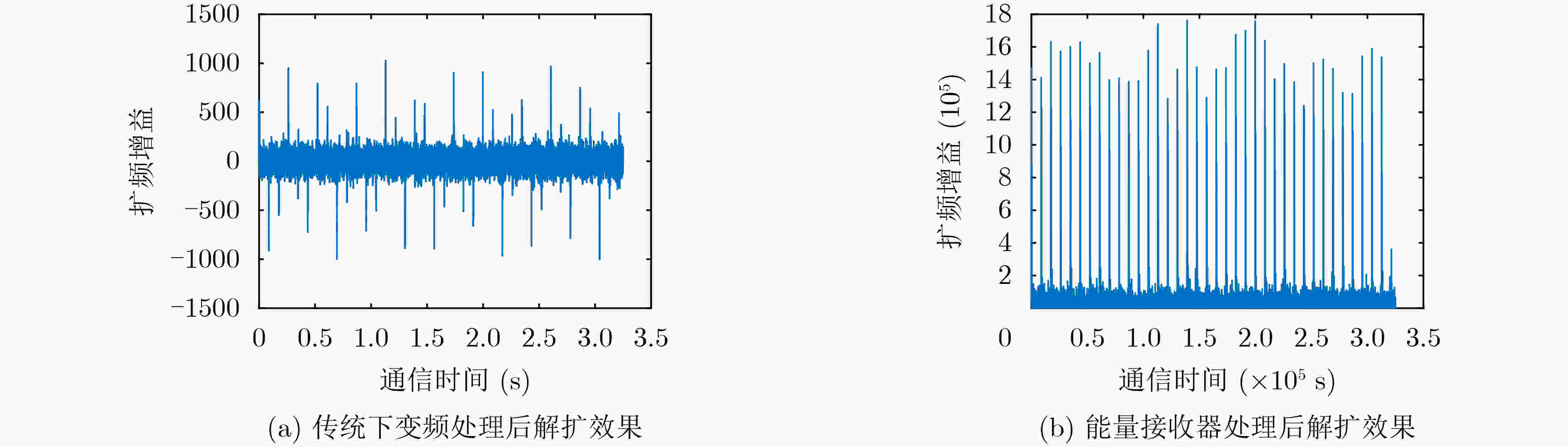
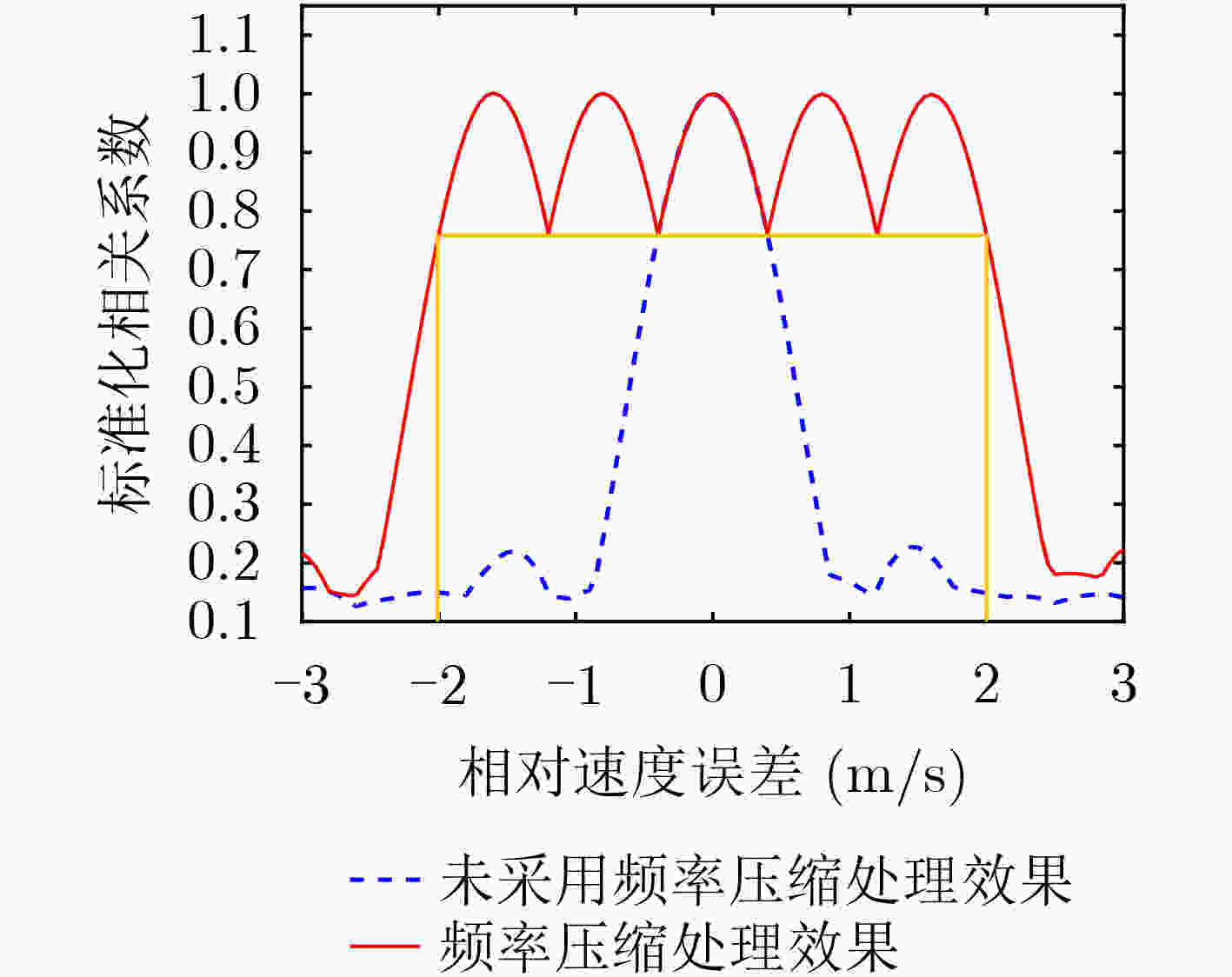
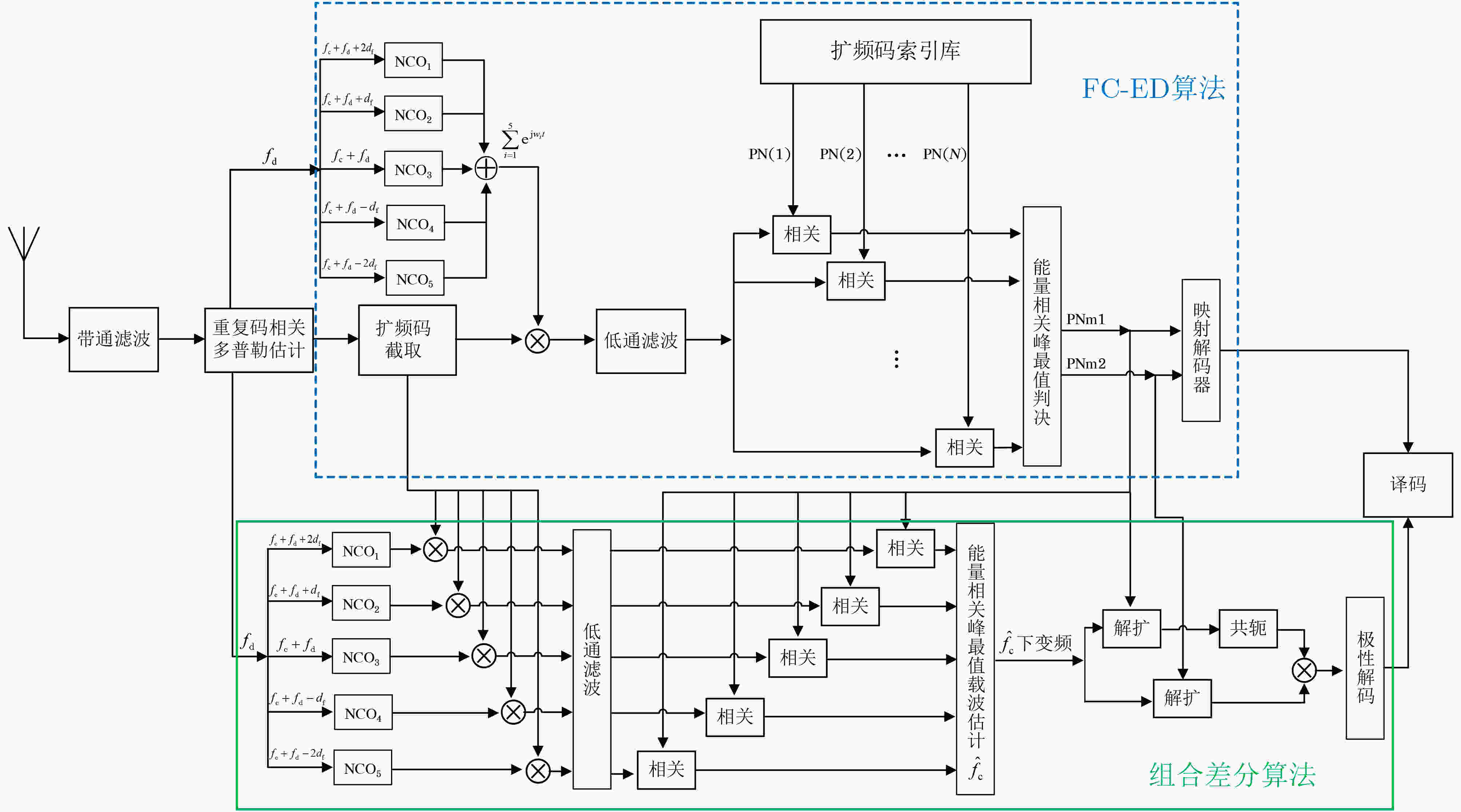
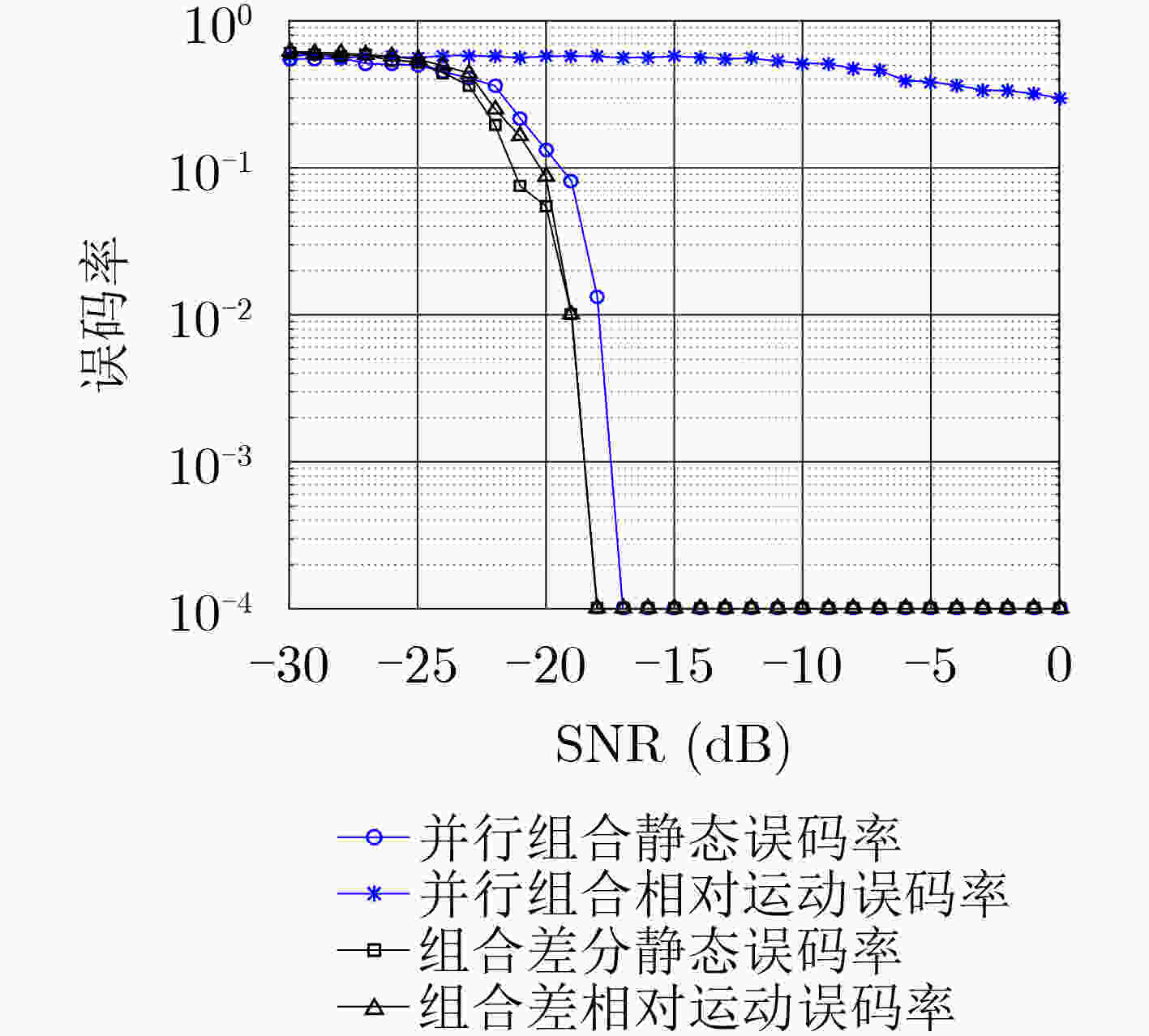
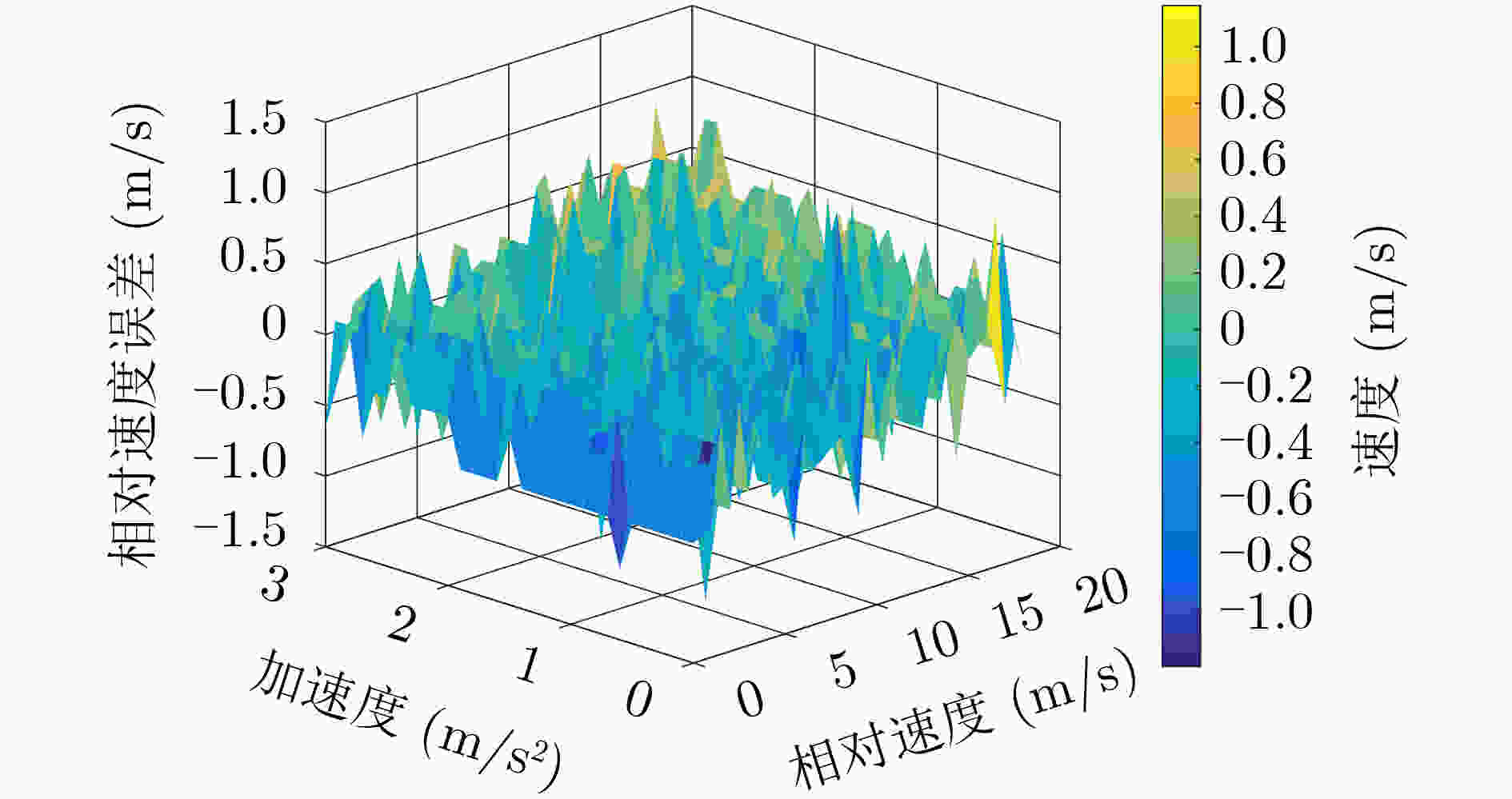
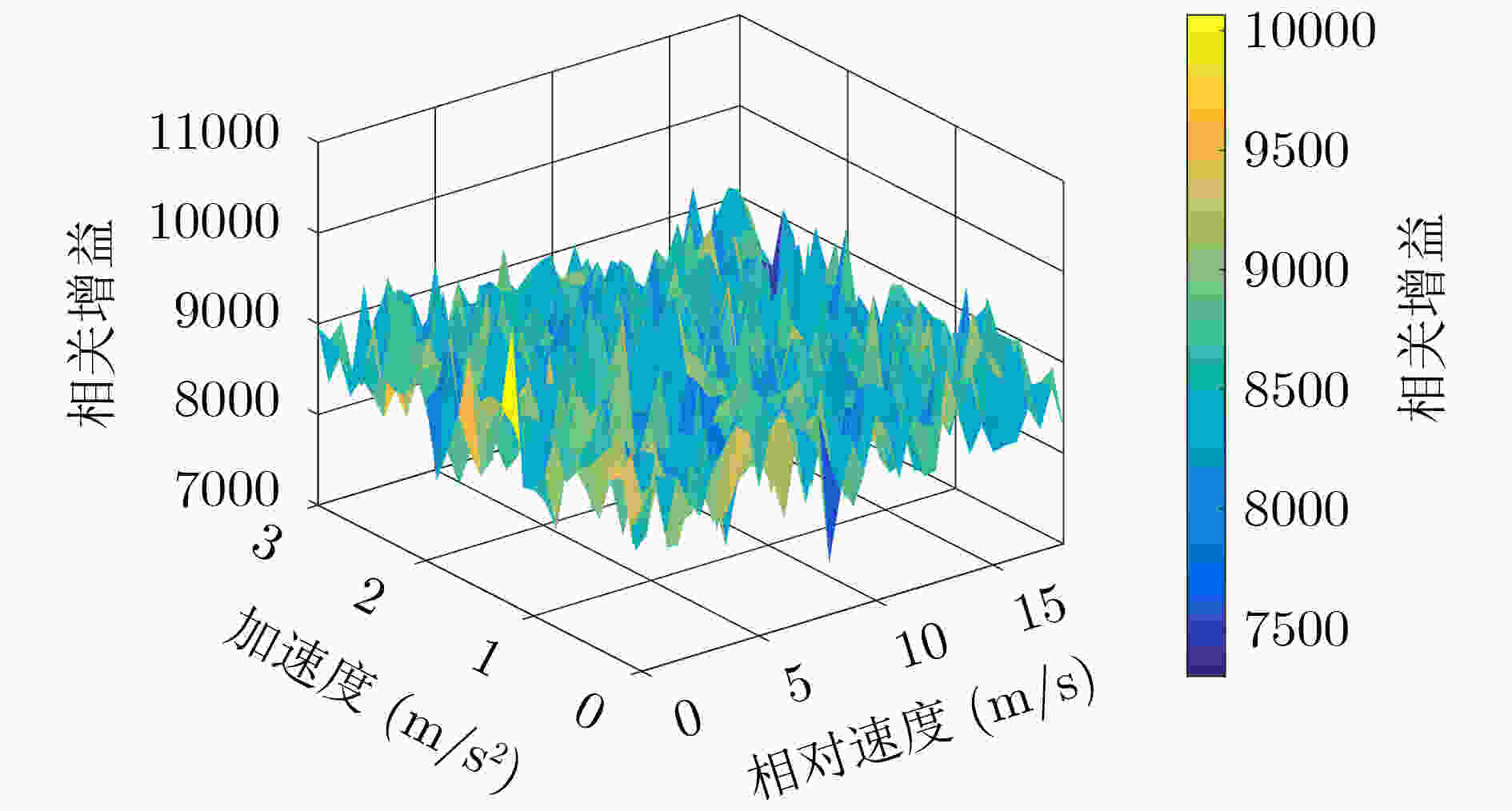
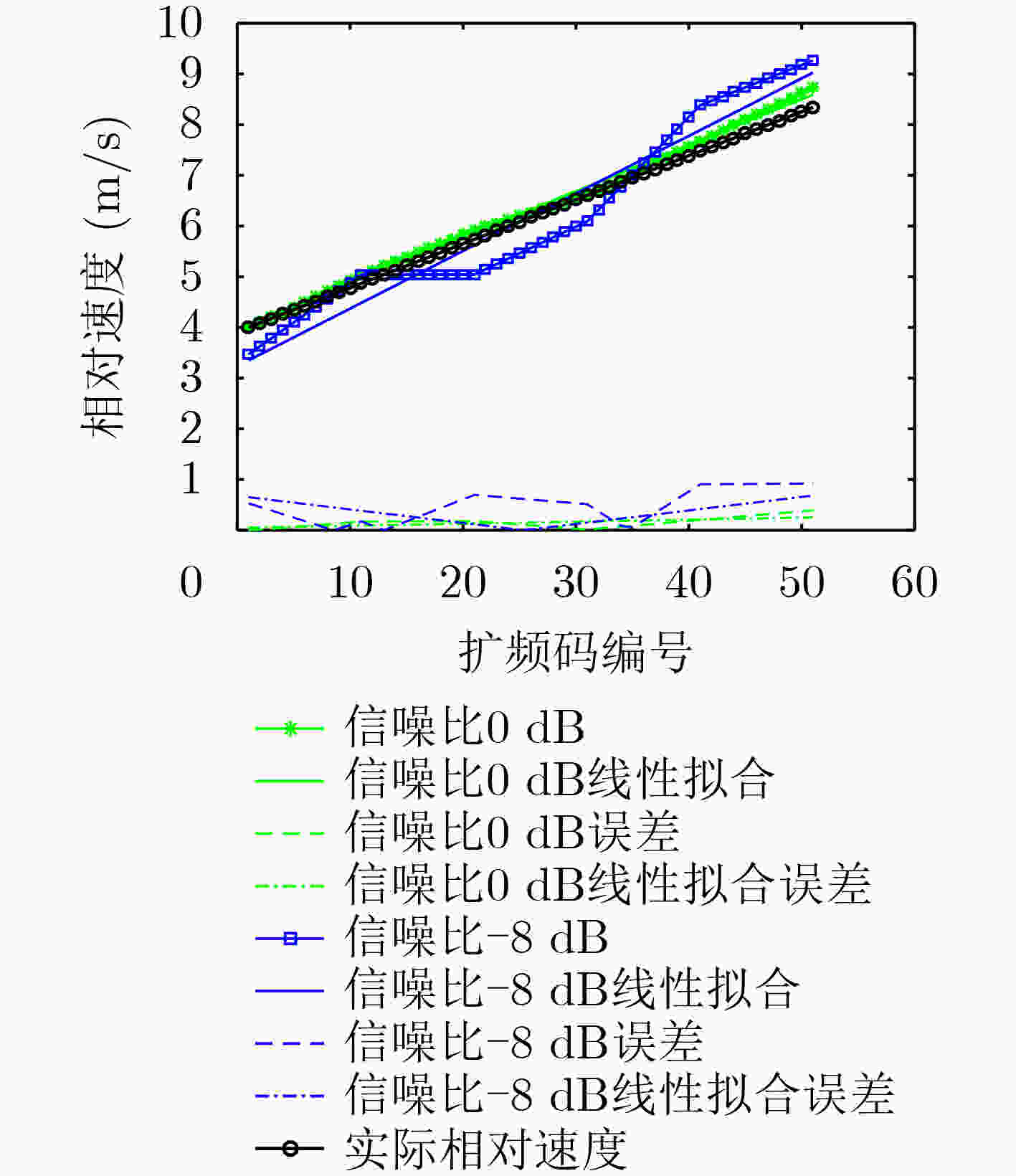
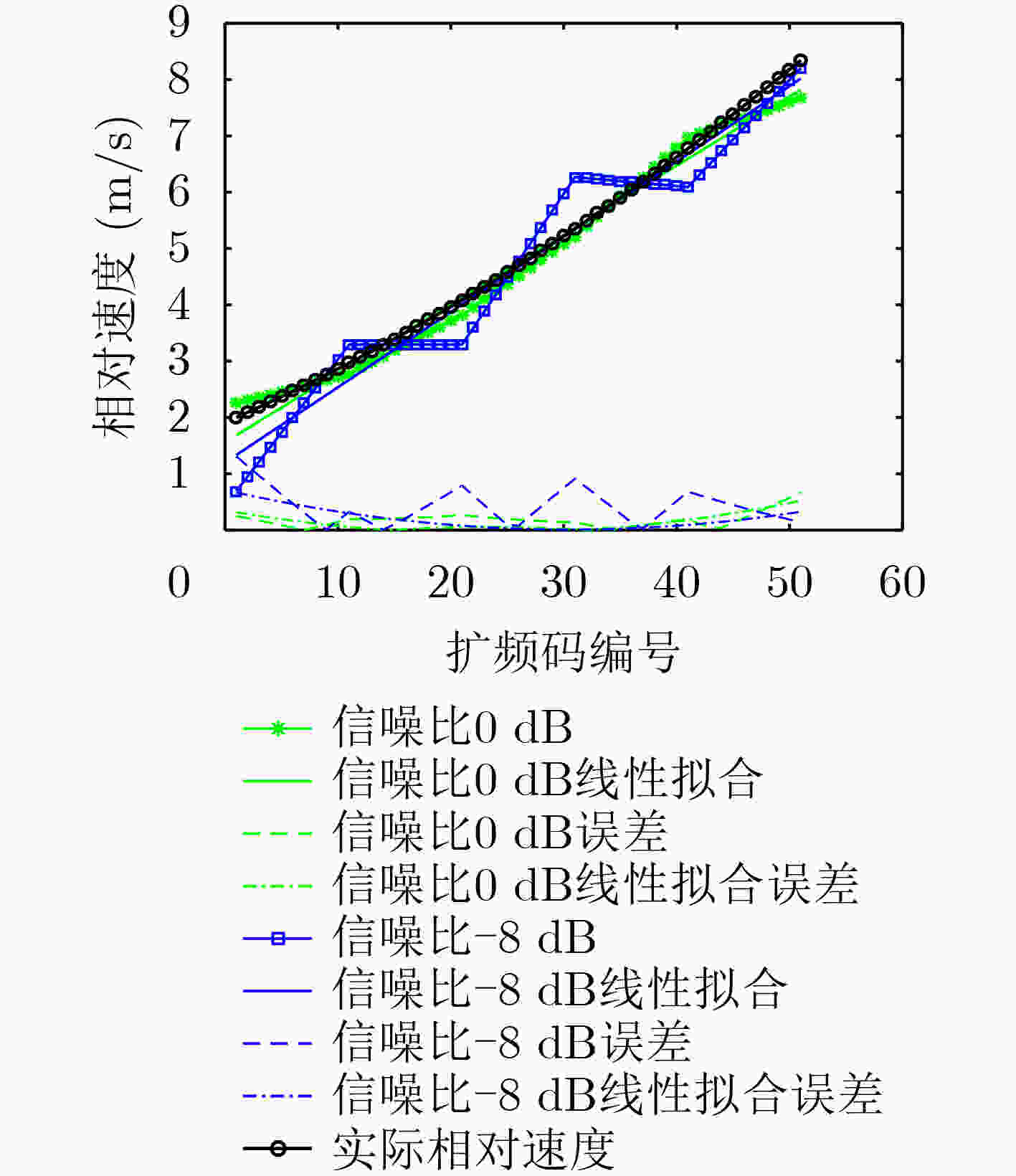
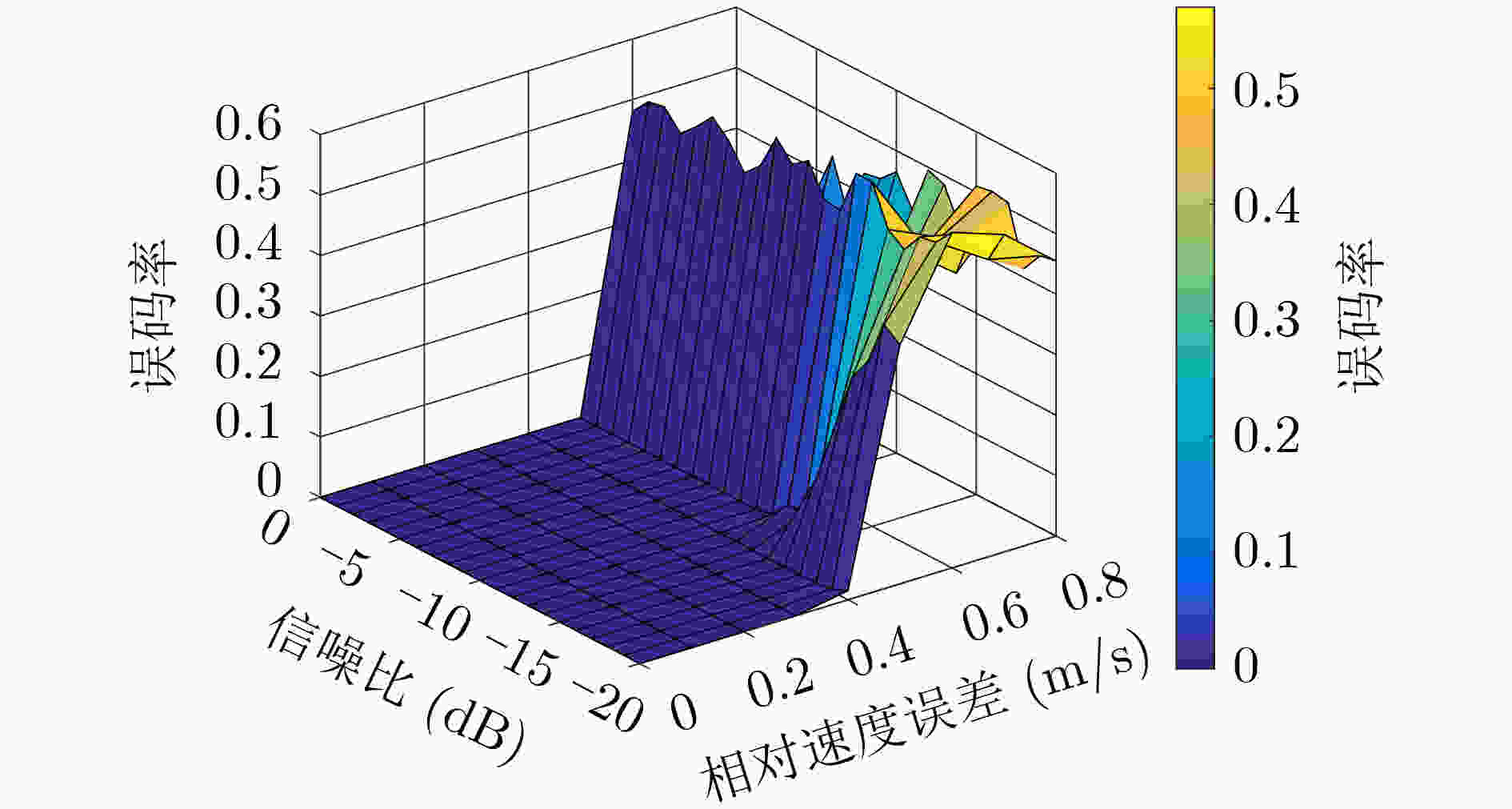
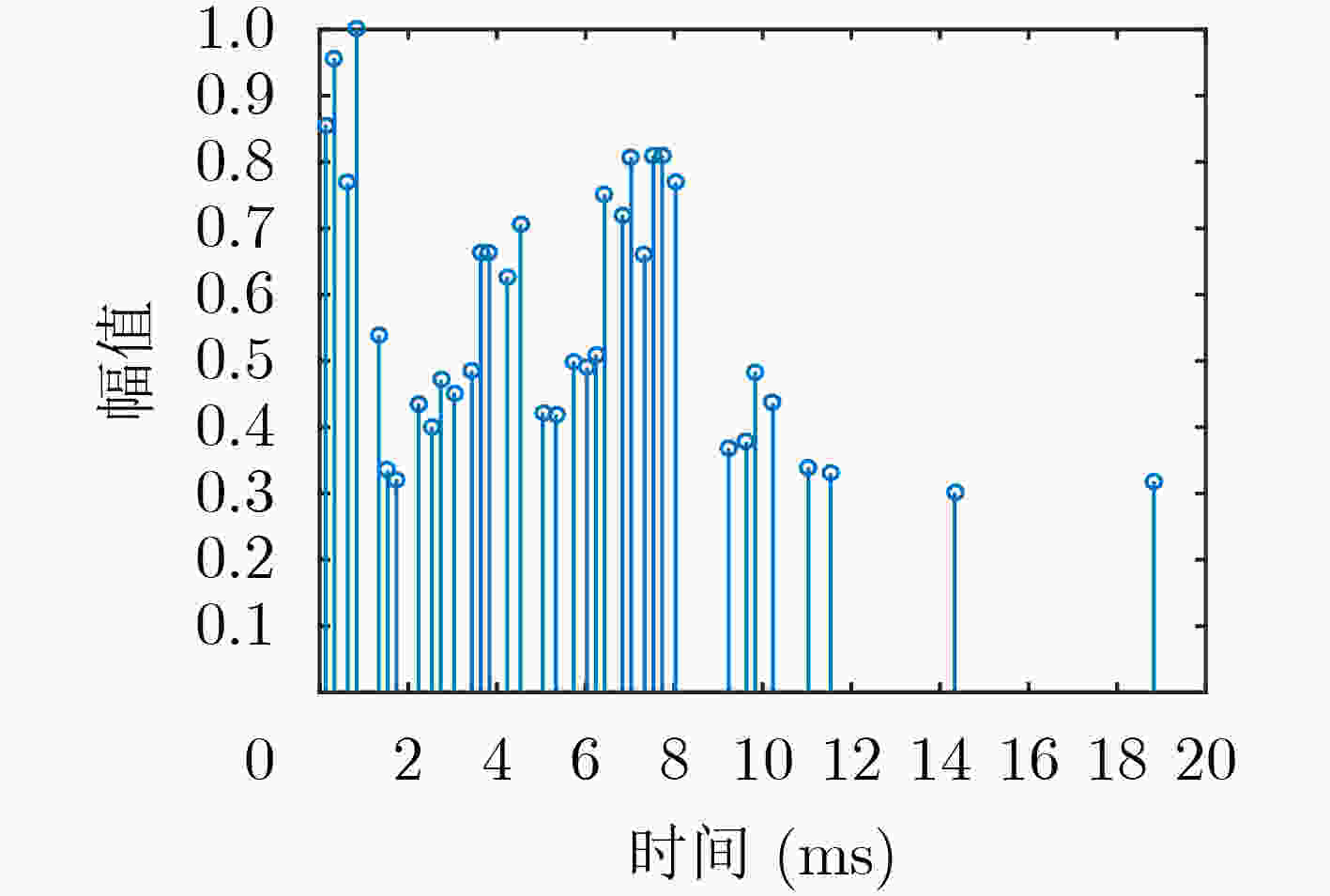
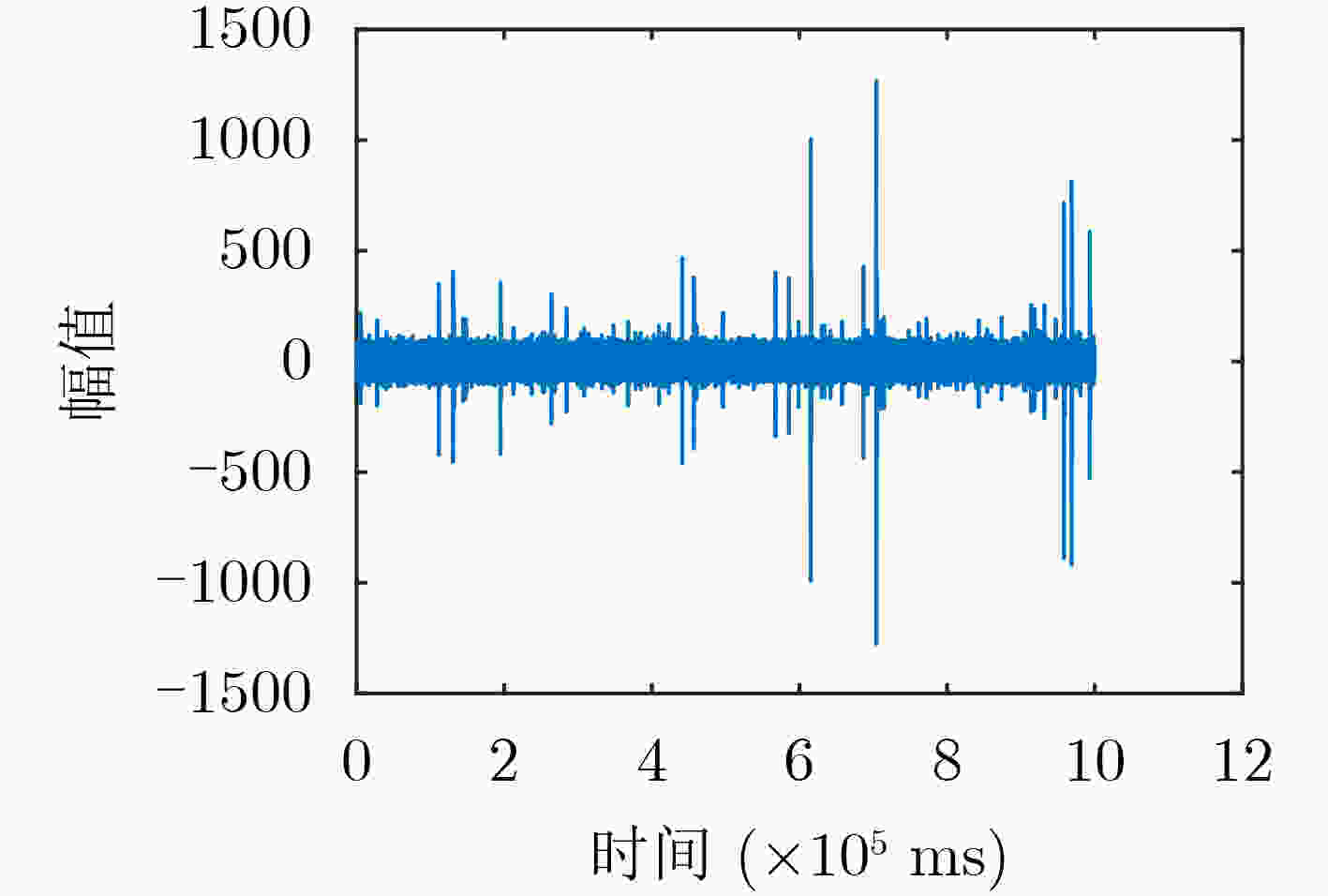
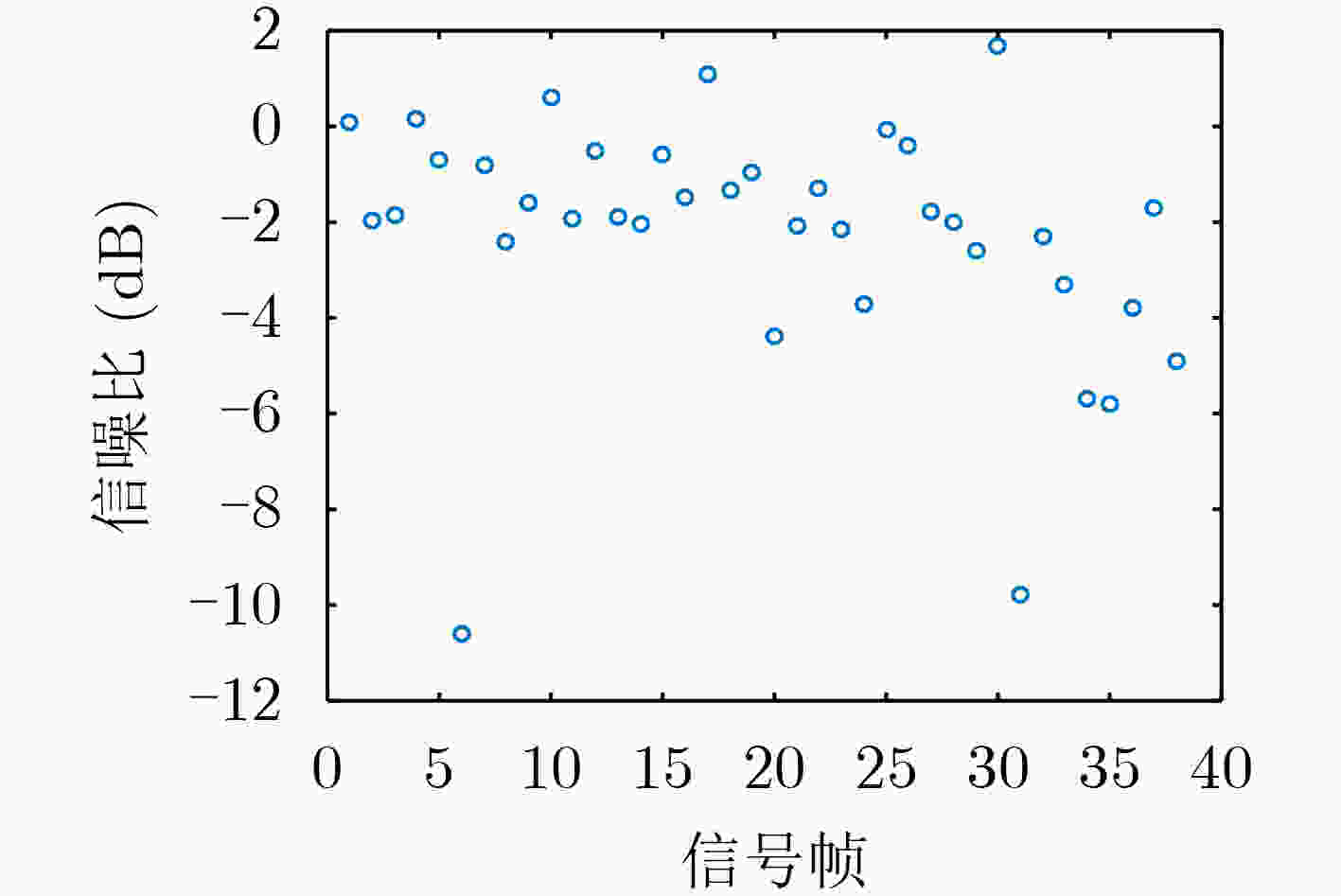
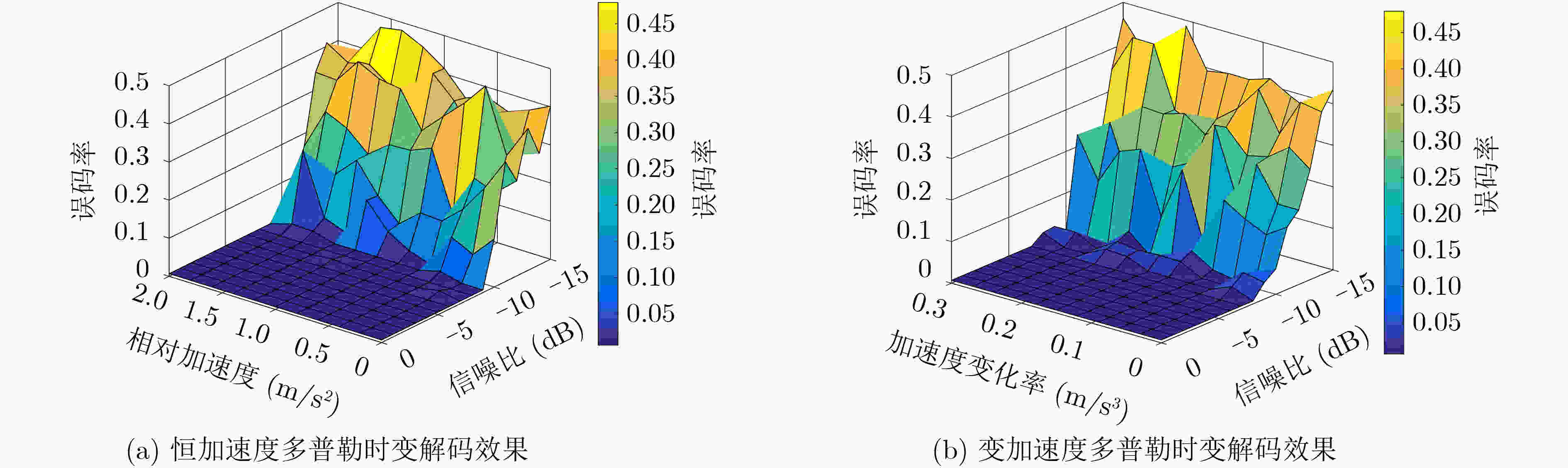
摘要: 针对水下移动平台(AUVs)直接序列扩频(DSSS)水声通信过程中大多普勒时变带来的频偏及载波相位跳变问题,该文提出一种组合差分扩频通信方法。该方法设计一种2维组合差分(TCD)扩频帧结构,接收端通过对重复码时域加窗相关实现时变多普勒粗估计;接收端提出一种频率压缩-能量接收器(FC-ED),通过采用能量检测接收器提高接收端处理多普勒容限,使用频率压缩法多频点压缩处理进一步提高系统鲁棒性,实现扩频码识别映射解码;最后提出一种组合差分算法,实现2维组合扩频间的极性差分解码,在能量接收映射解码基础上引入极性调制,进一步提高频谱利用率。经理论及仿真试验分析,该方法具备一定的抗时变多普勒能力,在恒加速度相对运动–8 dB信噪比条件下误码率小于10–2。Abstract: To deal with the problem of frequency offset and carrier phase fluctuation caused by the conventional Doppler on the DSSS (Direct-Sequence Spread-Spectrum) underwater acoustic communication between AUVs (Autonomous Underwater Vehicles), a combination differential direct sequence spread spectrum algorithm is proposed. The Doppler rough estimation is realized through Two-dimension Combination Difference(TCD) spread spectrum frame structure, and the Doppler tolerance is extended through the Frequency Compression-Energy Detector(FC-ED), then an algorithm of combination differential is proposed for polarity decoding. Using the combination differential direct sequence spread spectrum algorithm, good performance (BEK<10–2) is achieved for a signal-to-noise ratio as low as –8 dB based on at-sea data.
-
表 1 每组码元调制信息比特数
类别 重复码PNs 排列码PNp 组合码PNc 极性调制 映射比特 $ \left\lfloor {{{\log }_2}N} \right\rfloor $ $ \left\lfloor {{{\log }_2}P_N^2} \right\rfloor $ $ (n - 2) \cdot \left\lfloor {{{\log }_2}C_N^2} \right\rfloor $ $ n $ 本文特例 5 10 72 10 -
[1] YANG T C and YANG Wenbin. Performance analysis of direct-sequence spread-spectrum underwater acoustic communications with low signal-to-noise-ratio input signals[J]. The Journal of the Acoustical Society of America, 2008, 123(2): 842–855. doi: 10.1121/1.2828053 [2] YANG T C and YANG Wenbin. Low probability of detection underwater acoustic communications using direct-sequence spread spectrum[J]. The Journal of the Acoustical Society of America, 2008, 124(6): 3632–3647. doi: 10.1121/1.2996329 [3] YANG T C. Properties of underwater acoustic communication channels in shallow water[J]. The Journal of the Acoustical Society of America, 2011, 131(1): 129–145. doi: 10.1121/1.3664053 [4] FREITAG L and STOJANOVIC M. MMSE acquisition of DSSS acoustic communications signals[C]. Oceans '04 MTS/IEEE Techno-Ocean '04 (IEEE Cat. No. 04CH37600), Kobe, Japan, 2004: 14–19. [5] 殷敬伟, 杜鹏宇, 张晓, 等. 基于单矢量差分能量检测器的扩频水声通信[J]. 物理学报, 2016, 65(4): 044302. doi: 10.7498/aps.65.044302YIN Jingwei, DU Pengyu, ZHANG Xiao, et al. Direct-sequence spread-spectrum underwater acoustic communication based on single vector differential energy detector[J]. Acta Physica Sinica, 2016, 65(4): 044302. doi: 10.7498/aps.65.044302 [6] 杜鹏宇, 郭龙祥, 殷敬伟, 等. 基于改进差分能量检测器的移动直扩水声通信研究[J]. 通信学报, 2017, 38(3): 144–153. doi: 10.11959/j.issn.1000-436x.2017058DU Pengyu, GUO Longxiang, YIN Jingwei, et al. Mobile direct-sequence spread-spectrum underwater acoustic communication based on improved differential energy detector[J]. Journal on Communications, 2017, 38(3): 144–153. doi: 10.11959/j.issn.1000-436x.2017058 [7] 夏高峰, 罗宇, 金哲仕. 多进制直接序列扩频系统性能分析及仿真[J]. 航空电子技术, 2015, 46(2): 12–15,20. doi: 10.3969/j.issn.1006-141X.2015.02.06XIA Gaofeng, LUO Yu, and JIN Zheshi. Performance analysis and simulation of M-ary direct sequence spread spectrum system[J]. Avionics Technology, 2015, 46(2): 12–15,20. doi: 10.3969/j.issn.1006-141X.2015.02.06 [8] 郭淑霞, 董文华, 张磊, 等. 混合混沌多进制扩频系统的蒙特卡罗分析[J]. 北京理工大学学报, 2016, 36(7): 760–764. doi: 10.15918/j.tbit1001-0645.2016.07.019GUO Shuxia, DONG Wenhua, ZHANG Lei, et al. Monte carlo analysis of mixed chaotic M-ary direct sequence spread spectrum system[J]. Transactions of Beijing Institute of Technology, 2016, 36(7): 760–764. doi: 10.15918/j.tbit1001-0645.2016.07.019 [9] 殷敬伟, 王蕾, 张晓. 并行组合扩频技术在水声通信中的应用[J]. 哈尔滨工程大学学报, 2010, 31(7): 958–962. doi: 10.3969/j.issn.1006-7043.2010.07.023YIN Jingwei, WANG Lei, and ZHANG Xiao. The application of parallel combinatory spread spectrum in underwater acoustic communication[J]. Journal of Harbin Engineering University, 2010, 31(7): 958–962. doi: 10.3969/j.issn.1006-7043.2010.07.023 [10] KADDOUM G, AHMED M F A, and NIJSURE Y. Code index modulation: A high data rate and energy efficient communication system[J]. IEEE Communications Letters, 2015, 19(2): 175–178. doi: 10.1109/LCOMM.2014.2385054 [11] KADDOUM G, NIJSURE Y, and TRAN H. Generalized code index modulation technique for high-data-rate communication systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7000–7009. doi: 10.1109/TVT.2015.2498040 [12] 葛利嘉, 江治林, 冯胜, 等. 非正交-码索引调制方法[J]. 电子与信息学报, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023GE Lijia, JIANG Zhilin, FENG Sheng, et al. Non-orthogonal-code index modulation[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023 [13] 钟宏伟. 国外无人水下航行器装备与技术现状及展望[J]. 水下无人系统学报, 2017, 25(3): 215–225. doi: 10.11993/j.issn.2096-3920.2017.03.001ZHONG Hongwei. Review and prospect of equipment and techniques for unmanned undersea vehicle in foreign countries[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 215–225. doi: 10.11993/j.issn.2096-3920.2017.03.001 [14] 王童豪, 彭星光, 潘光, 等. 无人水下航行器的发展现状与关键技术[J]. 宇航总体技术, 2017, 1(4): 52–64.WANG Tonghao, PENG Xingguang, PAN Guang, et al. Development and key technologies of unmanned underwater vehicles[J]. Astronautical Systems Engineering Technology, 2017, 1(4): 52–64. [15] KIM B and KONG S H. Determination of detection parameters on TDCC performance[J]. IEEE Transactions on Wireless Communications, 2014, 13(5): 2422–2431. doi: 10.1109/twc.2014.0204014.131704 [16] 刘晓明, 张鹤, 吴皓威, 等. 高动态环境下长码扩频信号快捕算法[J]. 电子与信息学报, 2016, 38(6): 1398–1405. doi: 10.11999/JEIT150860LIU Xiaoming, ZHANG He, WU Haowei, et al. Rapid DSSS signal acquisition algorithm under high dynamic environment[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1398–1405. doi: 10.11999/JEIT150860 -





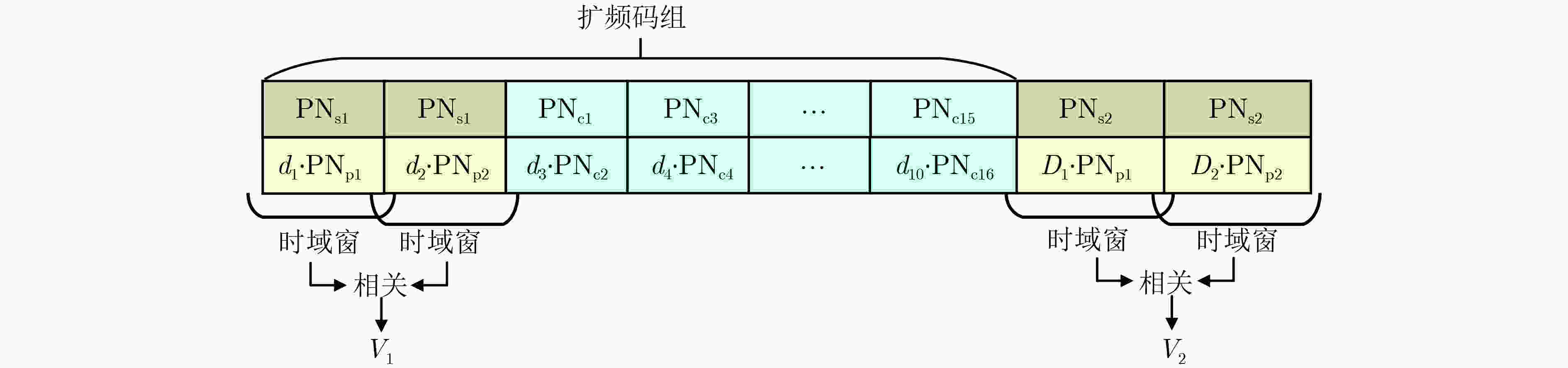
 下载:
下载:
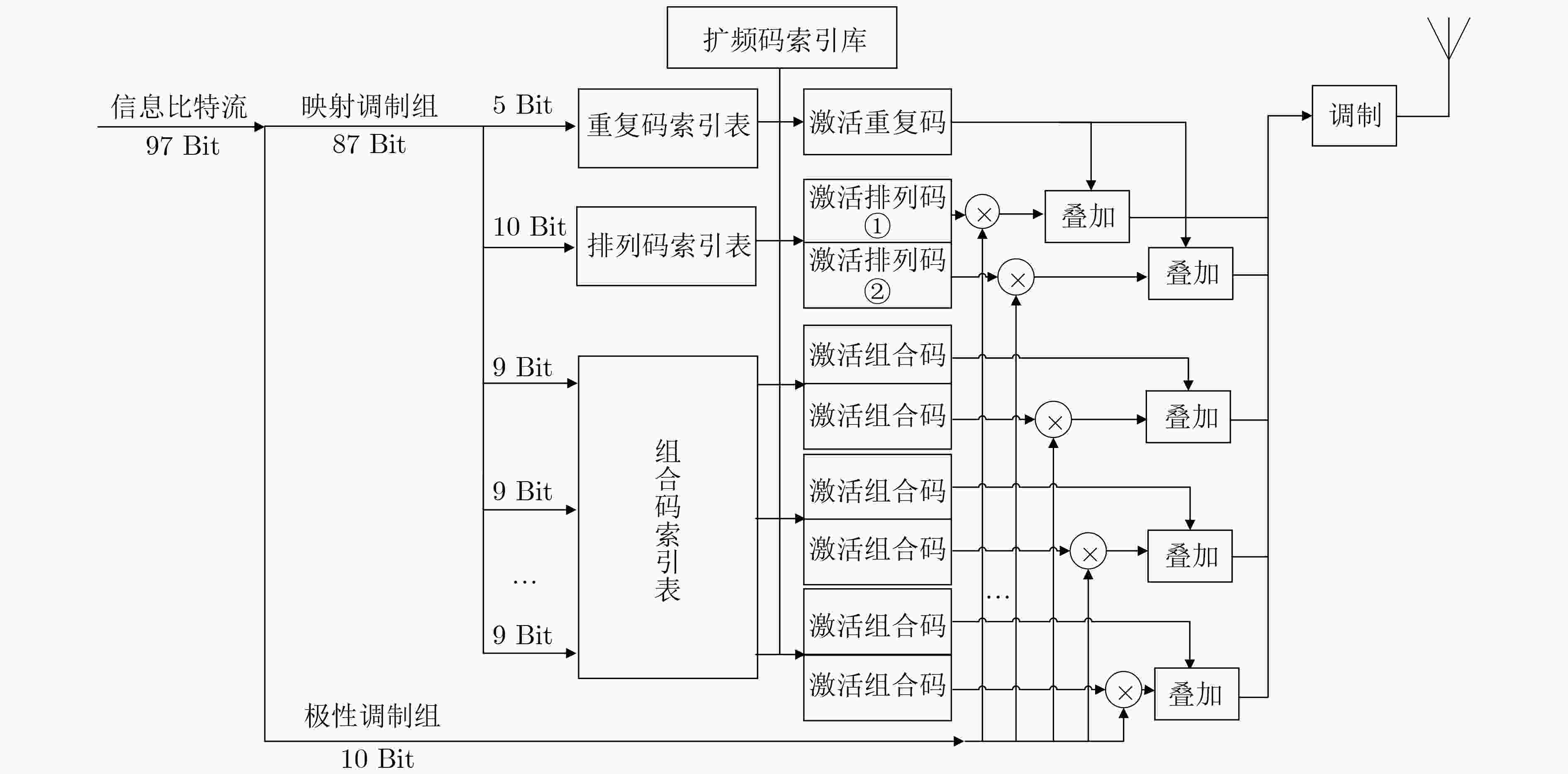
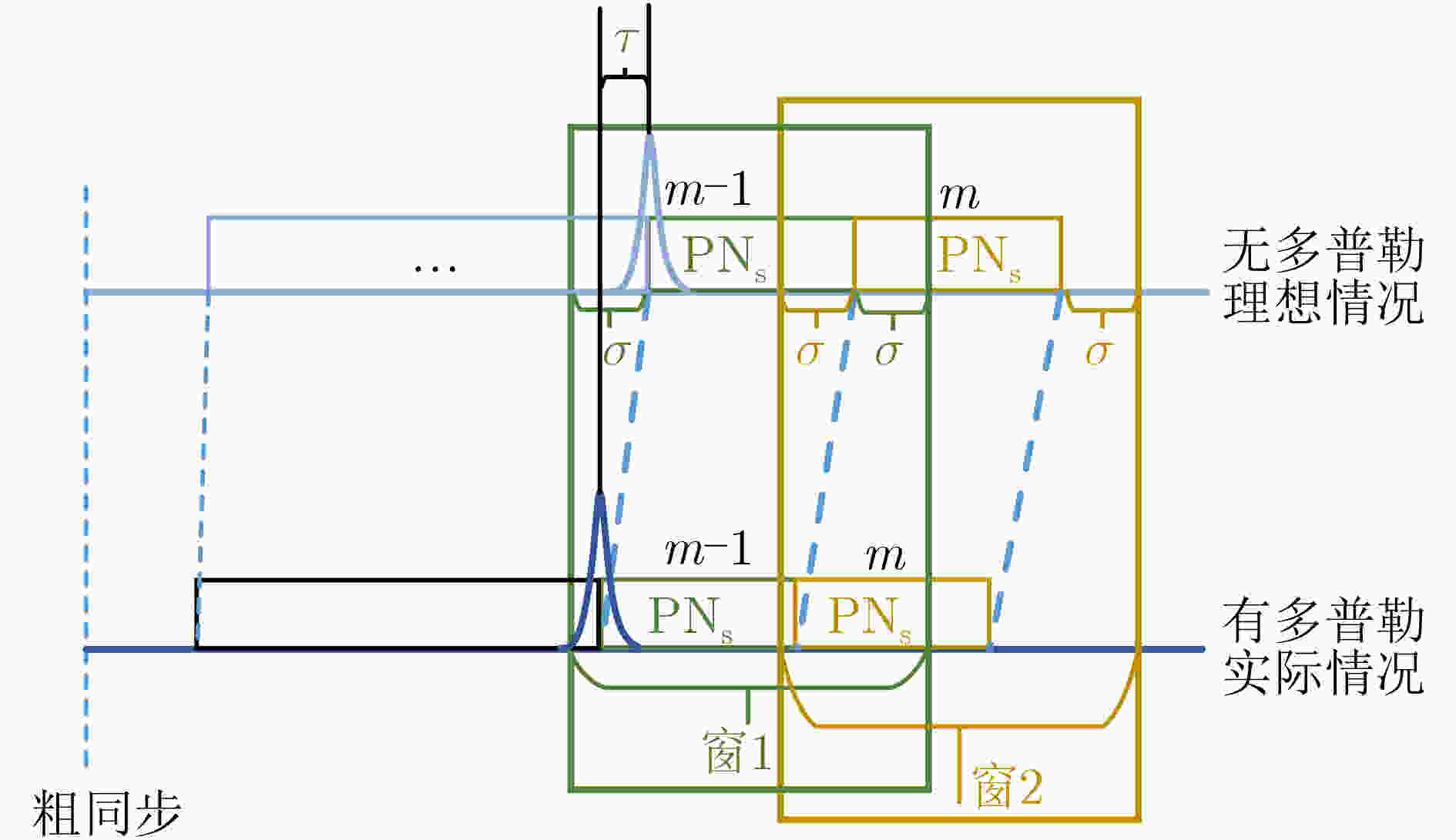
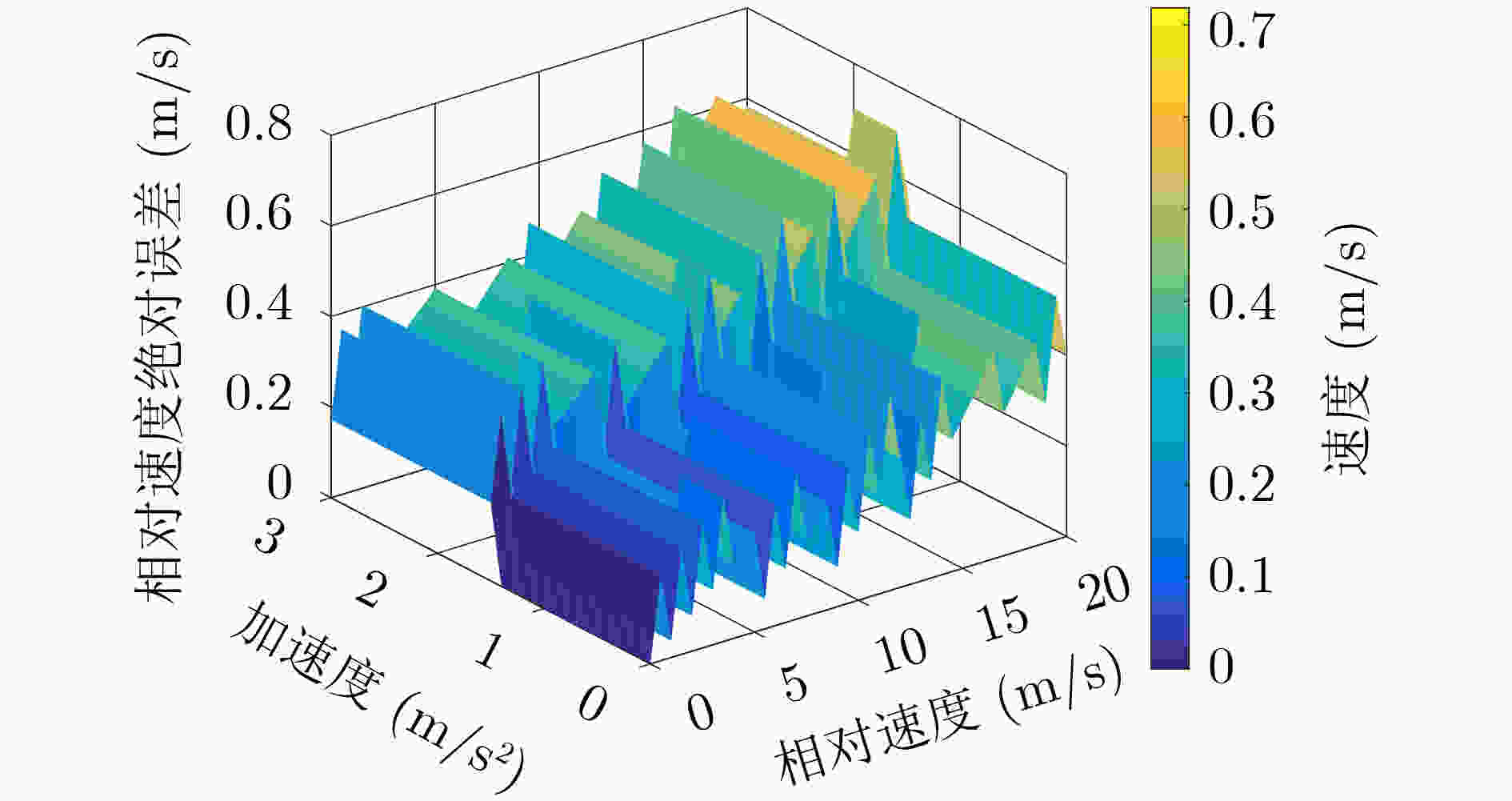
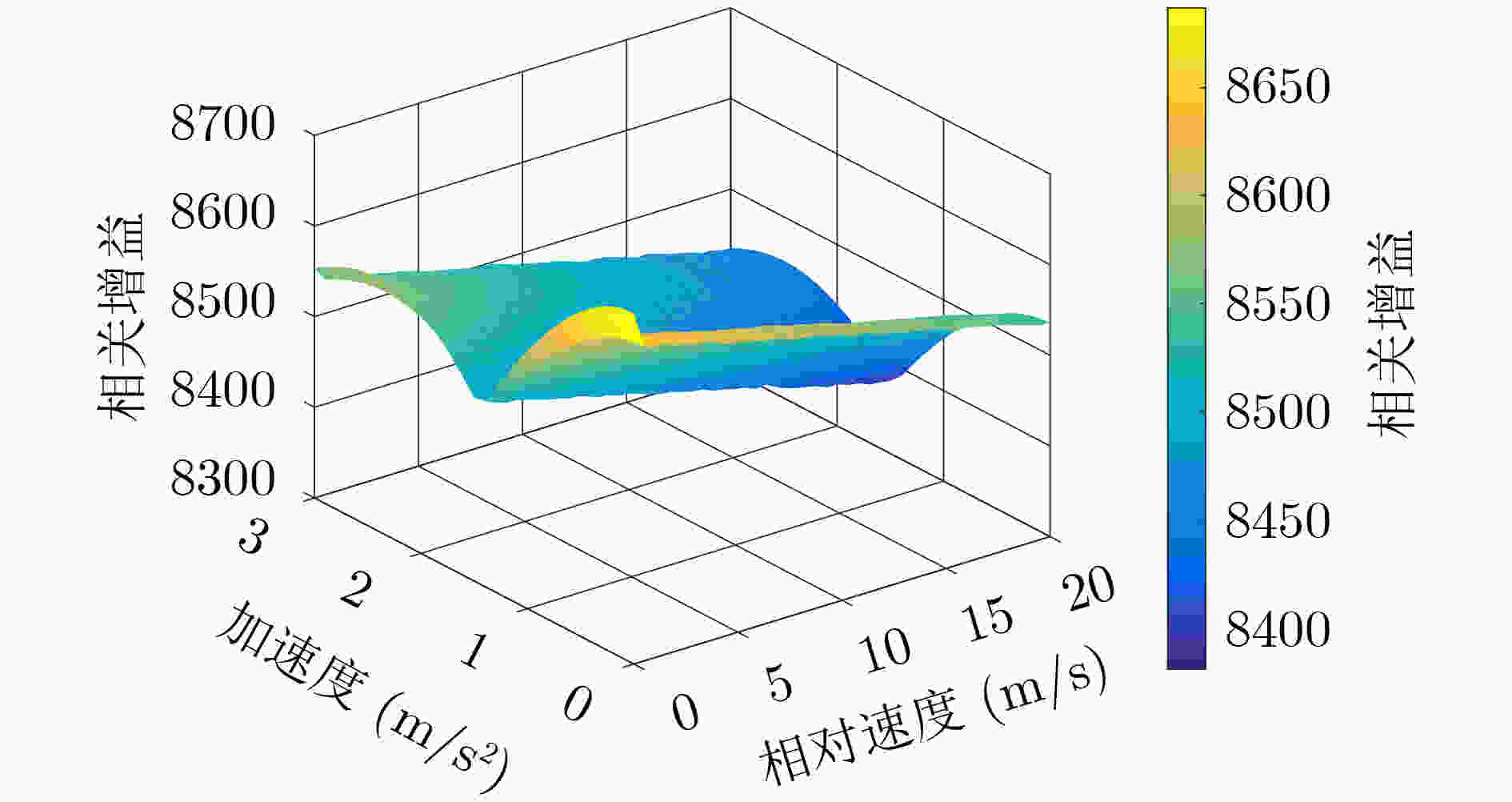
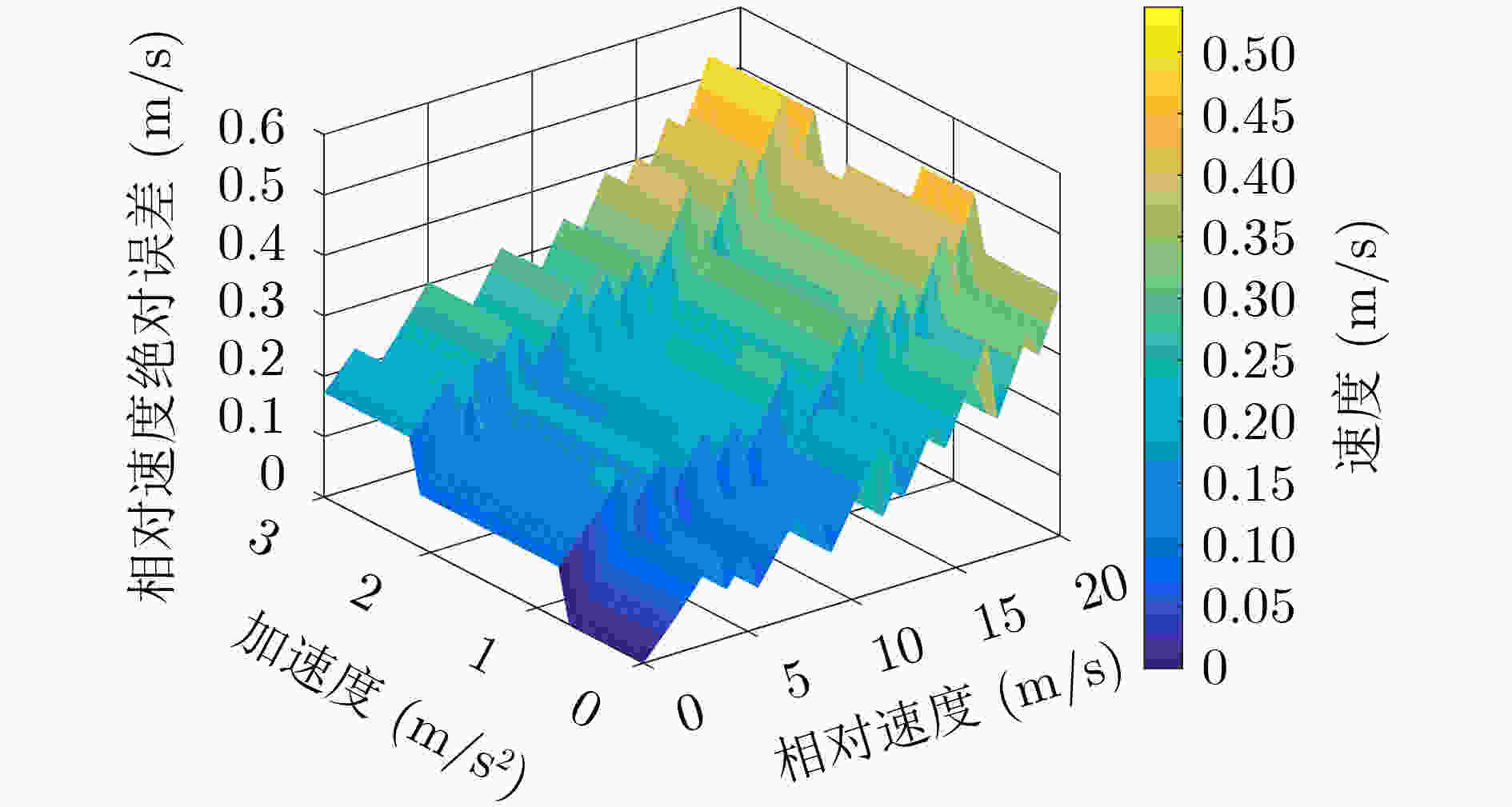
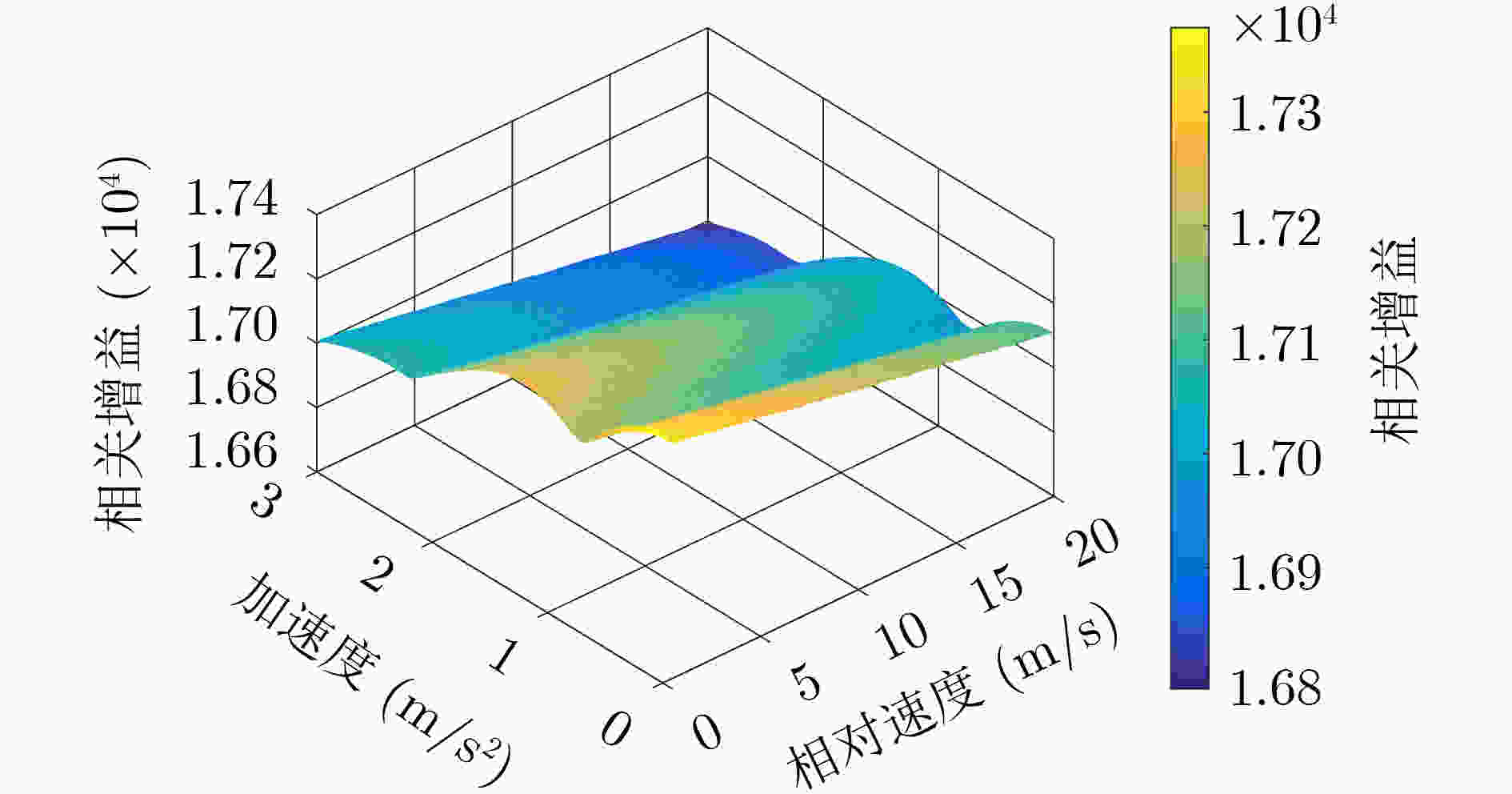
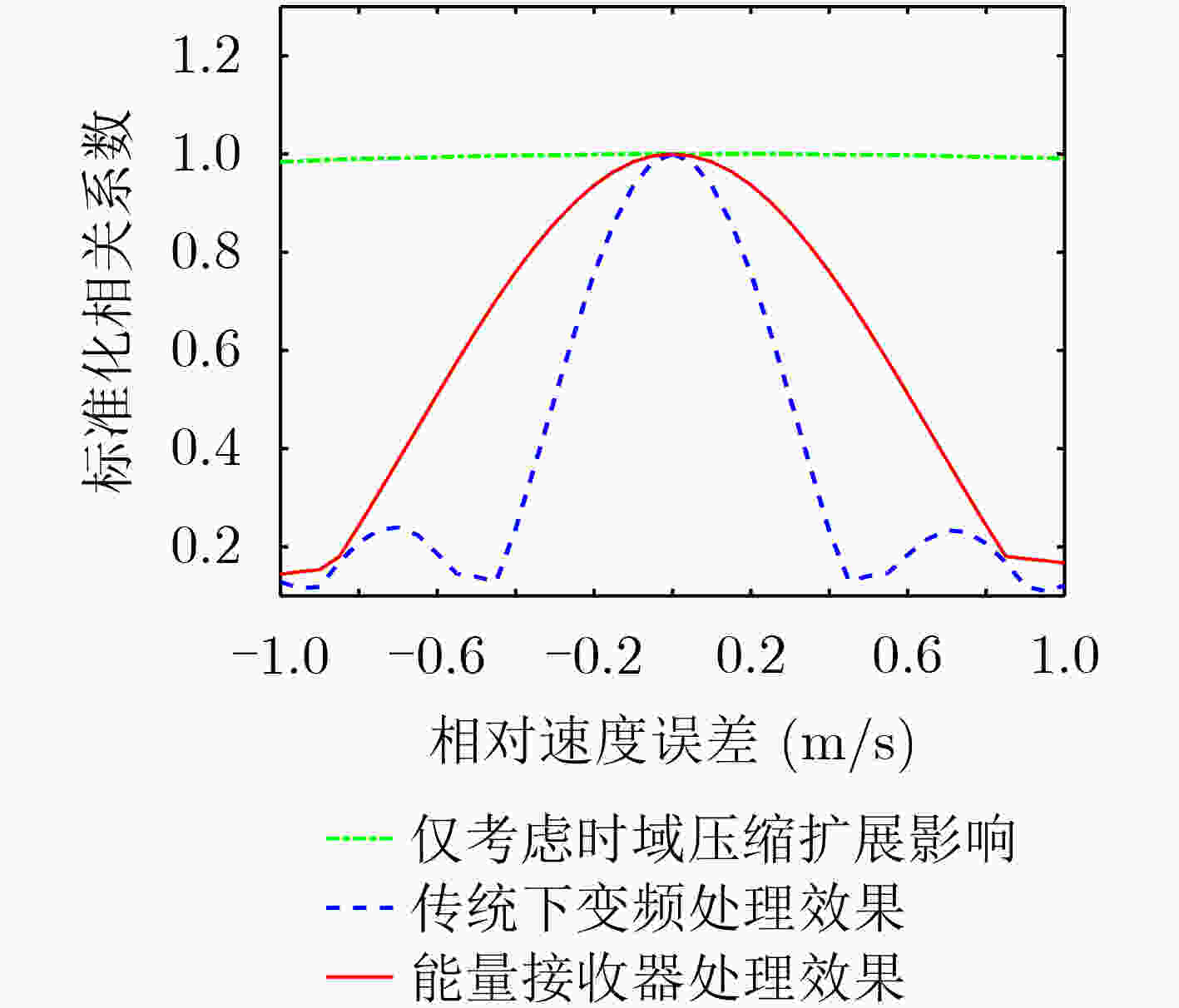


 下载:
下载:
