Tsallis Entropy Thresholding Based on Multi-scale and Multi-direction Gabor Transform
-
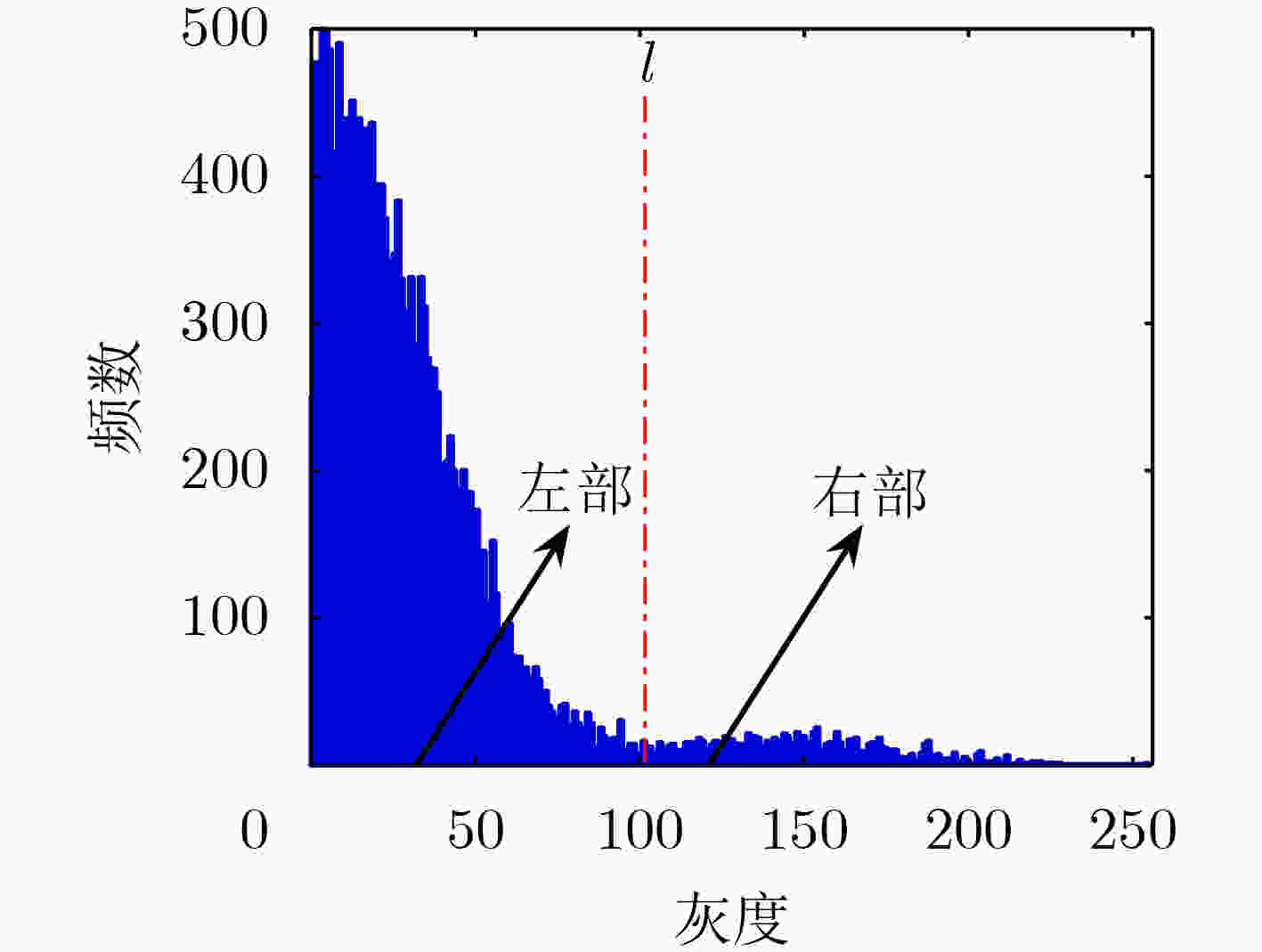
摘要: 为了能在统一框架内处理无模态、单模态、双模态或者多模态直方图情形下的自动阈值选取问题，该文提出一种基于多尺度多方向Gabor变换的Tsallis熵阈值分割方法(MGTE)。该方法先通过Gabor变换得到多尺度乘积图像，然后利用内外轮廓图像从多尺度乘积图像中重构1维直方图，并在重构1维直方图上采用Tsallis熵计算模型来选取4个方向Tsallis熵取最大值时对应的阈值，最后对4个方向的阈值进行加权求和作为最终分割阈值。将提出的方法和5个分割方法在4幅合成图像和40幅真实世界图像上进行了实验。结果表明提出的方法虽然计算效率不占优势，但它的分割适应性和分割精度有明显的提高。Abstract: To deal with automatic threshold selection issue in non-modal, unimodal, bimodal or multimodal situations within a unified framework, a Tsallis Entropy thresholding segmentation method based on Multi-scale and multi-direction Gabor transform (MGTE) is proposed. The multi-scale product image is first obtained by the Gabor transform and then the inner and outer contour images are used to reconstruct the one-dimensional histogram from the multi-scale product image. Based on the reconstruction of the one-dimensional histogram, the Tsallis entropy calculation model is utilized to select 4 thresholds by maximizing Tsallis entropy in 4 different directions, and finally the weighted sum of the 4 thresholds is used as the final threshold. The proposed method is compared with 5 segmentation methods on 4 synthetic images and 40 real-world images. The results show that the proposed method has no advantage in computational efficiency, but its adaptability and segmentation accuracy are significantly improved.
-
1. 引言
静电放电具有瞬时电压高、能量大、不易察觉等特点，容易对集成电路、石油化工、航天、工业生产等多个领域产生严重的危害[1-5]。静电测量是检测人体、物品及环境等是否带电最直接的手段，可用于评估静电防护的效果，研究静电积累及放电机理等，对于静电防护具有重要意义。基于电场感应原理对带电物表面电位进行非接触测量，具有不干扰被测表面、测试过程无电荷转移风险等优点，是近年来静电防护领域的研究热点之一[6]。
按照检测原理划分，非接触式静电仪可分为高阻式、场磨式、振动电容式及微机电式等。高阻式静电压仪利用高输入阻抗的直流放大电路进行测量[7]，测量过程中感应电荷在放大电路中随时间衰减，造成测试结果不稳定，需要定期清零，影响测量的稳定性。场磨式电场仪采用电机带动屏蔽电极旋转，周期性地屏蔽感应电极，从而将感应电极的感应电荷调制成交流信号，避免了信号衰减，提升了测试精度[8,9]。由于存在电机驱动、旋转叶片等数十个机械结构，组装工艺复杂，不利于批量化制造，电机旋转磨损造成寿命衰减。振动电容式静电计通过压电陶瓷片驱动感应电极振动，从而在感应电极上产生交流感应信号[10,11]，具有体积小、重量轻等优点，在非接触静电测量领域广泛应用。然而，压电材料在长期工作时，温度变化影响压电常数和弹性模量，造成压电悬臂梁谐振频率和振幅发生改变，影响长期稳定性[12]。此外，场磨式、振动电容式两种静电仪均存在裸露的可动部件，容易受机械碰撞、粉尘、油气等影响而发生失效。随着微机电系统(Micro Electro Mechanical Systems, MEMS)技术的发展，人们采用硅微工艺制备出振动结构，实现了感应信号的周期性调制，研制出MEMS电场传感器，具有体积小、可批量化制备，无机械磨损、寿命长，封装后无裸露可动部件、可靠性高等多种突出优点[13-16]，在静电测量领域具有广阔的发展前景。本团队曾于2017年报道一种基于MEMS电场敏感芯片的静电测量装置，实现测量人体不同部位带电分布的非接触式测量[17]。
通过标定实现电场到被测表面电位的转换，对保证非接触式静电仪的测量精度十分重要。传统的场磨式及振动电容式静电仪均采用固定距离的方式进行表面电位测量。例如，日本SIMCO公司的FMX-004型、美国MONROE公司的282A型等，通过两个光斑重合的方式将测试距离固定为2.54 mm。德国Kleinwachter公司的EFM-022型测试仪利用两根已知长度的绝缘棒固定测试距离。美国TREK公司的520型测试仪将探头设计成尖端形状，可实现在5～25 mm小范围内的测量。然而，当测试距离改变时，到达传感器的电场强度发生改变，造成灵敏度变化，影响测试精度。文献[17]介绍了一种用于测量人体静电的门体结构，采用两个相对布置的检测电极，通过共模运算解决了被测人体未居中造成的误差问题，然而，对于不同体型的测试人员，仍存在测试距离不一致的难题，带来测试误差。在被测物难以维持静止或不容易靠近等复杂环境下，固定距离可能对测试带来不便。此外，带电物尺寸不同，产生的电场分布也不相同，在固定距离下测试也容易造成偏差。难以实现动态距离测试、对被测物尺寸缺乏标定，是目前非接触式表面电位测量面临的问题。
本文基于MEMS电场传感器，开展非接触式表面静电测量技术研究，区别于传统的定距测量方案，提出距离可变的测量思路，研究静电仪的动态标定及测试方法，实现距离自适应的表面静电位准确测量。本文为复杂环境下非接触表面静电测试提供新的思路，从而进一步提升静电敏感领域的静电防护效果，为集成电路、石油化工、航天等多种高端产品制造过程提供先进技术手段。
2. MEMS电场敏感芯片
本文采用谐振式共面电极型MEMS电场敏感芯片，总体尺寸为5 mm×5 mm×0.5 mm，结构如图1所示，主要包括屏蔽电极、感应电极、驱动电极、弹性折梁等几部分，屏蔽电极与弹性折梁相连构成水平振动微结构。通过在驱动电极上施加交流电压信号，驱动电极与屏蔽电极之间产生交变静电吸合力，带动屏蔽电极进行周期性水平振动。驱动电极与屏蔽电极设计成梳齿形状，用于增加二者之间的电容，从而增加静电力。当屏蔽电极振动时，周期性地屏蔽感应电极，在静电场及屏蔽电极的共同作用下，感应电极上感生出正比于被测电场的交流感应信号。屏蔽电极与感应电极相互作用部分也设计成交错梳齿形状，与条形结构相比，增大了二者之间的电容，从而增大了屏蔽与暴露的效率。感应电极设计为两组，受屏蔽电极交替屏蔽，产生相位差为180°的差分信号，通过差分减小电路噪声，提升信噪比。与场磨式电场仪相比，MEMS谐振式敏感芯片无电机等易磨损器件，寿命长，工作过程具有更好的稳定性及更高的可靠性。与采用压电陶瓷的振动电容式传感器相比，避免了长期工作时压电常数和弹性模量的温度漂移，长期稳定性更好。
敏感芯片的振动特性符合如图2所示的2阶动力学模型。其中，ks, meff, cc, cs,strip分别为传感器谐振状态下的等效弹性系数、质量、滑膜阻尼及压膜阻尼。目前，敏感芯片工作在开环状态，通过扫频确定芯片的谐振点：在不同的频率下，读取敏感芯片的输出本底值(由驱动电极产生本底电场，感应电极在该本底电场下产生输出信号)，峰值所对应的频率即为敏感芯片的谐振频率。
MEMS电场敏感芯片采用绝缘体上硅(Silicon-On-Insulator, SOI)晶圆制备，屏蔽电极、感应电极、驱动电极、弹性折梁等几部分在同一结构层，工艺简单，成品率高。工艺流程图如图3所示。
具体的流程如下：
(1) 硅掺杂：采用1层磷硅酸玻璃(PhosphoSilicate Glass, PSG)沉积在器件层的表面，并退火1 h，然后用湿法化学腐蚀方法去除PSG层；
(2) 制作焊盘：焊盘由20 nm铬和500 nm金构成，采用第1级掩膜版，通过电子束蒸镀的方法将金属沉积到硅表面；
(3) 器件层图形化：在器件层旋涂UV光刻胶，采用第2级掩膜版，图形化器件层的光刻胶，然后利用等离子深刻蚀(Deep Reactive Ion Etching, DRIE)设备，刻蚀器件层到氧化埋层停止；
(4) 基板层图形化：在已刻蚀完的器件层上旋涂保护材料，采用第3级掩膜版，套刻图形，利用反应离子刻蚀移除基板层底层的氧化层，再用DRIE完整地刻穿基板层至氧化埋层停止；
(5) 释放：移除器件层上的保护材料及氧化埋层。
为了提升敏感芯片的环境适应性及可靠性，本文采用全密封结构的MEMS敏感芯片封装，主要由基板、绝缘层、封装盖等几部分组成，如图4所示。其中，基于绝缘材料的封帽结构将敏感芯片完全密封在微小腔体内，实现了对被测电场信号的传导。E0表示封装外部被测电场，E1表示封装内部到达敏感芯片表面的电场。与敏感结构直接裸露的其他静电仪相比，该结构封装后无裸露可动部件，可耐高湿度、粉尘、碰撞等恶劣条件的影响，使传感器可在户外、粉尘车间等更多工矿条件下使用。
3. 信号处理电路
本文研制的静电仪主要包括MEMS电场敏感芯片、测距模块、信号处理电路、显示屏、蜂鸣器、温湿度传感器、数据存储单元、实时时钟(Real-Time Clock, RTC)、电池等部分，如图5所示。其中，MEMS电场敏感芯片和测距单元位于静电仪前端：通过同时获知电场及距离信息，并利用不同的距离下的标定系数，实现距离可变的表面静电位测量。温湿度传感器主要用于测量环境的温度、湿度，从而对环境是否容易起电、物体是否带电进行评估。RTC时钟用于为整个手持静电仪提供时间信息，便于为数据存储单元上保存的数据标记测试时间。数据存储单元可同时存储时间、电场、距离、温度、湿度、测试电压等信息。显示屏上可实时显示带电体的表面电压、距离等，当测试电压超过预设阈值时，显示屏及蜂鸣器能够实时进行报警。此外，本文研制的静电仪还包括USB充电及数据读取、电池低压报警、自动校零等多种功能，为实际测量提供便利。
在信号处理电路中，通过微控制单元(MicroController Unit, MCU)控制直接数字式频率合成器(Direct Digital Synthesizer, DDS)模块输出正弦信号，为敏感芯片振动提供交流驱动电压，使敏感芯片的屏蔽电极振动。感应电极上产生正比于被测电场的交流电流信号，在I-V模块进行电流电压变换放大，转换成便于采集的交流电压信号。模拟数字转换器(Analog to Digital Converter, ADC)模块用于对放大后的芯片输出信号进行高速采集，进入MCU后进行敏感芯片输出信号的幅值信息处理。根据敏感芯片输出信号为pA～nA级微弱电流信号的特征，芯片的第1级放大拟采用低偏置电流、低偏置电压的轨到轨放大器，并按照图6所示的电路原理图进行信号的I-V转换预处理。其中，Sen_out信号为敏感芯片输出的微弱电流信号，该放大电路的输出信号
Vout=Sen_out×R1 ，C1与R1构成低通滤波器对放大的电压信号进行初步滤波处理。传统静电仪在测量带电物表面静电时，通过两个具有一定夹角光斑重合的方式，固定测试距离，一般为2.54 cm。光斑重合法采用目测观察，可能由于目测重合度不好造成距离误差。固定距离方式也限制了传感器的使用场合，例如，当被测电压较高时，近距离测试可能诱发放电现象，造成仪器损坏或人员触电。当被测物的距离增加时，到达传感器表面的电场减小，造成标定灵敏度衰减，测试结果偏小。为了解决距离变化问题，本文基于超声波原理测距模块，准确获知静电仪与被测物之间的距离，并在不同距离下对传感器进行标定，获知灵敏度与距离的关系。在实际测试时，根据测距结果查找灵敏度数值，计算被测物电压，从而实现了距离可变的自适应测试。本文选用的超声波模块中已对温度漂移进行了补偿，在使用过程中可以忽略温度对测距结果带来的影响。该模块的探测距离范围为2.0 cm～4.5 m，测试精度为0.3 cm。当距离太近时，测量结果偶尔出现较大偏差，可能是由于超声波探头与被测物之间形成的驻波造成的；当距离太远时，测量环境中其他物体可能对电场分布产生干扰，影响测量精度。因此，在实际使用中对测量距离限定在2.5～10 cm，当超过该范围时通过显示屏进行适当提醒。
本文研制出了手持式的静电仪，电场探测电极及超声波测距单元位于最前端，面向被测带电体。通过正面的显示屏及按键，进行测试、存储等功能操作。
4. 标定与现场校准
由于带电人体、固体等被测物形貌及材料不同，产生非匀强电场，静电仪实际感应到的为畸变电场。为了实现对被测物携带静电电压、电荷等的准确测量，本文对静电仪进行实验室及现场两次标定。
实验室标定采用平行极板结构的电场箱完成。其中，一组极板接地，另一组极板接高压。静电仪固定在接地极板上，与高压极板之间的距离为20 cm。在高压极板上施加0～12 kV的电压，从而在两极板之间产生0～60 kV/m的匀强电场。标定过程记录静电仪输出与高电压之间的线性关系。
E=(Vout−Vo)/k (1) 其中，E为被测电压值；Vout为静电仪输出原始值；Vo为静电仪电场零点标定值；k为静电仪的实验室灵敏度系数。
标定时，共施加6个行程(3个正行程，3个反行程)，记录每个电场下的静电仪原始输出结果(单位为mV)，进行直线拟合。其中，每个测试电场下共记录6次测试结果。标定结果如图7所示，根据GB 18459计算，传感器的总不确定度为2.98%。由于传感器信号解调时包含与驱动信号相关的相位差信息，输出结果也有可能为负值，本次标定出的传感器灵敏度k为正。
静电仪的现场标定装置主要包括带电极板、带电极板支架、直线导轨、高压源表及计算机等几部分。其中，静电仪固定在直线导轨上方，与带电极板垂直放置，通过导轨的平移改变静电仪与带电极板之间的距离。在带电极板(标准待测物)上施加一个已知电压VC，通过静电仪的输出结果及式(1)，得到校准前测试电压VC0，则现场灵敏度系数
C=VC0/VC ，静电仪的灵敏度由原来的k校准为k×C。即待测电压E=(Vout−Vo)/(kC) (2) 静电仪的现场校准系数与被测物尺寸、测试距离两个关键因素相关。为了研究这一规律，本文加工了不同尺寸的金属圆板作为高压极板，用于模拟不同的被测物尺寸，并在不同测试距离下对静电仪进行标定，获取了直径为15～80 cm金属圆板现场灵敏度系数动态关系，部分结果如图8所示。可以看出，被测物尺寸越小、距离越远，电场衰减越严重，需要进行修正的现场灵敏度系数越高。通过该图也可以反映测距误差对于灵敏度选择的影响，例如，当测试距离为10 cm、被测物直径为50 cm时，0.3 cm的测距误差可造成约1.38%的灵敏度误差。
参考《JJF 1517-2015 非接触式静电电压测量仪校准规范》，本文将研制出的非接触式静电仪在北京东方计量测试研究所进行了检测(检测证书编号：DY19-1982)。分别选取2 cm, 5 cm, 10 cm 3个测试距离，施加不同的测试电压，记录静电仪输出与实际施加电压的偏差情况，结果如表1所示。测试结果表明，本文研制的非接触式静电仪可实现动态距离的表面电位测量，测量平均误差为–2.98%，最大误差为-10%。
表 1 静电仪第三方校准结果测试距离 2 cm 5 cm 10 cm 标准值(kV) 示值(kV) 相对误差(%) 示值(kV) 相对误差(%) 示值(kV) 相对误差(%) 0.50 0.51 +2.00 0.49 –2.00 0.50 0.00 1.00 1.03 +3.00 0.97 –3.00 0.99 –1.00 2.00 2.09 +4.50 1.95 –2.50 2.00 0.00 2.50 2.59 +3.60 2.43 –2.80 2.48 –0.80 3.00 3.10 +3.33 2.93 –2.33 2.99 –0.33 4.00 4.15 +3.75 3.94 –1.50 3.99 –0.25 5.00 5.36 +7.20 4.93 –1.40 4.98 –0.40 –0.50 –0.55 –10.00 –0.53 –6.00 –0.53 –6.00 –1.00 –1.09 –9.00 –1.07 –7.00 –1.06 –6.00 –2.00 –2.20 –10.00 –2.15 –7.50 –2.15 –7.50 –2.50 –2.58 –3.20 –2.67 –6.80 –2.61 –4.40 –3.00 –3.26 –8.67 –3.22 –7.33 –3.09 –3.00 –4.00 –4.29 –7.25 –4.28 –7.00 –4.09 –2.25 –5.00 –5.41 –8.20 –5.32 –6.40 –5.03 –0.60 5. 结束语
本文提出并研制了一种距离可变的非接触式表面静电仪。与传统定距测量模式相比，具有使用场景更加广泛、可靠性更好等优点。在进行第三方检测时，误差最大可达–10%。误差主要来源于以下4个方面。(1)测量距离误差：本文采用超声波反射原理获知被测物距离，在测试距离较小时，容易因超声波多次反射，造成距离误差，从而对表面电位造成误差。(2)角度误差：在静电仪标定及实际测试时，理想情况是静电仪与被测表面垂直，然而实际摆放的垂直度存在偏差，影响电场分布以及测距结果，从而造成最终结果偏差。(3)静电荷干扰：在静电仪测试时，由于感应电极上的静电未消除干净，造成零点存在偏差，正负电压的测试误差存在细微的差别。在实际使用时，如果被测物为非平面结构，例如球面、凸起的尖端等，则不适用于图8所示的标定结果，需要针对被测物形貌进行现场标定。(4) 受到温度变化的影响，图2中传感器的等效弹性系数kx，以及受气压变化造成空气阻尼cc, cs,strip的变化，均可能造成敏感芯片谐振频率的改变，从而造成测量结果的温度漂移。通过在不同温度下记录传感器的灵敏度和零点，从而标定出传感器的温度漂移规律，在测量时通过嵌入式软件进行温度补偿，可以消除一部分温度的影响。在实际使用时，在该手持式静电仪上增加了校零功能，在使用前使静电仪测量零电位校准零点，也可以抑制部分温度的影响。
此外，第三方检测施加电压的范围为–5～5 kV，与传统静电仪相比量程偏小。其原因在于，为了提高静电仪在小电压的测量精度，本文增大了静电仪外部感应电极尺寸，从而提升响应信号大小。当被测电场过大时，可能造成局部饱和。在需要测量更大电压时，可通过增加测试距离的方法来解决。
静电测量是静电防护的重要组成部分。本文基于MEMS电场芯片技术，研制出距离可动态适应的非接触式静电仪，与传统静电仪相比，具有以下创新之处：(1)基于MEMS电场敏感元件，具有体积小、功耗低、易集成、可批量化制备等突出优点。(2)设计了敏感元件封装，与传统振动电容式、场磨式静电仪相比，无裸露可动部件，可靠性高。(3)提出动态标定算法，克服了距离变化对测量结果的影响。经第三方检测，本文研制的静电仪在2 cm, 5 cm, 10 cm 3个距离下，平均测试误差为–2.98%。
-
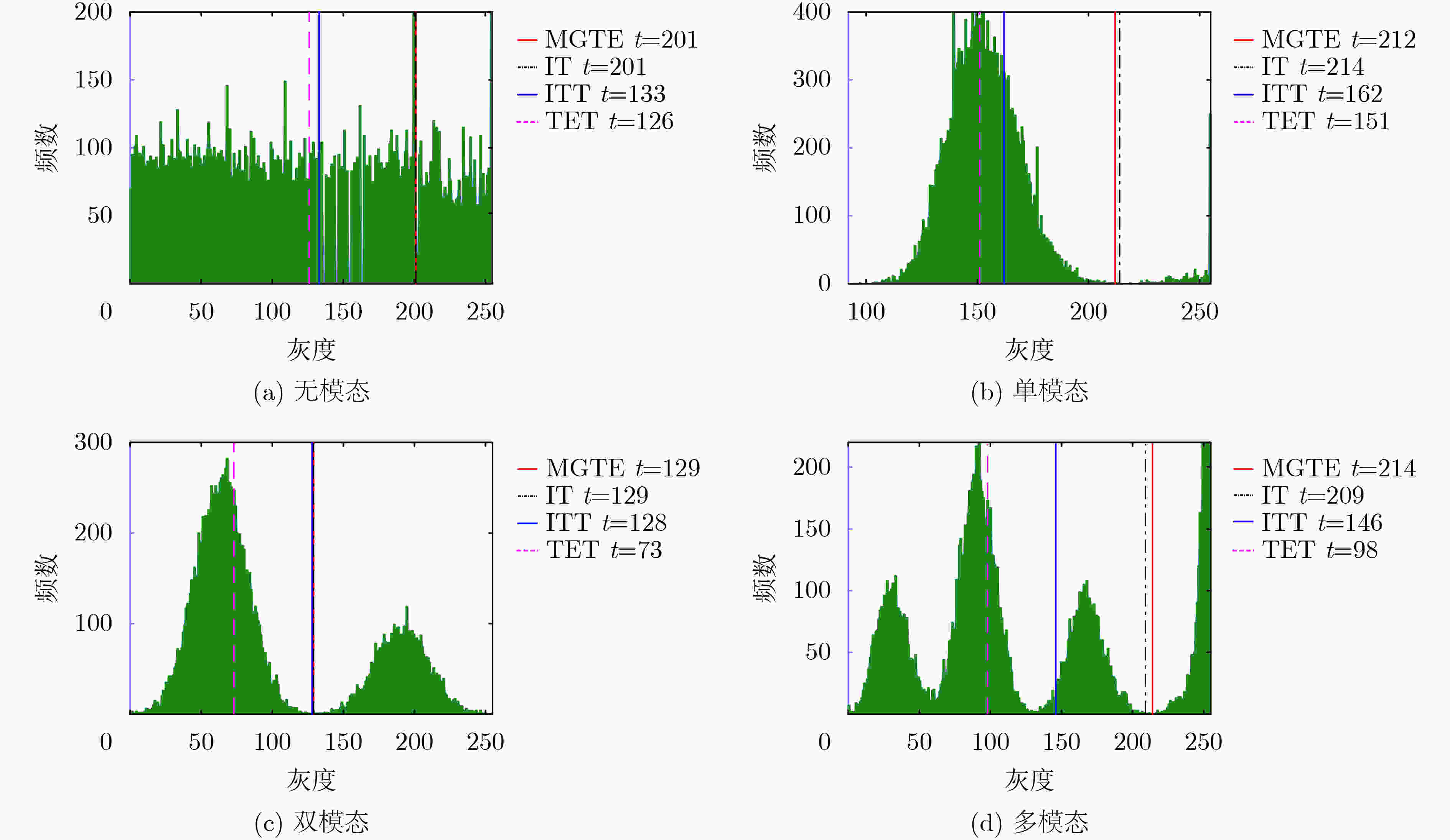
表 1 6个分割方法在4幅合成图像上的分割阈值
t 和ME值(%)分割方法 无模态 单模态 双模态 多模态 t, ME t, ME t, ME t, ME IT 201, 0.00 214, 0.00 129, 0.01 209, 0.00 MGTE 201, 0.00 212, 0.01 129, 0.01 214, 0.01 ITT 133, 22.22 162, 28.80 128, 0.01 146, 17.40 TET 126, 24.00 151, 48.57 73, 21.70 98, 28.16 FRFCM *, 1.17 *, 39.43 *, 0.17 *, 0.87 ICAC *, 19.58 *, 0.02 *, 0.00 *, 2.95 
下载: 导出CSV
表 2 5个分割方法的计算效率比较(s)
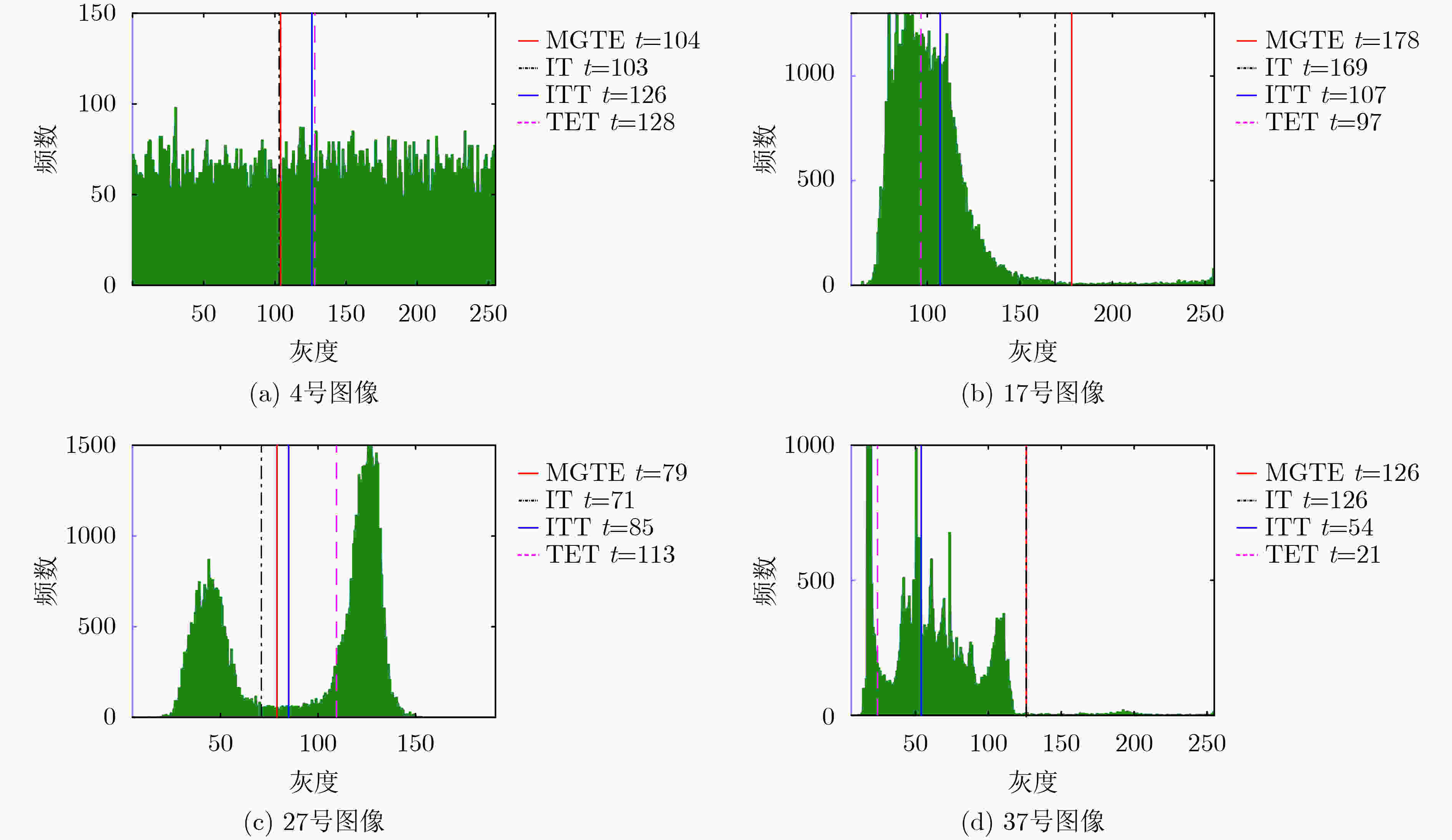
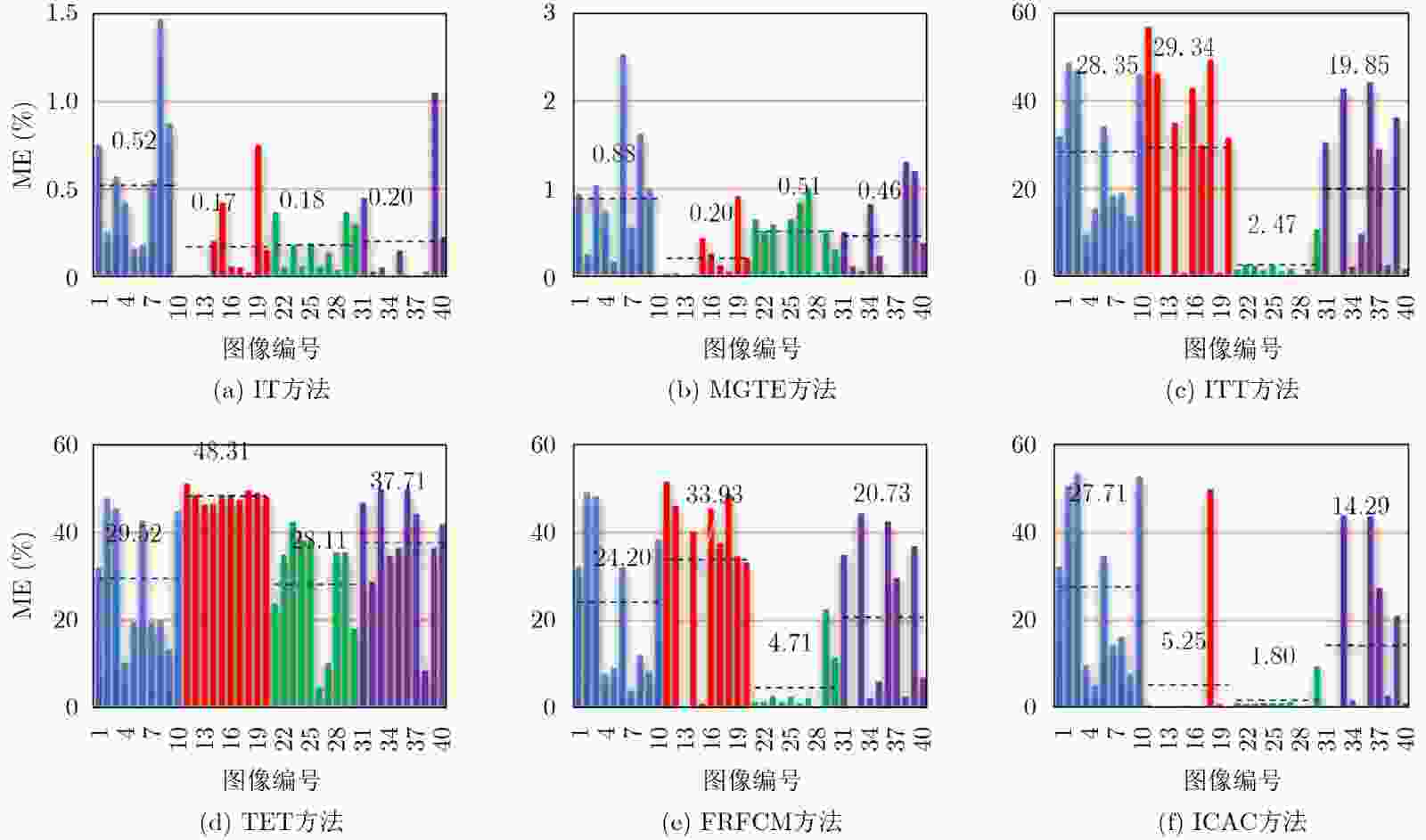
分割方法 合成图像上CPU耗时 真实世界图像上CPU耗时 均值 标准偏差 均值 标准偏差 MGTE 0.453 0.075 0.651 0.312 ITT 0.003 0.002 0.003 0.002 TET 0.010 0.002 0.011 0.003 FRFCM 0.065 0.064 0.030 0.027 ICAC 0.027 0.019 0.194 0.206
下载: 导出CSV
-
[1] 吴一全, 孟天亮, 吴诗婳. 图像阈值分割方法研究进展20年(1994–2014)[J]. 数据采集与处理, 2015, 30(1): 1–23. doi: 10.16337/j.1004-9037.2015.01.001WU Yiquan, MENG Tianliang, and WU Shihua. Research progress of image thresholding methods in recent 20 years (1994–2014)[J]. Journal of Data Acquisition and Processing, 2015, 30(1): 1–23. doi: 10.16337/j.1004-9037.2015.01.001 [2] 范九伦, 雷博. 倒数粗糙熵图像阈值化分割算法[J]. 电子与信息学报, 2020, 42(1): 214–221. doi: 10.11999/JEIT190559FAN Jiulun and LEI Bo. Image thresholding segmentation method based on reciprocal rough entropy[J]. Journal of Electronics &Information Technology, 2020, 42(1): 214–221. doi: 10.11999/JEIT190559 [3] SEZGIN M and SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146–168. doi: 10.1117/1.1631315 [4] KAPUR J N, SAHOO P K, and WONG A K C. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3): 273–285. doi: 10.1016/0734-189X(85)90125-2 [5] 吴一全, 张金矿. 二维直方图θ划分最大Shannon熵图像阈值分割[J]. 物理学报, 2010, 59(8): 5487–5495. doi: 10.7498/aps.59.5487WU Yiquan and ZHANG Jinkuang. Image thresholding based on θ-division of 2-D histogram and maximum Shannon entropy[J]. Acta Physica Sinica, 2010, 59(8): 5487–5495. doi: 10.7498/aps.59.5487 [6] SAHOO P, WILKINS C, and YEAGER J. Threshold selection using Rényi's entropy[J]. Pattern Recognition, 1997, 30(1): 71–84. doi: 10.1016/S0031-3203(96)00065-9 [7] WEI Wei. Gray image thresholding based on three-dimensional Rényi entropy[C]. The 6th International Congress on Image and Signal Processing, Hangzhou, China, 2013: 599–603. [8] 龙建武, 申铉京, 魏巍, 等. 一种结合纹理信息的三维Rényi熵阈值分割算法[J]. 小型微型计算机系统, 2011, 32(5): 948–952.LONG Jianwu, SHEN Xuanjing, WEI Wei, et al. 3-D Rényi entropy thresholding algorithm combining with the texture[J]. Journal of Chinese Computer Systems, 2011, 32(5): 948–952. [9] DE ALBUQUERQUE M P, ESQUEF I A, MELLO A R G, et al. Image thresholding using Tsallis entropy[J]. Pattern Recognition Letters, 2004, 25(9): 1059–1065. doi: 10.1016/j.patrec.2004.03.003 [10] 吴一全, 张金矿. 二维直方图θ-划分Tsallis熵阈值分割算法[J]. 信号处理, 2010, 26(8): 1162–1168. doi: 10.3969/j.issn.1003-0530.2010.08.008WU Yiquan and ZHANG Jinkuang. Image thresholding based on 2-D histogram θ-division and Tsallis entropy[J]. Signal Processing, 2010, 26(8): 1162–1168. doi: 10.3969/j.issn.1003-0530.2010.08.008 [11] YE Zhiwei, YANG Juan, WANG Mingwei, et al. 2D Tsallis entropy for image segmentation based on modified chaotic bat algorithm[J]. Entropy, 2018, 20(4): 239. doi: 10.3390/e20040239 [12] ZHANG Hong. One-dimensional Arimoto entropy threshold segmentation method based on parameters optimization[C]. 2011 International Conference on Applied Informatics and Communication, Xi’an, China, 2011: 573–581. [13] 卓问, 曹治国, 肖阳. 基于二维Arimoto熵的阈值分割方法[J]. 模式识别与人工智能, 2009, 22(2): 208–213. doi: 10.3969/j.issn.1003-6059.2009.02.007ZHUO Wen, CAO Zhiguo, and XIAO Yang. Image thresholding based on two-dimensional Arimoto entropy[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(2): 208–213. doi: 10.3969/j.issn.1003-6059.2009.02.007 [14] NIE Fangyan, ZHANG Pingfeng, LI Jianqi, et al. A novel generalized entropy and its application in image thresholding[J]. Signal Processing, 2017, 134: 23–34. doi: 10.1016/j.sigpro.2016.11.004 [15] SPARAVIGNA A C. Bi-level image thresholding obtained by means of Kaniadakis entropy[EB/OL]. https://arxiv.org/vc/arxiv/papers/1502/1502.04500v2.pdf, 2021. [16] LI C H and LEE C K. Minimum cross entropy thresholding[J]. Pattern Recognition, 1993, 26(4): 617–625. doi: 10.1016/0031-3203(93)90115-D [17] AL-OSAIMI G and EL-ZAART A. Minimum cross entropy thresholding for SAR images[C]. The 3rd International Conference on Information and Communication Technologies: From Theory to Applications, Damascus, Syria, 2008: 1245–1250. [18] ZHU Zhenfeng, LU Hanqing, and ZHAO Yao. Scale multiplication in odd Gabor transform domain for edge detection[J]. Journal of Visual Communication and Image Representation, 2007, 18(1): 68–80. doi: 10.1016/j.jvcir.2006.10.001 [19] LINDEBERG T. Scale-space for discrete signals[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(3): 234–254. doi: 10.1109/34.49051 [20] SUYARI H and TSUKADA M. Law of error in Tsallis statistics[J]. IEEE Transactions on Information Theory, 2005, 51(2): 753–757. doi: 10.1109/TIT.2004.840862 [21] 闫海霞, 赵晓晖. 基于Tsallis熵差的遥感图像边缘检测方法[J]. 计算机应用研究, 2009, 26(9): 3598–3600. doi: 10.3969/j.issn.1001-3695.2009.09.117YAN Haixia and ZHAO Xiaohui. Edge detection method based on Tsallis entropy difference of remote sensing image[J]. Application Research of Computers, 2009, 26(9): 3598–3600. doi: 10.3969/j.issn.1001-3695.2009.09.117 [22] TSALLIS C. Possible generalization of Boltzmann-Gibbs statistics[J]. Journal of Statistical Physics, 1988, 52(1/2): 479–487. doi: 10.1007/BF01016429 [23] BEMIS R. Thresholding tool[EB/OL]. http://cn.mathworks.com/matlabcentral/fileexchange/6770-thresholding-tool, 2022. [24] CAI Hongmin, YANG Zhong, CAO Xinhua, et al. A new iterative triclass thresholding technique in image segmentation[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1038–1046. doi: 10.1109/TIP.2014.2298981 [25] LEI Tao, JIA Xiaohong, ZHANG Yanning, et al. Significantly fast and robust fuzzy C-means clustering algorithm based on morphological reconstruction and membership filtering[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 3027–3041. doi: 10.1109/TFUZZ.2018.2796074 [26] WANG Dong and WANG Xiaoping. The Iterative Convolution-Thresholding Method (ICTM) for image segmentation[EB/OL]. https://arxiv.org/pdf/1904.10917.pdf, 2021. 期刊类型引用(5)
1. 栗晓政，崔凤庆，宋晓燕，梁纲，樊彦国，邱震辉，杨庆. 基于MEMS传感器的线路电压测量方法研究. 工业仪表与自动化装置. 2024(03): 123-127 . 
百度学术2. 李子博，陈小龙，欧阳吉庭，缪劲松，张宇，王若珏，高志良. 静电电位非接触式测量的偏差和修正. 测试技术学报. 2024(06): 618-626 . 百度学术3. 雷虎成，夏善红，彭春荣，毋正伟，张洲威，刘俊，彭思敏，刘向明，高雅浩. 基于锆钛酸铅的低电压驱动MEMS电场传感器研究. 电子与信息学报. 2023(01): 150-157 . 
本站查看4. 储昭志，杨鹏飞，闻小龙，彭春荣，刘宇涛，吴双. 一种灵敏度漂移自补偿型MEMS电场传感器. 电子与信息学报. 2023(08): 3040-3046 . 本站查看5. 张广洲，方书博，张振宇，冯智慧，韩晴. 基于振动传感的直流合成电场测量结构设计. 中国电力. 2023(11): 151-159 . 百度学术其他类型引用(2)
-
下载:
百度学术
计量
- 文章访问数: 790
- HTML全文浏览量: 411
- PDF下载量: 102
- 被引次数: 7
下载:
