基于空间特征的生成对抗网络数据生成方法

孙磊; 杨宇; 毛秀青; 汪小芹; 李佳欣

doi:10.11999/JEIT211285

基于空间特征的生成对抗网络数据生成方法

doi: 10.11999/JEIT211285

战略支援部队信息工程大学郑州 450001

详细信息

作者简介:
孙磊：男，教授，研究方向为密码与系统安全、机器学习安全

杨宇：女，硕士生，研究方向为计算机视觉、生成对抗网络

毛秀青：男，副教授，研究方向为智能信息系统安全

汪小芹：女，硕士生，研究方向为计算机视觉

通讯作者:
杨宇　yuyoung0107@163.com

中图分类号: TP183;TN03
计量
- 文章访问数: 929
- HTML全文浏览量: 706
- PDF下载量: 216
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-17
- 修回日期: 2022-01-10
- 录用日期: 2022-01-20
- 网络出版日期: 2022-02-03
- 刊出日期: 2023-06-10

Data Generation Based on Generative Adversarial Network with Spatial Features

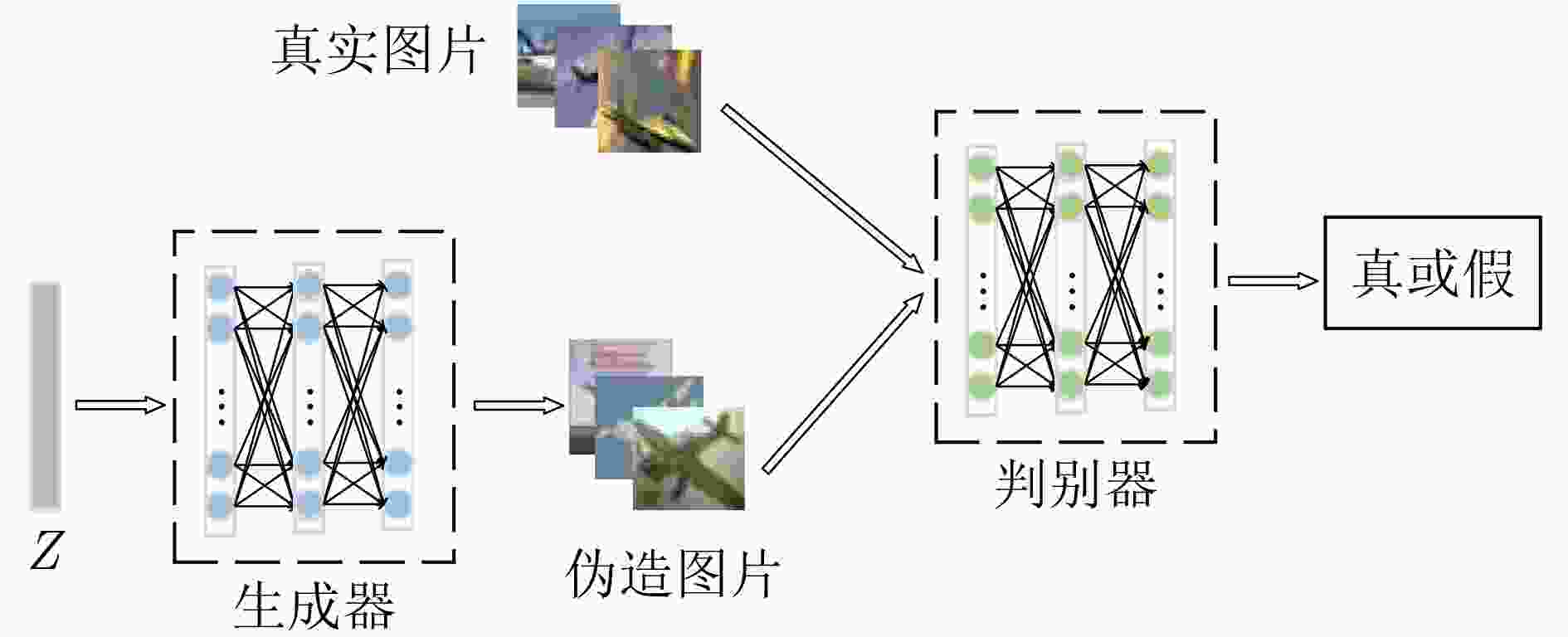
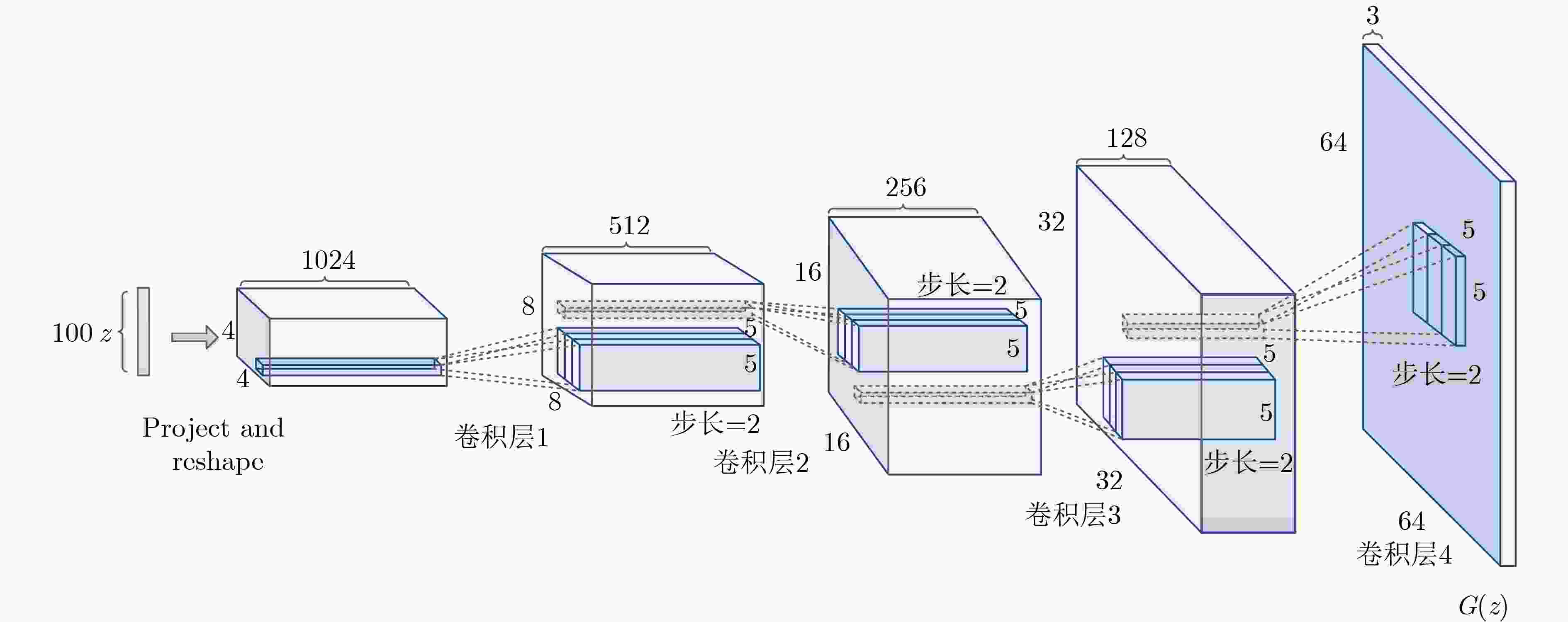
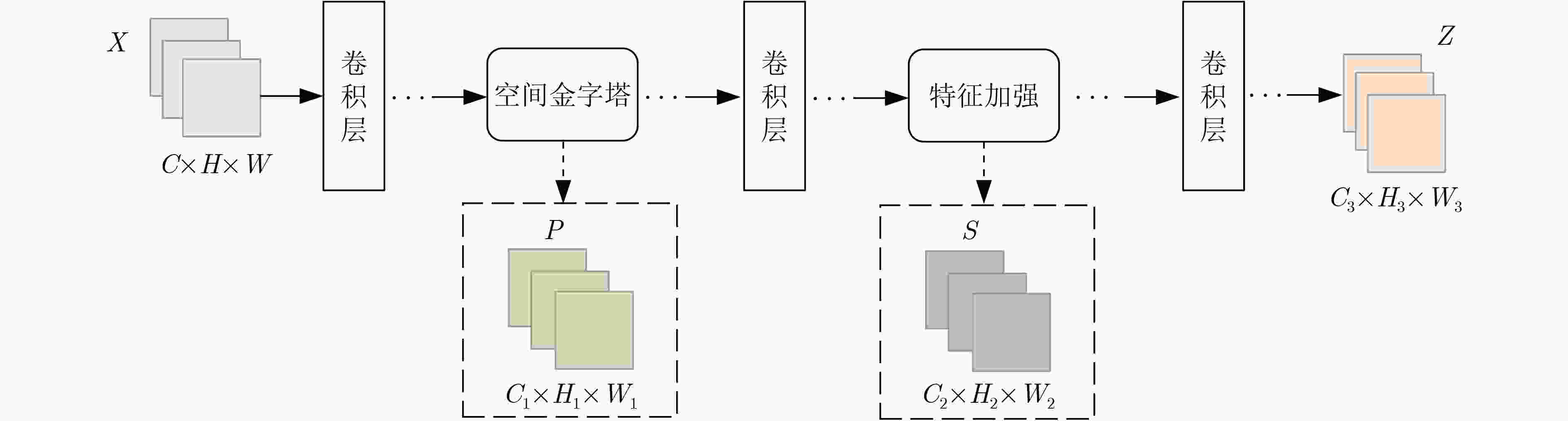
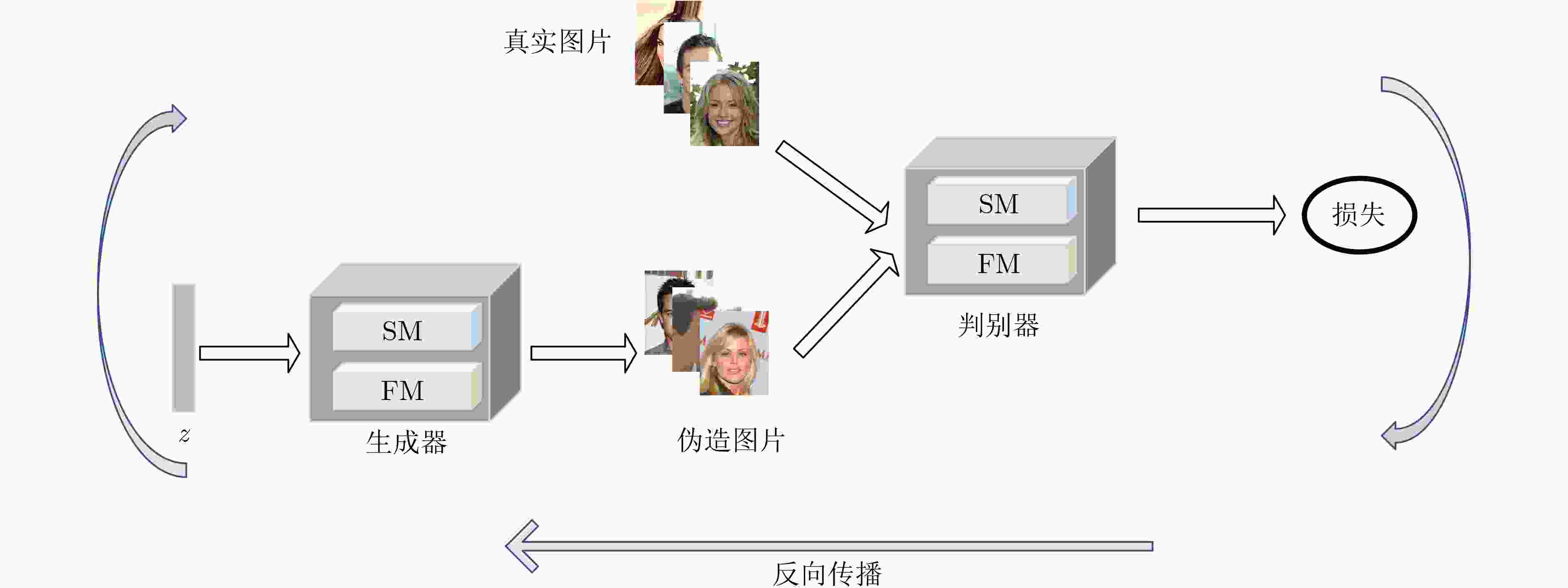
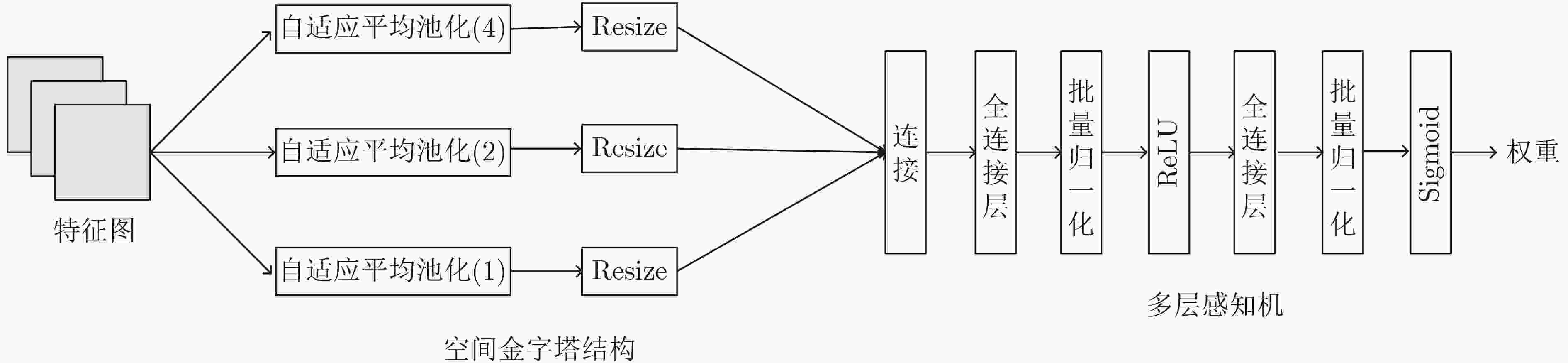
PLA Strategic Support Force Information Engineering University, Zhengzhou 450001, China

摘要

摘要: 传统的生成对抗网络(GAN)在特征图较大的情况下，忽略了原始特征的表示和结构信息，并且生成图像的像素之间缺乏远距离相关性，从而导致生成的图像质量较低。为了进一步提高生成图像的质量，该文提出一种基于空间特征的生成对抗网络数据生成方法(SF-GAN)。该方法首先将空间金字塔网络加入生成器和判别器，来更好地捕捉图像的边缘等重要的描述信息；然后将生成器和判别器进行特征加强，来建模像素之间的远距离相关性。使用CelebA,SVHN,CIFAR-10等小规模数据集进行实验，通过定性和盗梦空间得分(IS)、弗雷歇距离(FID)定量评估证明了所提方法相比梯度惩罚生成对抗网络(WGAN-GP)、自注意力生成对抗网络(SAGAN)能使生成的图像具有更高的质量。并且通过实验证明了该方法生成的数据能够进一步提升分类模型的训练效果。
- 生成对抗网络 /
- 空间金字塔网络 /
- 特征加强 /
- 特征图
Abstract: Traditional Generative Adversarial Network (GAN) ignores the representation and structural information of the original feature when the feature map is large, and there is no remote correlation between the pixels of the generated images, resulting image quality is low. To improve the quality of the generated images further, a method of data generation based on Generative Adversarial Network with Spatial Features (SF-GAN) is proposed. Firstly, the spatial pyramid network is added into the generator and discriminator to capture the important description information better such as the edge of the images. Then the features of the generator and discriminator are strengthened to model the remote correlation between pixels. Experiments are performed with small-scale benchmarks (CelebA, SVHN, and CIFAR-10). Compared with improved training of Wasserstein GANs (WGAN-GP) and Self-Attention Generative Adversarial Networks (SAGAN) by qualitative and quantitative evaluation of Inception Score (IS) and Frechet Inception Distance (FID), the proposed method can generate higher quality images. The experiment proves that the generated images can improve the training effect of the classified model further.
- Generative Adversarial Network (GAN) /
- Spatial pyramid network /
- Feature strengthen /
- Feature maps

HTML全文

图 1 GAN结构示意图

下载: 全尺寸图片幻灯片

图 2 DCGAN生成器结构示意图

下载: 全尺寸图片幻灯片

图 3 SF-GAN的模型框架

下载: 全尺寸图片幻灯片

图 4 SF-GAN的网络训练流程图

下载: 全尺寸图片幻灯片

图 5 空间金字塔结构

下载: 全尺寸图片幻灯片

图 6 不同模型生成样本对比

下载: 全尺寸图片幻灯片

图 7 不同模型在CelebA数据集上的生成效果

下载: 全尺寸图片幻灯片

图 8 不同模型在数字8上的生成效果

下载: 全尺寸图片幻灯片

图 9 不同模型在CIFAR-10上的生成效果

下载: 全尺寸图片幻灯片

图 10 SVHN增强后训练集损失的变化

下载: 全尺寸图片幻灯片

图 11 SVHN增强后训练集和测试集分类准确率

下载: 全尺寸图片幻灯片

图 12 CIFAR-10增强后训练集损失的变化

下载: 全尺寸图片幻灯片

图 13 CIFAR-10增强后训练集和测试集分类准确率

下载: 全尺寸图片幻灯片

表 1 在CelebA数据集上不同模型的对比结果

模型	IS↑	FID↓
WGAN-GP	2.189	55.324
SAGAN	2.238	47.624
SF-GAN	2.468	47.064

下载: 导出CSV

表 2 在SVHN数据集上不同模型的IS对比结果

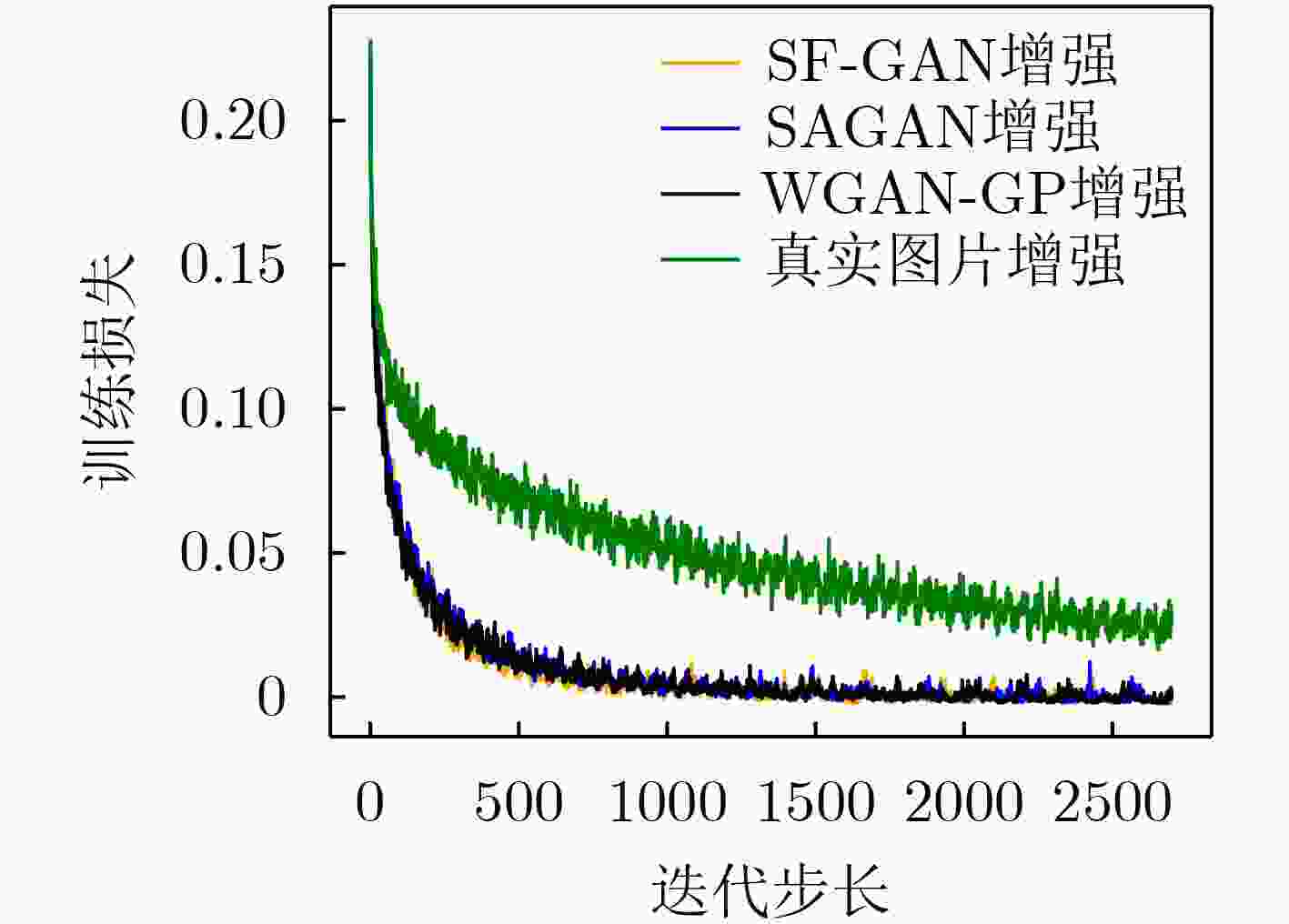
模型	0	1	2	3	4	5	6	7	8	9
WGAN-GP	2.653	2.223	2.484	2.507	2.328	2.507	2.709	2.423	2.810	2.689
SAGAN	2.603	2.291	2.514	2.446	2.460	2.493	2.599	2.559	2.681	2.704
SF-GAN	2.967	2.584	2.893	2.826	2.683	2.803	2.970	2.916	3.063	3.005

下载: 导出CSV

表 3 在SVHN数据集上不同模型的FID对比结果

模型	0	1	2	3	4	5	6	7	8	9
WGAN-GP	106.800	101.017	89.446	100.502	96.387	96.058	101.426	124.202	111.576	129.814
SAGAN	113.999	95.865	101.994	98.829	87.574	99.081	109.677	103.439	111.394	108.792
SF-GAN	82.167	74.754	77.222	75.660	75.008	71.066	72.051	82.132	80.748	83.660

下载: 导出CSV

表 4 在CIFAR-10数据集上不同模型的IS对比结果

模型	飞机	汽车	鸟	猫	鹿	狗	蛙	马	轮船	卡车
WGAN-GP	3.738	3.156	3.018	2.990	2.491	3.354	2.496	3.426	3.206	2.853
SAGAN	3.756	3.273	3.042	2.971	2.627	3.523	2.506	3.619	3.073	3.099
SF-GAN	4.090	3.803	3.551	3.295	3.038	4.176	2.912	3.820	3.495	3.281

下载: 导出CSV

表 5 在CIFAR-10数据集上不同模型的FID对比结果

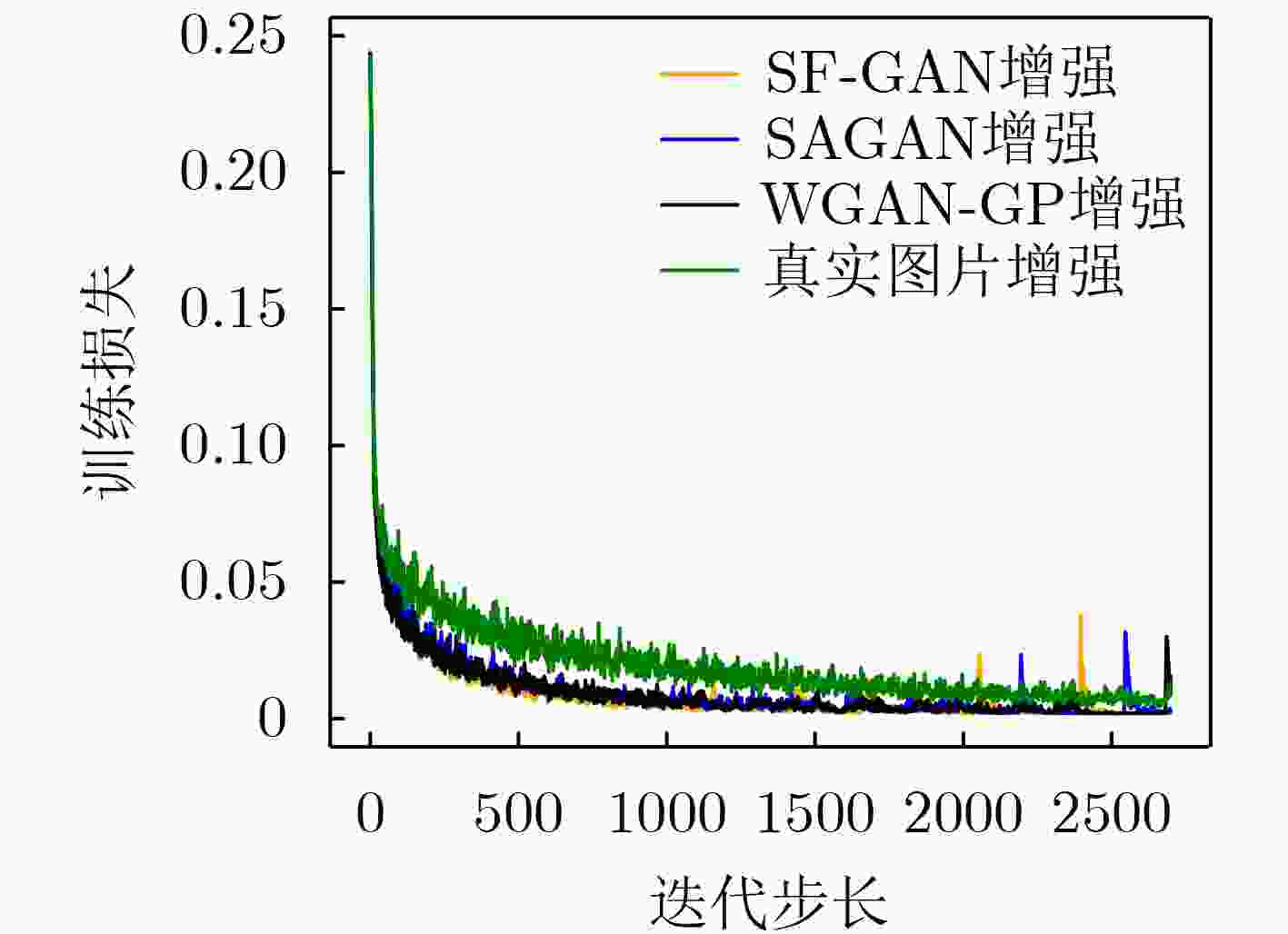
模型	飞机	汽车	鸟	猫	鹿	狗	蛙	马	轮船	卡车
WGAN-GP	150.220	117.988	138.229	135.831	107.385	125.356	109.235	104.255	101.760	110.521
SAGAN	144.611	164.207	131.030	162.071	102.087	134.925	106.684	112.162	120.274	150.129
SF-GAN	124.756	144.981	107.929	128.807	81.551	106.698	87.428	95.52	92.263	108.855

下载: 导出CSV

表 6 不同方法增强后SVHN测试集的分类准确率(%)

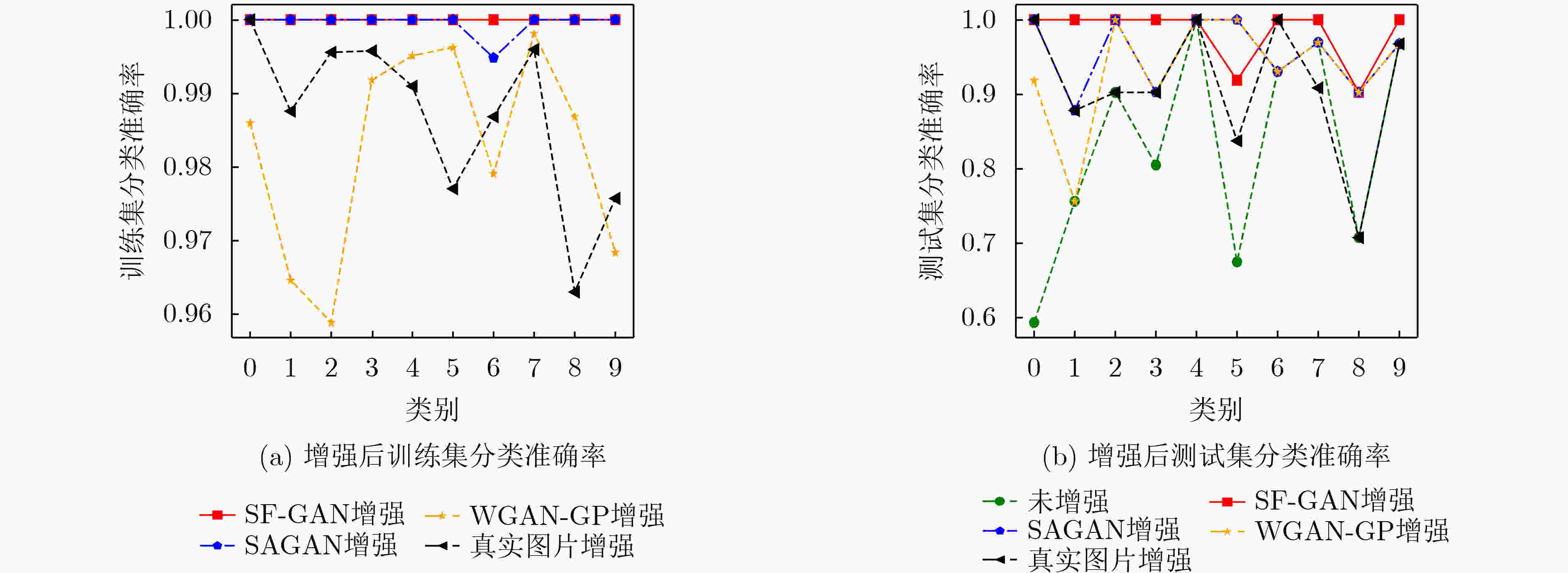
模型	0	1	2	3	4	5	6	7	8	9	平均准确率
未增强	58.33	75.00	90.00	80.00	100.00	66.67	92.86	96.88	70.00	96.67	87.65
真实图片增强	100.00	87.50	90.00	90.00	100.00	83.33	100.00	90.62	70.00	96.67	90.51
WGAN-GP 增强	91.67	75.00	100.00	90.00	87.50	100.00	96.43	96.88	80.00	93.33	92.39
SAGAN增强	100.00	87.50	100.00	90.00	100.00	100.00	92.86	96.88	90.00	96.67	95.29
SF-GAN增强	100.00	100.00	100.00	100.00	100.00	91.67	100.00	100.00	90.00	100.00	98.31

下载: 导出CSV

表 7 不同方法增强后CIFAR-10测试集的分类准确率(%)

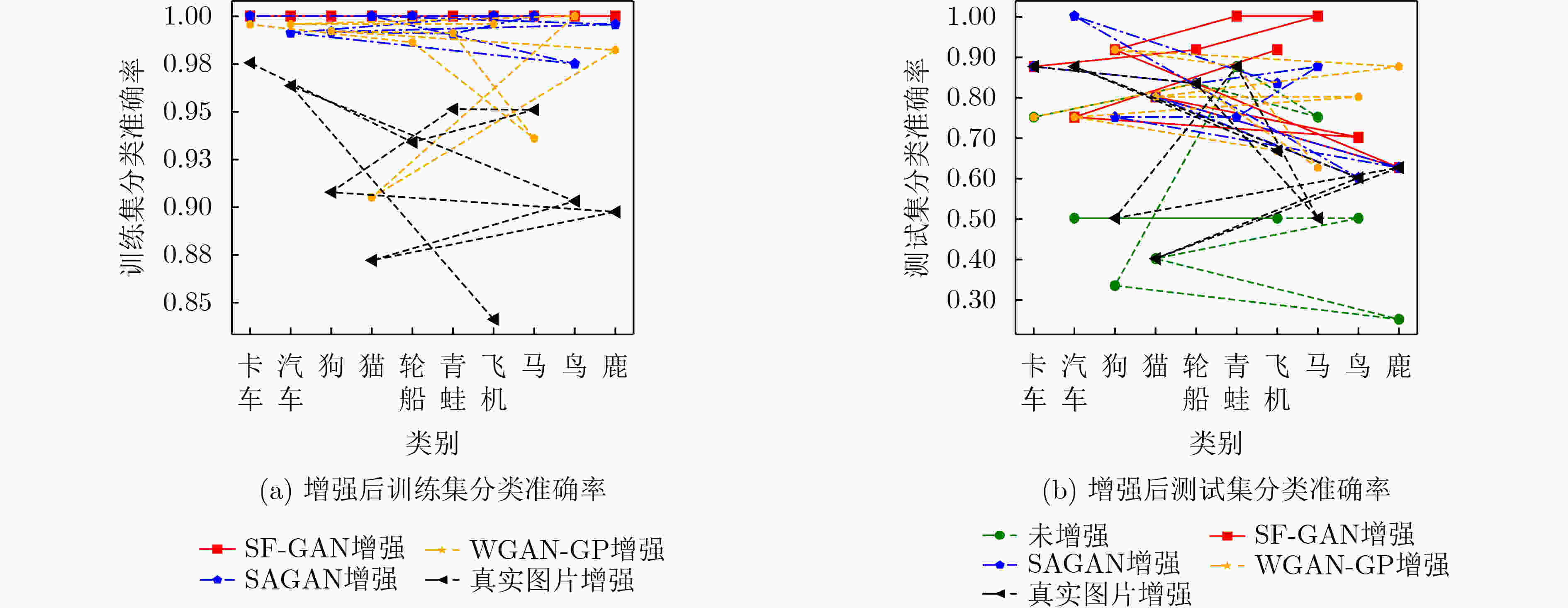
模型	飞机	汽车	鸟	猫	鹿	狗	蛙	马	轮船	卡车	平均准确率
未增强	50.00	50.50	50.00	40.00	25.00	33.33	87.50	75.00	83.33	75.00	52.47
真实图片增强	66.67	87.50	60.00	40.00	62.50	50.00	87.50	50.00	83.33	87.50	66.67
WGAN-GP 增强	66.67	75.00	80.00	80.00	87.50	91.67	87.50	62.50	83.33	75.00	76.87
SAGAN增强	83.33	100.00	60.00	80.00	62.50	75.00	75.00	87.50	83.33	87.50	78.47
SF-GAN增强	91.67	75.00	70.00	80.00	62.50	91.67	100.00	100.00	91.67	87.50	86.33

下载: 导出CSV

参考文献(29)

[1]	TAN Mingxing and LE Q V. EfficientNetV2: Smaller models and faster training[C]. The 38th International Conference on Machine Learning, San Diego, USA, 2021: 10096–10106.
[2]	XIAO Zihao, GAO Xianfeng, FU Chilin, et al. Improving transferability of adversarial patches on face recognition with generative models[C]. 2021 IEEE/CVF Conference on Computer vision and Pattern Recognition, Nashville, USA, 2021: 11840–11849.
[3]	CHEN Xiangning, XIE Cihang, TAN Mingxing, et al. Robust and accurate object detection via adversarial learning[C]. 2021 IEEE/CVF Computer vision and Pattern Recognition, Nashville, USA, 2021: 16617–16626.
[4]	CHEN Pinchun, KUNG B H, and CHEN Juncheng. Class-aware robust adversarial training for object detection[C]. 2021 IEEE/CVF Conference on Computer vision and Pattern Recognition, Nashville, USA, 2021: 10415–10424.
[5]	张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机[J]. 工程数学学报, 2015, 32(2): 159–173. doi: 10.3969/j.issn.1005-3085.2015.02.001 ZHANG Chunxia, JI Nannan, and WANG Guanwei. Restricted Boltzmann machines[J]. Chinese Journal of Engineering Mathematics, 2015, 32(2): 159–173. doi: 10.3969/j.issn.1005-3085.2015.02.001
[6]	LOPES N and RIBEIRO B. Deep belief networks (DBNs)[M]. LOPES N and RIBEIRO B. Machine Learning for Adaptive Many-Core Machines - A Practical Approach. Cham: Springer, 2015: 155–186.
[7]	KINGMA D P and WELLING M. Auto-encoding variational Bayes[C]. The 2nd International Conference on Learning Representations, Banff, Canada, 2014.
[8]	GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672–2680.
[9]	LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791
[10]	RADFORD A, METZ L, and CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[C]. The 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016.
[11]	ARJOVSKY M, CHINTALA S, and BOTTOU L. Wasserstein generative adversarial networks[C]. The 34th International Conference on Machine Learning, Sydney, Australia, 2017: 214–223.
[12]	BLEI D M, KUCUKELBIR A, and MCAULIFFE J D. Variational inference: A review for statisticians[J]. Journal of the American statistical Association, 2017, 112(518): 859–877. doi: 10.1080/01621459.2017.1285773
[13]	WEAVER N. Lipschitz Algebras[M]. Singapore: World Scientific, 1999.
[14]	GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of wasserstein GANs[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 5769–5779.
[15]	ZHANG Han, GOODFELLOW I, METAXAS D, et al. Self-attention generative adversarial networks[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019.
[16]	GUO Jingda, MA Xu, SANSOM A, et al. Spanet: Spatial pyramid attention network for enhanced image recognition[C]. 2020 IEEE International Conference on Multimedia and Expo, London, UK, 2020: 1–6.
[17]	丁斌, 夏雪, 梁雪峰. 基于深度生成对抗网络的海杂波数据增强方法[J]. 电子与信息学报, 2021, 43(7): 1985–1991. doi: 10.11999/JEIT200447 DING Bin, XIA Xue, and LIANG Xuefeng. Sea clutter data augmentation method based on deep generative adversarial network[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1985–1991. doi: 10.11999/JEIT200447
[18]	曹志义, 牛少彰, 张继威. 基于半监督学习生成对抗网络的人脸还原算法研究[J]. 电子与信息学报, 2018, 40(2): 323–330. doi: 10.11999/JEIT170357 CAO Zhiyi, NIU Shaozhang, and ZHANG Jiwei. Research on face reduction algorithm based on generative adversarial nets with semi-supervised learning[J]. Journal of Electronics &Information Technology, 2018, 40(2): 323–330. doi: 10.11999/JEIT170357
[19]	ZEILER M D, KRISHNAN D, TAYLOR G W, et al. Deconvolutional networks[C]. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, USA, 2010: 2528–2535.
[20]	IOFFE S and SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. The 32nd International Conference on International Conference on Machine Learning, Lille, France, 2015: 448–456.
[21]	DAHL G E, SAINATH T N, and HINTON G E. Improving deep neural networks for LVCSR using rectified linear units and dropout[C]. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013: 8609–8613.
[22]	XIAO F, HONMA Y, and KONO T. A simple algebraic interface capturing scheme using hyperbolic tangent function[J]. International Journal for Numerical Methods in Fluids, 2005, 48(9): 1023–1040. doi: 10.1002/fld.975
[23]	XU Bing, WANG Naiyan, CHEN Tianqi, et al. Empirical evaluation of rectified activations in convolutional network[J]. arXiv preprint arXiv: 1505.00853, 2015.
[24]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778.
[25]	LIU Ziwei, LUO Ping, WANG Xiaogang, et al. Large-scale CelebFaces attributes (CelebA) dataset[Z]. Retrieved August, 2018.
[26]	KRIZHEVSKY A. Learning multiple layers of features from tiny images[D]. [Master dissertation], University of Toronto, 2009.
[27]	SALIMANS T, GOODFELLOW I, ZAREMBA W, et al. Improved techniques for training GANs[C]. The 30th Conference on Neural Information Processing Systems, Barcelona, Spain, 2016: 2234–2242.
[28]	DOWSON D C and LANDAU B V. The Fréchet distance between multivariate normal distributions[J]. Journal of Multivariate Analysis, 1982, 12(3): 450–455. doi: 10.1016/0047-259X(82)90077-X
[29]	KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015.