Massive MIMO Signal Detection Based on Interference Cancellation Assisted Sparsely Connected Neural Network
-
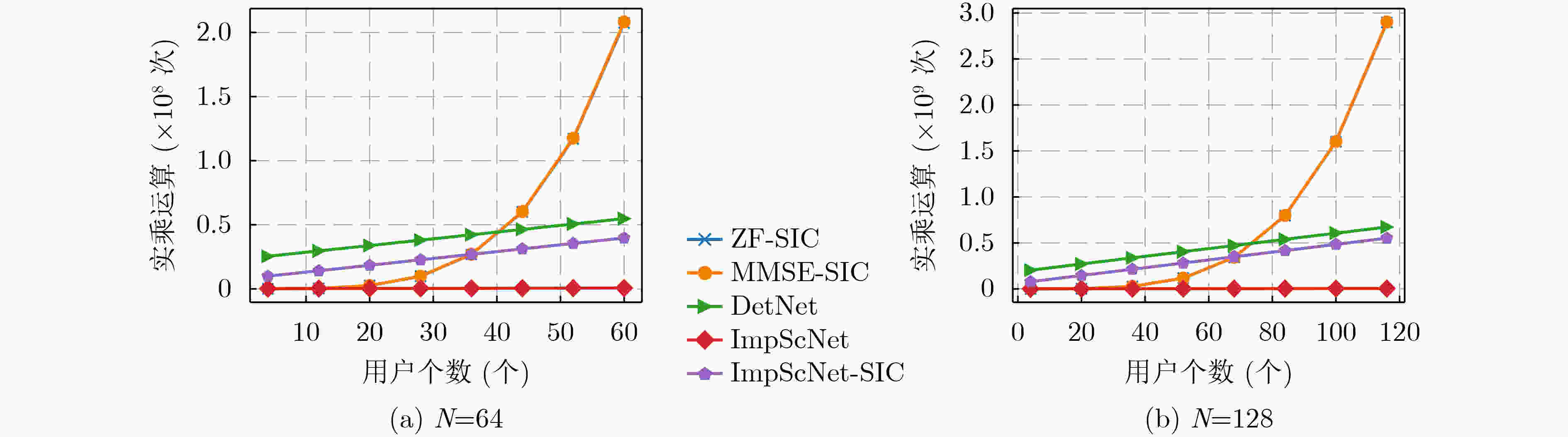
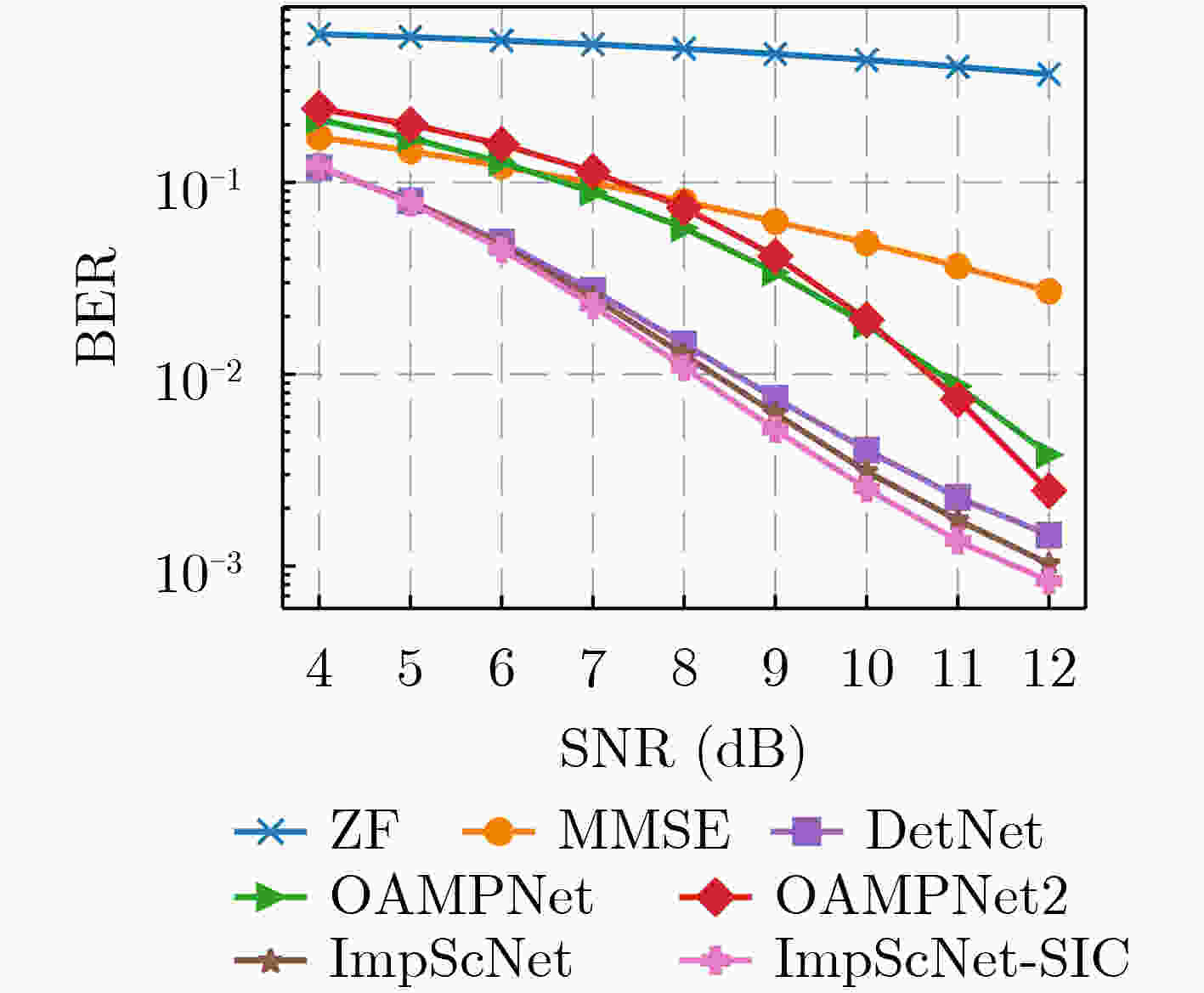
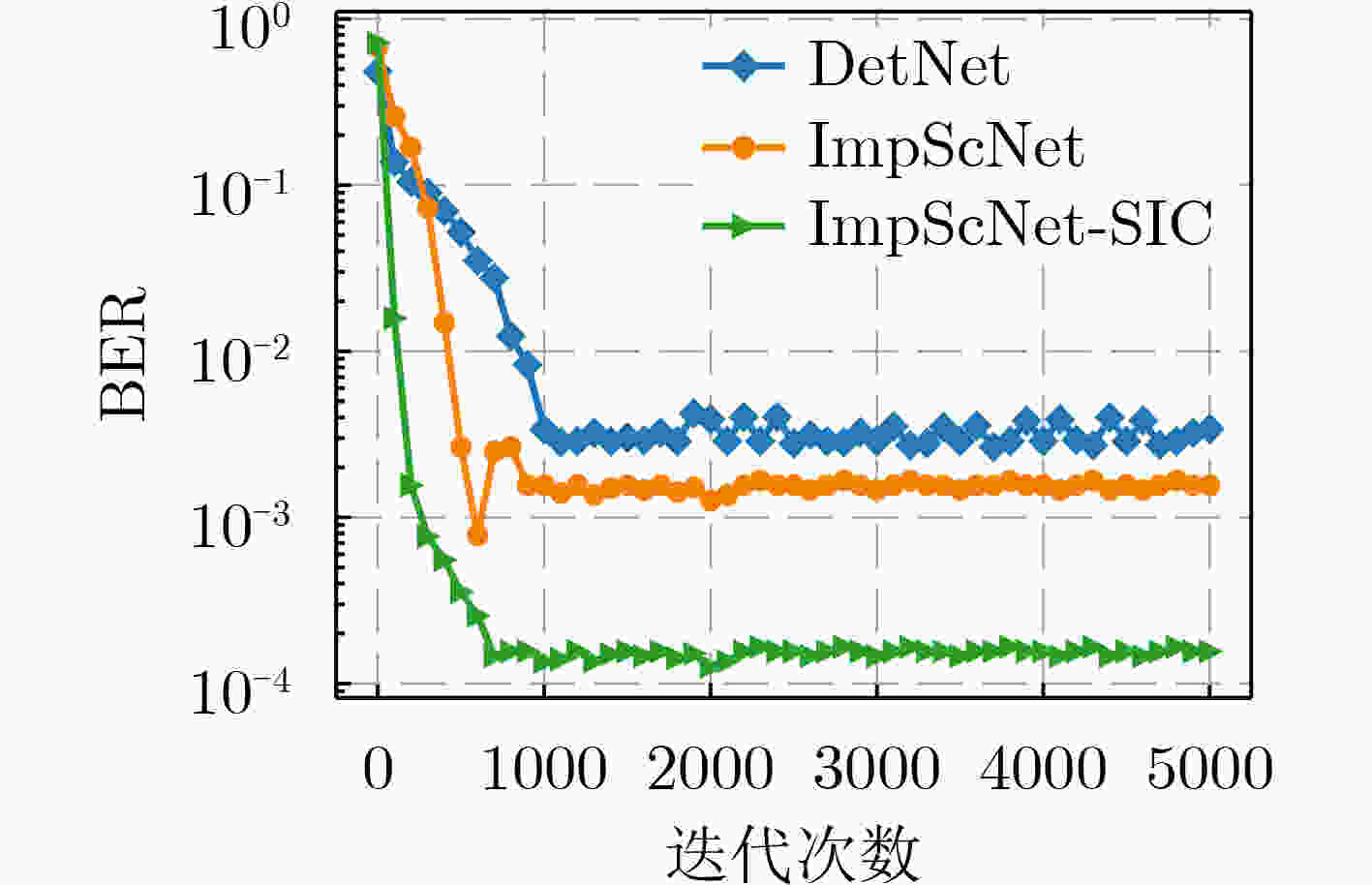
摘要: 近年来,深度学习成为无线通信领域的关键技术之一。在基于深度学习的一系列MIMO信号检测算法中,大多未充分考虑相邻天线之间的干扰消除问题,无法彻底消除多用户干扰对误码率性能的影响。为此,该文提出一种将深度学习与串行干扰消除(SIC)算法进行结合的方法用于大规模MIMO系统上行链路信号检测。首先,通过优化传统的检测网络(DetNet)及改进ScNet检测算法,该文提出一种基于深度神经网络(DNN)的检测算法,称为ImpScNet。在此基础上,进一步将SIC思想应用到深度学习框架结构设计中,提出一种基于深度学习的大规模MIMO多用户SIC检测算法,称为ImpScNet-SIC。此算法在每个检测层上分为两级,其中,第1级由该文提出的ImpScNet算法提供初始解,再将初始解解调至相应的星座点上作为SIC的输入,由此构成该算法的第2级。此外,在SIC中也使用了ImpScNet算法估计传输符号,以便获得最优性能。仿真结果表明,与已有的各种典型代表算法相比,该文所提ImpScNet-SIC检测算法特别适合大规模MIMO信号检测,具有收敛速度快、收敛稳定及复杂度相对较低的优势,并且在10–3误码率上有至少0.5 dB以上的增益。Abstract: In recent years, deep learning has become one of the key technologies in the field of wireless communication. In a series of MIMO signal detection algorithms based on deep learning, most of them do not fully consider the interference cancellation problem between adjacent antennas, hence the impact of multi-user interference on the bit error rate performance can not be completely eliminated. To this end, a method that combines deep learning and Successive Interference Cancellation (SIC) algorithms for uplink signal detection in a massive MIMO system is propesed. Firstly, by optimizing the traditional Detection Network (DetNet) and improving the ScNet (Sparsely connected neural Network), a detection algorithm based on the Deep Neural Network (DNN), called Improved ScNet (ImpScNet), is proposed. On this basis, the SIC is applied to the design of the deep learning framework structure, and a massive MIMO multi-user SIC detection algorithm based on deep learning is proposed, which is called ImpScNet-SIC. This algorithm is divided into two stages on each detection layer. The first stage is provided by the ImpScNet algorithm proposed in this paper to provide the initial solution, and then the initial solution is demodulated to the corresponding constellation point as the input of the SIC, which constitutes the second stage. In addition, the ImpScNet algorithm is also used in SIC to estimate the transmitted symbols in order to obtain the best performance. Simulation results show that, compared with various typical representative algorithms, the ImpScNet-SIC detection algorithm proposed in this paper is particularly suitable for the massive MIMO signal detection. It has the advantages of fast convergence speed, stable convergence and relatively low complexity. And there is at least 0.5 dB gain in 10–3 bit error rate.
-
表 1 MIMO信号检测算法对比
算法分类 算法名称 对比总结 传统检测算法 线性检测算法 MF[20], ZF[7], MMSE[8] (1) ML性能最优,但复杂度呈指数级上升;(2) SD性能次优,是以牺牲复杂度为代价;(3) 其他算法复杂度较低,但性能有待提高 非线性检测算法 ML[3],干扰消除算法[5, 6],SD[4] 基于深度学习
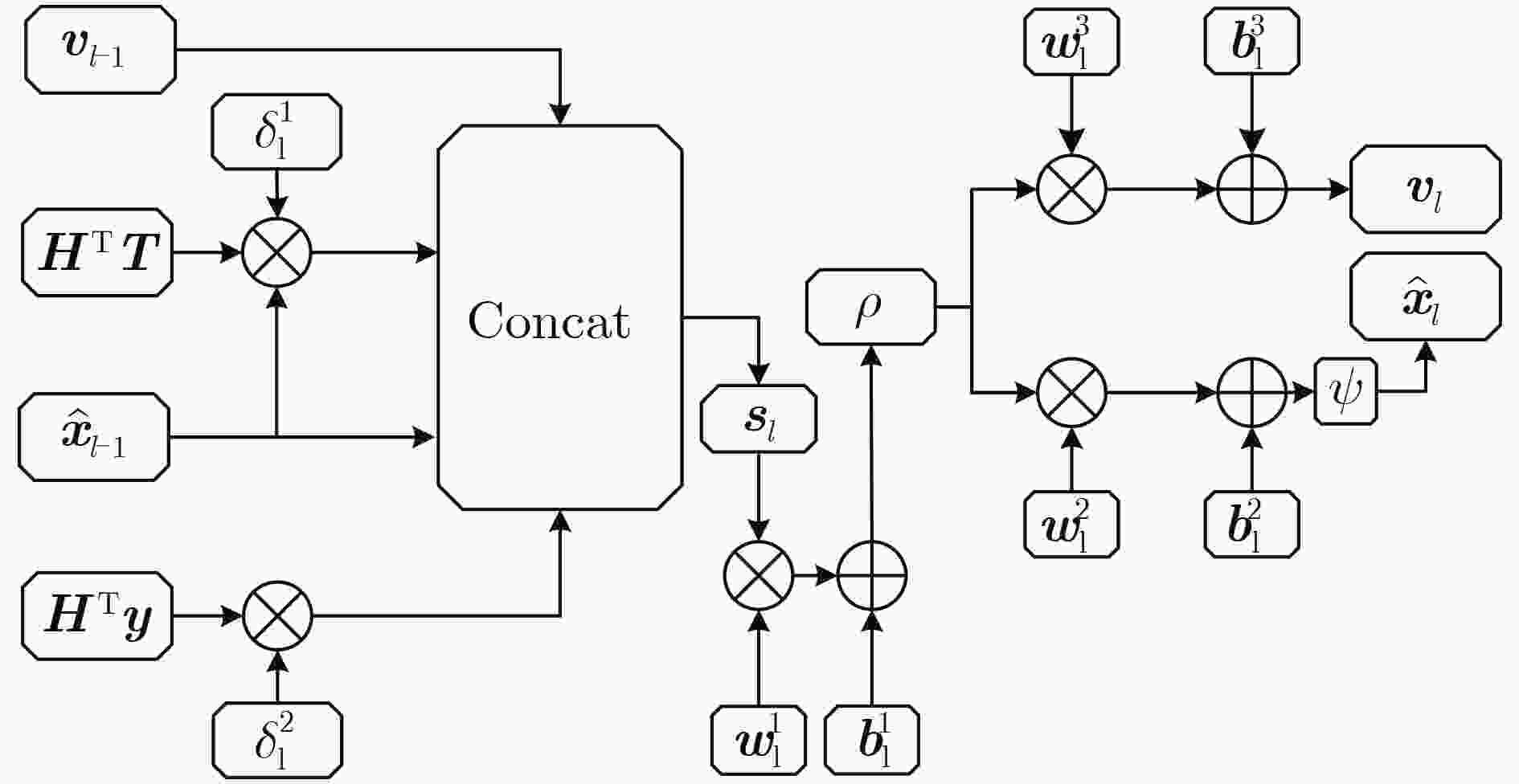
检测算法学习类算法 DetNet[17], ScNet[19], LISA[13] (1) DetNet对天线数量有严格要求,复杂度偏高;(2) ScNet受网络稀疏性影响,仅在大规模才表现出较好的性能;(3) LISA仅适用于常规的MIMO信号检测 消息传递类算法 OAMPNet[14], DNN-dBP[16], DNN-MS[16] (1) OAMPNet可调参数少,容易训练,但需假设信道矩阵是酉不变矩阵;(2) DNN-dBP和DNN-MS涉及可调参数较多,复杂度偏高 可训练类算法 TPG[21], TAMP[22] (1) TPG主要针对下行链路过载信道;(2) TAMP采用全连接作预处理,可调参数多,复杂度偏高 算法1 ImpScNet-SIC检测算法训练流程 输入:${\boldsymbol{x}}$, ${\boldsymbol{y}}$, ${\boldsymbol{H}}$, $L$, $\alpha $, $\beta $, $t$ 输出:${{\stackrel\smile{x} } }_l$ (1) 初始化:${ { {\hat {\boldsymbol x} } }_0}{\text{ = } }{{ {\textit{0}}} }$,$L = 15$,$\alpha = 0.2$,$\beta = 0.5$,$t = 0.1$ (2) 输入各项参数,训练:$ {\boldsymbol{\theta }} = \left\{ {{{\boldsymbol{w}}_l},{{\boldsymbol{b}}_l}} \right\}_{l = 1}^L $ ,使得损失函数最
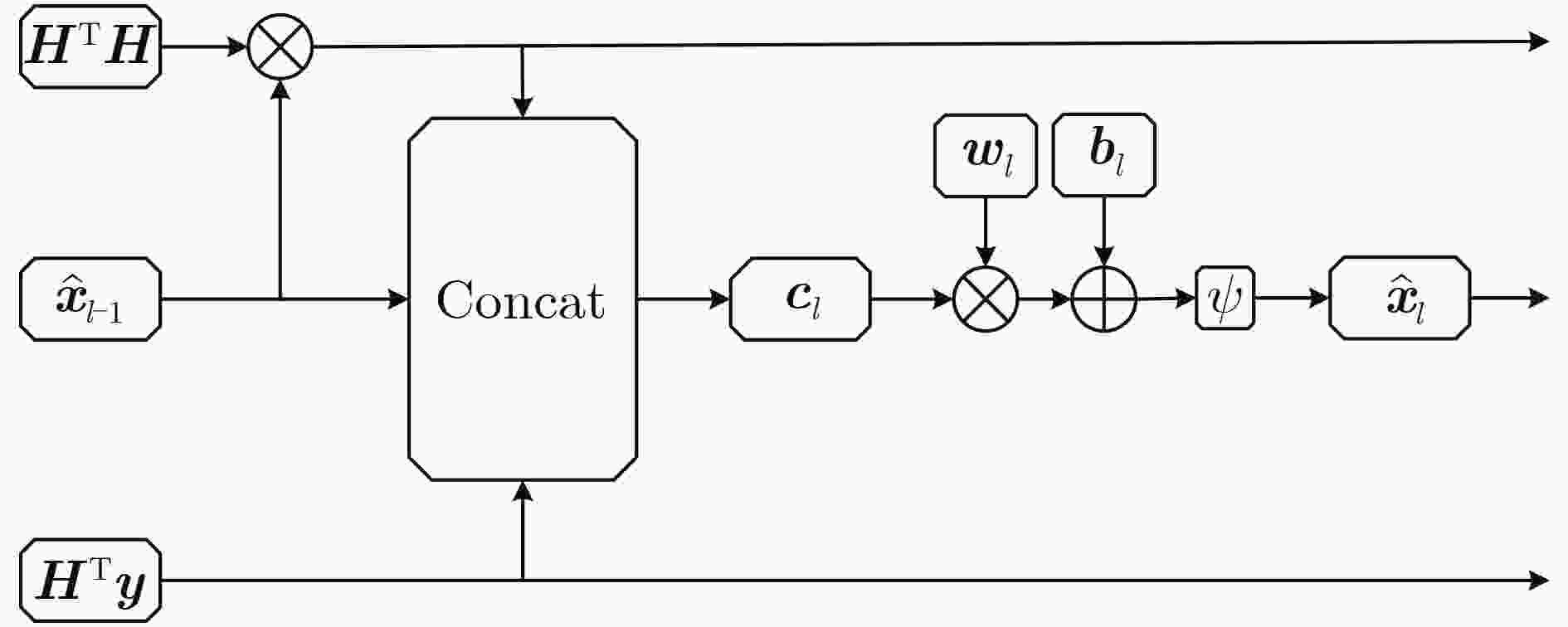
小,得到初步估计值${ {\boldsymbol{c} }_l} = {\left[ { { {\boldsymbol{H} }^{\text{T} } }{\boldsymbol{Hy} },{\text{diag} }({ {\boldsymbol{H} }^{\text{T} } }{\boldsymbol{H} }){ {\hat {\boldsymbol{x} } }_{l - 1} },{ {\hat {\boldsymbol{x} } }_{l - 1} } } \right]^{\text{T} } } $ ${\psi _t}(x) = - 1 + \dfrac{ {\rho (x + t)} }{ {|t|} } - \dfrac{ {\rho (x - t)} }{ {|t|} }$ $ { { {{\hat {\boldsymbol x}} } }_l} = {\psi _t}\left( { { {\boldsymbol{w} }_l}{ {\boldsymbol{c} }_l} + { {\boldsymbol{b} }_l} } \right) $ $ {\hat {\boldsymbol{x} } _l} = \alpha {\hat {\boldsymbol{x} } _{l - 1} } + (1 - \alpha ){\hat {\boldsymbol{x} } _l} $
$\mathcal{L}({\boldsymbol{x} },\hat {\boldsymbol{x} } ) = \displaystyle\sum\limits_{l = 1}^L {\ln } (l)\left[ { { {\left\| { {\boldsymbol{x} } - { { {\boldsymbol{\hat x} } }_l} } \right\|}^2} + \beta r({ {\hat {\boldsymbol{x} } }_l},{\boldsymbol{x} })} \right]$(3) 将得到的初步估计值解调到相应的星座点上
${\tilde x_j} = \mathop {\arg \min }\limits_{i \in \{ 1,2, \cdots ,{2^K}\} } |{\hat x_l}(j) - {s_i}|,j = 1,2, \cdots ,2M$(4) 再引入SIC,根据信道矩阵${\boldsymbol{H}}$列范数的大小来进行降序排序
$\mathcal{C} = \arg {{\rm{sort}}} \left( { {\gamma _1},{\gamma _2}, \cdots ,{\gamma _M} } \right)$$ {\gamma _m} = \left\| {{{\boldsymbol{h}}_m}} \right\|_2^2,\forall \:m = 1,2, \cdots ,M $ (5) 消除第$i (i = 1,2, \cdots ,2M)$个用户对下一个接收信号的影响,
并更新接收信号
${ { { {\tilde {\boldsymbol y} } } }_i} = \displaystyle\sum\limits_{k = 1}^i { { {\boldsymbol{h} }_k} } ({x_k} - { {\tilde x}_k}) + \displaystyle\sum\limits_{j = i + 1}^{2M} { { {\boldsymbol{h} }_j} } {x_j}$$ {{{{\tilde {\boldsymbol y}}}}_{i + 1}} = {{{\boldsymbol{\tilde y}}}_i} - {{\boldsymbol{h}}_{i + 1}}{{\tilde x}_{i + 1}}\left( {i = 1,2, \cdots ,2M} \right) $ (6) 得到更新的接收向量$ {{\tilde {\boldsymbol y}}} $、传输向量$ {{\tilde {\boldsymbol x}}} $和信道矩阵${\boldsymbol{H}}$再执行步
骤(2)(7) 重复步骤(3)—步骤(6),直到所有有用信号均被检测出来,
得到最终的检测信号向量${ { {\stackrel\smile{\boldsymbol{x} } } }_l}$表 2 训练ImpScNet-SIC时参数设置
参数名称 具体设置 发射天线数$M$ 4, 32, 64, 100, 128 接收天线数$N$ 4, 32, 64, 128 层数$L$ 15,15 起始学习率${\beta _0}$ 0.001 学习衰减率${\beta _t}$ 0.97 SNR(dB)范围 (4,14) 批量大小 500 训练网络迭代次数 10000 迭代周期 5 -
[1] RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: Opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40–60. doi: 10.1109/MSP.2011.2178495 [2] 李国权, 徐永海, 林金朝, 等. 基于深度学习的无线物理层关键技术研究综述[J]. 重庆邮电大学学报:自然科学版, 2020, 32(4): 503–510. doi: 10.3979/j.issn.1673-825X.2020.04.001LI Guoquan, XU Yonghai, LIN Jinchao, et al. A survey of wireless physical layer key technology based on deep learning[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2020, 32(4): 503–510. doi: 10.3979/j.issn.1673-825X.2020.04.001 [3] SUN Yi, ZHENG Le, ZHU Pengcheng, et al. On optimality of local maximum-likelihood detectors in large-scale MIMO channels[J]. IEEE Transactions on Wireless Communications, 2016, 15(10): 7074–7088. doi: 10.1109/TWC.2016.2596721 [4] MOHAMMADKARIMI M, MEHRABI M, ARDAKANI M, et al. Deep learning-based sphere decoding[J]. IEEE Transactions on Wireless Communications, 2019, 18(9): 4368–4378. doi: 10.1109/TWC.2019.2924220 [5] 申滨, 赵书锋, 金纯. 基于迭代并行干扰消除的低复杂度大规模MIMO信号检测算法[J]. 电子与信息学报, 2018, 40(12): 2970–2978. doi: 10.11999/JEIT180111SHEN Bin, ZHAO Shufeng, and JIN Chun. Low complexity iterative parallel interference cancellation detection algorithms for massive MIMO systems[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2970–2978. doi: 10.11999/JEIT180111 [6] 丁子哲, 张贤达. 基于串行干扰消除的V-BLAST检测[J]. 电子学报. 2007, 35(S1): 19–24.DING Zizhe and ZHANG Xianda. V-BLAST detection based on successive interference cancellation[J]. Acta Electronica Sinica, 2007, 35(S1): 19–24. [7] WANG Gang, WANG Dandan, and LI Daoben. An efficient ZF-SIC detection algorithm in MIMO CDMA system[C]. The 14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications, 2003. PIMRC 2003, Beijing, China, 2003: 1708–1711. [8] LIU T H. Some results for the fast MMSE-SIC detection in spatially multiplexed MIMO systems[J]. IEEE Transactions on Wireless Communications, 2009, 8(11): 5443–5448. doi: 10.1109/TWC.2009.090196 [9] SEEBÖCK P, WALDSTEIN S M, KLIMSCHA S, et al. Unsupervised identification of disease marker candidates in retinal OCT imaging data[J]. IEEE Transactions on Medical Imaging, 2019, 38(4): 1037–1047. doi: 10.1109/TMI.2018.2877080 [10] UMA M, SNEHA V, SNEHA G, et al. Formation of SQL from natural language query using NLP[C]. 2019 International Conference on Computational Intelligence in Data Science (ICCIDS), Chennai, India, 2019: 1–5. [11] BU Linkai and CHURCH T D. Perceptual speech processing and phonetic feature mapping for robust vowel recognition[J]. IEEE Transactions on Speech and Audio Processing, 2000, 8(2): 105–114. doi: 10.1109/89.824695 [12] XIA Junjuan, HE Ke, XU Wei, et al. A MIMO detector with deep learning in the presence of correlated interference[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4492–4497. doi: 10.1109/TVT.2020.2972806 [13] SUN Jianyong, ZHANG Yiqing, XUE Jiang, et al. Learning to search for MIMO detection[J]. IEEE Transactions on Wireless Communications, 2020, 19(11): 7571–7584. doi: 10.1109/TWC.2020.3012785 [14] HE Hengtao, WEN Chaokai, JIN Shi, et al. A model-driven deep learning network for MIMO detection[C]. 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, USA, 2018: 584–588. [15] LIAO Jieyu, ZHAO Junhui, GAO Feifei, et al. A model-driven deep learning method for massive MIMO detection[J]. IEEE Communications Letters, 2020, 24(8): 1724–1728. doi: 10.1109/LCOMM.2020.2989672 [16] TAN Xiaosi, XU Weihong, SUN Kai, et al. Improving massive MIMO message passing detectors with deep neural network[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1267–1280. doi: 10.1109/TVT.2019.2960763 [17] SAMUEL N, DISKIN T, and WIESEL A. Learning to detect[J]. IEEE Transactions on Signal Processing, 2019, 67(10): 2554–2564. doi: 10.1109/TSP.2019.2899805 [18] FENG Yuan, MA Yunsi, LI Zhengdai, et al. Low-complexity factor graph-based iterative detection for RRC-SEFDM signals[C]. 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2018: 1–6. [19] GAO Guili, DONG Chao, and NIU Kai. Sparsely connected neural network for massive MIMO detection[C]. 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 2018: 397–402. [20] DONG Fangwei, XIAO Yue, XIAO Lixia, et al. MF-SIC detector for massive MIMO with QPSK modulation[C]. 2015 IEEE/CIC International Conference on Communications in China - Workshops (CIC/ICCC), Shenzhen, China, 2015: 137–141. [21] TAKABE S, IMANISHI M, WADAYAMA T, et al. Trainable projected gradient detector for massive overloaded MIMO channels: Data-driven tuning approach[J]. IEEE Access, 2019, 7: 93326–93338. doi: 10.1109/access.2019.2927997 [22] ZHENG Peicong, ZENG Yuan, LIU Zhenrong, et al. Deep learning based trainable approximate message passing for massive MIMO detection[C]. 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 2020: 1–6. [23] SAMUEL N, DISKIN T, and WIESEL A. deep MIMO detection [C]. The 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 2017: 1–5. [24] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. [25] HE Hengtao, WEN Chaokai, JIN Shi, et al. Model-driven deep learning for MIMO detection[J]. IEEE Transactions on Signal Processing, 2020, 68: 1702–1715. doi: 10.1109/tsp.2020.2976585 -






 下载:
下载:



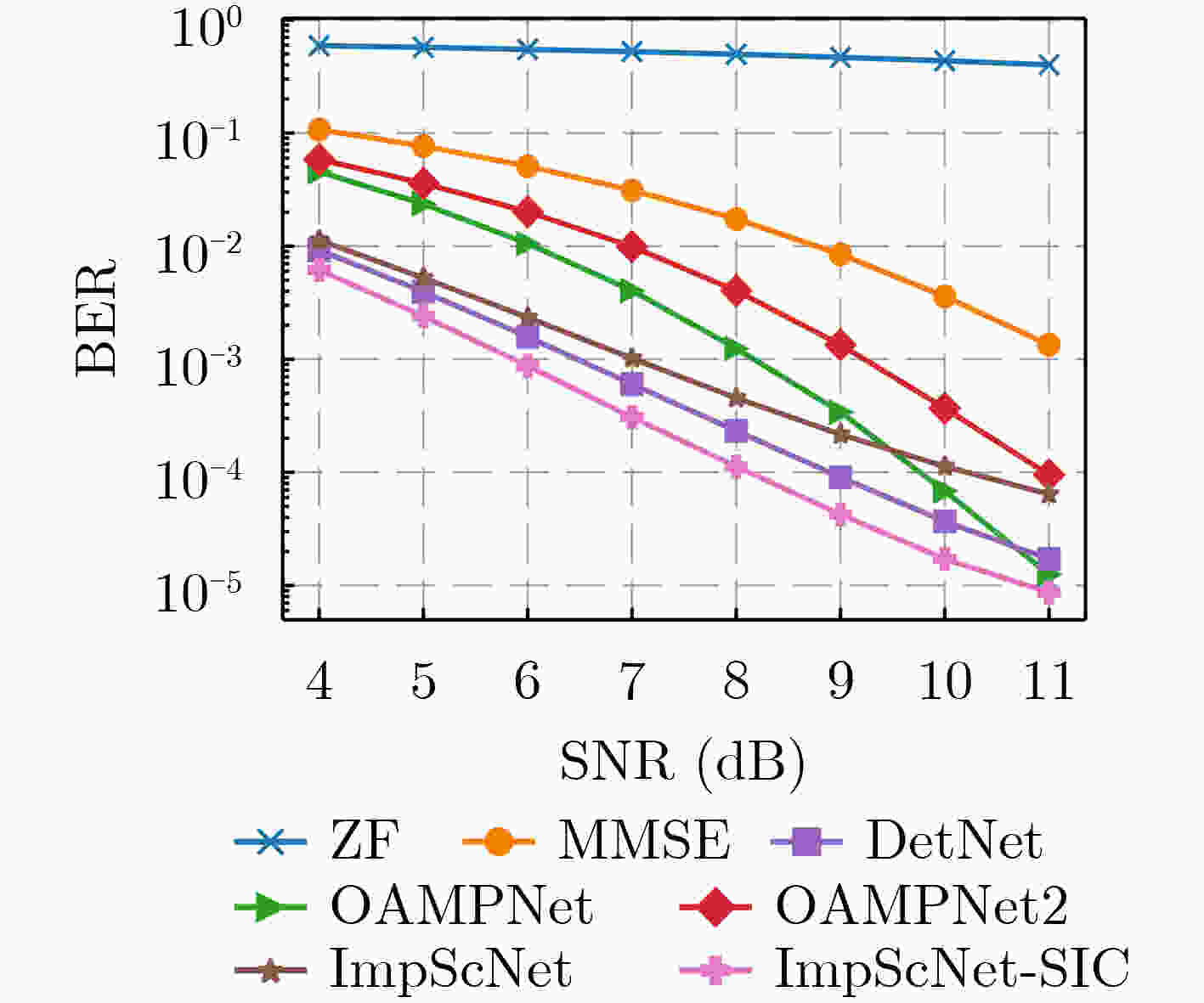

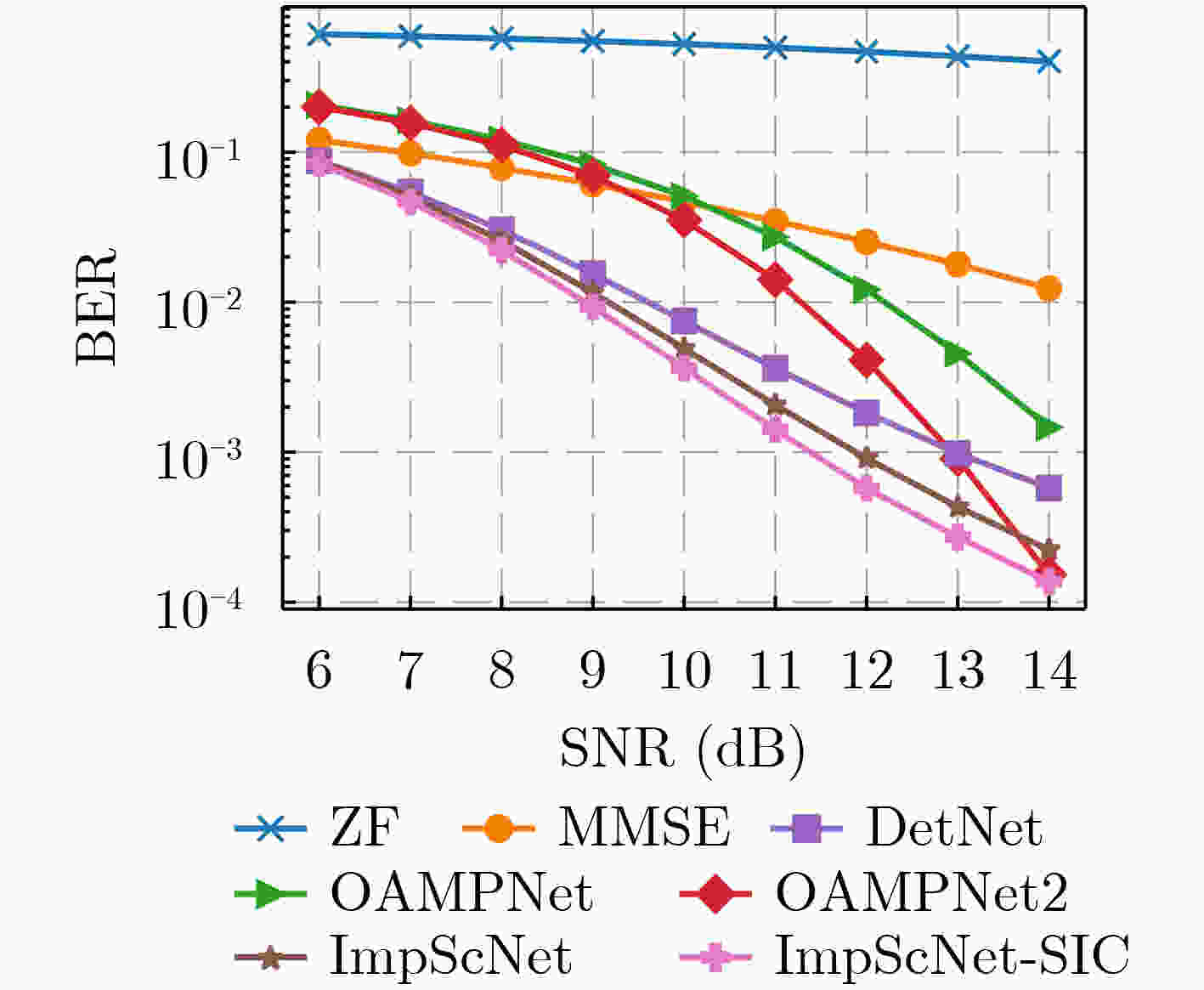



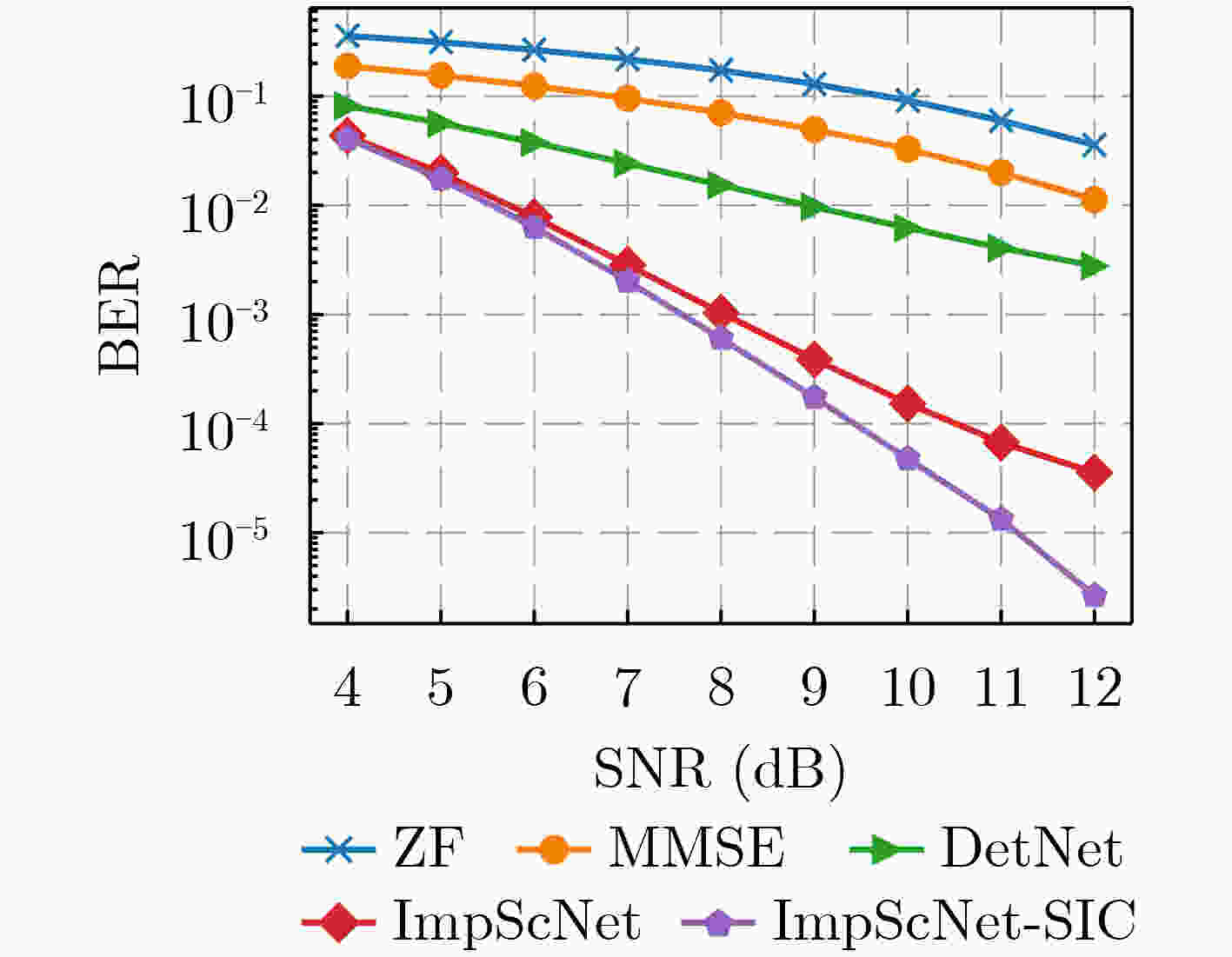

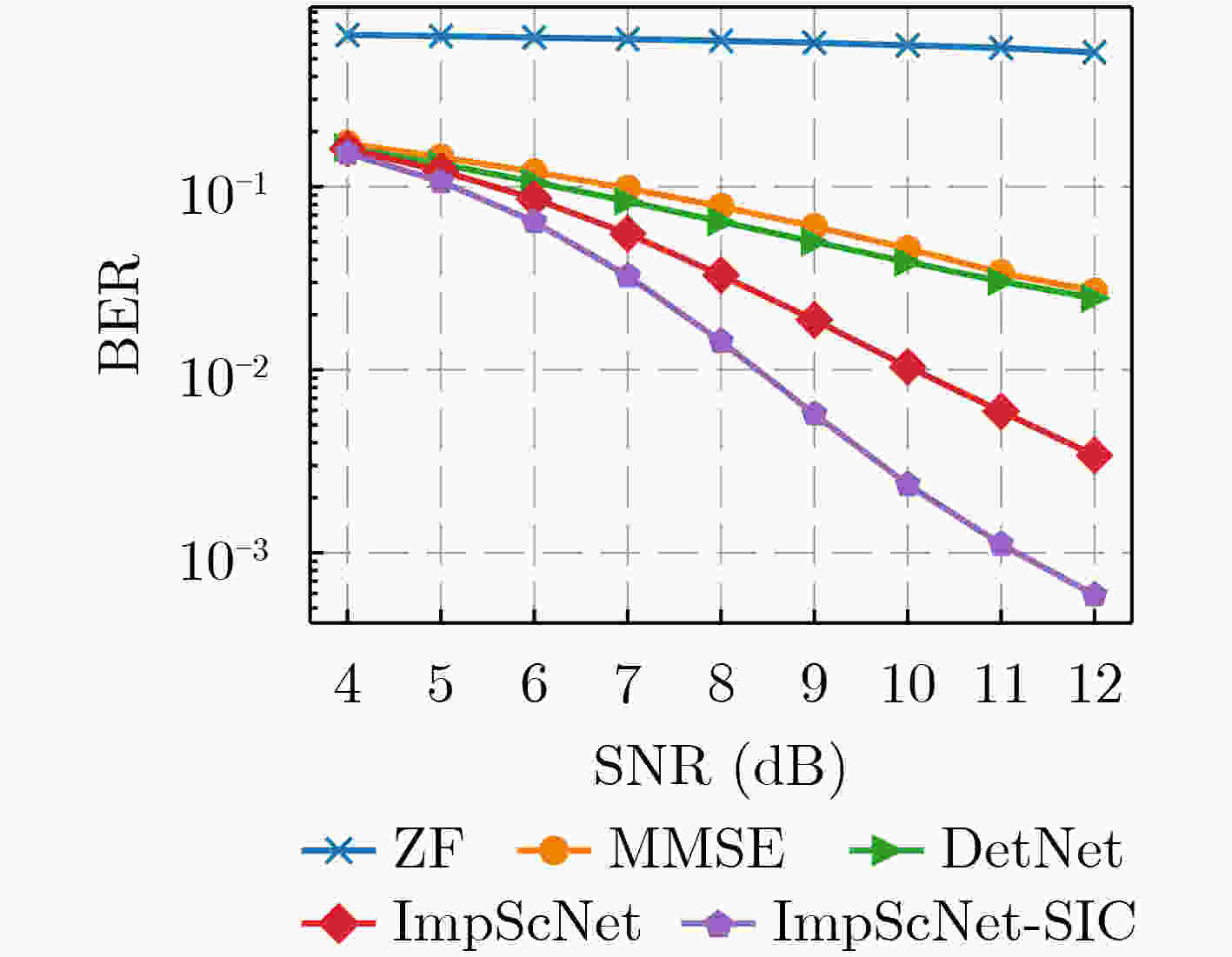



 下载:
下载:
