基于云模型的基本概率赋值生成方法及应用

国强; 文伟璐; 王亚妮; 戚连刚; Kaliuzhny Mykola

doi:10.11999/JEIT211259

基于云模型的基本概率赋值生成方法及应用

doi: 10.11999/JEIT211259

国强^{1, 2},
文伟璐^{1, 2},
王亚妮^{1, 2},
戚连刚^{1, 3, ,},
Kaliuzhny Mykola^{1, 4}

1.
哈尔滨工程大学信息与通信工程学院哈尔滨 150001
2.
先进船舶通信与信息技术工业和信息化部重点实验室哈尔滨 150001
3.
中国电子科技集团公司第十研究所敏捷智能计算四川省重点实验室成都 610036
4.
哈尔科夫国立无线电电子大学乌克兰哈尔科夫 61166

基金项目: 国家重点研发计划(2018YFE0206500)，国家自然科学基金(62071140)，国家国际科技合作专项(2015DFR10220)

详细信息

作者简介:
国强：男，教授，研究方向为电子对抗、智能信号处理与识别

文伟璐：女，硕士，研究方向为传感器信息融合、目标识别

王亚妮：女，博士生，研究方向为智能阵列信号处理、自适应干扰抑制

戚连刚：男，讲师，研究方向为自适应干扰抑制、卫星导航信号处理

Kaliuzhny Mykola：男，教授，研究方向为电子对抗、电磁目标识别

通讯作者:
戚连刚　qiliangang@hrbeu.edu.cn

中图分类号: TN911.7; TP391
计量
- 文章访问数: 522
- HTML全文浏览量: 271
- PDF下载量: 84
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-12
- 修回日期: 2022-10-07
- 录用日期: 2022-10-08
- 网络出版日期: 2022-10-13
- 刊出日期: 2023-03-10

Basic Probability Assignment Generation Method and Application Based on Cloud Model

GUO Qiang^{1, 2},
WEN Weilu^{1, 2},
WANG Yani^{1, 2},
QI Liangang^{1, 3
, ,},
Kaliuzhny Mykola^{1, 4}

1.
College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
2.
Key Laboratory of Advanced Marine Communication and Information Technology, Ministry of Industry and Information Technology, Harbin 150001, China
3.
Agile and Intelligent Computing Key Laboratory of Sichuan Province, Chengdu 610036, China
4.
Kharkiv National University of Radio Electronics, Kharkiv 61166, Ukraine

Funds: The National Key R & D Plan (2018YFE0206500), The National Natural Science Foundation of China (62071140), The National Special for International Scientific and Technological Cooperation (2015DFR10220)

摘要

摘要: 针对证据理论应用中基本概率赋值(BPA)生成模型难以确定问题，该文提出一种基于云模型的BPA生成方法。首先基于样本属性的正态云模型构建单子集命题的BPA模型函数，并将复合子集的模型函数表示为高斯函数乘积融合。其次提出一种根据测试样本动态度量属性权重的方法来兼顾信息源的可靠性。最后，用属性权重修正模型函数输出的结果得到BPA。鸢尾花等数据集分类识别实验表明，该方法识别准确性高，且适用于样本较少的情况。
- 目标识别 /
- 多源信息融合 /
- 证据理论 /
- 基本概率赋值 /
- 云模型
Abstract: Basic Probability Assignment (BPA) has no fixed generative model in the application of evidence theory. To solve this problem, a BPA generation method based on cloud model is proposed. Firstly, based on the normal cloud model of the sample attributes, the BPA model function of the single subset proposition is constructed, and the model function of the composite subset is expressed as Gaussian function product fusion. Secondly, a method of dynamically measuring attribute weights based on test samples is proposed to take into account the reliability of information sources. Finally, the BPA is obtained by modifying the output result of the model function with attribute weights. The classification and recognition experiments of iris and other data sets show that this method has high recognition accuracy and is suitable for situations with fewer samples.
- Target recognition /
- Multi-source information fusion /
- Evidence theory /
- Basic Probability Assignment (BPA) /
- Cloud model

HTML全文

图 1 两个高斯函数乘积

下载: 全尺寸图片幻灯片

图 2 正态云模型

下载: 全尺寸图片幻灯片

图 3 单子集模型函数与复合子集模型函数

下载: 全尺寸图片幻灯片

图 4 所提出方法的框图

下载: 全尺寸图片幻灯片

图 5 SL属性的隶属度曲线

下载: 全尺寸图片幻灯片

图 6 识别正确率与样本规模的关系

下载: 全尺寸图片幻灯片

表 1 SL属性下的模型参数

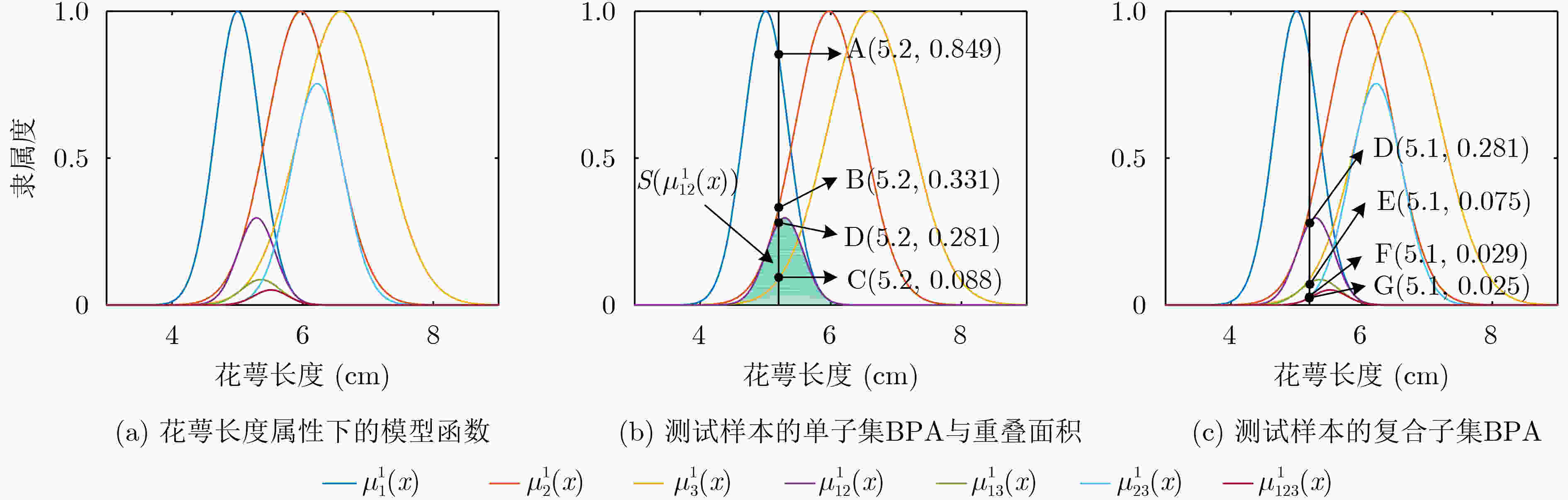
参数	$ \mu _1^1 $	$ \mu _2^1 $	$ \mu _3^1 $	$ \mu _{12}^1 $	$ \mu _{13}^1 $	$ \mu _{23}^1 $	$ \mu _{123}^1 $
$ {\text{Ex}} $	5.006	5.974	6.588	5.295	5.362	6.223	5.514
$ {\text{En}} $	0.339	0.520	0.630	0.284	0.299	0.401	0.259
$ {\text{Sg}} $				0.297	0.087	0.754	0.174

下载: 导出CSV

表 2 SL属性下计算的BPA

BPA	$ {\theta _1} $	$ {\theta _2} $	$ {\theta _3} $	$ {\theta _1}{\theta _2} $	$ {\theta _1}{\theta _3} $	$ {\theta _2}{\theta _3} $	$\varTheta$
$ {P_1}(\theta ) $	0.849	0.331	0.088	0.281	0.075	0.029	0.025
$P'_1 (\theta )$	0.506	0.197	0.053	0.167	0.045	0.017	0.015
$ {m_1}(\theta ) $	0.451	0.176	0.047	0.149	0.040	0.016	0.122

下载: 导出CSV

表 3 属性权重

属性	SL	SW	PL	PW
$ {p^j} $	1	2	2	2
$ {q^j} $	2	3	3	3
$ {w^j} $	0.891	0.710	0.919	0.954

下载: 导出CSV

表 4 BPA及其最大信度值对应焦元

BPA	$ {\theta _1} $	$ {\theta _2} $	$ {\theta _3} $	$ {\theta _1}{\theta _2} $	$ {\theta _1}{\theta _3} $	$ {\theta _2}{\theta _3} $	$\varTheta$	最大信度对应焦元
$ {m_1}(\theta ) $	0.451	0.176	0.047	0.149	0.040	0.016	0.122	$ {\theta _1} $
$ {m_2}(\theta ) $	0.028	0.196	0.132	0.027	0.019	0.130	0.469	$\varTheta$
$ {m_3}(\theta ) $	0	0.889	0.018	0	0	0.013	0.081	$ {\theta _2} $
$ {m_4}(\theta ) $	0	0.803	0.078	0	0	0.073	0.046	$ {\theta _2} $
$ m(\theta ) $	0.003	0.986	0.008	0	0	0.002	0	$ {\theta _2} $

下载: 导出CSV

表 5 识别结果(%)

方法	鸢尾花	葡萄酒	种子
文献[8]	94.00	84.82	88.10
文献[9]	93.33	91.18	88.10
文献[11]	94.67	86.50	87.14
文献[13]	92.00	92.09	86.67
文献[24]	94.67	88.69	90.48
本文方法	96.00	92.68	89.05

下载: 导出CSV

参考文献(24)

[1]	DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. The Annals of Mathematical Statistics, 1967, 38(2): 325–339. doi: 10.1214/aoms/1177698950
[2]	MI Xiangjun, LÜ Tongxuan, TIAN Ye, et al. Multi-sensor data fusion based on soft likelihood functions and OWA aggregation and its application in target recognition system[J]. ISA Transactions, 2021, 112: 137–149. doi: 10.1016/j.isatra.2020.12.009
[3]	LIU Peide, ZHANG Xiaohong, and PEDRYCZ W. A consensus model for hesitant fuzzy linguistic group decision-making in the framework of Dempster–Shafer evidence theory[J]. Knowledge-Based Systems, 2021, 212: 106559. doi: 10.1016/j.knosys.2020.106559
[4]	尹东亮, 黄晓颖, 吴艳杰, 等. 基于云模型和改进D-S证据理论的目标识别决策方法[J]. 航空学报, 2021, 42(12): 324768. doi: 10.7527/S1000-6893.2020.24768 YIN Dongliang, HUANG Xiaoying, WU Yanjie, et al. Target recognition decision method based on cloud model and improved D-S evidence theory[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(12): 324768. doi: 10.7527/S1000-6893.2020.24768
[5]	王万请, 赵拥军, 黄洁, 等. 基于信息守恒的基本概率赋值概率转换方法[J]. 电子与信息学报, 2013, 35(2): 457–462. WANG Wanqing, ZHAO Yongjun, HUANG Jie, et al. A transformation of basic probability assignment to probability based on conservation of information[J]. Journal of Electronics & Information Technology, 2013, 35(2): 457–462 .
[6]	ZHANG Jingfei and DENG Yong. A method to determine basic probability assignment in the open world and its application in data fusion and classification[J]. Applied Intelligence, 2017, 46(4): 934–951. doi: 10.1007/s10489-016-0877-9
[7]	JING Ming and TANG Yongchuan. A new base basic probability assignment approach for conflict data fusion in the evidence theory[J]. Applied Intelligence, 2021, 51(2): 1056–1068. doi: 10.1007/s10489-020-01876-0
[8]	康兵义, 李娅, 邓勇, 等. 基于区间数的基本概率指派生成方法及应用[J]. 电子学报, 2012, 40(6): 1092–1096. doi: 10.3969/j.issn.0372-2112.2012.06.004 KANG Bingyi, LI Ya, DENG Yong, et al. Determination of basic probability assignment based on interval numbers and its application[J]. Acta Electronica Sinica, 2012, 40(6): 1092–1096. doi: 10.3969/j.issn.0372-2112.2012.06.004
[9]	WANG Shuning and TANG Yongchuan. An improved approach for generation of a basic probability assignment in the evidence theory based on Gaussian distribution[J]. Arabian Journal for Science and Engineering, 2022, 47(2): 1595–1607. doi: 10.1007/s13369-021-06011-w
[10]	肖建于, 童敏明, 朱昌杰, 等. 基于广义三角模糊数的基本概率赋值构造方法[J]. 仪器仪表学报, 2012, 33(2): 429–434. doi: 10.3969/j.issn.0254-3087.2012.02.027 XIAO Jianyu, TONG Minming, ZHU Changjie, et al. Basic probability assignment construction method based on generalized triangular fuzzy number[J]. Chinese Journal of Scientific Instrument, 2012, 33(2): 429–434. doi: 10.3969/j.issn.0254-3087.2012.02.027
[11]	崔家玮. 证据理论中基本概率指派生成与合成方法研究[D]. [硕士论文], 解放军信息工程大学, 2014: 15–24. CUI Jiawei. Research on basic probability assignment derivation and combination in evidence theory[D]. [Master dissertation], Information Engineering University, 2014: 15–24.
[12]	蒋雯, 陈运东, 汤潮, 等. 基于样本差异度的基本概率指派生成方法[J]. 控制与决策, 2015, 30(1): 71–75. doi: 10.13195/j.kzyjc.2013.1706 JIANG Wen, CHEN Yundong, TANG Chao, et al. Determination of basic probability assignment based on sample difference degree[J]. Control and Decision, 2015, 30(1): 71–75. doi: 10.13195/j.kzyjc.2013.1706
[13]	JIANG Wen, ZHUANG Miaoyan, XIE Chunhe, et al. Sensing attribute weights: A novel basic belief assignment method[J]. Sensors, 2017, 17(4): 721. doi: 10.3390/s17040721
[14]	SHAFER G A. A Mathematical Theory of Evidence[M]. Princeton: Princeton University Press, 1976.
[15]	FARAGHER R. Understanding the basis of the Kalman filter via a simple and intuitive derivation [Lecture Notes][J]. IEEE Signal Processing Magazine, 2012, 29(5): 128–132. doi: 10.1109/MSP.2012.2203621
[16]	刘树德. 概率论与数理统计[M]. 北京: 人民邮电出版社, 2019: 126–131. LIU Shude. Probability Theory and Mathematical Statistics[M]. Beijing: Post & Telecom Press, 2019: 126–131.
[17]	阎少宏, 王宏. 模糊数学基础及应用[M]. 北京: 化学工业出版社, 2018: 13–17. YAN Shaohong and WANG Hong. Basis and Application of Fuzzy Mathematics[M]. Beijing: Chemical Industry Press, 2018: 13–17.
[18]	李海林, 郭崇慧, 邱望仁. 正态云模型相似度计算方法[J]. 电子学报, 2011, 39(11): 2561–2567. LI Hailin, GUO Chonghui, and QIU Wangren. Similarity measurement between normal cloud models[J]. Acta Electronica Sinica, 2011, 39(11): 2561–2567.
[19]	GAO Shuguo, ZHAO Jun, LIU Yunpeng, et al. Research into power transformer health assessment technology based on uncertainty of information and deep architecture design[J]. Mathematical Problems in Engineering, 2021, 2021: 8831872. doi: 10.1155/2021/8831872
[20]	王栋. 基于数据融合的机载多传感器目标识别[D]. [硕士论文], 上海交通大学, 2010. WANG Dong. The airborne multi-sensor target recognition based on data fusion[D]. [Master dissertation], Shanghai Jiao Tong University, 2010.
[21]	FISHER R A. UCI machine learning repository: Iris[EB/OL]. https://archive-beta.ics.uci.edu/ml/datasets/iris, 1988.
[22]	FORINA M. UCI machine learning repository: Wine[EB/OL]. https://archive-beta.ics.uci.edu/ml/datasets/wine, 1991.
[23]	CHARYTANOWICZ M, NIEWCZAS J, KULCZYCKI P, et al. UCI machine learning repository: Seeds[EB/OL]. https://archive-beta.ics.uci.edu/ml/datasets/seeds, 2012.
[24]	赵卫东, 董亮. 机器学习[M]. 北京: 人民邮电出版社, 2018: 64–78. ZHAO Weidong and DONG Liang. Machine Learning[M]. Beijing: Post & Telecom Press, 2018: 64–78.