Coalitional Graph Game Based Topology Control Algorithm for Unmanned Aerial Vehicle Emergency Networks in Underground Space
-
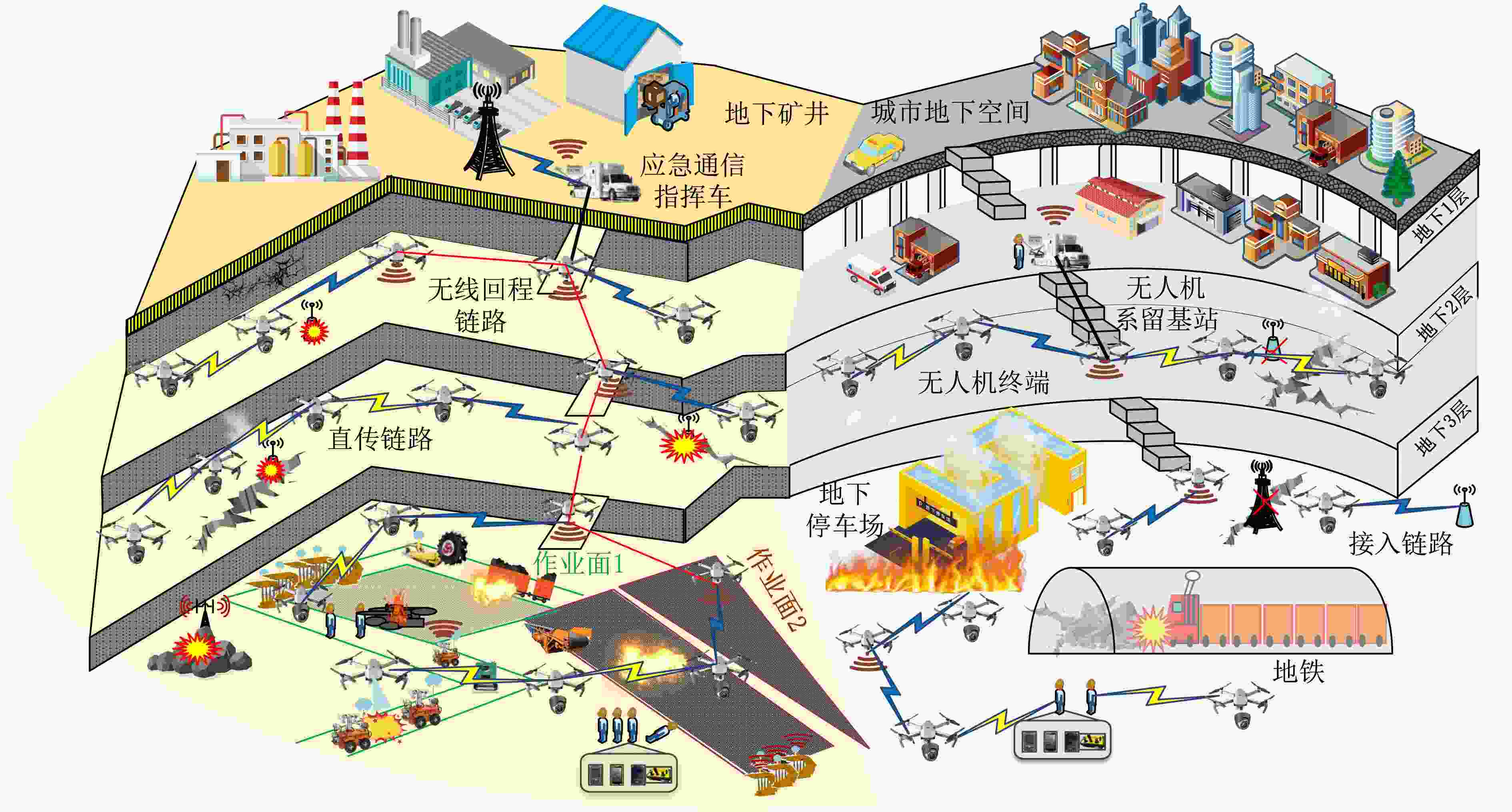
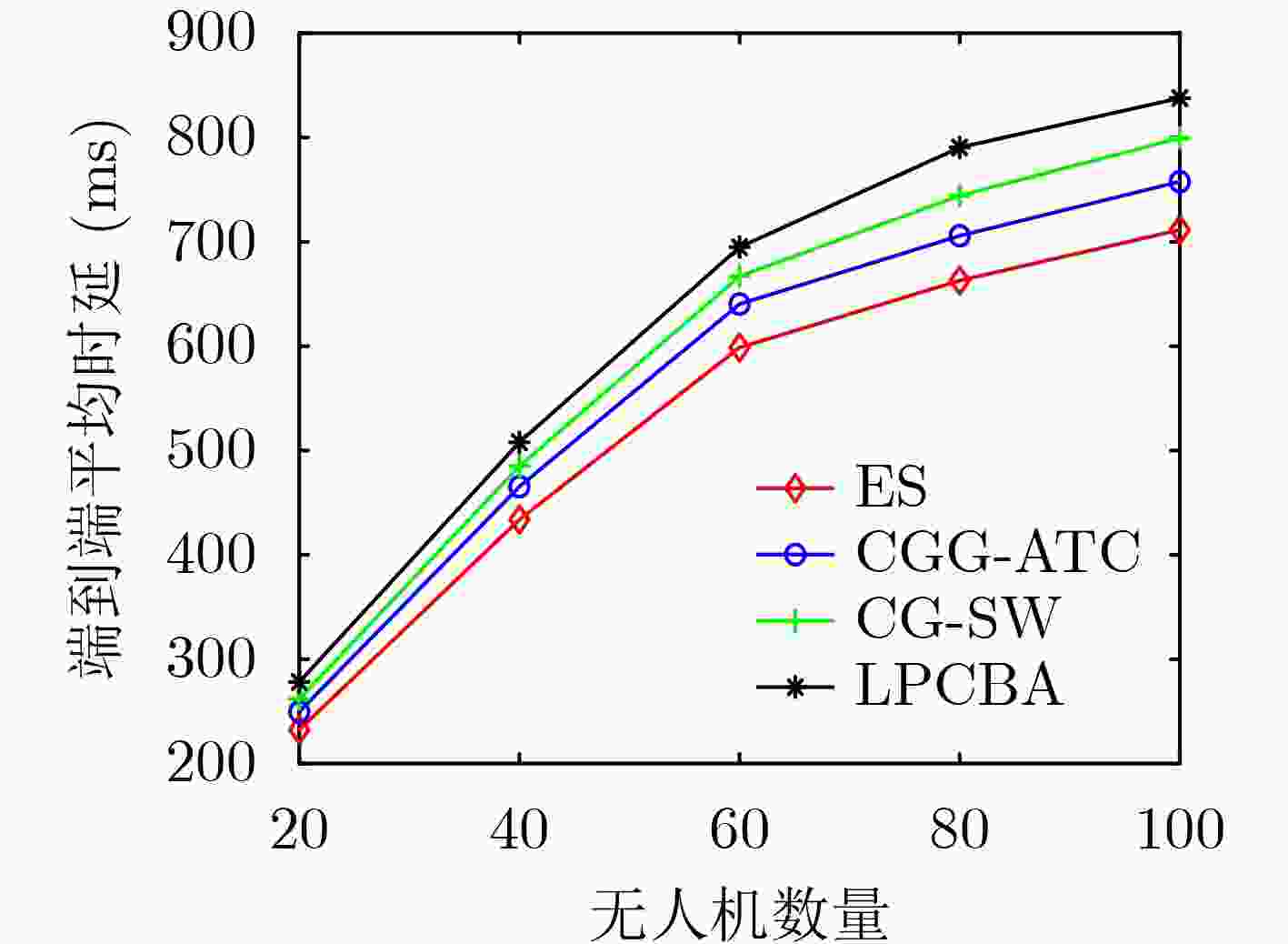
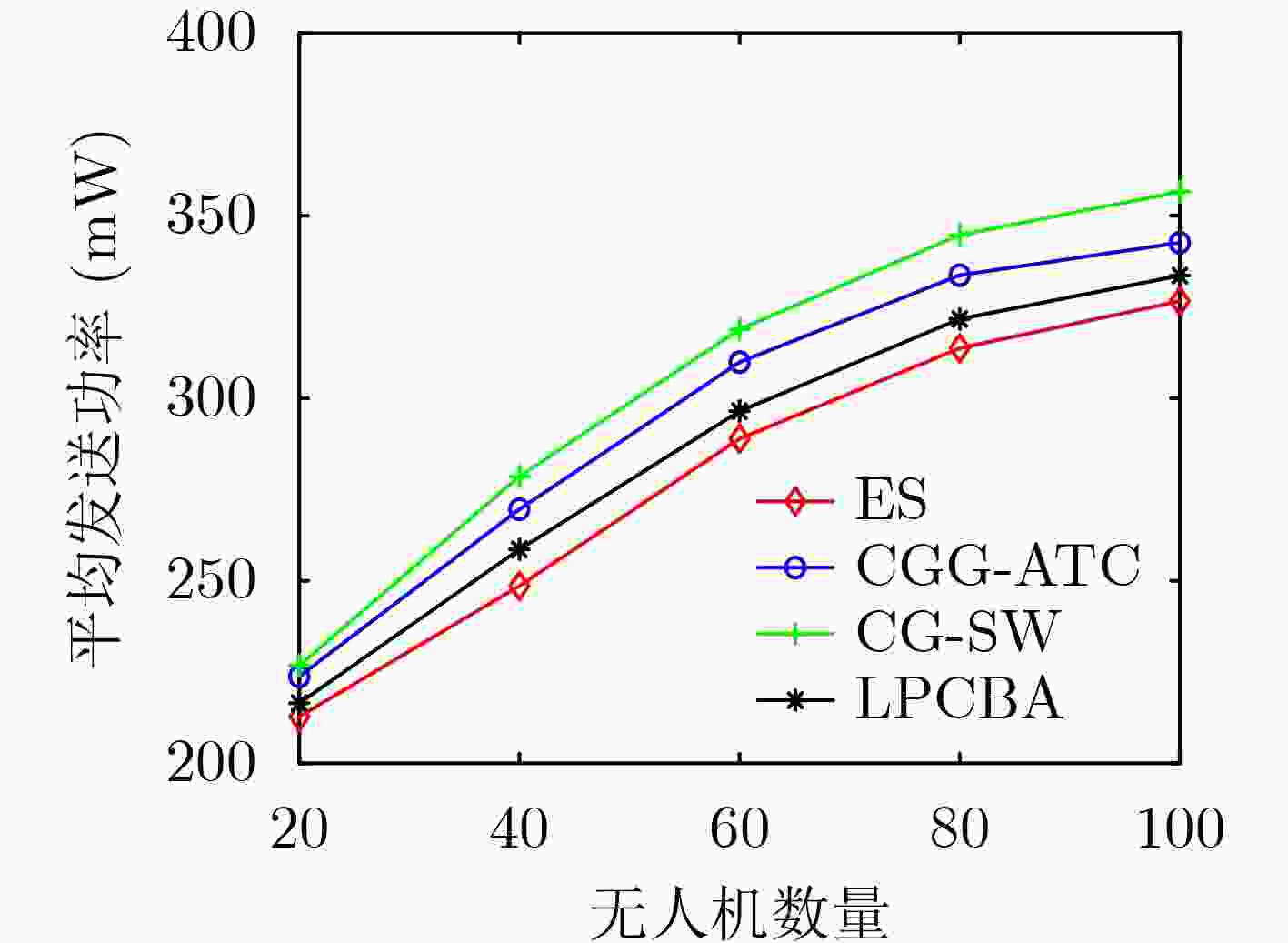
摘要: 地下空间灾害事故对极端环境下应急通信网络快速重组与灾情信息实时回传提出了严峻挑战,亟需构建具备按需动态重构、快速响应能力的无人机(UAV)应急通信网络。针对拓扑快变等动态不确定性造成的网络连通性频繁失效等问题,该文利用图论对时变拓扑的关键信息提取简化后,将联盟博弈(CG)引入时变拓扑图,提出一种基于联盟图博弈的自适应拓扑控制算法(CGG-ATC),通过协同决策建立远程传输链路(LLs)维护拓扑连通性。仿真结果表明,与其他现有算法相比,该算法能更好地实现拓扑连通性、平均传输时延与链路损耗3种性能之间的权衡优化。此外,该算法具有较快的收敛速度,能支持灾后动态不确定场景下组网决策随拓扑快变弹性适变。
-
关键词:
- 地下空间应急通信网络 /
- 无人机组网 /
- 拓扑控制 /
- 图论 /
- 博弈论
Abstract: Frequent disasters and accidents in underground space pose severe challenges to the rapid reconfiguration of emergency communication networks and the real-time transmission of disaster information in extreme environments. It is urgent to build the Unmanned Aerial Vehicle (UAV) emergency communication networks with the capabilities of dynamic reconstruction and real-time response. For the problems of frequent failure of network connectivity caused by dynamic uncertainties such as rapidly changing topologies, after extracting and simplifying the key topology information using graph theory, the Coalitional Game (CG) is combined with time-varying topology graphs and the Coalitional Graph Game based Adaptive Topology Control (CGG-ATC) algorithm, which can maintain the connectivity through collaborative establishment of Long-range Links (LLs), is proposed. The simulation results shows that the proposed algorithm can achieve the better trade-off among connectivity, average transmission delay, and link cost compared with other existing algorithms. Besides, due to its fast convergence speed, the network decision is elastic and adaptive with the rapid topology changes when considering the dynamic uncertainties of post-disaster scenarios. -
表 1 最大权轮转互操作联盟搜索(MWRS)算法
(1) 初始化:给定联盟结构${\varPi _t}$,UAV节点通过信息交换建立$ G_t^D $,每架UAV用一个1 bit标签表示当前状态:还未收到替换请求用白色表示,
已收到替换请求但未在环内用灰色表示,已在环用黑色表示,初始化所有节点标签为白色。${\text{ch}}({v_i})$为${v_i}$的子节点集,初始化$ {C_{{\text{mw}}}} $为空
集记录当前最大权有向环。(2) while $\exists {v_i} \in G_t^D$且${v_i}$标签为白 (3) 调用函数Traverse$\left( {{v_i}} \right)$遍历${v_i}$的子节点集,${v_i}$标签转换为灰色; (4) end while (5) Return $ {C_{{\text{mw}}}} $ (6) Traverse$\left( {{v_i}} \right)$: (7) for $\forall {v_j} \in {\text{ch}}\left( {{v_i}} \right)$ 执行 (8) If ${v_j}$为白色 (9) Traverse$\left( {{v_j}} \right)$; (10) else if ${v_j}$为灰色 (11) 找到环$C$; (12) If $C$权值之和大于${C_{{\rm{mw}}} }$的权值之和,环内没有节点在同一联盟内且环内任一边相连的 (13) 两个节点对之间交换次数不超过两次(避免乒乓球效应),$ {C_{{\text{mw}}}} = C $; (14) end if (15) else (16) 结束本次循环; (17) end if (18) end for 表 2 基于联盟图博弈的自适应拓扑控制(CGG-ATC)算法
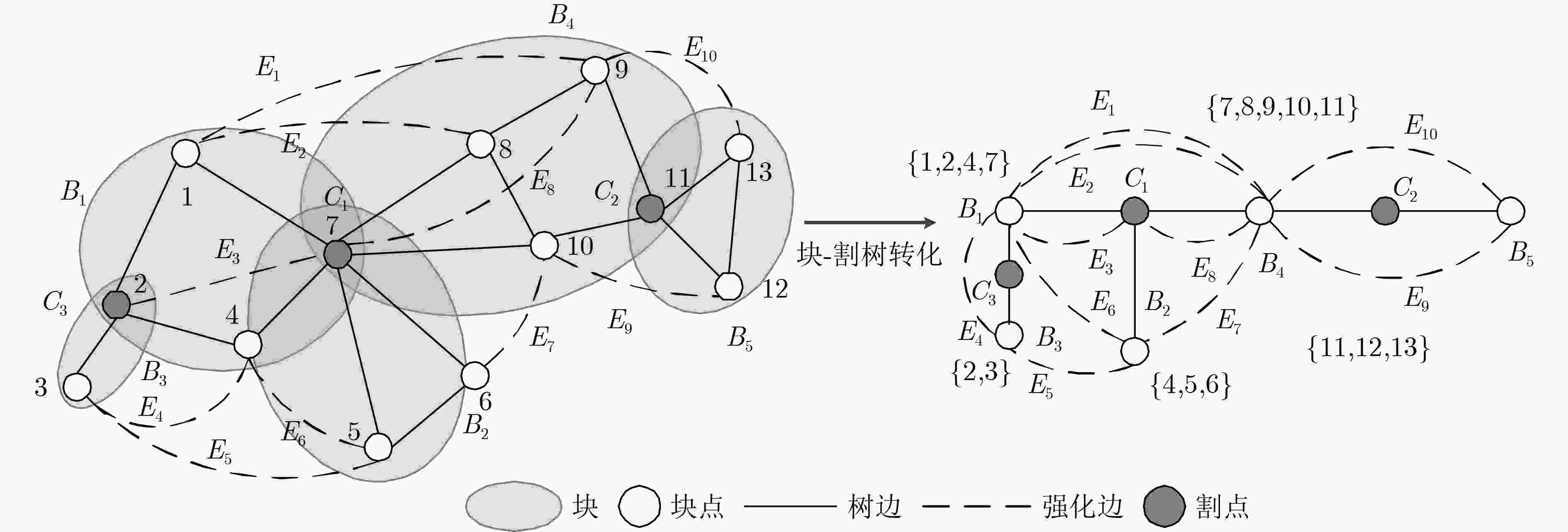
(1)步骤1 进入下一时刻$ t $ (2)根据拓扑结构变化更新时变拓扑图$ {G_t} = (V(t),E(t)) $,并转化为BCT确定最大联盟数$ K $并指导CGG重构与策略空间的简化,通过信息
交换更新效用函数值后,根据当前不稳定的联盟结构${\varPi _{t - 1} }$确定联盟转换意愿,初始时刻${\varPi _0}$通过随机联盟划分确定;(3)步骤2 轮转交换互操作 (4)根据联盟转换意愿建立$ G_t^D $,调用MWRS算法得到一个最大权轮转互操作联盟$ \left\{ {{v_1},{v_2},\cdots,{v_i}} \right\} $; (5) 执行轮转互换操作$ {v_1} \to {v_2} \to ,\cdots,{v_{i - 1}} \to {v_i} \to {v_1} $后得到当前联盟结构${\varPi _t}$; (6) 重复步骤2直到${\varPi _t}$中不存在轮转互操作联盟; (7) 输出NSE联盟策略${\varPi _t}$。 -
[1] 胡青松, 杨维, 丁恩杰, 等. 煤矿应急救援通信技术的现状与趋势[J]. 通信学报, 2019, 40(5): 163–179. doi: 10.11959/j.issn.1000-436x.2019123HU Qingsong, YANG Wei, DING Enjie, et al. State-of-the-art and trend of emergency rescue communication technologies for coal mine[J]. Journal on Communications, 2019, 40(5): 163–179. doi: 10.11959/j.issn.1000-436x.2019123 [2] YOU Xiaohu, WANG Chengxiang, HUANG Jie, et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts[J]. Science China Information Sciences, 2021, 64(1): 110301. doi: 10.1007/s11432-020-2955-6 [3] 徐常志, 靳一, 李立, 等. 面向6G的星地融合无线传输技术[J]. 电子与信息学报, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363XU Changzhi, JIN Yi, LI Li, et al. Wireless transmission technology of satellite-terrestrial integration for 6G mobile communication[J]. Journal of Electronics &Information Technology, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363 [4] DEEPAK G C, LADAS A, SAMBO Y A, et al. An Overview of post-disaster emergency communication systems in the future networks[J]. IEEE Wireless Communications, 2019, 26(6): 132–139. doi: 10.1109/MWC.2019.1800467 [5] 中华人民共和国应急管理部. 应急管理部信息化发展战略规划框架(2018-2022年)[EB/OL]. http://yjglt.jiangxi.gov.cn/art/2020/6/19/art_37823_1917424.html, 2020. [6] PARK S and CHOI Y. Applications of unmanned aerial vehicles in mining from exploration to reclamation: A review[J]. Minerals, 2020, 10(8): 663. doi: 10.3390/min10080663 [7] ZHAO Nan, LU Weidang, SHENG Min, et al. UAV-assisted emergency networks in disasters[J]. IEEE Wireless Communications, 2019, 26(1): 45–51. doi: 10.1109/MWC.2018.1800160 [8] BEKMEZCI İ, SAHINGOZ O K, and TEMEL Ş. Flying ad-hoc networks (FANETs): A survey[J]. Ad Hoc Networks, 2013, 11(3): 1254–1270. doi: 10.1016/j.adhoc.2012.12.004 [9] LAKEW D S, SA’AD U, DAO N N, et al. Routing in flying ad hoc networks: A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2020, 22(2): 1071–1120. doi: 10.1109/COMST.2020.2982452 [10] AZIZ A A, SEKERCIOGLU Y A, FITZPATRICK P, et al. A survey on distributed topology control techniques for extending the lifetime of battery powered wireless sensor networks[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 121–144. doi: 10.1109/SURV.2012.031612.00124 [11] QI Xiaohan, YUAN Peng, ZHANG Qinyu, et al. CDS-based topology control in FANETs via power and position optimization[J]. IEEE Wireless Communications Letters, 2020, 9(12): 2015–2019. doi: 10.1109/LWC.2020.3009666 [12] LJUBIĆ I and RAIDL G R. A memetic algorithm for minimum-cost vertex-biconnectivity augmentation of graphs[J]. Journal of Heuristics, 2003, 9(5): 401–427. doi: 10.1023/B:HEUR.0000004810.27436.30 [13] QI Xiaohan, JIN Haojie, ZHANG Qinyu, et al. A distributed bi-connectivity maintenance mechanism for flying ad hoc network Topology[C]. IEEE/CIC International Conference on Communications in China, Changchun, China, 2019: 961–966. [14] SAAD W, HAN Zhu, DEBBAH M, et al. Coalitional game theory for communication networks[J]. IEEE Signal Processing Magazine, 2009, 26(5): 77–97. doi: 10.1109/MSP.2009.000000 [15] MYERSON R B. Graphs and cooperation in games[J]. Mathematics of Operations Research, 1977, 2(3): 225–229. doi: 10.1287/moor.2.3.225 [16] ZHAO Yulei, LI Yong, MAO Hongliang, et al. Social-community-aware long-range link establishment for multihop D2D communication networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(11): 9372–9385. doi: 10.1109/TVT.2016.2516248 [17] WANG Bowen, SUN Yanjing, DO-DUY T, et al. Adaptive D-hop connected dominating set in highly dynamic flying ad-hoc networks[J]. IEEE Transactions on Network Science and Engineering, 2021, 8(3): 2651–2664. doi: 10.1109/TNSE.2021.3103873 [18] 吴坤, 谭劭昌. 基于改进鲸鱼优化算法的无人机航路规划[J]. 航空学报, 2020, 41(S2): 724286. doi: 10.7527/s1000-6893.2020.24286WU Kun and TAN Shaochang. Path planning of UAVs based on improved whale optimization algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724286. doi: 10.7527/s1000-6893.2020.24286 -





 下载:
下载:



 下载:
下载:
