面向接入回传一体化的毫米波空地网络建模与分析

卫海超; 邓娜; 朱近康

doi:10.11999/JEIT211177

面向接入回传一体化的毫米波空地网络建模与分析

doi: 10.11999/JEIT211177

1.
大连海事大学信息科学技术学院大连 116026
2.
大连理工大学信息与通信工程学院大连 116024
3.
中国科学技术大学信息科学技术学院合肥 230026

基金项目: 国家自然科学基金(61701071)，辽宁省自然科学基金(2021-MS-112)，中央高校基本科研业务费专项资金(DUT21JC04, 3132019348)

详细信息

作者简介:
卫海超：男，1989年生，讲师，研究方向为通信网络理论与技术、网络建模与分析、随机几何、无线定位技术

邓娜：女，1988年生，副教授，研究方向为通信网络理论与技术、网络建模与分析、基于无线大数据的网络设计、随机几何

朱近康：男，1943年生，教授，研究方向为绿色无线移动通信、新一代高效无线移动通信、无线移动通信信号处理等

通讯作者:
邓娜　dengna@dlut.edu.cn

¹⁾需要指出的是Nakagami衰落模型可以更好地模拟 LOS 链路传播特性，但导致更复杂的理论分析。同时，文献[15]表明Nakagami和瑞利衰落在用户性能体验上呈现相同的趋势。因此，本文采用更易分析的瑞利衰落模型。
中图分类号: TN929.5; V279
计量
- 文章访问数: 687
- HTML全文浏览量: 698
- PDF下载量: 96
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-28
- 修回日期: 2021-12-28
- 录用日期: 2021-12-31
- 网络出版日期: 2022-01-23
- 刊出日期: 2022-03-28

Modeling and Analysis of Millimeter-wave Air-terrestrial Networks with Integrated Access and Backhaul

1.
School of Information Science and Technology, Dalian Maritime University, Dalian 116026, China
2.
School of Information and Communication Engineering, Dalian University of Technology, Dalian 116024, China
3.
School of Information Science and Technology, University of Science and Technology of China, Hefei 230026, China

Funds: The National Natural Science Foundation of China (61701071), The Natural Science Foundation of Liaoning Province (2021-MS-112), The Fundamental Research Funds for the Central Universities (DUT21JC04, 3132019348)

摘要

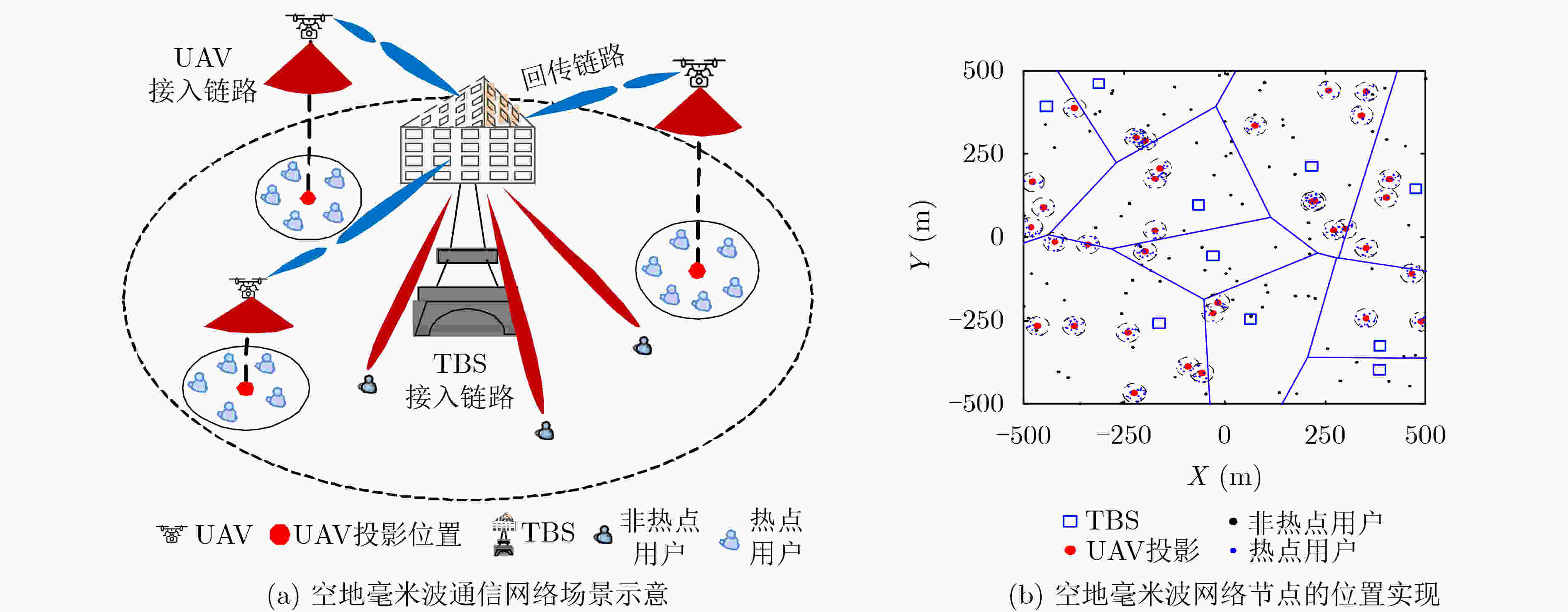
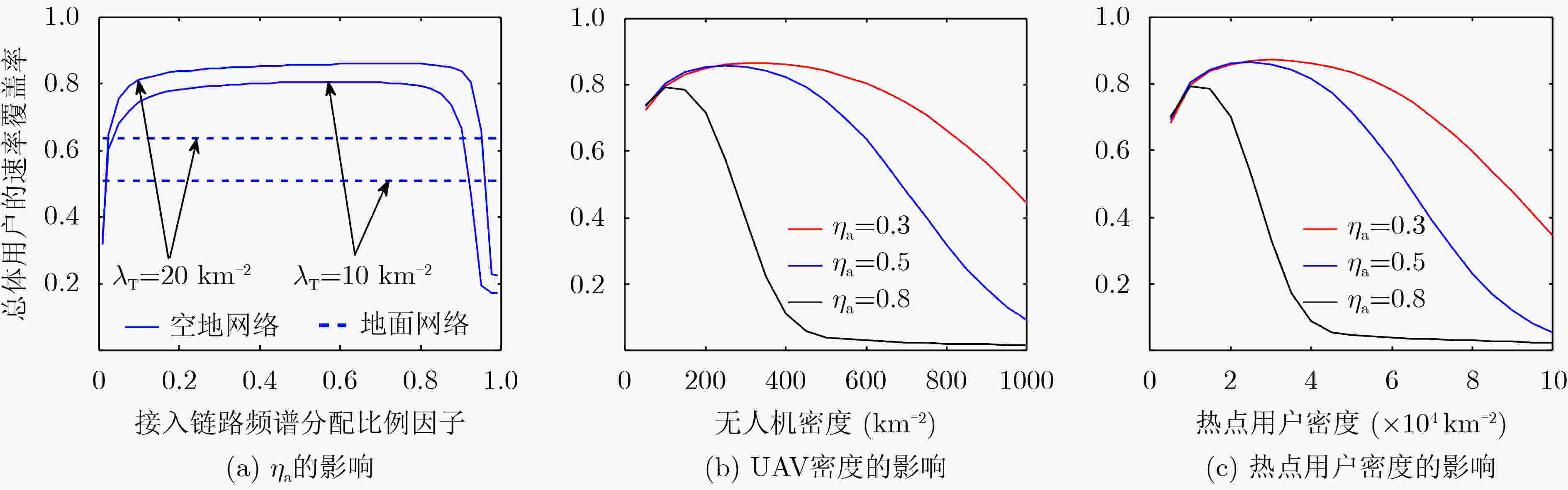
摘要: 无人机(UAV)作为空中基站有望成为传统地面网络的有力补充，以提供灵活覆盖和容量增强的解决方案。然而，大多现有研究忽略空中基站的无线回传这一实际因素对网络性能和用户体验的影响。为此，考虑接入回传一体化的空地毫米波蜂窝网络场景，其中无人机提供热点流量传输服务，地面基站(TBS)提供无人机回传链路并且服务非热点区域用户，以及接入和回传采用正交资源分配方法。针对该场景，提取地面基站、无人机和用户的空间分布特性，以及不同链路信号的传播特性，该文采用随机几何理论建立与之匹配的毫米波空地网络模型，推导了非热点用户的接入链路覆盖率和热点用户的接入回传链路的联合覆盖率。进一步地，基于地面基站和无人机的负载特性分析，推导了两种用户的速率覆盖率以及总体用户性能。基于所提分析框架，该文研究了关键系统参数，如接入链路频谱分配比例、无人机密度和热点用户密度等对用户性能的影响。
- 毫米波空地网络 /
- 接入回传一体化 /
- 性能分析 /
- 随机几何
Abstract: A millimeter-wave air-terrestrial network with integrated access and backhaul is considered to investigate the impact of the Unmanned Aerial Vehicle (UAV) wireless backhaul on the network performance and user experience, where UAVs provide hotspot traffic services, Terrestrial Base Stations (TBSs) provide UAV backhaul links and serve users in non-hotspot areas, and a spectrum partitioning resource allocation method is considered for the access and backhaul links. For this scenario, a stochastic geometry-based framework is established to model the millimeter wave air-ground network, and derive the coverage probabilities of both users. Furthermore, based on the load analysis of TBSs and UAVs, the rate coverage performances are provided as well as the overall user performance. Based on the proposed analytical framework, the impacts of key system parameters, such as access link spectrum allocation ratio, UAV, and hotspot user densities, on user performance are studied.
- Millimeter-wave air-terrestrial network /
- Integrated access and backhaul /
- Performance analysis /
- Stochastic geometry
¹⁾需要指出的是Nakagami衰落模型可以更好地模拟 LOS 链路传播特性，但导致更复杂的理论分析。同时，文献[15]表明Nakagami和瑞利衰落在用户性能体验上呈现相同的趋势。因此，本文采用更易分析的瑞利衰落模型。

HTML全文

图 1 空地毫米波通信网络场景

下载: 全尺寸图片幻灯片

图 2 基于用户SINR和速率覆盖率的理论结果与仿真验证

下载: 全尺寸图片幻灯片

图 3 总体用户的速率覆盖性能与关键系统参数的关系

下载: 全尺寸图片幻灯片

表 1 系统参数

参数	默认值
${\lambda _{\text{T}}},\;{\lambda _{\text{U}}},\;{\lambda _{{\text{TU}}}},\;{\lambda _{{\text{HU}}}}$	10 km^–2, 100 km^–2, 300 km^–2, 10000 km^–2
${\alpha _{\text{L}}},\;{\alpha _{\text{N}}},\;\varepsilon $	2.5, 4, –61 dB
$\beta ,\;A,\;B$	1/200, 11.95, 0.136
${\mu _{\text{T}}},\;{\mu _{\text{U}}}$	40 W, 20 W
$W,{\eta _a}$	1 GHz, 0.5
${N_0}$	–174 dBm/Hz+10log₁₀W +10 dB(噪声系数)
$h$	50 m
${G_{ij}},\;{g_{ij}},\;\;i \in \{ T,U\} ,j \in \{ {{a}},{{b}}\} $	18 dB, –2 dB
$ {\varphi _{ij}},\;\;i \in \{ T,U\} ,j \in \{ {{a}},{{b}}\} $	$ {\varphi _{{\text{Ua}}}} = 15^\circ $, 其他是10º

下载: 导出CSV

参考文献(18)

[1]	FOTOUHI A, QIANG Haoran, DING Ming, et al. Survey on UAV cellular communications: Practical aspects, standardization advancements, regulation, and security challenges[J]. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3417–3442. doi: 10.1109/COMST.2019.2906228
[2]	MOZAFFARI M, SAAD W, BENNIS M, et al. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems[J]. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2334–2360. doi: 10.1109/COMST.2019.2902862
[3]	PANG Xiaowei, TANG Jie, ZHAO Nan, et al. Energy-efficient design for mmWave-enabled NOMA-UAV networks[J]. Science China Information Sciences, 2021, 64(4): 140303. doi: 10.1007/S11432-020-2985-8
[4]	沈学民, 承楠, 周海波, 等. 空天地一体化网络技术: 探索与展望[J]. 物联网学报, 2020, 4(3): 3–19. doi: 10.11959/j.issn.2096−3750.2020.00142 SHEN Xuemin, CHENG Nan, ZHOU Haibo, et al. Space-air-ground integrated networks: Review and prospect[J]. Chinese Journal on Internet of Things, 2020, 4(3): 3–19. doi: 10.11959/j.issn.2096−3750.2020.00142
[5]	陈新颖, 盛敏, 李博, 等. 面向6G的无人机通信综述[J]. 电子与信息学报, 2022, 44(3): 781–789. CHEN Xinying, SHENG Min, LI Bo, et al. . Survey on unmanned aerial vehicle communications for 6G[J]. Journal of Electronics & Information Technology, 2022, 44(3): 781–789.
[6]	MADAPATHA C, MAKKI B, FANG Chao, et al. On integrated access and backhaul networks: Current status and potentials[J]. IEEE Open Journal of the Communications Society, 2020, 1: 1374–1389. doi: 10.1109/OJCOMS.2020.3022529
[7]	WANG Xianling, ZHANG Haijun, TIAN Yue, et al. Modeling and analysis of aerial base station-assisted cellular networks in finite areas under LoS and NLoS propagation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6985–7000. doi: 10.1109/TWC.2018.2865344
[8]	SUN Yanshi, DING Zhiguo, and DAI Xuchu. A user-centric cooperative scheme for UAV-assisted wireless networks in malfunction areas[J]. IEEE Transactions on Communications, 2019, 67(12): 8786–8800. doi: 10.1109/TCOMM.2019.2944911
[9]	AZARI M M, GERACI G, GARCIA-RODRIGUEZ A, et al. UAV-to-UAV communications in cellular networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(9): 6130–6144. doi: 10.1109/TWC.2020.3000303
[10]	KIM D, LEE J, and QUEK T Q S. Multi-layer unmanned aerial vehicle networks: Modeling and performance analysis[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 325–339. doi: 10.1109/TWC.2019.2944378
[11]	KOUZAYHA N, ELSAWY H, DAHROUJ H, et al. Analysis of large scale aerial terrestrial networks with mmWave backhauling[J]. IEEE Transactions on Wireless Communications, 2021, 20(12): 8362–8380. doi: 10.1109/TWC.2021.3092293
[12]	朱近康, 邓娜, 赵明. 蜂窝小区边缘同频嵌入垂直覆盖的网络性能[J]. 通信学报, 2015, 36(1): 2015002. doi: 10.11959/j.issn.1000-436x.2015002 ZHU Jinkang, DENG Na, and ZHAO Ming. Performance of cellular network embedded in the cell edge with vertical coverage by co-frequency[J]. Journal on Communications, 2015, 36(1): 2015002. doi: 10.11959/j.issn.1000-436x.2015002
[13]	BAI Tianyang and HEATH R W. Coverage and rate analysis for millimeter-wave cellular networks[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 1100–1114. doi: 10.1109/TWC.2014.2364267
[14]	AL-HOURANI A, KANDEEPAN S, and LARDNER S. Optimal LAP altitude for maximum coverage[J]. IEEE Wireless Communications Letters, 2014, 3(6): 569–572. doi: 10.1109/LWC.2014.2342736
[15]	DENG Na and HAENGGI M. A fine-grained analysis of millimeter-wave device-to-device networks[J]. IEEE Transactions on Communications, 2017, 65(11): 4940–4954. doi: 10.1109/TCOMM.2017.2725827
[16]	SAHA C and DHILLON H S. Millimeter wave integrated access and backhaul in 5G: Performance analysis and design insights[J]. IEEE Journal on Selected Areas in Communications, 2019, 37(12): 2669–2684. doi: 10.1109/JSAC.2019.2947997
[17]	FERENC J S and NÉDA Z. On the size distribution of Poisson Voronoi cells[J]. Physica A:Statistical Mechanics and its Applications, 2007, 385(2): 518–526. doi: 10.1016/j.physa.2007.07.063
[18]	HAENGGI M. Stochastic Geometry for Wireless Networks[M]. Cambridge: Cambridge University Press, 2012: 38–169.