A Multi-Scroll System and Its Application for Image Encryption Based on Logistic Level Pulse
-
摘要: 现有多涡卷吸引子混沌系统中引入的非线性函数多为阶梯函数、饱和函数、多逻辑电平脉冲函数等,从而系统的电路实现复杂度会随涡卷数量的增加而增大,致使其硬件实现变得较为困难。针对此问题,该文设计了Logistic电平脉冲函数,采用非自治的脉冲控制方法基于Lorenz系统构造了一个新的多涡卷混沌系统,对其进行了动力学特性分析和基于FPGA芯片的硬件实现,最后给出了系统在图像加密中的应用。分析结果表明,该文所设计系统的电路实现复杂度与涡卷数量无关,于是FPGA电路可在不改变RTL代码的情况下仅通过改变控制参数即可产生不同的多涡卷吸引子;与Lorenz系统相比,此多涡卷系统具有更多的敏感性参数,应用于图像加密时密钥空间更大,更能有效抵抗穷举攻击。
-
关键词:
- 混沌系统 /
- 图像加密 /
- 多涡卷吸引子 /
- Logistic映射 /
- FPGA
Abstract: The nonlinear functions introduced into the existing multi-scroll attractor chaotic systems are mostly step function, saturation function, multi-logic level pulse function and so on. Therefore, the system hardware complexity increases with the increase of the number of scrolls, which makes its hardware implementation more difficult. To solve this problem, a Logistic level pulse function is designed and a new chaotic system with multi-scroll based on the Lorenz system is constructed by the nonautonomous pulse control method. The system’s dynamic characteristics are analyzed and the system is implemented based on FPGA chip. Finally, the application of the system in image encryption is given. The analysis results show that the hardware complexity of the system designed in this paper is independent of the number of scrolls, so the FPGA circuit can produce different multi-scroll attractors only by changing the control parameters without the change of the RTL codes; Compared with the Lorenz system, the designed multi-scroll system has more sensitive parameters so as to have larger key space and resist brute-force attack more effectively when applied to image encryption.-
Key words:
- Chaotic System /
- Image encryption /
- Multi-scroll attractor /
- Logistic map /
- FPGA
-
表 1 NIST SP800-22随机特性测试结果
1 2 3 4 5 6 7 8 测试项目 单bit测试 块内单bit测试 游程测试 块内最长
游程测试二进制矩阵
秩测试离散傅里
叶测试非重叠模块
匹配测试重叠模块
匹配测试P-value 0.2270 0.8625 0.8341 0.7408 0.0134 0.9768 0.0634 0.4551 9 10 11 12 13 14 15 测试项目 Maurer通用统计测试 线性复杂度测试 序列测试 近似熵测试 累加和测试 随机旅行测试 随机旅行变种测试 P-value 0.0472 0.9422 0.4575 0.5921 0.6842 0.0719 0.0260 -
[1] LIU Yu, QIN Zheng, LIAO Xiaofeng, et al. A chaotic image encryption scheme based on Hénon–Chebyshev modulation map and genetic operations[J]. International Journal of Bifurcation and Chaos, 2020, 30(6): 2050090. doi: 10.1142/S021812742050090X [2] BAO Bocheng, HU Fengwei, QUAN Yajuan, et al. Self-excited and hidden attractors found simultaneously in a modified Chua's circuit[J]. International Journal of Bifurcation and Chaos, 2015, 25(5): 1550075. doi: 10.1142/S0218127415500753 [3] LIU Song, WEI Yaping, LIU Jingyi, et al. Multi-scroll chaotic system model and its cryptographic application[J]. International Journal of Bifurcation and Chaos, 2020, 30(13): 2050186. doi: 10.1142/S0218127420501862 [4] YU Simin, TANG W K S, LU Jinhu, et al. Generation of n×m -wing Lorenz-like attractors from a modified Shimizu-Morioka model[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2008, 55(11): 1168–1172. doi: 10.1109/TCSII.2008.2002563 [5] 摆玉龙, 杨阳, 唐丽红. 一个新多涡卷混沌系统的设计及在图像加密中的应用[J]. 电子与信息学报, 2021, 43(2): 436–444. doi: 10.11999/JEIT191002BAI Yulong, YANG Yang, and TANG Lihong. Design of a multi-scroll chaotic system and its application to image encryption[J]. Journal of Electronics &Information Technology, 2021, 43(2): 436–444. doi: 10.11999/JEIT191002 [6] YU Simin, Lü Jinhu, CHEN Guanrong, et al. Design and implementation of grid multiwing butterfly chaotic attractors from a piecewise Lorenz system[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2010, 57(10): 803–807. doi: 10.1109/TCSII.2010.2067792 [7] ZHANG Guitao and WNAG Faqian. A novel multi-scroll chaotic generator: Analysis, simulation, and implementation[J]. Chinese Physics B, 2018, 27(1): 018201. doi: 10.1088/1674-1056/27/1/018201 [8] CHEN Zhong, WEN Guilin, ZHOU Huaan, et al. Generation of grid multi-scroll chaotic attractors via hyperbolic tangent function series[J]. Optik, 2017, 130: 594–600. doi: 10.1016/j.ijleo.2016.10.085 [9] HONG Qinghui, LI Ya, WANG Xiaoping, et al. A versatile pulse control method to generate arbitrary multidirection multibutterfly chaotic attractors[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(8): 1480–1492. doi: 10.1109/TCAD.2018.2855121 [10] WU Qiujie, HONG Qinghui, LIU Xiaoyang, et al. Constructing multi-butterfly attractors based on Sprott C system via non-autonomous approaches[J]. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2019, 29(4): 043112. doi: 10.1063/1.5087976 [11] XIE Qi and ZENG Yicheng. Generating different types of multi-double-scroll and multi-double-wing hidden attractors[J]. The European Physical Journal Special Topics, 2020, 229(6): 1361–1371. doi: 10.1140/epjst/e2020-900223-9 [12] PENG Xuenan, ZENG Yicheng, WANG Mengjiao, et al. Generating multi-layer nested chaotic attractor and its FPGA implementation[J]. Chinese Physics B, 2021, 30(6): 060509. doi: 10.1088/1674-1056/abda34 [13] 陈志刚, 梁涤青, 邓小鸿, 等. Logistic混沌映射性能分析与改进[J]. 电子与信息学报, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039CHEN Zhigang, LIANG Diqing, DENG Xiaohong, et al. Performance analysis and improvement of logistic chaotic mapping[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039 [14] 孙克辉, 贺少波, 朱从旭, 等. 基于C0算法的混沌系统复杂度特性分析[J]. 电子学报, 2013, 41(9): 1765–1771. doi: 10.3969/j.issn.0372-2112.2013.09.015SUN Kehui, HE Shaobo, ZHU Congxu, et al. Analysis of chaotic complexity characteristics based on C0 algorithm[J]. Acta Electronica Sinica, 2013, 41(9): 1765–1771. doi: 10.3969/j.issn.0372-2112.2013.09.015 [15] CHUMAN T, SIRICHOTEDUMRONG W, and KIYA H. Encryption-then-compression systems using grayscale-based image encryption for JPEG images[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(6): 1515–1525. doi: 10.1109/TIFS.2018.2881677 -





 下载:
下载:

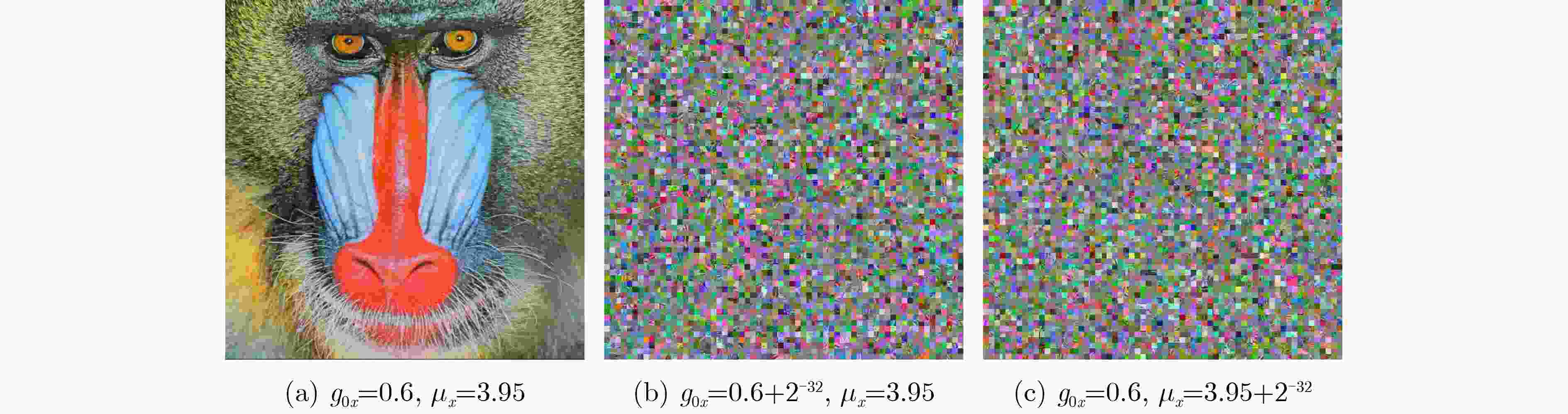


 下载:
下载:
