一种使用改进预测成本矩阵任务优先排序的异构计算系统列表调度算法

姚宇; 宋宇鲲; 杨国伟; 黄英; 张多利

doi:10.11999/JEIT211150

一种使用改进预测成本矩阵任务优先排序的异构计算系统列表调度算法

doi: 10.11999/JEIT211150

合肥工业大学微电子学院合肥 230601

基金项目: 安徽高校协同创新项目(GXXT-2019-030)

详细信息

作者简介:
姚宇：男，博士生，研究方向为多核片上网络系统编译技术

宋宇鲲：男，副研究员，研究方向为片上网络优化、多核系统设计、数字信号处理的VLSI实现

杨国伟：女，硕士生，研究方向为可重构计算技术

黄英：女，教授，博士生导师，研究方向为敏感材料与传感器技术

张多利：男，研究员，博士生导师，研究方向为多核处理器体系架构和设计方法

通讯作者:
张多利　zhangduoli@hfut.edu.cn

中图分类号: TN401
计量
- 文章访问数: 880
- HTML全文浏览量: 543
- PDF下载量: 133
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-21
- 修回日期: 2022-01-12
- 录用日期: 2022-01-20
- 网络出版日期: 2022-02-03
- 刊出日期: 2023-01-17

A List Scheduling Algorithm for Heterogeneous Computing Systems Using Improved Predict Cost Matrix for Task Prioritizing

School of Microelectronics, Hefei University of Technology, Hefei 230601, China

Funds: The University Synergy Innovation Program of Anhui Province (GXXT-2019-030)

摘要

摘要: 异构计算系统执行应用效率的提高高度依赖有效的调度算法。该文提出一种新的列表调度算法，称为改进的预测优先任务和乐观处理器选择调度(IPPOSS)。通过在任务优先级排序阶段引入任务的后向预测成本，来减少调度长度。与现有工作相比，该文使用改进预测成本矩阵(IPCM)，更合理地进行了任务优先级排序，从而在处理器选择阶段获得了更好的解，并保持2次时间复杂度。IPCM考虑了任务优先级排序阶段的各种计算、通信因素，比预测优先任务调度(PPTS)提出的预测成本矩阵(PCM)更容易获得合理的优先级列表。随机生成应用的有向无环图(DAG)和真实世界应用的DAG的实验结果分析表明，IPPOSS的性能优于相关算法。
- 异构系统 /
- 并行计算 /
- 列表调度 /
- 静态调度
Abstract: The improvement of application efficiency of heterogeneous computing systems is highly dependent on effective scheduling algorithms. A new list scheduling algorithm called Improved Predict Priority and Optimistic processor Selection Scheduling (IPPOSS) is proposed by this paper. By introducing the backward prediction cost of tasks in task prioritizing phase, the scheduling length is reduced. Compared with the existing work, an Improved Predict Cost Matrix (IPCM) is adopted to prioritize tasks more reasonably and a better solution in processor selection phase when keeping quadratic time complexity is obtain. IPCM, which considers various calculation and communication factors in the task prioritization stage, is easier to obtain a reasonable priority list than Predict Cost Matrix (PCM) proposed by Predict Priority Task Scheduling (PPTS). That the performance of IPPOSS is better than related algorithms is shown by the analysis of the experimental results of randomly generated application Directed Acyclic Graphs (DAGs) and real-world application DAGs.
- Heterogeneous systems /
- Parallel computing /
- List scheduling /
- Static scheduling

HTML全文

图 1 具有10 任务和3 处理器的任务以及计算消耗

下载: 全尺寸图片幻灯片

图 2 4种算法对图1中DAG1产生的调度结果

下载: 全尺寸图片幻灯片

图 3 4种算法对不同任务数量的DAG的调度结果

下载: 全尺寸图片幻灯片

图 4 4种算法对不同ccr的DAG的调度结果

下载: 全尺寸图片幻灯片

图 5 4种算法对不同处理器数量的DAG的调度结果

下载: 全尺寸图片幻灯片

图 6 4种算法对不同矩阵尺寸的高斯消元应用的调度结果

下载: 全尺寸图片幻灯片

图 7 4种算法对不同任务数量的蒙太奇应用的调度结果

下载: 全尺寸图片幻灯片

表 1 计算消耗

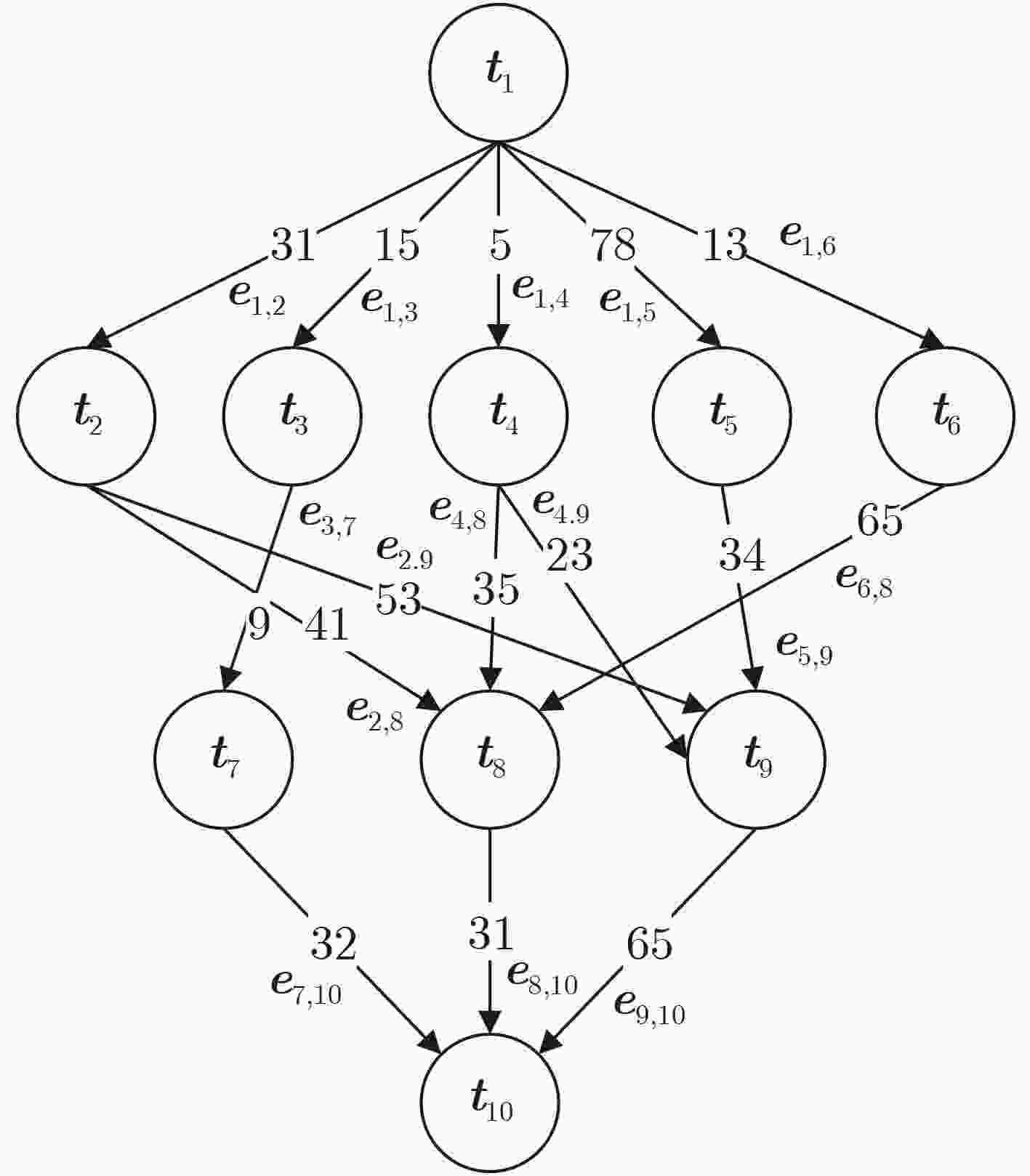
任务	p₁	p₂	p₃
t₁	6	45	4
t₂	13	12	34
t₃	45	23	34
t₄	5	33	4
t₅	3	16	42
t₆	23	54	7
t₇	99	56	34
t₈	54	13	44
t₉	75	13	87
t₁₀	84	32	37

下载: 导出CSV

表 2 图 1 中 DAG1 的 IPCM

任务	p₁	p₂	p₃
t₁	218	242	214
t₂	156	102	177
t₃	196	174	176
t₄	130	123	129
t₅	127	106	166
t₆	178	144	162
t₇	195	120	108
t₈	149	77	118
t₉	204	77	161
t₁₀	84	32	37

下载: 导出CSV

表 3 图 1 中 DAG1 的各算法任务优先级列表

任务	${\text{ran}}{{\text{k}}_\mu }$	${\text{ran}}{{\text{k}}_{{\text{OCT}}}}$	${\text{ran}}{{\text{k}}_{{\text{PCM}}}}$	${\text{ran}}{{\text{k}}_{{\text{IPCM}}}}$
t₁	325.0	114.0	224.0	224.7
t₂	247.0	80.3	137.3	145.0
t₃	189.0	77.0	182.0	182.0
t₄	211.3	68.3	145.7	127.3
t₅	228.7	67.7	128.7	133.0
t₆	212.0	78.7	162.7	161.3
t₇	146.0	44.3	122.7	141.0
t₈	119.0	44.0	97.7	114.7
t₉	174.3	51.0	120.3	147.3
t₁₀	51.0	0	51.0	51.0

下载: 导出CSV

表 4 不同方法的SLR对比(%)

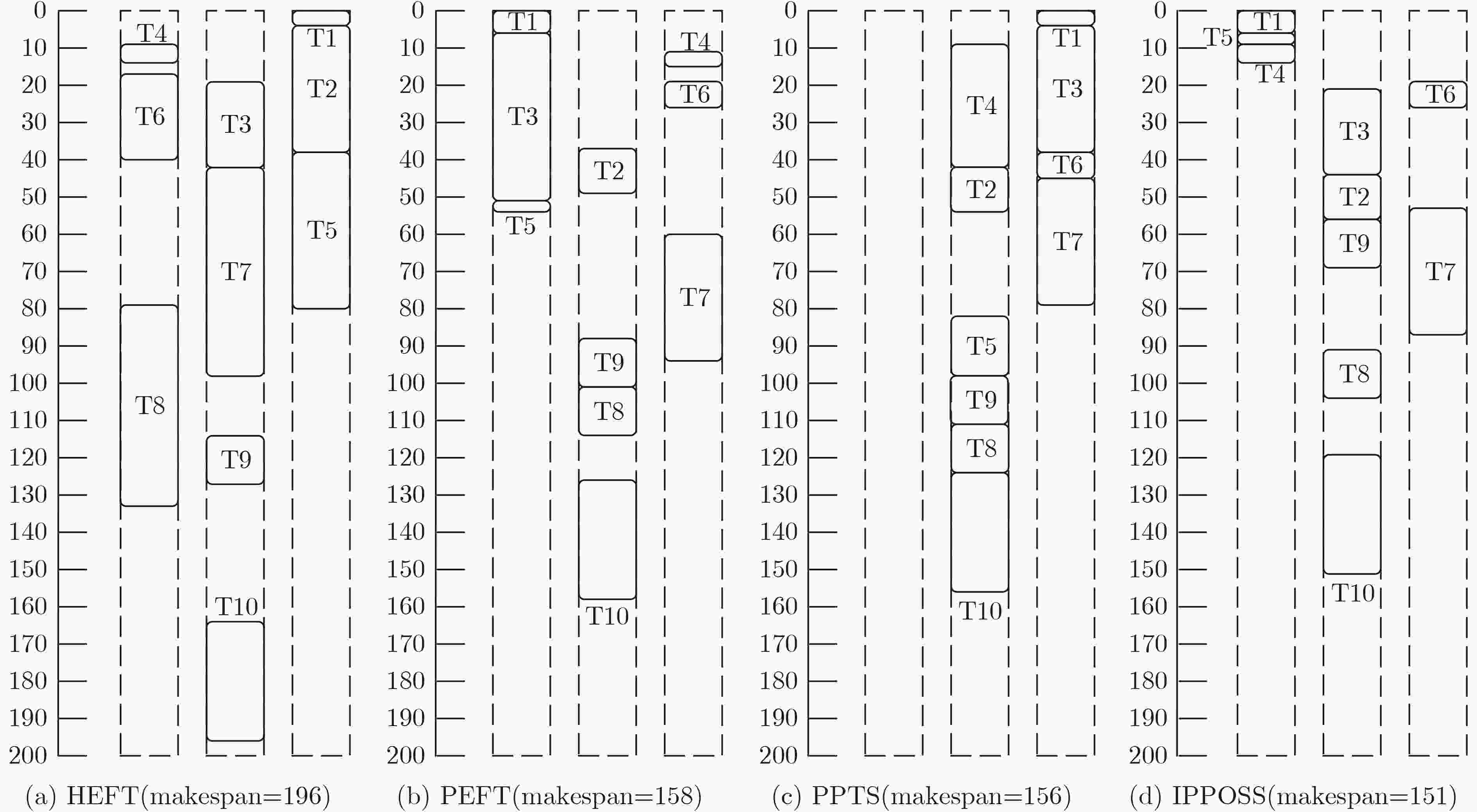
	PEFT	PPTS	IPPOSS with EFT_OCT
更好	57.50	35.90	16.30
相同	13.40	29.90	41.70
更差	29.10	34.10	42.00
平均降低	1.75	0.13	–0.48

下载: 导出CSV

算法1　IPPOSS算法
(1) 从出口任务到入口任务递归地为每个任务计算${\text{IPCM}}$和${\text{OCT}}$
(2) 计算所有任务的 ${\text{ran}}{{\text{k}}_{{\text{IPCM}}}}$
(3) 更新就绪列表
(4) while 就绪列表非空 do
(5) 　　${{\mathbf{t}}_i} \leftarrow $就绪列表中具有最高 ${\text{ran}}{{\text{k}}_{{\text{IPCM}}}}({{\mathbf{t}}_i})$的任务
(6) 　　for ${{\mathbf{p}}_m} \in {\mathbf{P}}$
(7) 　　　　使用基于插入的策略计算${\text{EFT(}}{{\mathbf{t}}_i},{{\mathbf{p}}_m}{\text{)}}$
(8) 　　　　计算$ {\text{EF}}{{\text{T}}_{{\text{OCT}}}}({{\mathbf{t}}_i},{{\mathbf{p}}_m}) $
(9) 　　end for
(10) 　　为${{\mathbf{t}}_i}$选择可以最小化$ {\text{EF}}{{\text{T}}_{{\text{OCT}}}}({{\mathbf{t}}_i},{{\mathbf{p}}_m}) $的${{\mathbf{p}}_m}$
(11) 　　更新就绪列表
(12) end while

下载: 导出CSV

表 5 4种算法的调度长度的成对比较(%)

		IPPOSS	PPTS	PEFT	HEFT
IPPOSS	更好相同更差	*	44.9 32.4 22.7	58.8 26.0 15.2	66.7 9.7 23.5
PPTS	更好相同更差	22.7 32.4 44.9	*	57.3 11.5 31.1	63.5 9.2 27.3
PEFT	更好相同更差	15.2 26.0 58.8	31.1 11.5 57.3	*	54.2 5.0 40.8
HEFT	更好相同更差	23.5 9.7 66.7	27.3 9.2 63.5	40.8 5.0 54.2	*

下载: 导出CSV

参考文献(26)

[1]	SINNEN O and SOUSA L A. Communication contention in task scheduling[J]. IEEE Transactions on Parallel and Distributed Systems, 2005, 16(6): 503–515. doi: 10.1109/TPDS.2005.64
[2]	GAREY M R, JOHNSON D S, and STOCKMEYER L. Some simplified NP-complete problems[C]. The 6th Annual ACM Symposium on Theory of Computing, Seattle, USA, 1974: 47–63.
[3]	ULLMAN J D. NP-complete scheduling problems[J]. Journal of Computer and System Sciences, 1975, 10(3): 384–393. doi: 10.1016/S0022-0000(75)80008-0
[4]	PAPADIMITRIOU C H and YANNAKAKIS M. Scheduling interval-ordered tasks[J]. SIAM Journal on Computing, 1979, 8(3): 405–409. doi: 10.1137/0208031
[5]	AGUILAR J and GELENBE E. Task assignment and transaction clustering heuristics for distributed systems[J]. Information Sciences, 1997, 97(1/2): 199–219. doi: 10.1016/S0020-0255(96)00178-8
[6]	HUANG Kuochan, GU D S, LIU H C, et al. Task clustering heuristics for efficient execution time reduction in workflow scheduling[J]. Journal of Computers, 2017, 28(1): 43–56. doi: 10.3966/199115592017022801004
[7]	TIAN Qiao, LI Jingmei, XUE Di, et al. A hybrid task scheduling algorithm based on task clustering[J]. Mobile Networks and Applications, 2020, 25(4): 1518–1527. doi: 10.1007/s11036-019-01356-x
[8]	SULAIMAN M, HALIM Z, WAQAS M, et al. A hybrid list-based task scheduling scheme for heterogeneous computing[J]. The Journal of Supercomputing, 2021, 77(9): 10252–10288. doi: 10.1007/s11227-021-03685-9
[9]	AHMAD W and ALAM B. An efficient list scheduling algorithm with task duplication for scientific big data workflow in heterogeneous computing environments[J]. Concurrency and Computation:Practice and Experience, 2021, 33(5): e5987. doi: 10.1002/cpe.5987
[10]	HAGRAS T, ATEF A, and MAHDY Y B. Greening duplication-based dependent-tasks scheduling on heterogeneous large-scale computing platforms[J]. Journal of Grid Computing, 2021, 19(1): 13. doi: 10.1007/s10723-021-09554-2
[11]	TOPCUOGLU H, HARIRI S, and WU Minyou. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13(3): 260–274. doi: 10.1109/71.993206
[12]	BITTENCOURT L F, SAKELLARIOU R, and MADEIRA E R M. DAG scheduling using a lookahead variant of the heterogeneous earliest finish time algorithm[C]. The 2010 18th Euromicro Conference on Parallel, Distributed and Network-Based Processing, Pisa, Italy, 2010: 27–34.
[13]	ARABNEJAD H and BARBOSA J G. List scheduling algorithm for heterogeneous systems by an optimistic cost table[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 25(3): 682–694. doi: 10.1109/TPDS.2013.57
[14]	DJIGAL H, FENG Jun, and LU Jiamin. Task scheduling for heterogeneous computing using a predict cost matrix[C]. The 48th International Conference on Parallel Processing: Workshops, Kyoto, Japan, 2019: 25.
[15]	ZHAO Yi, CAO Suzhi, and YAN Lei. List scheduling algorithm based on pre-scheduling for heterogeneous computing[C]. 2019 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking, Xiamen, China, 2019: 588–595.
[16]	IJAZ S and MUNIR E U. MOPT: List-based heuristic for scheduling workflows in cloud environment[J]. The Journal of Supercomputing, 2019, 75(7): 3740–3768. doi: 10.1007/s11227-018-2726-6
[17]	DOROSTKAR F and MIRZAKUCHAKI S. List scheduling for heterogeneous computing systems introducing a performance-effective definition for critical path[C]. The 2019 9th International Conference on Computer and Knowledge Engineering, Mashhad, Iran, 2019: 356–362.
[18]	JIANG Chao, WANG Jinlin, and YE Xiaozhou. PVBTS: A novel task scheduling algorithm for heterogeneous computing platforms[J]. International Journal of Innovative Computing, Information and Control, 2020, 16(2): 701–713. doi: 10.24507/ijicic.16.02.701
[19]	GHOLAMI H and ZAKERIAN R. A list-based heuristic algorithm for static task scheduling in heterogeneous distributed computing systems[C]. The 2020 6th International Conference on Web Research, Tehran, Iran, 2020: 21–26.
[20]	HU Wei, GAN Yu, LV Xiangyu, et al. A improved list heuristic scheduling algorithm for heterogeneous computing systems[C]. 2020 IEEE International Conference on Systems, Man, and Cybernetics, Toronto, Canada, 2020: 1111–1116.
[21]	HU Wei, GAN Yu, WEN Yuan, et al. An improved heterogeneous dynamic list schedule algorithm[C]. The 20th International Conference on Algorithms and Architectures for Parallel Processing, New York City, USA, 2020: 159–173.
[22]	DJIGAL H, FENG Jun, LU Jiamin, et al. IPPTS: An efficient algorithm for scientific workflow scheduling in heterogeneous computing systems[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(5): 1057–1071. doi: 10.1109/TPDS.2020.3041829
[23]	SHI Zhiao, JEANNOT E, and DONGARRA J J. Robust task scheduling in non-deterministic heterogeneous computing systems[C]. 2006 IEEE International Conference on Cluster Computing, Barcelona, Spain, 2006: 1–10.
[24]	frs69wq. DAGGEN: A synthetic task graph generator[EB/OL].https://github.com/frs69wq/daggen, 2021.
[25]	AMOURA A K, BAMPIS E, and KONIG J C. Scheduling algorithms for parallel Gaussian elimination with communication costs[J]. IEEE Transactions on Parallel and Distributed Systems, 1998, 9(7): 679–686. doi: 10.1109/71.707547
[26]	JIANG Qingye, LEE Y C, ARENAZ M, et al. Optimizing scientific workflows in the cloud: A montage example[C]. The 2014 IEEE/ACM 7th International Conference on Utility and Cloud Computing, London, UK, 2014: 517–522.