A Geometric Reconstrction Method for Predicting Shape of Irregular Rocks under Moon’s Subsurface Using Lunar Penetrating Radar Based on a Deep Learning Algorithm
-
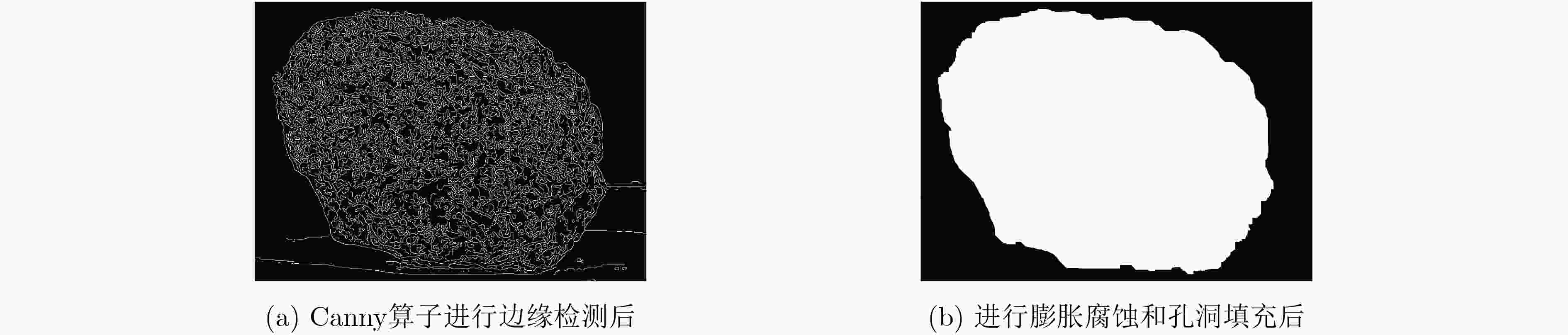
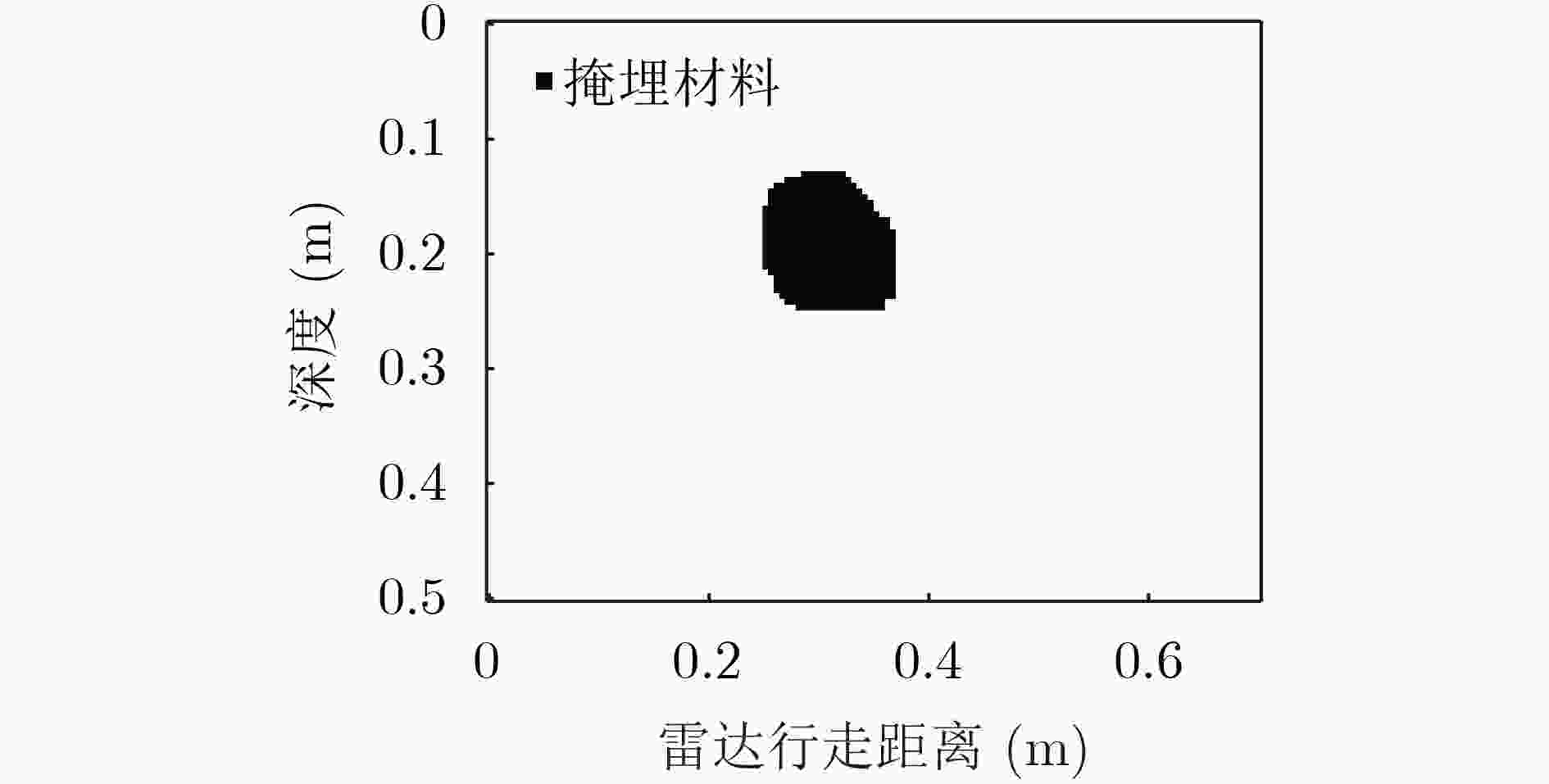
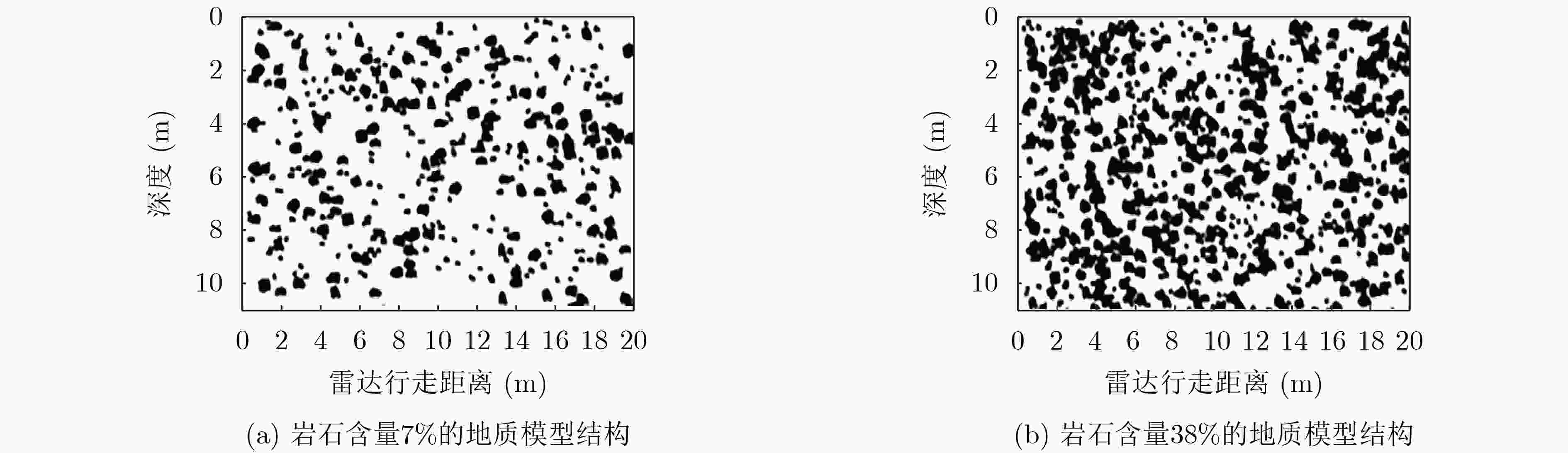
摘要: 在月壤中掩埋的岩块几何形状和电性特征分布具有显著的不确定性,探月雷达(LPR)获得的回波信号的特征复杂,无法有效地对月壤内部结构进行精确的几何成像。该文提出一种基于主成分分析降维的深度学习数据处理方法,用于复杂月表以下岩石分布结构的快速数字化成像,可以直接建立回波信号特征与月岩几何拓扑的关联关系。首先基于Apollo探月任务返回的月岩样品照片,利用边缘检测等图像处理方法提取月岩介质的几何轮廓,构建含有月岩块体的地层模型;针对信息冗余的时域回波信号,采用主成分分析法对高维空间的回波数据进行降维处理,然后利用基于均方根传递(RMSprop)的反向传播算法构建针对月岩介质上表面轮廓和位置的拟合预测模型。仿真结果表明,对于掩埋的具有复杂几何特征和高介电常数的单月岩块地层结构,深度学习R-square确定系数可达到0.93,月岩上表面轮廓和位置预测结果与真实模型重合度较高;同时也对复杂多月岩随机分布模型进行了探索性神经网络几何重建建模和验证。此工作为后续地质科学领域开展基于数据驱动模型的地层成像相关研究提供了初步的参考。Abstract: The subsurface structure and composition of moon are always heterogeneous, also, both geometric shape of buried materials and electromagnetic characteristics of formations are complicated. Therefore, it is very challenging to interpret Lunar Penetrating Radar (LPR) data and segment subsurface layers accurately and reliably. In this paper, deep learning method is utilized to reconstruct geological models from simulated LPR signal dataset. First, the geometric contours of lunar rock are extracted based on the photos of the lunar rock samples from Apollo 14, using image edge detection. The principal component analysis method is used to reduce the dimensionality of LPR data. Then, using the back propagation algorithm based on Root Mean Square prop (RMSprop), an artificial neural network is built to predict geometric characteristics of single buried basaltic rock. The results show that the depth of the buried rock with high-contrast dielectric constant and complex geometric features has been predicted with high accuracies, with the R-square of 0.93. Also, an artificial neural network model is also created to reconstruct geometric characteristics of heterogeneous model with randomly distributed lunar rocks. The preliminary results provide an initial attempt for development of data-driven subsurface imaging techniques in the geoscience field.
-
表 1 探月雷达的参数设计
名称 0.5 m深探月雷达
主要参数和技术指标10 m深探月雷达
主要参数和技术指标中心频率(MHz) 1200 700 动态范围(dB) ≥48 ≥96 探测深度(m) ≥0.5 ≥10 深度分辨率(cm) ≤2 ≤20 表 2 月壤电性参数表
密度(g/cm3) 介电常数 损耗正切角 样本编号 1.081 1.704 0.0085 75061 表 3 月岩电性参数表
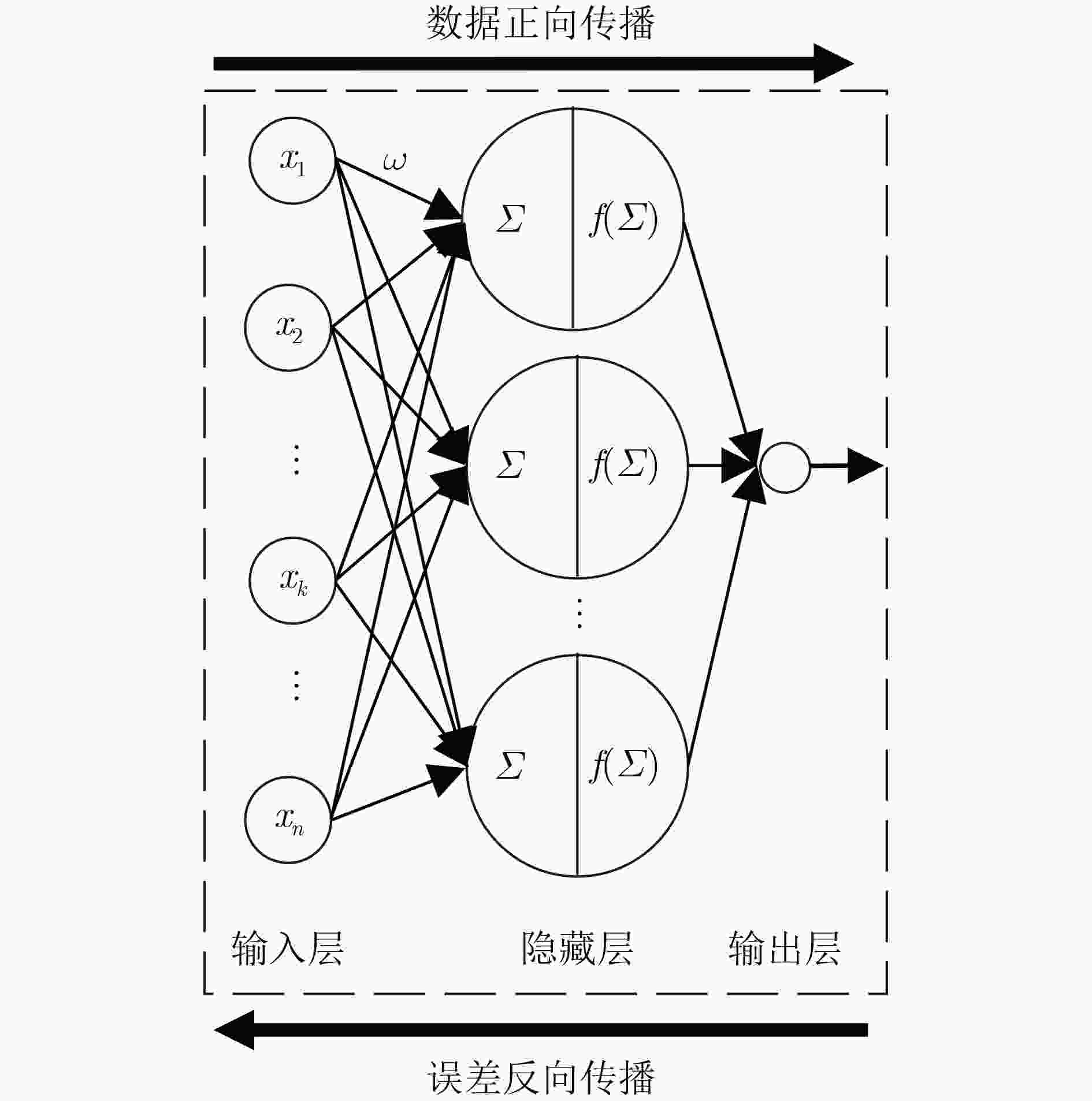
密度(g/cm3) 介电常数 损耗正切角 样本编号 2.4 6.246 0.0011 76315 表 4 神经网络模型结构参数
名称 参数 输入层 8 输出层 1 误差函数 Mean-Square Error (MSE) 优化函数 Root Mean Square Prop(RMSProp)[19] 表 5 神经网络结构
隐藏层 神经元个数 激活函数 1 64 ReLU 2 64 ReLU 3 64 Sigmoid 4 64 Sigmoid 5 32 ReLU 6 32 ReLU 7 16 ReLU 8 16 ReLU -
[1] YANG Wei and LIN Yangting. New lunar samples returned by Chang’E-5: Opportunities for new discoveries and international collaboration[J]. The Innovation, 2021, 2(1): 100070. doi: 10.1016/j.xinn.2020.100070 [2] ZHANG Jinhai, ZHOU Bin, LIN Yangting, et al. Lunar regolith and substructure at Chang’E-4 landing site in South Pole–Aitken basin[J]. Nature Astronomy, 2021, 5(1): 25–30. doi: 10.1038/s41550-020-1197-x [3] ZHANG Jinhai, YANG Wei, HU Sen, et al. Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(17): 5342–5347. doi: 10.1073/pnas.1503082112 [4] ZHANG Ling, ZENG Zhaofa, LI Jing, et al. A story of regolith told by lunar penetrating radar[J]. Icarus, 2019, 321: 148–160. doi: 10.1016/j.icarus.2018.11.006 [5] TRAVASSOS X L, AVILA S L, and IDA N. Artificial neural networks and machine learning techniques applied to ground penetrating radar: A review[J]. Applied Computing and Informatics, 2020, 17(2): 296–308. doi: 10.1016/j.aci.2018.10.001 [6] 侯斐斐, 施荣华, 雷文太, 等. 面向探地雷达B-scan图像的目标检测算法综述[J]. 电子与信息学报, 2020, 42(1): 191–200. doi: 10.11999/JEIT190680HOU Feifei, SHI Ronghua, LEI Wentai, et al. A review of target detection algorithm for GPR B-scan processing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 191–200. doi: 10.11999/JEIT190680 [7] 王建, 袁宵, 李禹, 等. 利用互相关和Hough变换快速检测探地雷达目标[J]. 电子与信息学报, 2013, 35(5): 1156–1162. doi: 10.3724/SP.J.1146.2012.01134WANG Jian, YUAN Xiao, LI Yu, et al. Fast detection of ground penetrating radar objects based on cross correlation and Hough transform[J]. Journal of Electronics &Information Technology, 2013, 35(5): 1156–1162. doi: 10.3724/SP.J.1146.2012.01134 [8] GAO Jie, YUAN Dongdong, TONG Zheng, et al. Autonomous pavement distress detection using ground penetrating radar and region-based deep learning[J]. Measurement, 2020, 164: 108077. doi: 10.1016/j.measurement.2020.108077 [9] LI Shuwei, GU Xingyu, XU Xiangrong, et al. Detection of concealed cracks from ground penetrating radar images based on deep learning algorithm[J]. Construction and Building Materials, 2021, 273: 121949. doi: 10.1016/j.conbuildmat.2020.121949 [10] KHUDOYAROV S, KIM N, and LEE J J. Three-dimensional convolutional neural network–based underground object classification using three-dimensional ground penetrating radar data[J]. Structural Health Monitoring, 2020, 19(6): 1884–1893. doi: 10.1177/1475921720902700 [11] LIU T, KLOTZSCHE A, PONDKULE M, et al. Estimation of subsurface cylindrical object properties from GPR full-waveform inversion[C]. The 2017 9th International Workshop on Advanced Ground Penetrating Radar, Edinburgh, UK, 2017: 1–4. [12] GIANNAKIS I, GIANNOPOULOS A, and WARREN C. A machine learning scheme for estimating the diameter of reinforcing bars using ground penetrating radar[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(3): 461–465. doi: 10.1109/LGRS.2020.2977505 [13] CARLSON I C and WALTON W J A. Apollo-14 rock samples[R]. JSC 14240, 1978. [14] GIANNOPOULOS A. Modelling ground penetrating radar by GprMax[J]. Construction and Building Materials, 2005, 19(10): 755–762. doi: 10.1016/j.conbuildmat.2005.06.007 [15] DENG Caixia, WANG Guibin, and YANG Xinrui. Image edge detection algorithm based on improved canny operator[C]. 2013 International Conference on Wavelet Analysis and Pattern Recognition, Tianjin, China, 2013: 168–172. [16] GOLD T, BILSON E, and BARON R L. Electrical properties of Apollo 17 rock and soil samples and a summary of the electrical properties of lunar material at 450 MHz frequency[C]. The 7th Lunar Science Conference, New York, USA, 1976: 2593–2603. [17] WOLD S, ESBENSEN K, and GELADI P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1/3): 37–52. doi: 10.1016/0169-7439(87)80084-9 [18] PENNINGTON J, SCHOENHOLZ S S, and GANGULI S. Resurrecting the sigmoid in deep learning through dynamical isometry: Theory and practice[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 4788–4798. [19] HINTON G, SRIVASTAVA N, and SWERSKY K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent[J]. Cited on, 2012, 14(8): 2. [20] FIELD A. Logistic Regression[M]. FIELD A. Discovering Statistics Using SPSS. London: SAGE Publications Ltd, 2009: 264–315. -






 下载:
下载:
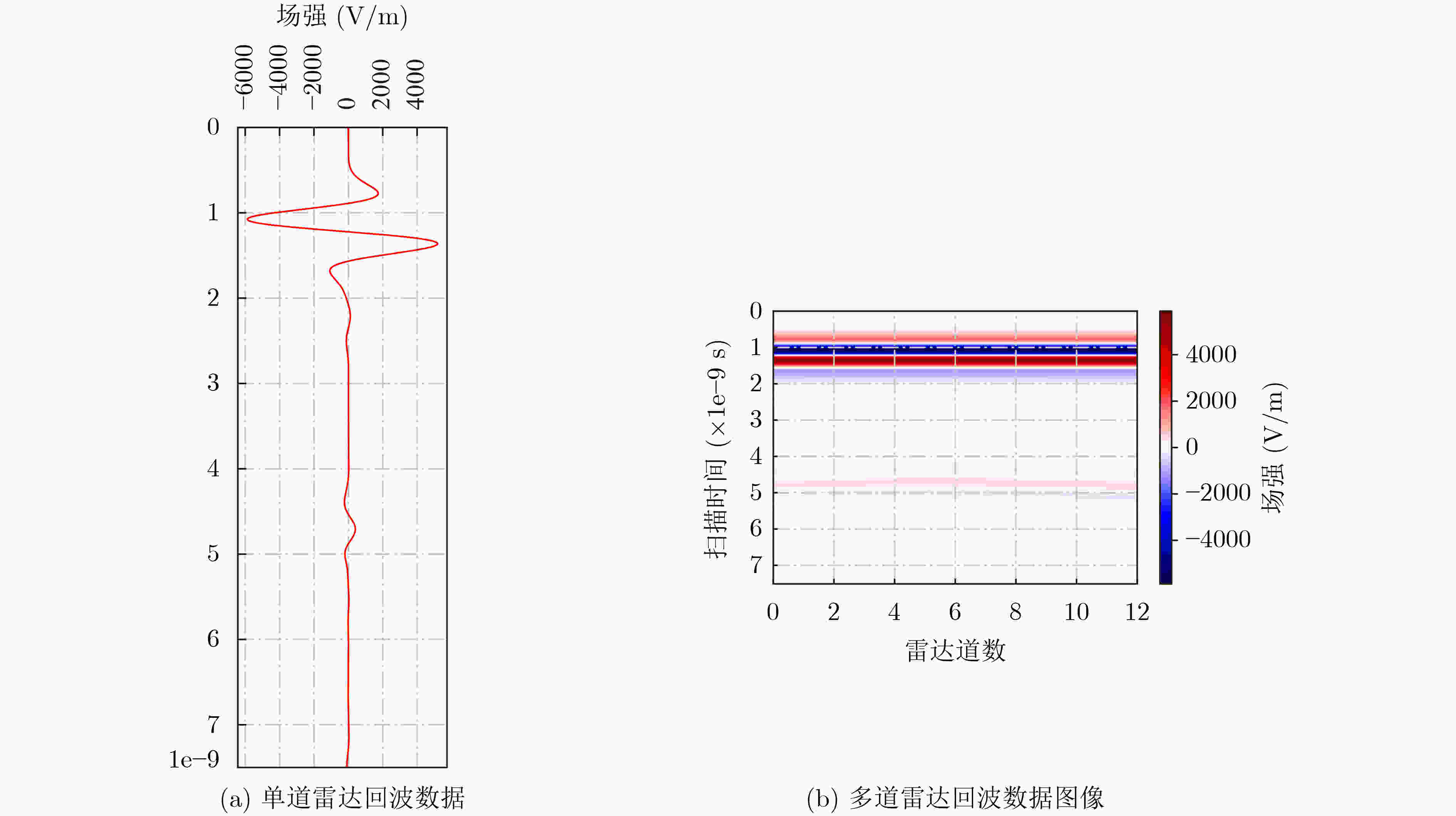
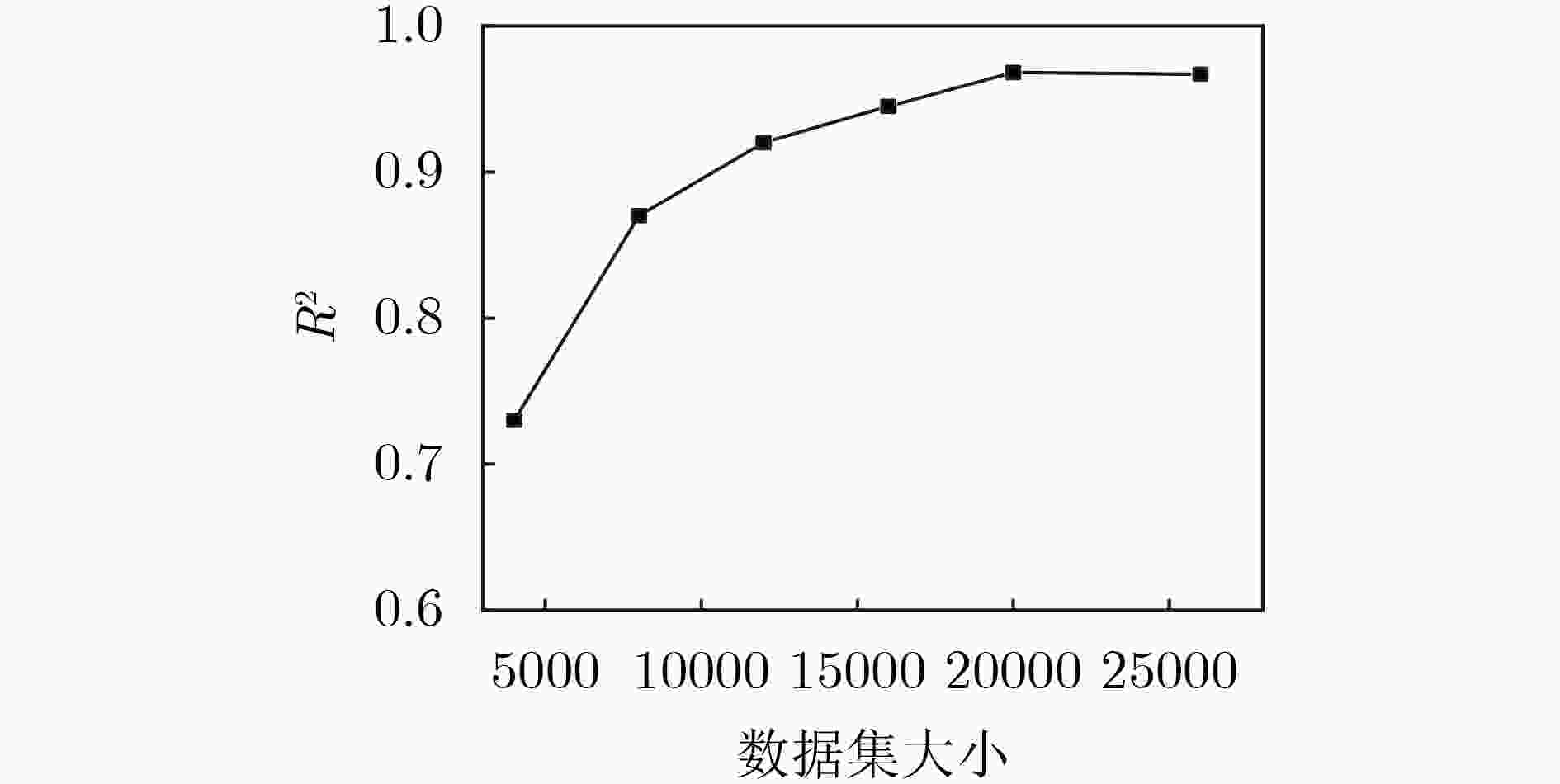

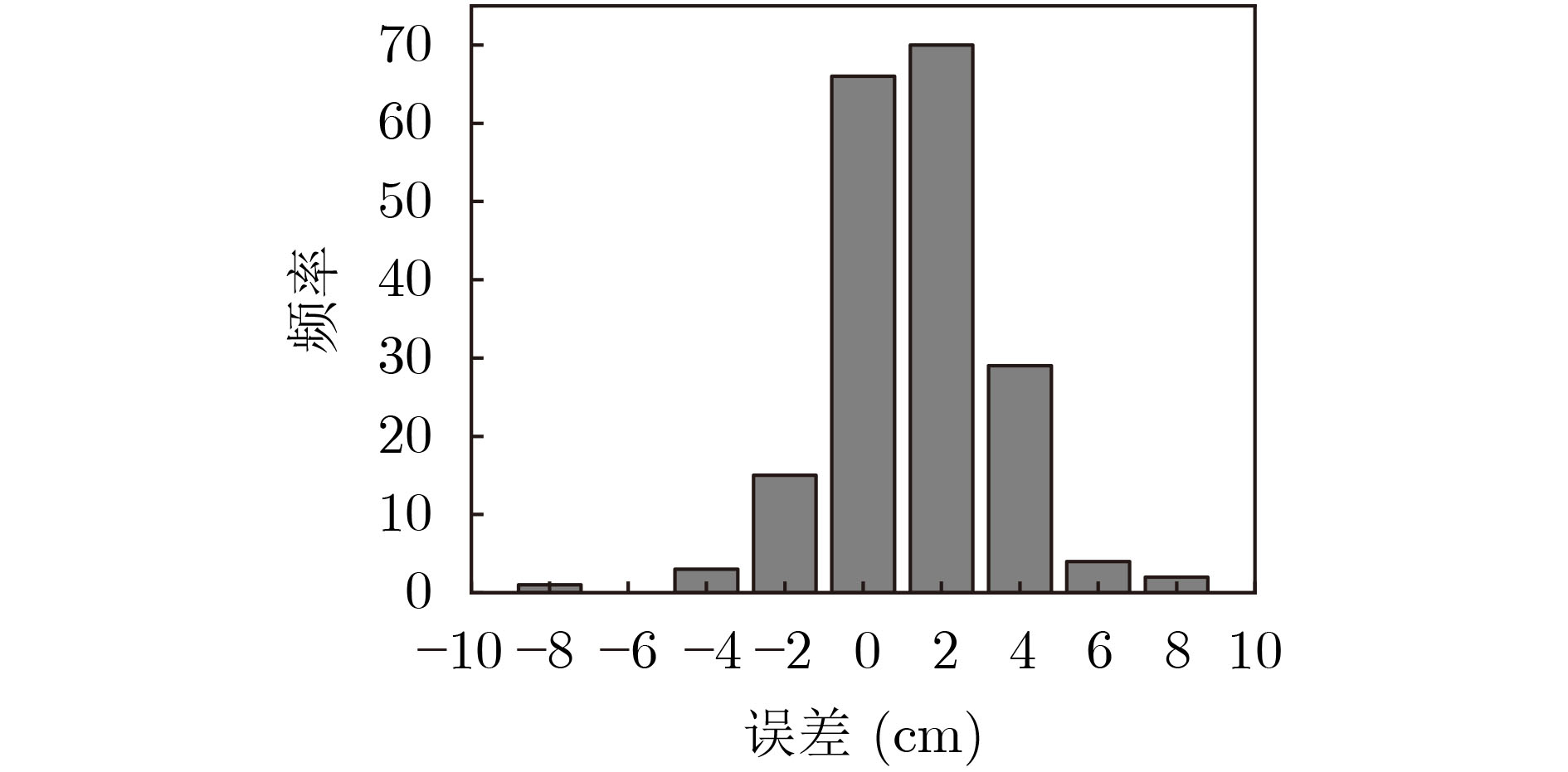
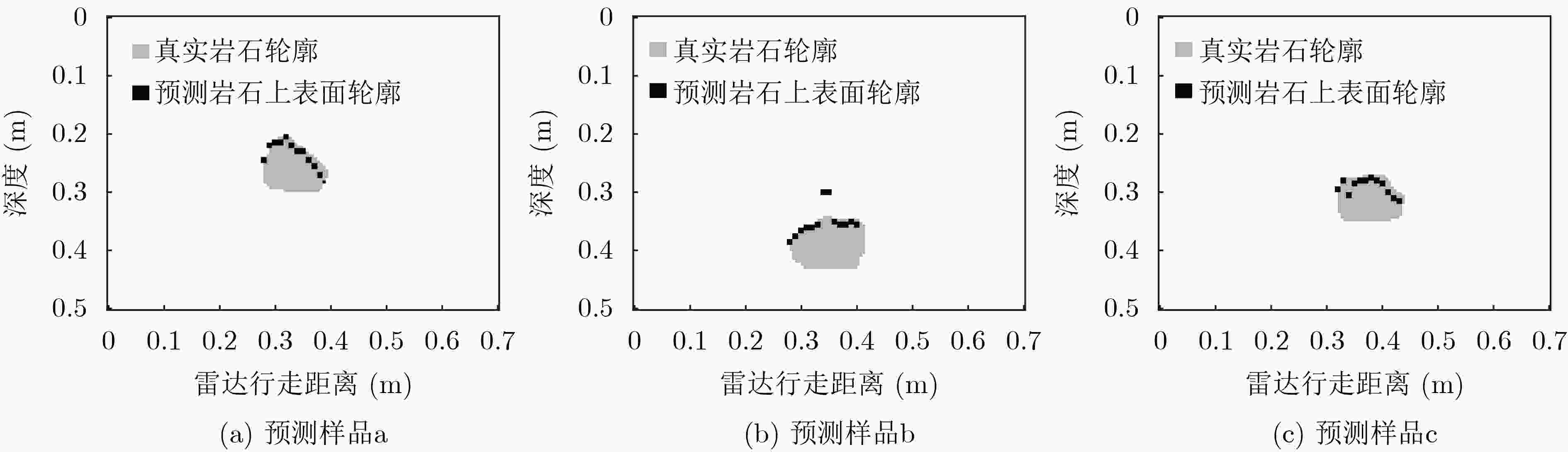
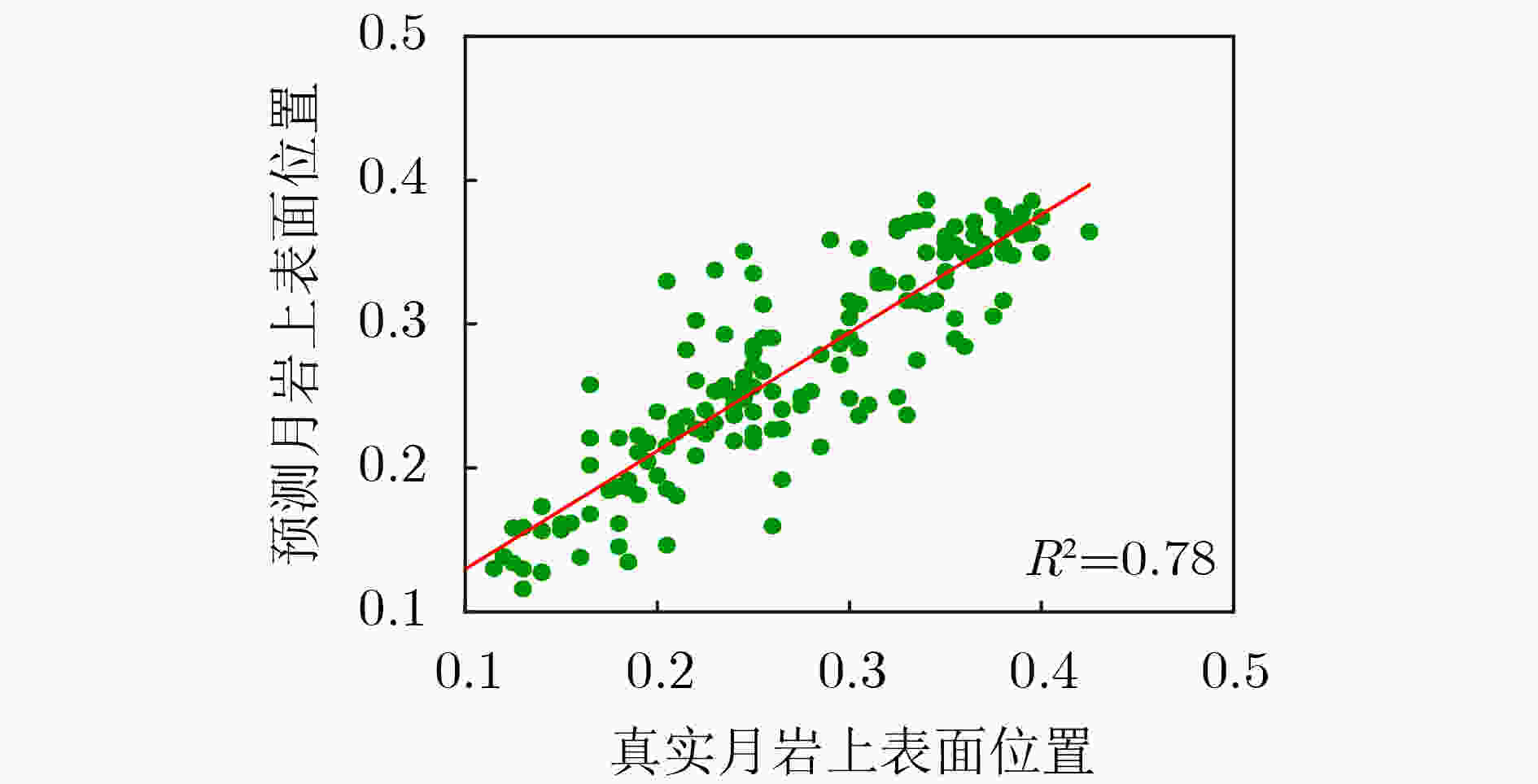

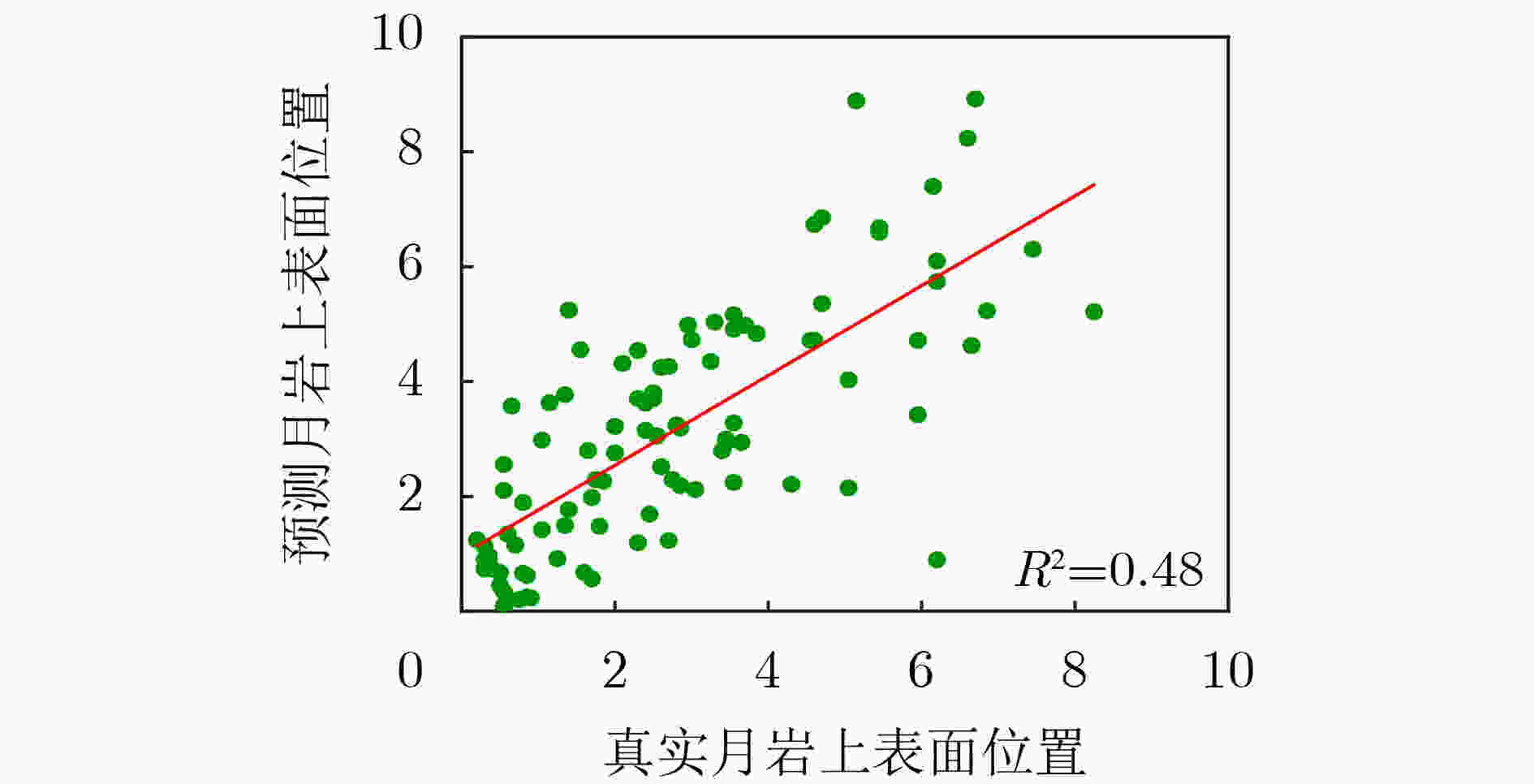


 下载:
下载:
