融合多属性决策和深度Q值网络的反导火力分配方法

谢俊伟; 方峰; 彭冬亮; 任金磊; 王昌平

doi:10.11999/JEIT211136

融合多属性决策和深度Q值网络的反导火力分配方法

doi: 10.11999/JEIT211136

1.
杭州电子科技大学自动化学院杭州 310018
2.
中国运载火箭技术研究院北京 100076

基金项目: 国家自然科学基金 (61673146)，浙江省属高校科研基金(GK209907299001-021)

详细信息

作者简介:
谢俊伟：男，博士生，研究方向为智能决策与控制

方峰：男，讲师，博士，研究方向为飞行器协同制导与控制、智能决策

彭冬亮：男，教授，博士，博士生导师，研究方向为信息融合、检测与估计

任金磊：男，工程师，硕士，研究方向为飞行器设计、弹道导航制导控制、智能控制

王昌平：男，硕士生，研究方向为导弹协同制导

通讯作者:
方峰　fangf@hdu.edu.cn

中图分类号: TP183; TJ761.7
计量
- 文章访问数: 1444
- HTML全文浏览量: 737
- PDF下载量: 161
- 被引次数: 4
出版历程
- 收稿日期: 2021-10-15
- 修回日期: 2022-01-10
- 录用日期: 2022-01-14
- 网络出版日期: 2022-02-02
- 刊出日期: 2022-11-14

Weapon-Target Assignment Optimization Based on Multi-attribute Decision-making and Deep Q-Network for Missile Defense System

1.
School of Automation, Hangzhou Dianzi University, Hangzhou 310018, China
2.
China Academy of Launch Vehicle Technology, Beijing 100076, China

Funds: The National Natural Science Foundation of China(61673146), Zhejiang Provincial University Research Foundation (GK209907299001-021)

摘要

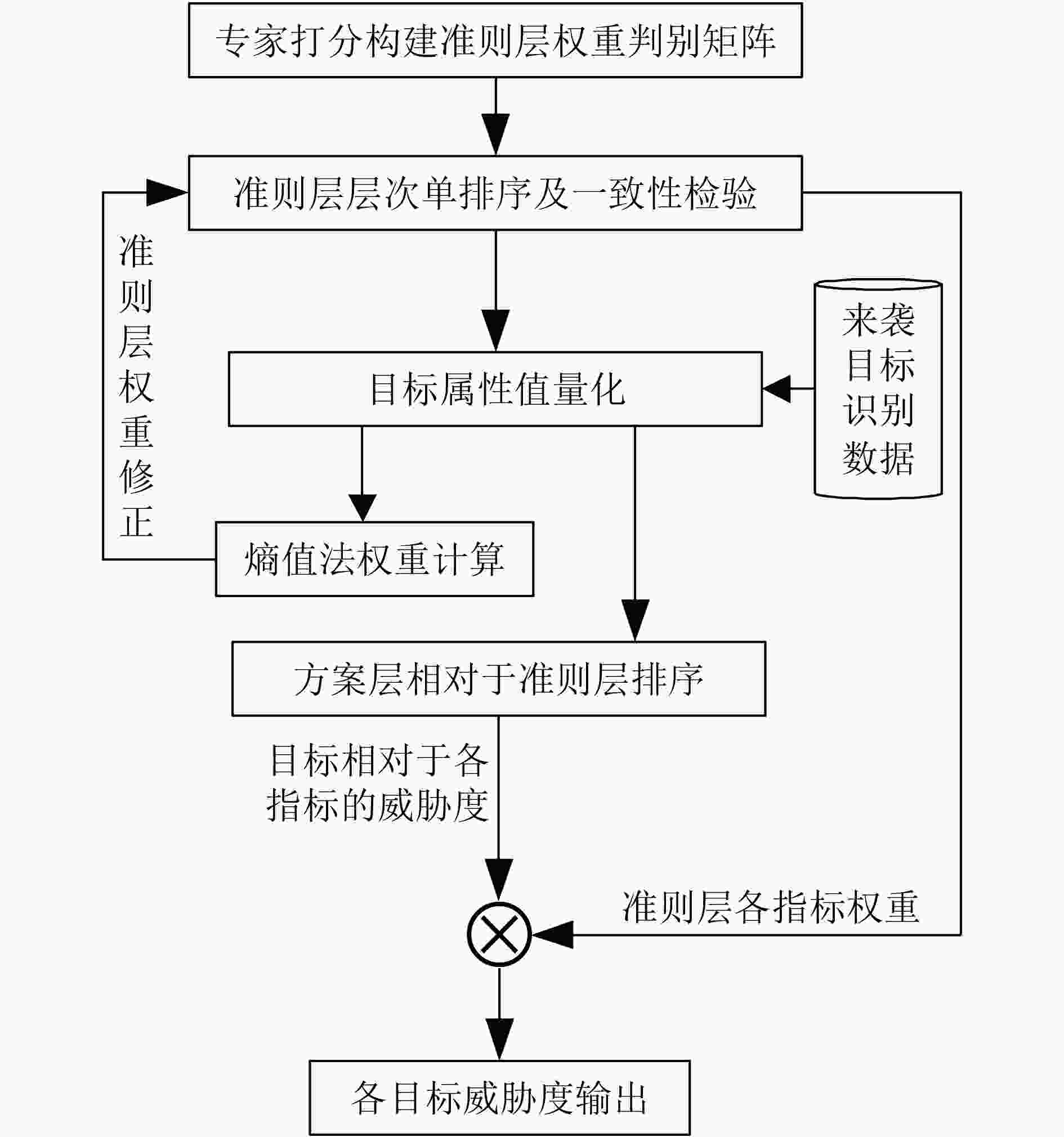
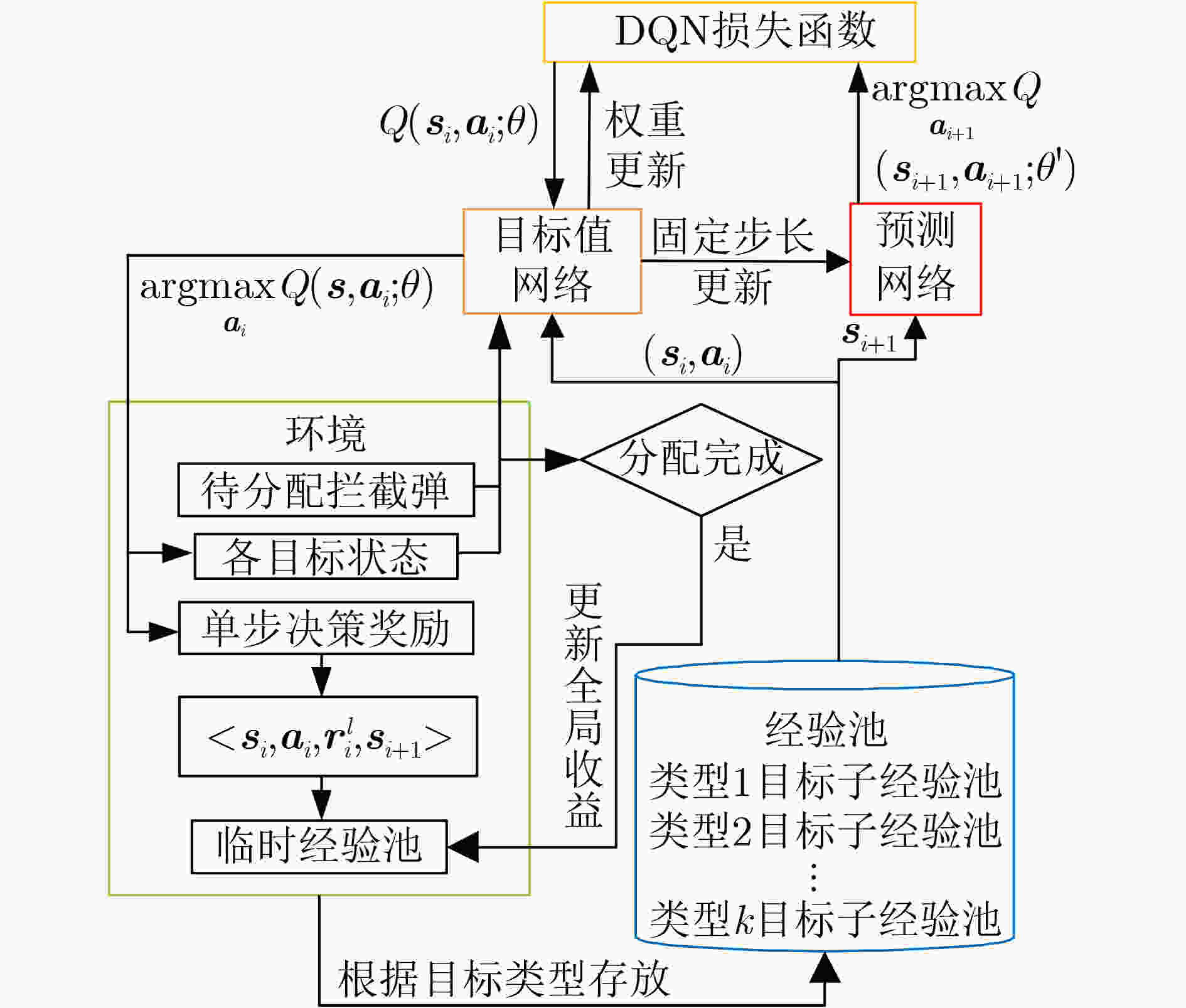
摘要: 针对中大规模武器-目标分配(WTA)决策空间复杂度高、求解效率低的问题，该文提出一种基于多属性决策和深度Q网络(DQN)的WTA优化方法。建立基于层次分析法(AHP)的导弹威胁评估模型，引入熵值法表征目标属性差异，提升威胁评估客观性。根据最大毁伤概率准则，建立基于DQN的WTA分段决策模型，引入经验池均匀采样策略，确保各类目标分配经验的等概率抽取；设计综合局部和全局收益的奖励函数，兼顾DQN火力分配模型的训练效率和决策准确性。仿真结果表明，相较于传统启发式方法，该方法具备在线快速求解大规模WTA问题的优势，且对于WTA场景要素变化具有较好的鲁棒性。
- 火力分配 /
- 深度Q网络 /
- 威胁评估 /
- 改进层次分析法
Abstract: In a large-scale Weapon-Target Assignment (WTA) problem, the explored solution space becomes enormous due to the curse of dimensionality, and it causes low-efficiency in searching optimization solution. For solving this problem effectively, a WTA optimization approach based on multi-attribute decision-making and Deep Q-Network (DQN) is proposed. Firstly, a threat-assessment model for attacking missiles is built based on the approach of Analytic Hierarchy Process (AHP). Meanwhile, an entropy method, used for evaluating the differences of target attributes, is introduced, to increase objective in computing threat-assessment results. Then, an assignment criterion of maximum intercept probability is designed based on assess results, and a multi-steps WTA decision model is built in DQN frame. A uniform experience sampling strategy is designed, making sure that each target type of assignment experience has the same probability to be selected. Furthermore, for balancing the DQN convergence speed and global optimum, a reward function that combines local and global rewards is designed. Lastly, simulation results shows that the proposed WTA approach has the advantage in solving large-scale WTA problem fast and effectively, compared with the general heuristic approach. Also, it presents the robust performance for WTA scenario elements variation.
- Weapon Target Assignment(WTA) /
- Deep Q Network(DQN) /
- Threat assessment /
- Improved Analytic Hierarchy Process(AHP)

HTML全文

1. 引言

机动平台大斜视合成孔径雷达(Synthetic Aperture Radar, SAR)成像系统能够进一步增强导弹、战机以及无人机的战场侦察、精确打击和自我生存能力，相关的成像方法受到了广泛关注^[1-4]。

机载SAR易受气流扰动，由于惯导设备精度有限，基于回波数据的自聚焦方法通常是SAR成像过程中必不可少的环节。对于机动平台大斜视SAR成像，大斜视角和空间3维加速度的存在使运动误差具有明显的2维空变性，极大地增加了自聚焦的难度。常规的相位梯度自聚焦(Phase Gradient Autofocus, PGA)^[5]、最小熵(Minimum Entropy Analysis, MEA)^[6]等自聚焦方法及其改进算法^[7,8]，在非空变的包络误差校正和方位相位补偿等方面有显著效果。当运动误差同时存在距离和方位2维空变时，文献[9]推导了混合坐标系下图像域和方位时域相位的近似傅里叶变换关系，采用高斯拟牛顿的方法估计3维的运动误差轨迹，并采用时域算法进行成像处理。文献[10]在快速分解后向投影(Fast Factorized Back Projection, FFBP)算法框架下，基于最大对比度准则对双基地SAR成像模式下的双机3维运动误差轨迹进行迭代估计。文献[11]在稀疏自聚焦框架下，提出了一种误差轨迹重建方法，但该方法需要在时域建立稀疏表示矩阵，内存占用极大，仅能用于小场景成像。为实现大场景成像，文献[12]将近似观测算子模型引入稀疏自聚焦框架，极大地降低了内存占用，使稀疏自聚焦方法可以用于大场景成像，但其无法估计和补偿2维空变的运动误差。文献[13]在近似观测算子模型下进一步扩展了稀疏自聚焦框架，提出了一种运动误差幅相联合补偿算法，能够实现空变运动误差的估计与补偿，但巨大的运算量限制了其应用。3维运动误差轨迹的估计需要建立图像域和方位时域相位历程的映射关系，当平台存在较大的斜视角和加速度时，运动误差中的线性分量将极大地影响3维运动误差的估计精度。

常规的PGA和MEA等自聚焦方法仅能用于全采样数据下的误差相位估计和补偿，而稀疏自聚焦方法可以同时用于全采样和欠采样数据下的误差相位估计与补偿，具有更高的精度和更大的适用范围^[14]。本文在稀疏自聚焦框架下，提出了适用于机动平台大斜视SAR聚束成像的2维空变运动误差估计与补偿方法。该方法基于Keystone变换和频域相位滤波法^[15,16]构建了一种能够校正成像参数空变性的频域近似观测算子，并对距离方位解耦后的方位时域运动误差进行高阶多项式建模，通过多个子区域的非空变误差相位估计空变的运动误差多项式系数，最后通过修正频域近似观测算子中的相位滤波系数，实现了全采样和欠采样数据下的2维空变运动误差的补偿。

本文的后续结构安排如下：第2节介绍机动平台大斜视SAR频域近似观测算子构造方法；第3 节详细论述距离和方位2维空变相位误差的估计与补偿方法，并进行运算量分析；第4节给出真实SAR场景回波反演数据的成像结果，验证了本文方法的有效性；第5节对全文进行总结。

2. 近似观测模型

加速度和大斜视角的存在使机动平台大斜视SAR的成像参数具有明显2维空变性，为实现距离方位解耦、多普勒谱去混叠以及空变线性距离徙动的校正，采用文献[4]中的方法对回波信号先后进行距离走动校正、去加速度处理和方位向Keystone变换，可得距离徙动校正和距离压缩后的信号为

$\begin{split} s{s_{{\rm{key}}}}\left( {{t_{\rm{r}}},{t_{\rm{a}}};{R_{\rm{f}}},{t_{\rm{n}}}} \right) =\,& {\rm{sinc}}\left( {{t_{\rm{r}}} - 2{R_{\rm{f}}}/{\rm{c}}} \right)\\ & \cdot \exp \left( {{\rm{j}}{\phi _{\rm{a}}}\left( {{t_{\rm{a}}};{R_{\rm{f}}},{t_{\rm{n}}}} \right)} \right) \end{split}$

(1)

其中， ${t_{\rm{r}}}$ 表示距离时间， ${t_{\rm{a}}}$ 为方位时间， ${R_{\rm{f}}}$ 为点目标距离压缩后的斜距， ${t_{\rm{n}}}$ 表示点目标的方位向位置，c为光速， ${\phi _{\rm{a}}}\left( {{t_{\rm{a}}};{R_{\rm{f}}},{t_{\rm{n}}}} \right)$ 为方位时域调制相位，表示为^[4]

${\phi _{\rm{a}}}\left( {{t_{\rm{a}}};{R_{\rm{f}}},{t_{\rm{n}}}} \right) = \sum\limits_{i = 0}^{\rm{4}} {{g_i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)t_{\rm{a}}^i}$

(2)

其中， ${g_i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)$ 表示第i阶泰勒级数展开系数，具体求解方法见文献[4]。为便于校正多普勒参数的方位空变性，将 ${g_i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)$ 在 ${t_{\rm{n}}} = 0$ 处进行如式(3)所示的泰勒级数展开

$\left. \begin{aligned} & {g_1}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right) = {g_{10}}({R_{\rm{f}}}) + {g_{11}}({R_{\rm{f}}}){t_{\rm{n}}} + {g_{1{\rm{2}}}}({R_{\rm{f}}})t_{\rm{n}}^2\\ & {g_{\rm{2}}}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right) = {g_{{\rm{2}}0}}({R_{\rm{f}}}) + {g_{{\rm{2}}1}}({R_{\rm{f}}}){t_{\rm{n}}} + {g_{{\rm{22}}}}({R_{\rm{f}}})t_{\rm{n}}^2\\ & {g_{\rm{3}}}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right) = {g_{{\rm{3}}0}}({R_{\rm{f}}}) + {g_{{\rm{3}}1}}({R_{\rm{f}}}){t_{\rm{n}}}\\ & {g_{\rm{4}}}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right) = {g_{{\rm{4}}0}}({R_{\rm{f}}}) \end{aligned} \right\}$

(3)

其中， ${g_{in}}$ 表示 ${g_i}$ 的第n阶展开系数。

在方位压缩处理中，本文基于频域相位滤波^[15,16]的思想校正空变的多普勒参数。首先，采用式(4)去除距离依赖的多普勒中心

${H_3}\left( {{R_{\rm{f}}},{t_{\rm{a}}}} \right) = \exp \left( { - {\rm{j}}{g_{10}}({R_{\rm{f}}}){t_{\rm{a}}}} \right)$

(4)

然后，采用级数反演法变换到方位频域得

$s{S_{{\rm{key}}}}\left( {{R_{\rm{f}}},{f_{\rm{a}}};{t_{\rm{n}}}} \right) = \exp \left( {{\rm{j}}\left( {\sum\limits_{i = 0}^4 {{\varphi _i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)f_{\rm{a}}^i} } \right)} \right)$

(5)

其中， ${f_{\rm{a}}}$ 表示方位频率， ${\varphi _i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)$ 表示第i阶方位频率调制系数，其距离依赖性可通过逐距离单元的方位压缩去除。因此，为便于推导，将 ${\varphi _i}\left( {{R_{\rm{f}}},{t_{\rm{n}}}} \right)$ 简记为 ${\varphi _i}\left( {{t_{\rm{n}}}} \right)$ ，并将 ${\varphi _i}\left( {{t_{\rm{n}}}} \right)$ 在 ${t_{\rm{n}}} = 0$ 处进行如式(6)所示的泰勒级数展开得

$\left. \begin{aligned} &{\varphi _1}\left( {{t_{\rm{n}}}} \right) = {\varphi _{11}}{t_n} + {\varphi _{12}}t_{\rm{n}}^{\rm{2}}\\ &{\varphi _2}\left( {{t_{\rm{n}}}} \right) = {\varphi _{20}} + {\varphi _{21}}{t_{\rm{n}}} + {\varphi _{22}}t_{\rm{n}}^2\\ &{\varphi _3}\left( {{t_{\rm{n}}}} \right) = {\varphi _{30}} + {\varphi _{31}}{t_{\rm{n}}}\\ &{\varphi _4}\left( {{t_{\rm{n}}}} \right) = {\varphi _{40}} \end{aligned} \right\}$

(6)

其中， ${\varphi _{in}}$ 表示 ${\varphi _i}$ 的第n阶展开系数。

为去除多普勒调频率的1阶和2阶方位空变性，构造如式(7)所示的频域相位滤波函数

${H_4}\left( {{R_{\rm{f}}},{f_{\rm{a}}}} \right) = \exp \left( {{\rm{j}}\left( {\left( {{s_3} - {\varphi _{30}}} \right)f_{\rm{a}}^3 + \left( {{s_4} - {\varphi _{40}}} \right)f_{\rm{a}}^4} \right)} \right)$

(7)

其中频域扰动系数 ${s_3}$ 和 ${s_4}$ 分别为

$\left. \begin{aligned} & {s_3} = \frac{{f_{\rm{c}}^2{\varphi _{20}}{\varphi _{21}}}}{{{\rm{3\pi }}{\varphi _{11}}}}\\ & {s_4} = \frac{{f_{\rm{c}}^3{\varphi _{20}}\left( {3\varphi _{11}^2{\varphi _{31}} - 2{\varphi _{11}}{\varphi _{20}}{\varphi _{22}} - {\varphi _{11}}\varphi _{21}^2 + 2{\varphi _{12}}{\varphi _{20}}\varphi {}_{21}} \right)}}{{6{\rm{\pi }}\varphi _{11}^3}} \end{aligned} \right\}$

(8)

频域相位滤波后，构造如式(9)所示的方位时域Deramp函数

$\begin{split} {H_5}\left( {{R_{\rm{f}}},{t_{\rm{a}}}} \right) =\,& \exp \Biggr( - {\rm{j}}\Biggr( \frac{{{\rm{\pi c}}}}{{4{f_{\rm{c}}}{\varphi _{20}}}}t_{\rm{a}}^2 + \frac{{{{\rm{\pi }}^3}{\rm{c}}{s_3}}}{{f_{\rm{c}}^3\varphi _{20}^3}}t_{\rm{a}}^3 \\ & \left.\left.+ \frac{{3{{\rm{\pi }}^4}{\rm{c}}\left( {\varphi _{11}^2{s_4} - f_{\rm{c}}^3\varphi _{20}^{}\varphi _{21}^2} \right)}}{{2f_{\rm{c}}^4\varphi _{20}^4\varphi _{11}^2}}t_{\rm{a}}^4 \right) \right) \end{split}$

(9)

Deramp处理后，通过方位快速傅里叶变换(Fast Fourier Transform, FFT)即可实现方位压缩。最终，机动平台大斜SAR频域成像处理流程如图1所示，其中滤波函数 ${H_1}$ 和 ${H_2}$ 的具体形式见文献[4]。

图 1 机动平台大斜SAR频域成像处理流程

下载: 全尺寸图片幻灯片

设接收机收到的原始2维回波数据为 ${S} \in {C^{M \times N}}$ , M和N分别表示方位和距离向上的采样点数，则距离方位解耦后的距离压缩回波可以表示为

${{S}_{{\rm{rc}}}} = {F}_{\rm{r}}^{\rm{H}}\left( {{C_{{\rm{key}}}}\left( {{{F}_{\rm{r}}}\left( {{L} \odot {S}} \right) \odot {H}_1^{}} \right) \odot {{H}_2}} \right) \odot {{H}_3}$

(10)

其中，“ $\odot$ ”为Hadamard积，表示矩阵点乘运算， ${{H}_i}$ 表示由相位滤波因子 ${{H}_i}$ 生成的相位滤波矩阵， ${C_{{\rm{key}}}}$ 表示Keystone变换处理， ${{F}_{\rm{r}}}$ 和 ${F}_{\rm{r}}^{\rm{H}}$ 分别表示距离向FFT和逆FFT(Inverse FFT, IFFT)操作。L是一个仅包含0和1的降采样矩阵，设 ${\xi _{\rm{a}}}$ 表示方位向上的降采样率， ${\xi _{\rm{r}}}$ 表示距离向上的降采样率，则L共有 $N{\xi _{\rm{a}}}$ 个非0列，每一列有 $M{\xi _{\rm{r}}}$ 个1。

设成像场景的2维散射矩阵为 ${G}$ ，基于距离压缩回波的成像算子可表示为

${G} = {\varGamma }\left( {{{S}_{{\rm{rc}}}}} \right) = {{F}_{\rm{a}}}\left( {{F}_{\rm{a}}^{\rm{H}}\left( {{{F}_{\rm{a}}}\left( {{{S}_{{\rm{rc}}}}} \right) \odot {{H}_4}} \right) \odot {{H}_5}} \right)$

(11)

其中， ${{F}_{\rm{a}}}$ 和 ${F}_{\rm{a}}^{\rm{H}}$ 分别表示方位向FFT和IFFT操作。

式(11)是一个仅包含矩阵乘法和矩阵点乘的线性运算。因此，在已知 ${G}$ 的情况下，可通过 ${\varGamma }\left( \cdot \right)$ 的逆运算 ${{\varGamma }^{ - 1}}\left( \cdot \right)$ 来生成距离压缩回波 ${{S}_{{\rm{rc}}}}$ ，即

${{S}_{{\rm{rc}}}} = {{\varGamma }^{ - 1}}\left( {G} \right) = {F}_{\rm{a}}^{\rm{H}}\left( {{{F}_{\rm{a}}}\left( {{F}_{\rm{a}}^{\rm{H}}{G} \odot {H}_5^*} \right) \odot {H}_4^*} \right)$

(12)

其中，“ $*$ ”表示矩阵共轭，由于 ${G}$ 是匹配滤波成像结果，并非场景的真实散射系数，因此 ${{\varGamma }^{ - 1}}\left( \cdot \right)$ 称为近似观测。

3. 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

为估计非空变的运动误差相位并实现场景的粗聚焦，假设SAR系统仅存在非空变的相位误差 ${\varPhi }$ ，表示为

${\varPhi } = {\rm{diag}}\left( {{{\rm{e}}^{{\rm{j}}\phi \left( 1 \right)}},{{\rm{e}}^{{\rm{j}}\phi \left( 2 \right)}}, ··· ,{{\rm{e}}^{{\rm{j}}\phi \left( M \right)}}} \right)$

(13)

其中， ${X}{\rm{ = diag}}\left( {v} \right)$ 表示以向量v的元素作为矩阵X的主对角线元素。

则基于近似观测的稀疏自聚焦模型可表示为

$\left\langle {{G},{\varPhi }} \right\rangle = \arg \mathop {\min }\limits_{{G},{\varPhi }} \left\{ {\frac{1}{2}\left\| {{{S}_{{\rm{rc}}}} - {\varPhi }{{{\varGamma}} ^{ - 1}}\left( {G} \right)} \right\|_{\rm{F}}^2 + \lambda {{\left\| {G} \right\|}_1}} \right\}$

(14)

其中， $\left\| {X} \right\|_{\rm{F}}^{2}$ 表示矩阵 ${X}$ 所有元素模的平方之和， ${\left\| {X} \right\|_1}$ 表示矩阵 ${X}$ 所有元素模的和， $\lambda$ 表示正则化参数。

式(14)中的稀疏优化模型可以采用基于两步优化和迭代软阈值(Iterative Shrinkage-Thresholding Algorithm, ISTA)的稀疏自聚焦方法^[12]进行求解。

3.2 空变的运动误差模型

在距离向处理中，Keystone变换去除了包络幅度误差中线性分量对距离徙动校正的影响，通常情况下，残余的非线性包络幅度误差对距离徙动校正的影响可以忽略。本文重点研究方位压缩过程中，距离空变和方位空变的相位误差估计与校正。

采用稀疏自聚焦方法估计出全局非空变误差相位 ${{\varPhi }_{{\rm{inv}}}}$ 后，可以获取成像场景的粗聚焦图像 ${{G}_{\rm{c}}} =$ $\varGamma \left( {{\varPhi }_{{\rm{inv}}}^*{{S}_{{\rm{rc}}}}} \right)$ 。在 ${{G}_{\rm{c}}}$ 中，残余误差相位是沿距离和方位向缓慢空变的，但在一个子区域中，残余误差相位可以看作空不变的。采用稀疏自聚焦方法估计子区域的局部相位误差时，所选择的子区域应具有较高的对比度且在距离和方位向上有较大的分散性^[9]。对于任一子图像 ${{G}_{{\rm{c}}\_{\rm{sub}}}}$ ，首先恢复其距离压缩回波 ${{S}_{{\rm{rc}}\_{\rm{sub}}}}{\rm{ = }}{{{\varGamma}} ^{ - 1}}\left( {{{G}_{{\rm{c}}\_{\rm{sub}}}}} \right)$ ，然后采用稀疏自聚焦方法估计子图像 ${{G}_{{\rm{c}}\_{\rm{sub}}}}$ 的残余误差相位 ${{\varPhi }_{{\rm{c}}\_{\rm{sub}}}}$ 。基于不同子区域的局部相位误差，可采用最小二乘法实现空变残余误差相位的估计与补偿。

本文采用的2维空变误差校正方法，是通过修正所构建的频域近似观测算子中的滤波系数来实现的。在所构建的频域近似观测算子中，斜距模型为文献[4]中的4阶多项式模型，观察式(3)中多普勒参数的空变展开系数可以发现，在频域相位滤波法中，回波的方位时域调制相位需考虑多普勒中心和调频率的2阶方位空变性，3阶多普勒参数的1阶方位空变性。为便于在频域相位滤波法中校正空变的运动误差，运动误差的多项式阶数应与斜距模型一致。因此，本文将距离压缩回波中的残余空变误差相位在距离和方位向近似为如下所示的4阶多项式模型

$\begin{split} \Delta \phi \left( {\Delta R,{t_{\rm{n}}}} \right) =\,& a\left( {\Delta R,{t_{\rm{n}}}} \right){t_{\rm{a}}} + b\left( {\Delta R,{t_{\rm{n}}}} \right)t_{\rm{a}}^{\rm{2}} \\ & + c\left( {\Delta {R_0},{t_{\rm{n}}}} \right)t_a^3 + {d_0}\left( {\Delta R} \right)t_{\rm{a}}^4 \end{split}$

(15)

其中， $\Delta R = {R_{\rm{f}}} - {R_{{\rm{ref}}}}$ , ${R_{{\rm{ref}}}}$ 表示方位0时刻的场景中心点斜距， $a\left( {\Delta R,{t_{\rm{n}}}} \right)$ , $b\left( {\Delta R,{t_{\rm{n}}}} \right)$ 和 $c\left( {\Delta R,{t_{\rm{n}}}} \right)$ 分别表示2维空变的多普勒中心，多普勒调频率和3阶多普勒参数， ${d_0}\left( {\Delta R} \right)$ 表示距离依赖的4阶多普勒系数，具体表示为

$\left. \begin{aligned} & b\left( {\Delta R,{t_{\rm{n}}}} \right) = {b_0} + {b_{{\rm{a1}}}}{t_{\rm{n}}} + {b_{{\rm{a}}2}}t_{\rm{n}}^{\rm{2}} + {b_{{\rm{r1}}}}\Delta R + {b_{{\rm{r1}}}}\Delta {R^2}\\ & c\left( {\Delta R,{t_{\rm{n}}}} \right) = {c_0} + {c_{{\rm{a1}}}}{t_{\rm{n}}} + {c_{{\rm{r1}}}}\Delta R\;\\ & {d_0}\left( {\Delta R} \right) = {d_0} + {d_{{\rm{r1}}}}\Delta R \end{aligned} \right\}$

(16)

式(15)中的线性分量 $a\left( {\Delta R,{t_{\rm{n}}}} \right){t_{\rm{a}}}$ 会使聚焦后的方位频域图像产生 ${f_{\rm{a}}} = a\left( {\Delta R,{t_{\rm{n}}}} \right)/\left( {2{\rm{\pi }}} \right)$ 的方位位置偏移，该偏移对方位聚焦质量的影响很小，无需估计。

3.3 空变误差相位的求解与补偿

假设在 ${{G}_{\rm{c}}}$ 中共截取了D个子区域，其中第i个子区域的局部误差相位表示为 ${\phi _{{\rm{sub}}\_i}}$ 。采用最小二乘法可以对其进行多项式拟合，则子区域i的4阶多项式拟合系数表示为

$\begin{split} {{u}_{{\rm{sub}}\_i}} =\,& \left[ {{{{\textit{1}}}},{{t}_{\rm{a}}},{t}_{\rm{a}}^2,{t}_{\rm{a}}^{\rm{3}},{t}_{\rm{a}}^{\rm{4}}} \right]_{M \times 4}^{ - 1}\\ & \cdot \left[ {{\phi _{{\rm{sub}}\_i}}\left( 1 \right),{\phi _{{\rm{sub}}\_i}}\left( 2 \right)···,{\phi _{{\rm{sub}}\_i}}\left( M \right)} \right]_{M \times 1}^{\rm{T}}\\ \end{split}$

(17)

其中，1表示含有M个元素的全1列向量， ${{t}_{\rm{a}}} \in {R^{M \times 1}}$ 表示离散的方位采样时间序列。

所有子区域的第i阶多项式系数组成的向量 ${{\varPsi }_i}$ 为

$\begin{split} {{\varPsi }_i} =\,& \left[ {{u}_{{\rm{sub}}\_1}}\left( {i + 1} \right)\;{{u}_{{\rm{sub}}\_2}}\left( {i + 1} \right)\;···\right.\\ & \left.{{u}_{{\rm{sub}}\_D}}\left( {i + 1} \right) \right]_{1 \times D}^{\rm{T}} \end{split}$

(18)

其中， ${{u}_{{\rm{sub}}\_k}}\left( {i + 1} \right)$ 表示向量 ${{u}_{{\rm{sub}}\_k}}$ 中的第i+1个元素。

根据式(16)可知，由子区域位置决定的第i阶空变系数矩阵 ${{\varOmega }_i}$ 分别表示为

$\left. \begin{split} & {{\varOmega }_2} = {\left[ \begin{array}{*{20}{c}} 1&{t_{{\rm{n}}\_1}}&t_{{\rm{n}}\_1}^2&\Delta {R_1}&\Delta R_1^2\\ 1&{t_{{\rm{n}}\_2}}&t_{{\rm{n}}\_2}^2&\Delta {R_2}&\Delta R_2^2\\ {\rm{}}&{\rm{}} & \vdots & {\rm{}}&{\rm{}} \\ 1&{t_{{\rm{n}}\_D}}&t_{{\rm{n}}\_D}^2&\Delta {R_D}&\Delta R_D^2 \end{array} \right]_{5 \times D}}\\ & {{\varOmega }_3} = {\left[\!\!\! \begin{array}{l} 1\;\;{t_{{\rm{n}}\_1}}\;\;\Delta {R_1}\\ 1\;\;{t_{{\rm{n}}\_2}}\;\;\Delta {R_2}\\ \quad \vdots \\ 1\;\;{t_{{\rm{n}}\_D}}\;\;\Delta {R_D} \end{array} \!\!\!\right]_{{\rm{3}} \times D}},{{\varOmega }_{\rm{4}}} = {\left[\!\!\! \begin{array}{l} 1\;\;\Delta {R_1}\\ 1\;\;\Delta {R_2}\\ \quad \vdots \\ 1\;\;\Delta {R_D} \end{array}\!\!\! \right]_{{\rm{2}} \times D}}\\ \end{split}\right\}$

(19)

其中， ${t_{{\rm{n}}\_k}}$ 和 $\Delta {R_k}$ 分别表示第i个子区域中心点的方位和距离位置。

基于最小二乘法，第i阶空变多项式系数向量 ${{\varLambda }_i}$ 可表示为

${{\varLambda }_i} = {\varOmega }_i^\dagger \cdot {{\varPsi }_i},\ \ i = 2,\;3,\;{\rm{4}}$

(20)

其中“ $\dagger$ ”表示广义逆运算， ${{\varLambda }_i}$ 的具体形式为

$\left. \begin{split} & {{\varLambda }_2} \!=\! \left[ {{b_0}\;{b_{{\rm{a1}}}}\;{b_{{\rm{a2}}}}\;{b_{{\rm{r1}}}}\;{b_{{\rm{r2}}}}} \right]_{1 \times 5}^{\rm{T}},{{\varLambda }_3} \!=\! \left[ {{c_0}\;{c_{{\rm{a1}}}}\;{c_{{\rm{r1}}}}\;} \right]_{1 \times 3}^{\rm{T}}\\ & {{\varLambda }_3} = \left[ {{d_0}\;{d_{{\rm{r1}}}}\;} \right]_{1 \times 2}^{\rm{T}} \end{split}\right\}\!\!\!\!\!$

(21)

获取误差相位的空变多项式系数 ${{\varLambda }_i}$ 后，根据式(22)对式(3)中的空变多普勒参数进行修正，即可实现2维空变运动误差的补偿

$\left. \begin{aligned} & {g_{{\rm{2}}0}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{{\rm{2}}0}}\left( {{R_{\rm{f}}}} \right) + {b_0} + {b_{{\rm{r1}}}}\Delta R + {b_{{\rm{r1}}}}\Delta {R^2}\\ & {g_{{\rm{21}}}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{{\rm{2}}1}}\left( {{R_{\rm{f}}}} \right) + {b_{{\rm{a1}}}}\\ & {g_{{\rm{22}}}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{{\rm{2}}1}}\left( {{R_{\rm{f}}}} \right) + {b_{{\rm{a2}}}}\\ & {g_{30}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{30}}\left( {{R_{\rm{f}}}} \right) + {c_0} + {c_{{\rm{r1}}}}\Delta R,\\ & {g_{{\rm{31}}}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{31}}\left( {{R_{\rm{f}}}} \right) + {c_{{\rm{a1}}}}\\ & {g_{{\rm{40}}}}\left( {{R_{\rm{f}}}} \right) = {{\tilde g}_{40}}\left( {{R_{\rm{f}}}} \right) + {d_0} + {d_{{\rm{r1}}}}\Delta R \end{aligned} \right\}$

(22)

其中， ${\tilde g_x}\left( {{R_{\rm{f}}}} \right)$ 表示根据惯导参数计算的含误差的多普勒参数。

最终，所提机动平台大斜视SAR稀疏自聚焦方法流程如图2所示。由于所提方法采用稀疏自聚焦方法对运动误差进行估计，因此该方法可用于全采样数据下的匹配滤波成像以及欠采样数据下的稀疏成像。

图 2 机动平台大斜视SAR稀疏自聚焦方法流程

下载: 全尺寸图片幻灯片

3.4 算法的场景适用性分析

本文所提稀疏自聚焦方法对成像场景的适用性分析如下：

场景类型的要求：所提方法需要在成像场景的不同区域内选择若干子区域，采用稀疏自聚焦方法进行局部非空变相位误差的估计，要求成像场景具有一定的对比度。PGA通常要求场景中具有强散射点，MEA等图像准则自聚焦方法要求场景具有一定的对比度，所提方法对场景类型的要求与MEA相似，低于PGA。

场景大小的要求：对于机动平台大斜视SAR成像，非线性轨迹和大斜视角的存在使成像参数具有较强的空变性，本文采用Keystone变换和频域相位滤波法进行成像参数空变性的校正，运动误差产生的空变相位误差的校正通过修正频域相位滤波法的时频域滤波系数实现。由于运动误差的幅度远小于平台机动所造成的轨迹偏移，因此成像场景的大小主要由频域相位滤波法的空变性校正能力决定，在频域相位滤波法的有效成像区域内，所提的空变运动误差补偿方法均是有效的。

3.5 运算量分析

本文基于Keystone变换和频域相位滤波法构造了如图1所示的机动平台大斜视SAR频域成像算法。在采用稀疏自聚焦方法估计全局非空变相位误差时，在所有的距离单元中仅需选取平均能量排序前5%～10%的距离单元即可取得理想的效果，这样可以极大地降低矩阵维度，提高算法效率。在对相位误差进行估计时，所提方法仅利用了距离压缩回波 ${{S}_{{\rm{rc}}}}$ 及相应的频域算子 ${{{\varGamma}} ^{ - 1}}\left( \cdot \right)$ 和 ${{\varGamma}} \left( \cdot \right)$ 。频域算子共包含3次方位向FFT/IFFT运算和两次矩阵点乘运算，设其运算量为 ${C_\varGamma }$ 。

设稀疏自聚焦的迭代次数为 ${I_{\max }}$ ，每次迭代需要计算2次频域算子 ${{{\varGamma}} ^{ - 1}}\left( \cdot \right)$ 或 ${{\varGamma}} \left( \cdot \right)$ 。在图2的空变运动误差估计过程中，设估计全局非空变运动误差时选用的距离单元占全部距离单元的比例为 ${\eta _1}$ ，估计子图像相位误差时，每个子图像的距离单元占全部距离单元的比例为 ${\eta _2}$ ，则空变运动误差估计所需的运算量为

${C_{{\rm{moco}}}} = 2\left( {{\eta _1} + D{\eta _2}} \right){I_{\max }}{C_\varGamma }$

(23)

仿真实验表明， ${I_{\max }} = 30$ , ${\eta _1} = 0.1$ , ${\eta _2} = 0.02$ , $D = 8$ 即可高精度地估计空变的运动误差，所需的运算量为15.6 ${C_\varGamma }$ 。在图2中，实现方位压缩的成像算子 $\varGamma \left( \cdot \right)$ 的运算量约占整个算法运算量的1/4，因此所提方法进行空变运动误差估计的运算量约为 $15.6/4 = 3.9$ 次频域匹配滤波成像的运算量，在SAR稀疏成像中仅相当于2次迭代的运算量，具有较高的运算效率。

4. 仿真分析

机动平台大斜视SAR的实测数据还难以获取，本节采用文献[17]的方法模拟真实SAR场景的回波数据验证所提方法的有效性。仿真采用的SAR系统和平台运动参数如表1所示，选择含有少量强散射点且稀疏性较低的场景1用于全采样数据成像实验，含有大量强散射点且稀疏性较高的场景2用于稀疏数据成像实验，场景1和场景2均平行于X轴放置，分别如图3(a)和图3(b)所示。根据常规机载SAR的惯导数据，加入如图3(c)所示的3维运动误差。

表 1 仿真参数

参数	数值	参数	数值
载频	17 GHz	地面斜视角	60°
距离带宽	300 MHz	平台高度	4 km
合成孔径时间	3 s	中心斜距	12 km
脉冲宽度	5 μs	速度	(150, 0, –30) m/s
脉冲重复频率	1 kHz	加速度	(2.2, 1.1, –1.8) m/s²

下载: 导出CSV

| 显示表格

图 3 仿真场景和3维运动误差曲线

下载: 全尺寸图片幻灯片

为验证本文所提2维空变相位误差估计与校正方法的有效性，图4给出了全采样数据下场景1的匹配滤波成像结果，同时选择加权PGA(Weighted PGA, WPGA)^[7]和基于近似观测的稀疏自聚焦方法^[12]作为对比算法，图4中矩形框所选择的子区域为本文方法估计空变相位误差时所选择的子区域。从图4中可以看出，由于WPGA方法对强散射点的依赖较强，对于强散射点较少且对比度较低的场景1, WPGA方法无法有效聚焦；稀疏自聚焦方法^[12]能够明显提高聚焦质量，但依旧存在一定的散焦情况，而本文方法具有最好的聚焦效果。

为直观体现本文方法的空变误差校正效果，图5放大显示了图4中部分子区域成像结果，子区域序号对应的子区域与图4中的标号一致。由于 WPGA方法的聚焦效果明显差于另两种方法，因此图5未展示WPGA方法聚焦后的子区域成像结果。从图5中可以看出，稀疏自聚焦方法可以估计全局的非空变误差相位，但残余的空变误差相位降低了局部子区域的聚焦质量，本文方法同时估计了距离和方位向的空变多普勒系数，能够校正子区域的空变相位误差，对场景1中不同的子区域均有较好的聚焦效果。为进一步量化分析所提方法的聚焦效果，采用图像熵和对比度量化分析图4中3种方法的聚焦效果，结果如表2所示。可以看出，本文方法聚焦图像的熵值最小，对比度最高，具有最好的聚焦效果。

图 4 全采样数据下的场景1成像结果对比

下载: 全尺寸图片幻灯片

图 5 场景1局部区域成像结果

下载: 全尺寸图片幻灯片

表 2 场景1成像结果量化分析结果

成像方法	熵	对比度
WPGA	14.58	3.95
稀疏自聚焦	14.42	6.82
本文方法	14.31	7.02

下载: 导出CSV

| 显示表格

为验证本文方法的稀疏成像效果，抽取场景2的36%原始回波数据进行成像处理，其中稀疏采样矩阵L中的降采样率 ${\xi _{\rm{a}}}$ 和 ${\xi _{\rm{r}}}$ 均为0.6，场景2的成像结果如图6所示，其中WPGA、稀疏自聚焦和本文方法聚焦图像的熵值分别为15.50,12.06和11.95。从图6中可以看出，距离和方位向的欠采样使基于WPGA的匹配滤波方法的成像结果存在严重的欠采样噪声，本文方法和稀疏自聚焦方法均可以有效去除这种欠采样噪声，同时由于本文方法校正了空变的相位误差，具有更小的熵值和更好的稀疏成像效果。

图 6 欠采样数据下的场景2成像结果对比

下载: 全尺寸图片幻灯片

5. 结束语

本文提出了一种适用于聚束式机动平台大斜视SAR的空变运动误差估计与补偿方法，该方法结合Keystone变换和频域相位滤波法构造了近似观测算子，并采用基于近似观测的稀疏自聚焦方法估计全局非空变和局部空变的误差相位。所提方法仅抽取少部分距离单元进行全局非空变相位误差的估计，具有较高的运算效率，能够用于全采样和欠采样数据下的自聚焦处理，仿真实验验证了所提方法的有效性。受限于频域相位滤波法的多普勒参数空变校正能力，本文方法仅适用于低阶的空变运动误差，下一步将研究高阶空变运动误差下的稀疏自聚焦方法。

图 1 改进AHP法框架示意图

下载: 全尺寸图片幻灯片

图 2 基于DQN的WTA决策模型

下载: 全尺寸图片幻灯片

图 3 固定场景下DQN训练效果

下载: 全尺寸图片幻灯片

图 4 固定场景下DQN火力分配方案

下载: 全尺寸图片幻灯片

图 5 固定场景下仅考虑全局收益的DQN训练效果

下载: 全尺寸图片幻灯片

图 6 1000次蒙特卡罗仿真训练

下载: 全尺寸图片幻灯片

表 1 目标属性值

编号	攻击地重要度	剩余飞行时间(s)	最大高度 (km)	关机点速度(km/s)	RCS (m²)
1	4	220	260	2.3	0.007
2	9	250	225	2.1	0.005
3	4	530	630	4.2	0.012
4	2	550	680	4.8	0.013
5	6	240	235	2.2	0.010
6	2	610	710	5.1	0.015
7	1	1200	1600	6.8	0.017
8	0	1120	1450	6.6	0.016
9	2	1400	75	7.4	0.006
10	3	1500	78	7.1	0.007

下载: 导出CSV

表 2 传统和改进AHP方法的评估指标权重计算结果对比

	攻击地重要度	剩余飞行时间(s)	最大高度 (km)	关机点速度(km/s)	RCS (m²)
传统AHP	0.34	0.27	0.08	0.12	0.19
改进AHP	0.44	0.17	0.16	0.13	0.10

下载: 导出CSV

表 3 改进AHP与传统AHP法的目标威胁度评估结果

	编号
	8	7	9	4	6
改进AHP法	0.125	0.119	0.111	0.107	0.106
传统AHP法	0.115	0.110	0.104	0.107	0.106
	编号
	10	3	1	5	2
改进AHP法	0.104	0.095	0.091	0.078	0.060
传统AHP法	0.099	0.097	0.097	0.088	0.075

下载: 导出CSV

表 4 测试用例参数

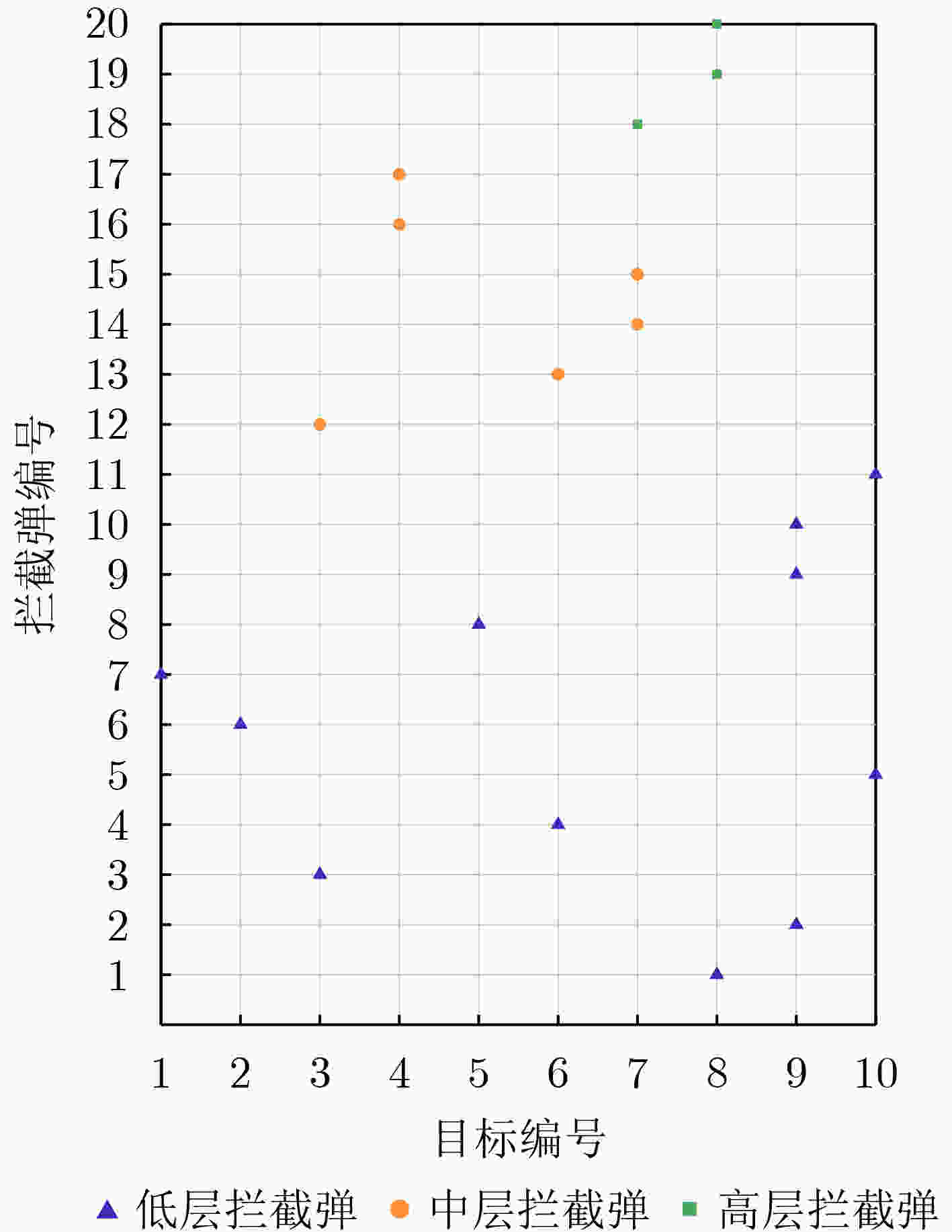
测试用例编号	目标数量比	拦截弹数量比
#1	5:5:3:2	12:8:5
#2	10:8:5:2	18:15:12
#3	12:9:9:5	25:15:10

下载: 导出CSV

表 5 3种场景测试结果

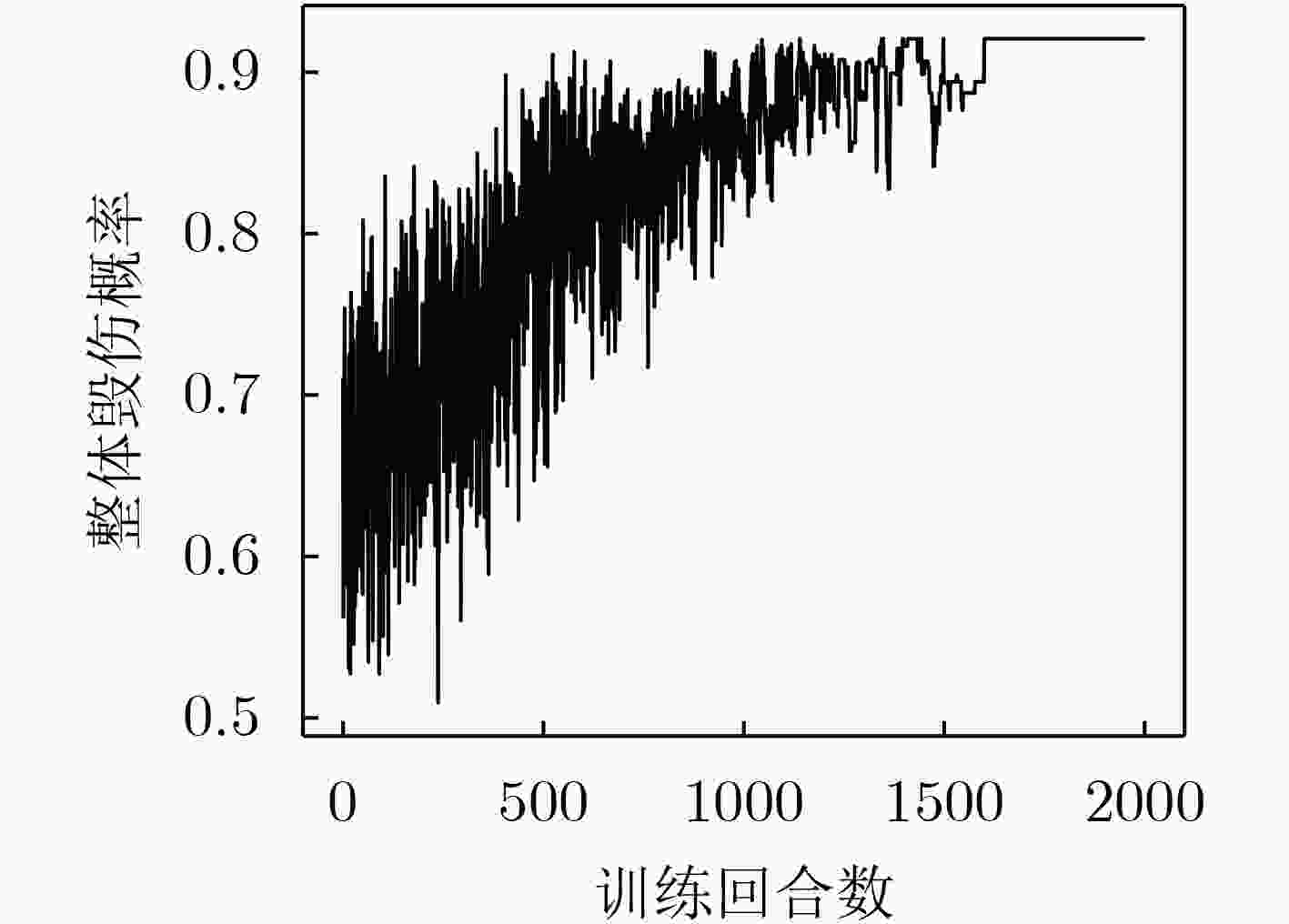
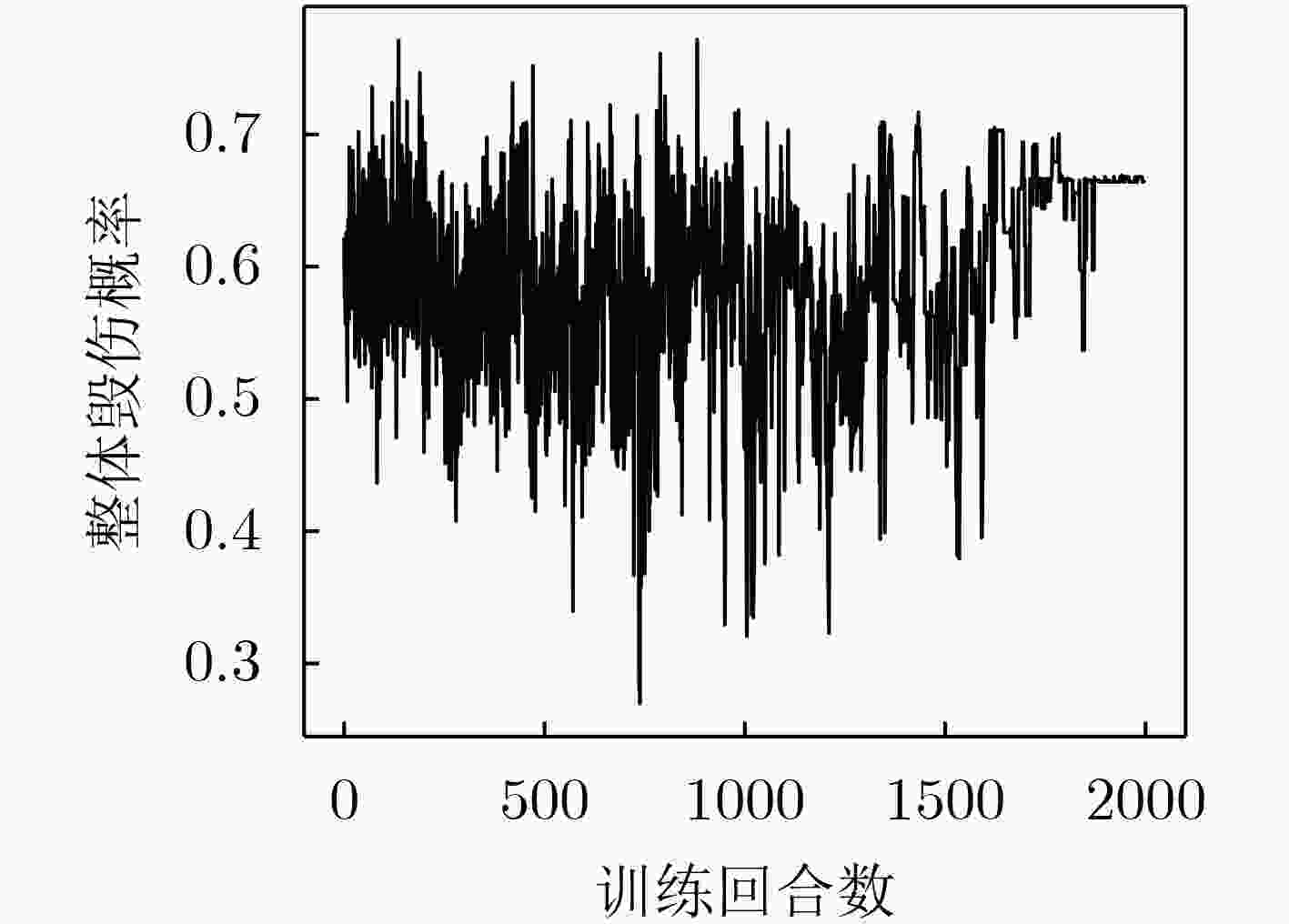
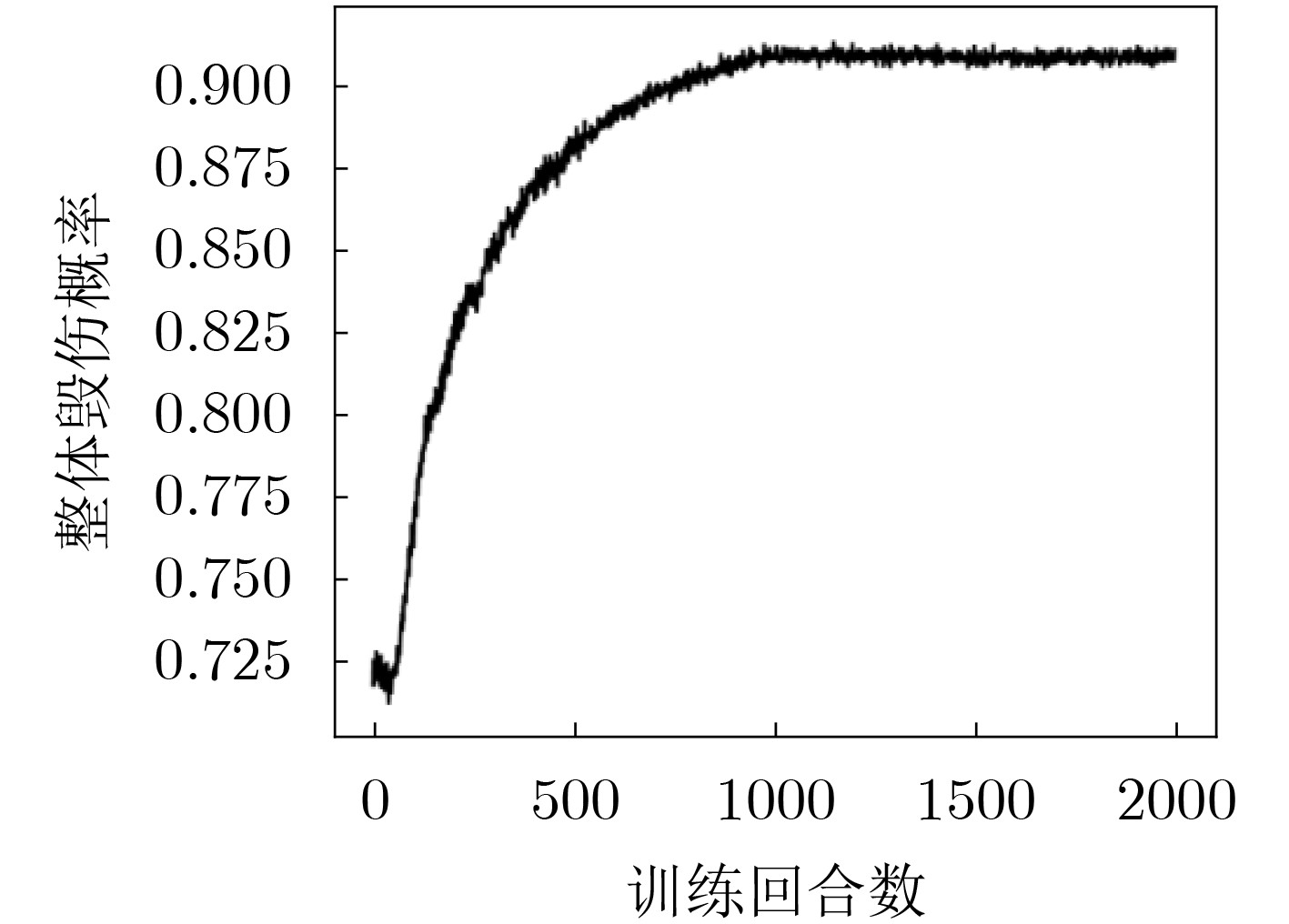
指标	测试用例编号	分配方案求解方法
指标	测试用例编号	DQN	PSO	随机法
整体毁伤概率	#1	0.921	0.982	0.620
	#2	0.918	0.907	0.590
	#3	0.856	0.758	0.540
运行时间(s)	#1	0.050	22.001	0.001
	#2	0.170	62.021	0.003
	#3	0.220	137.000	0.019

下载: 导出CSV

参考文献(16)

[1]	KLINE A, AHNER D, and HILL R. The weapon-target assignment problem[J]. Computers & Operations Research, 2019, 105: 226–236. doi: 10.1016/j.cor.2018.10.015
[2]	YUE Jiao and ZHANG Ke. Vulnerability Threat assessment based on AHP and fuzzy comprehensive evaluation[C]. 2014 IEEE Seventh International Symposium on Computational Intelligence and Design, Hangzhou, China, 2014: 513–516.
[3]	杨罗章, 胡生亮, 冯士民. 基于Entropy-TOPSIS方法的目标威胁动态评估与仿真[J]. 兵工自动化, 2020, 39(3): 53–56,60. doi: 10.7690/bgzdh.2020.03.012 YANG Luozhang, HU Shengliang, and FENG Shimin. Dynamic evaluation and simulation of targets threat based on entropy and TOPSIS method[J]. Ordnance Industry Automation, 2020, 39(3): 53–56,60. doi: 10.7690/bgzdh.2020.03.012
[4]	陈龙, 马亚平. 基于分层贝叶斯网络的航母编队对潜威胁评估[J]. 系统仿真学报, 2017, 29(9): 2206–2212,2220. doi: 10.16182/j.issn1004731x.joss.201709044 CHEN Long and MA Yaping. Threat assessment of aircraft carrier formation based on hierarchical Bayesian network[J]. Journal of System Simulation, 2017, 29(9): 2206–2212,2220. doi: 10.16182/j.issn1004731x.joss.201709044
[5]	杨爱武, 李战武, 徐安, 等. 基于RS-CRITIC的空战目标威胁评估[J]. 北京航空航天大学学报, 2020, 46(12): 2357–2365. doi: 10.13700/j.bh.1001-5965.2019.0638 YANG Aiwu, LI Zhanwu, XU An, et al. Threat assessment of air combat target based on RS-CRITIC[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(12): 2357–2365. doi: 10.13700/j.bh.1001-5965.2019.0638
[6]	LLOYD S P and WITSENHAUSE H S. Weapon allocation is NP-Complete[C]. The IEEE Summer Simulation Conference, Reno, USA, 1986: 1054–1058.
[7]	王邑, 孙金标, 肖明清, 等. 基于类型2区间模糊K近邻分类器的动态武器目标分配方法研究[J]. 系统工程与电子技术, 2016, 38(6): 1314–1319. doi: 10.3969/j.issn.1001-506X.2016.06.15 WANG Yi, SUN Jinbiao, XIAO Mingqing, et al. Research of dynamic weapon-target assignment problem based on type-2 interval fuzzy K-nearest neighbors classifier[J]. Systems Engineering and Electronics, 2016, 38(6): 1314–1319. doi: 10.3969/j.issn.1001-506X.2016.06.15
[8]	王净, 战凯, 晏峰. 基于动态规划算法的舰空导弹火力分配模型研究[J]. 舰船电子工程, 2011, 31(2): 24–26. doi: 10.3969/j.issn.1627-9730.2011.02.007 WANG Jing, ZHAN Kai, and YAN Feng. Ship-to-air missile firepower-distributing model study based on dynamic programming algorithm[J]. Ship Electronic Engineering, 2011, 31(2): 24–26. doi: 10.3969/j.issn.1627-9730.2011.02.007
[9]	丁立超, 黄枫, 潘伟. 基于改进混沌遗传算法的炮兵火力分配方法[J]. 系统仿真技术, 2021, 17(1): 12–16. doi: 10.16812/j.cnki.cn31-1945.2021.01.003 DING Lichao, HUANG Feng, and PAN Wei. Artillery fire allocation method based on improved chaotic genetic algorithm[J]. System Simulation Technology, 2021, 17(1): 12–16. doi: 10.16812/j.cnki.cn31-1945.2021.01.003
[10]	李俨, 董玉娜. 基于SA-DPSO混合优化算法的协同空战火力分配[J]. 航空学报, 2010, 31(3): 626–631. LI Yan and DONG Yu’na. Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 626–631.
[11]	SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354–359. doi: 10.1038/nature24270
[12]	ZHU Yuke, MOTTAGHI R, KOLVE E, et al. Target-driven visual navigation in indoor scenes using deep reinforcement learning[C]. 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 2017: 3357–3364.
[13]	施伟, 冯旸赫, 程光权, 等. 基于深度强化学习的多机协同空战方法研究[J]. 自动化学报, 2021, 47(7): 1610–1623. doi: 10.16383/j.aas.c201059 SHI Wei, FENG Yanghe, CHENG Guangquan, et al. Research on multi-aircraft cooperative air combat method based on deep reinforcement learning[J]. Acta Automatica Sinica, 2021, 47(7): 1610–1623. doi: 10.16383/j.aas.c201059
[14]	阎栋, 苏航, 朱军. 基于DQN的反舰导弹火力分配方法研究[J]. 导航定位与授时, 2019, 6(5): 18–24. doi: 10.19306/j.cnki.2095-8110.2019.05.003 YAN Dong, SU Hang, and ZHU Jun. Research on fire distribution method of anti-ship missile based on DQN[J]. Navigation Positioning and Timing, 2019, 6(5): 18–24. doi: 10.19306/j.cnki.2095-8110.2019.05.003
[15]	ZHU Yuxin, TIAN Dazuo, and YAN Feng. Effectiveness of entropy weight method in decision-making[J]. Mathematical Problems in Engineering, 2020, 2020: 3564835. doi: 10.1155/2020/3564835
[16]	MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236

施引文献

期刊类型引用(3)

1.	贺靖，谭鸽伟. 基于ALPFT参数估计的运动目标高分辨率成像. 航空学报. 2025(01): 260-274 . 百度学术
2.	稂时楠，许奔，崔祥斌. 基于快速后向投影的超宽带冰雷达数据成像算法. 电子与信息学报. 2022(04): 1249-1256 . 本站查看
3.	陈溅来，熊毅，徐刚，张俊超，杨德贵，梁步阁. 基于子图像变标的非线性轨迹SAR成像及其自聚焦方法. 雷达学报. 2022(06): 1098-1109 . 百度学术

其他类型引用(1)

资源附件(0)

访问统计

图(6) / 表(5)

计量

文章访问数: 1444
HTML全文浏览量: 737
PDF下载量: 161
被引次数: 4

1. 引言
2. 近似观测模型
3. 2维空变相位误差的估计与补偿
3.1 基于近似观测的稀疏自聚焦方法
3.2 空变的运动误差模型
3.3 空变误差相位的求解与补偿
3.4 算法的场景适用性分析
3.5 运算量分析
4. 仿真分析
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

融合多属性决策和深度Q值网络的反导火力分配方法

doi: 10.11999/JEIT211136

通讯作者:
方峰　fangf@hdu.edu.cn

计量

Weapon-Target Assignment Optimization Based on Multi-attribute Decision-making and Deep Q-Network for Missile Defense System

1. 引言

2. 近似观测模型

3. 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

3.2 空变的运动误差模型

3.3 空变误差相位的求解与补偿

3.4 算法的场景适用性分析

3.5 运算量分析

4. 仿真分析

5. 结束语

期刊类型引用(3)

其他类型引用(1)

计量

目录

1. 引言

2. 近似观测模型

3. 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

3.2 空变的运动误差模型

3.3 空变误差相位的求解与补偿

3.4 算法的场景适用性分析

3.5 运算量分析

4. 仿真分析

5. 结束语

留言板

融合多属性决策和深度Q值网络的反导火力分配方法

doi: 10.11999/JEIT211136

通讯作者: 方峰 fangf@hdu.edu.cn

计量

出版历程

Weapon-Target Assignment Optimization Based on Multi-attribute Decision-making and Deep Q-Network for Missile Defense System

1. 引言

2. 近似观测模型

3. 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

3.2 空变的运动误差模型

3.3 空变误差相位的求解与补偿

3.4 算法的场景适用性分析

3.5 运算量分析

4. 仿真分析

5. 结束语

期刊类型引用(3)

其他类型引用(1)

计量

出版历程

目录

1. 引言

2. 近似观测模型

3. 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

3.2 空变的运动误差模型

3.3 空变误差相位的求解与补偿

3.4 算法的场景适用性分析

3.5 运算量分析

4. 仿真分析

5. 结束语

通讯作者:
方峰　fangf@hdu.edu.cn