A Deep Learning Assisted Ground Penetrating Radar Localization Method
-
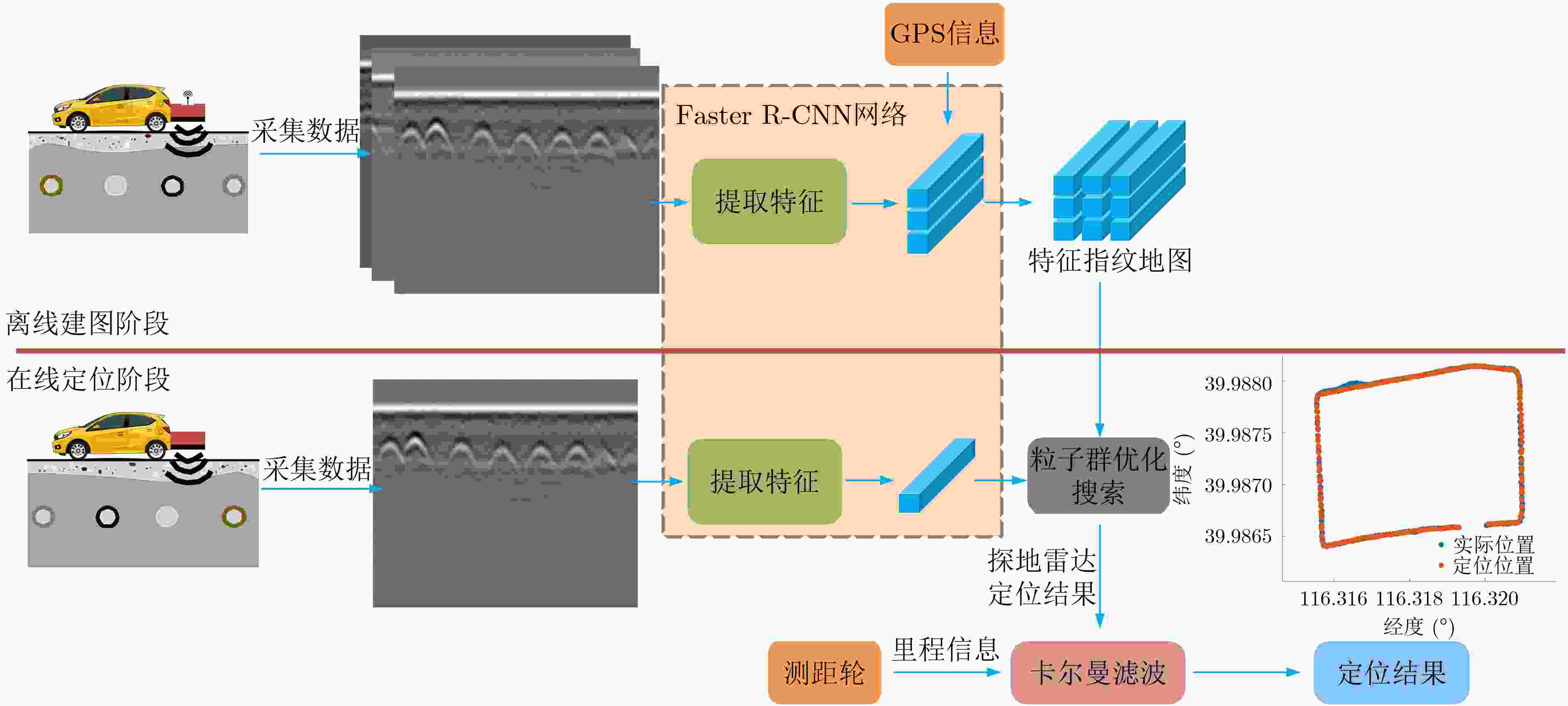
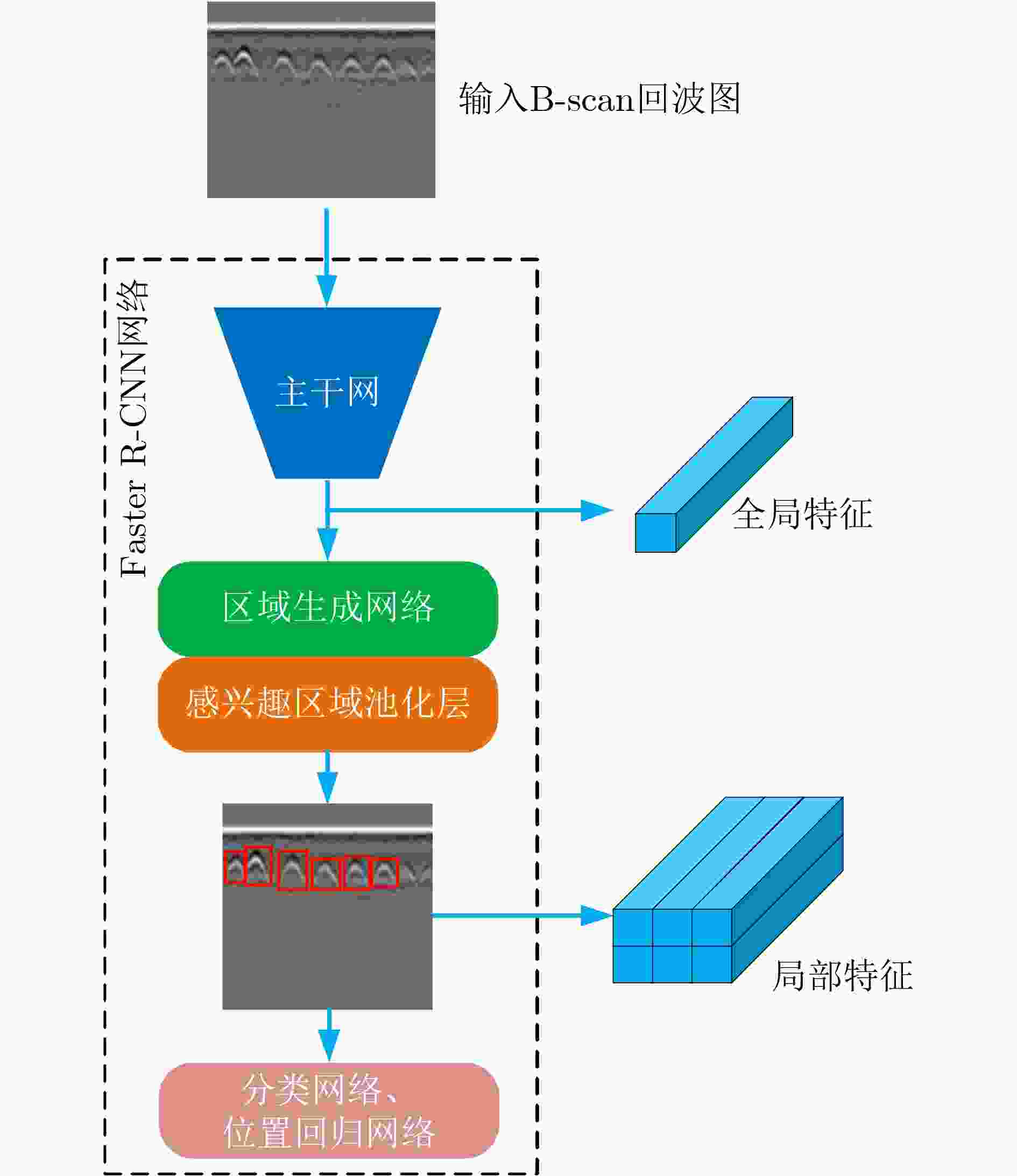
摘要: 在恶劣条件下,例如在雨、雪、沙尘、强光以及黑夜等环境下,自动驾驶方案中常用的视觉和激光传感器因为无法准确感知外界环境而面临失效问题。因此,该文提出一种通过深度学习辅助的探地雷达感知地下目标特征用于车辆定位的方法。所提方法分为离线建图和在线定位两个阶段。在离线建图阶段,首先利用探地雷达采集地下目标的回波数据,然后使用深度卷积神经网络(DCNN)提取采集的地下回波数据中的目标特征,同时存储提取的目标特征和当前地理位置信息,形成地下目标特征指纹地图。在定位阶段,首先利用DCNN提取探地雷达采集到的当前地下回波数据中的目标特征。然后基于粒子群优化方法搜索特征指纹地图中与当前提取的目标特征最相似的特征,并输出该特征的地理位置信息,作为探地雷达定位车辆的结果。最后利用卡尔曼滤波融合探地雷达定位结果和测距轮测量的里程信息,得到高精度的定位结果。实验选取地下目标丰富的场景和实际城市道路场景来测试所提方法的定位性能。实验结果表明,与单一使用探地雷达原始回波数据地图的定位方法相比,深度学习辅助的探地雷达定位方法能避免直接计算原始雷达回波数据间的相似度,减少数据计算量以及数据传输量,具有实时定位能力,同时特征指纹地图对回波数据的变化有鲁棒性,因此所提方法的平均定位误差减少约70%。深度学习辅助的探地雷达定位方法可作为未来自动驾驶车辆在恶劣环境下感知定位方法的补充。Abstract: Under harsh conditions, such as rain, snow, dust, strong light, and dark night, the vision and laser sensors commonly used in autonomous driving solutions may fail because they can not accurately sense the external environment. Therefore, a method for vehicle localization using underground target features sensed by deep learning assisted ground penetrating radar is proposed in this paper. The proposed method is divided into two phases: offline mapping phase and online localization phase. In the offline mapping phase, the ground penetrating radar is used to collect the echo data from the underground targets first, then the Deep Convolutional Neural Network (DCNN) is utilized to extract the target features from the collected echo data, and the extracted target features are saved with the current geographic location information to form a fingerprint map of underground target features. In the localization phase, the DCNN is used to extract the target features from the current echo data collected by the ground penetrating radar first, and then the target feature most similar to the current extracted target feature in the fingerprint map of underground target features is retrieved based on the particle swarm optimization method, and the geographic location information of the retrieved feature is marked as the vehicle localization result by the ground penetrating radar. Finally, the Kalman filter is used to fuse the ground penetrating radar localization result and the mileage information measured by the ranging wheel to obtain a high-precision localization result. The localization performance of the proposed localization method is tested on the experimental scenario with rich underground targets and the actual urban road scenario. The experimental results show that, compared with the single raw data-based ground penetrating radar localization method, the deep learning assisted ground penetrating radar localization method can avoid directly calculating the similarity between the raw radar data, reduce the amount of data computation and data transmission, and has the real-time localization capability. At the same time, the fingerprint map of underground target features is robust to the changes of the raw radar data, so the average localization error of the proposed method is reduced by about 70%. The deep learning assisted ground penetrating radar localization method can be used as a supplement to the detection and localization method of autonomous vehicles in harsh environments in the future.
-
表 1 系统详细参数
参数 参数值 探地雷达工作体制 脉冲体制 探地雷达中心频率 500 MHz 探地雷达等效采样速率 16 GHz 探地雷达采样点数 416点 探地雷达尺寸 0.46 m×0.35 m×0.20 m 重叠采样窗口大小M×n 416×416 重叠采样窗口间隔$\Delta n $ 5 道间距$ \Delta L $ 约0.01 m 车载平台行驶速度 约10 km/h 表 2 场景1中单次实验下不同方法的最大定位误差和计算时间比较
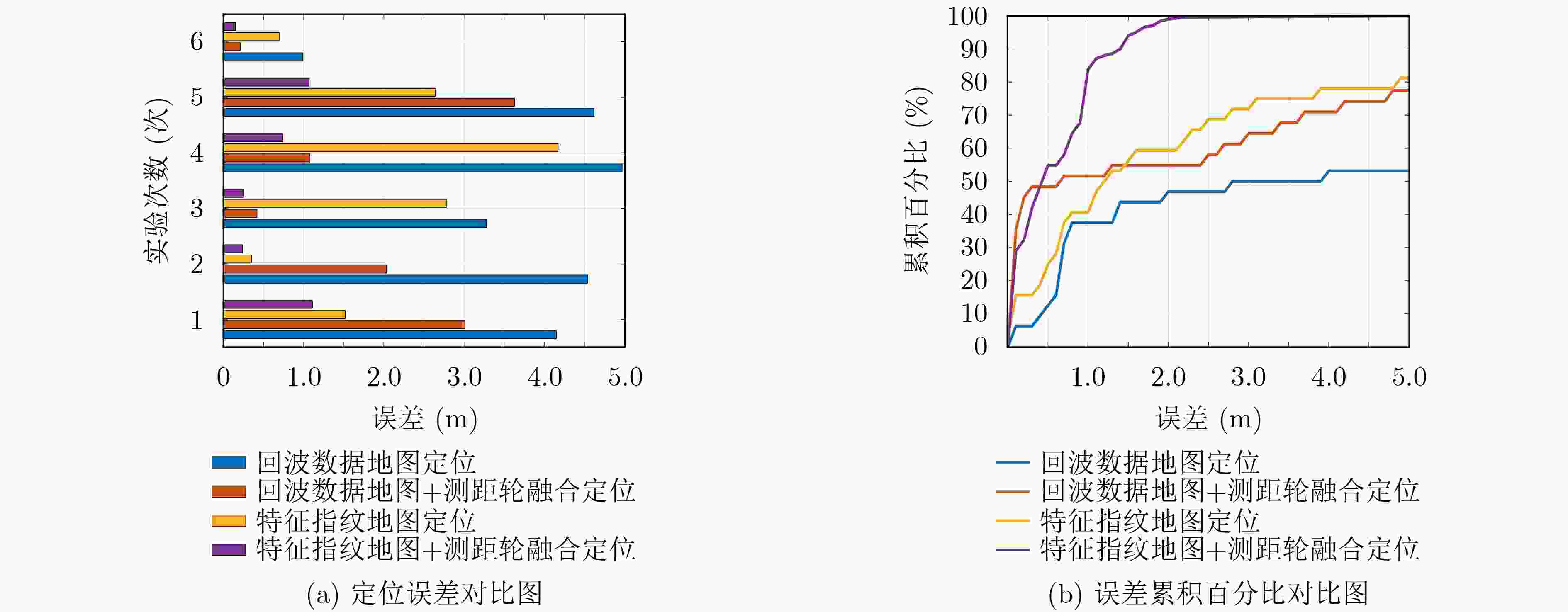
定位方法 最大误差(m) 定位频率(Hz) 回波数据地图定位 16.22 1.88 回波数据地图+测距轮融合定位 13.94 1.72 特征指纹地图定位 7.58 16.26 特征指纹地图+测距轮融合定位 1.49 15.18 表 3 场景2 中单次实验下不同方法的最大定位误差和计算时间比较
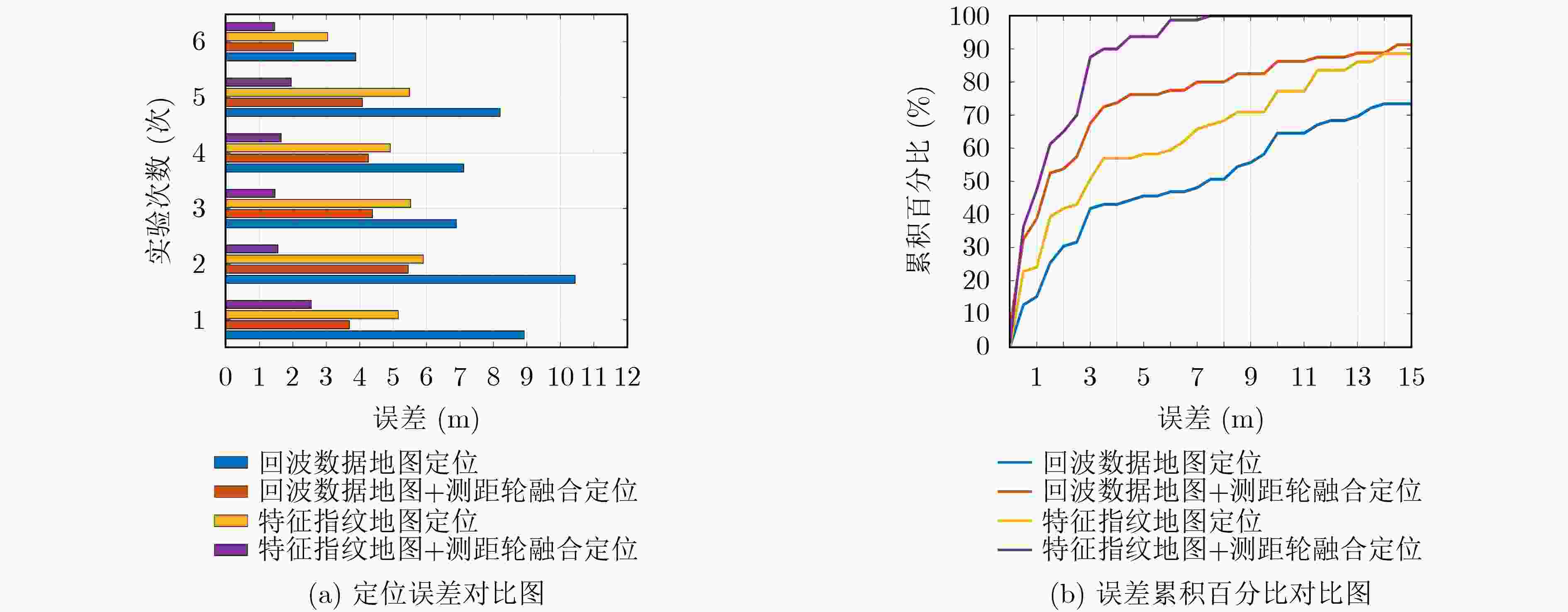
定位方法 最大误差(m) 定位频率(Hz) 回波数据地图定位 29.30 1.53 回波数据地图+测距轮融合定位 11.14 1.38 特征指纹地图定位 16.72 14.28 特征指纹地图+测距轮融合定位 2.82 13.11 -
[1] CAMPBELL S, O'MAHONY N, KRPALCOVA L, et al. Sensor technology in autonomous vehicles: A review[C]. 2018 29th Irish Signals and Systems Conference (ISSC), Belfast, UK, 2018: 1–4. [2] 史增凯, 马祥泰, 钱昭勇, 等. 基于北斗卫星导航系统非组合精密单点定位算法的精密授时精度研究[J/OL]. 电子与信息学报, 待发表. doi: 10.1199/JEIT210629.SHI Zengkai, MA Xiangtai, QIAN Zhaoyong, et al. Accuracy of precise timing based on uncombined precise point positioning algorithm in BeiDou navigation satellite system[J/OL]. Journal of Electronics & Information Technology, To be published. doi: 10.1199/JEIT210629. [3] 刘国忠, 胡钊政. 基于SURF和ORB全局特征的快速闭环检测[J]. 机器人, 2017, 39(1): 36–45. doi: 10.13973/j.cnki.robot.2017.0036LIU Guozhong and HU Zhaozheng. Fast loop closure detection based on holistic features from SURF and ORB[J]. Robot, 2017, 39(1): 36–45. doi: 10.13973/j.cnki.robot.2017.0036 [4] WANG Yunting, PENG Chaochung, RAVANKAR A A, et al. A single LiDAR-based feature fusion indoor localization algorithm[J]. Sensors, 2018, 18(4): 1294. doi: 10.3390/s18041294 [5] CIAMPOLI L B, TOSTI F, ECONOMOU N, et al. Signal processing of GPR data for road surveys[J]. Geosciences, 2019, 9(2): 96. doi: 10.3390/geosciences9020096 [6] NI Zhikang, ZHAO Di, YE Shengbo, et al. City road cavity detection using YOLOv3 for ground-penetrating radar[C]. 18th International Conference on Ground Penetrating Radar, Golden, USA, 2020: 384–387. [7] LIU Hai, LIN Chunxu, CUI Jie, et al. Detection and localization of rebar in concrete by deep learning using ground penetrating radar[J]. Automation in Construction, 2020, 118: 103279. doi: 10.1016/j.autcon.2020.103279 [8] DONG Zehua, FANG Guangyou, ZHOU Bin, et al. Properties of lunar regolith on the Moon's Farside unveiled by Chang'E-4 lunar penetrating radar[J]. Journal of Geophysical Research:Planets, 2021, 126(6): e2020JE006564. doi: 10.1029/2020JE006564 [9] SKARTADOS E, KARGAKOS A, TSIOGAS E, et al. GPR Antenna localization based on A-Scans[C]. 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2019: 1–5. [10] CORNICK M, KOECHLING J, STANLEY B, et al. Localizing ground penetrating RADAR: A step toward robust autonomous ground vehicle localization[J]. Journal of Field Robotics, 2016, 33(1): 82–102. doi: 10.1002/rob.21605 [11] ORT T, GILITSCHENSKI I, and RUS D. Autonomous navigation in inclement weather based on a localizing ground penetrating radar[J]. IEEE Robotics and Automation Letters, 2020, 5(2): 3267–3274. doi: 10.1109/LRA.2020.2976310 [12] REN Shaoqing, HE Kaiming, GIRSHICK R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137–1149. doi: 10.1109/TPAMI.2016.2577031 [13] PHAM M T and LEFÈVRE S. Buried object detection from B-scan ground penetrating radar data using Faster-RCNN[C]. IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018: 6804–6807. [14] SALVADOR A, GIRÓ-I-NIETO X, MARQUÉS F, et al. Faster R-CNN features for instance search[C]. The 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, USA, 2016: 394–401. [15] XU Song, CHOU W, and DONG Hongyi. A robust indoor localization system integrating visual localization aided by CNN-based image retrieval with Monte Carlo localization[J]. Sensors, 2019, 19(2): 249. doi: 10.3390/s19020249 [16] CHAI T and DRAXLER R R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247–1250. doi: 10.5194/gmd-7-1247-2014 [17] 陈勇, 郑瀚, 沈奇翔, 等. 基于改进免疫粒子群优化算法的室内可见光通信三维定位方法[J]. 电子与信息学报, 2021, 43(1): 101–107. doi: 10.11999/JEIT190936CHEN Yong, ZHENG Han, SHEN Qixiang, et al. Indoor three-dimensional positioning system based on visible light communication using improved immune PSO algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(1): 101–107. doi: 10.11999/JEIT190936 [18] 胡钊政, 刘佳蕙, 黄刚, 等. 融合WiFi、激光雷达与地图的机器人室内定位[J]. 电子与信息学报, 2021, 43(8): 2308–2316. doi: 10.11999/JEIT200671HU Zhaozheng, LIU Jiahui, HUANG Gang, et al. Integration of WiFi, laser, and map for robot indoor localization[J]. Journal of Electronics &Information Technology, 2021, 43(8): 2308–2316. doi: 10.11999/JEIT200671 -





 下载:
下载:


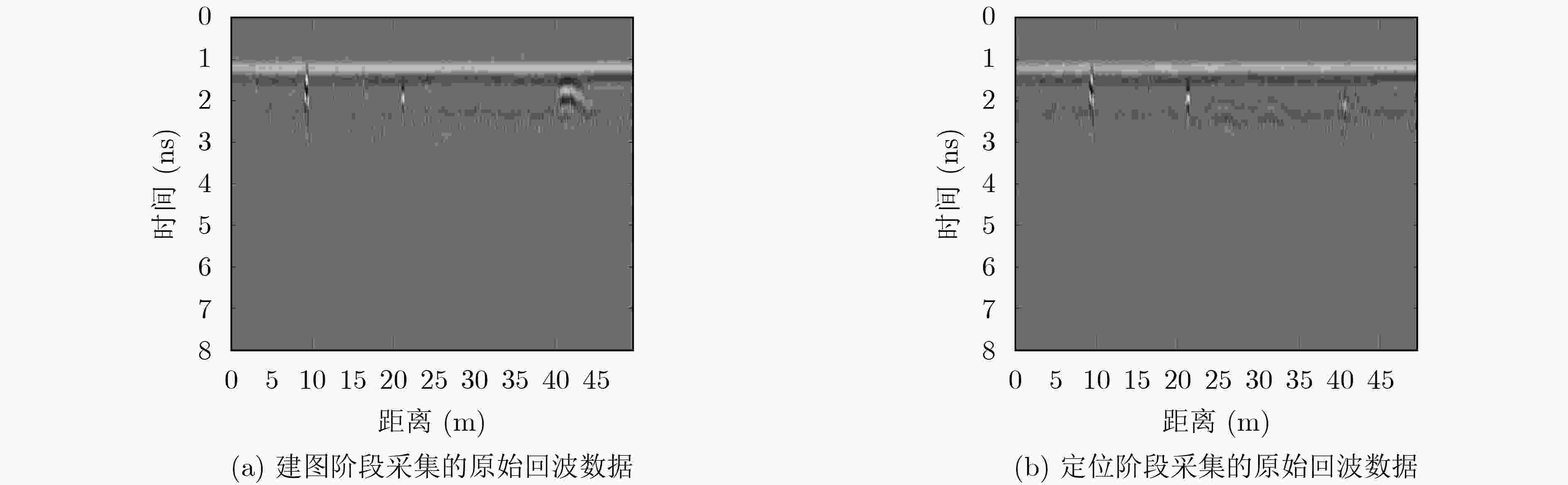
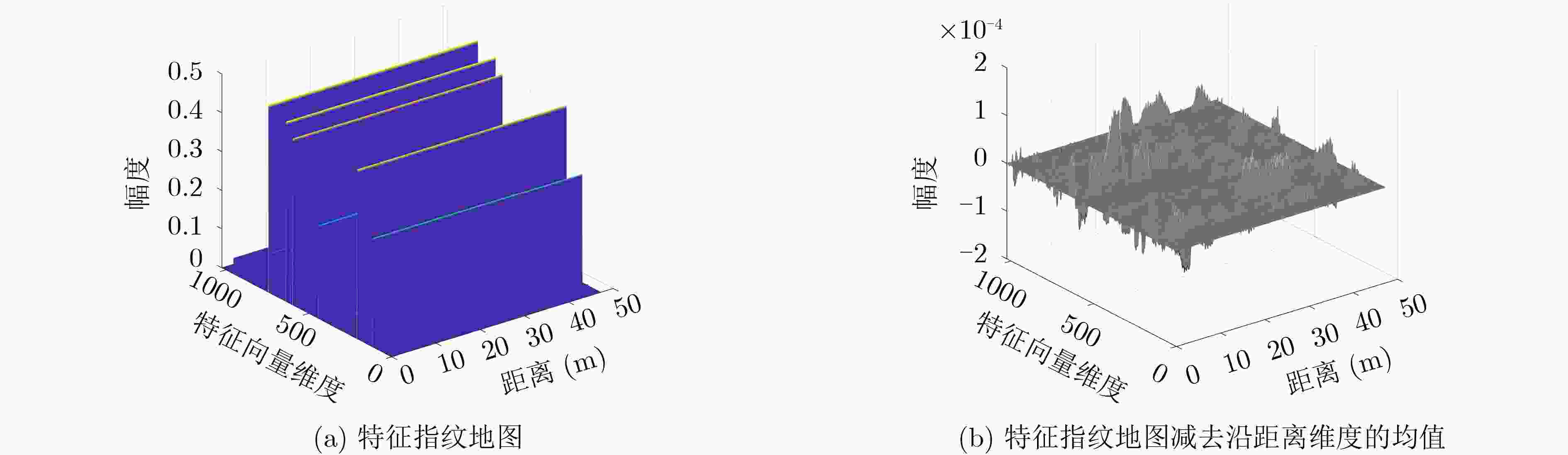


 下载:
下载:
