A Target Location Algorithm for Through-wall Radar Based on Improved Viterbi Frequency Estimation Technology
-
摘要: 针对多普勒穿墙雷达目标定位中难以从频率混叠区域准确提取定位信号的问题,该文提出一种基于改进Viterbi频率估计技术的目标定位算法。根据雷达回波的局部特性动态调整指数平滑法的平滑系数,并基于动态指数平滑预测数据定义Viterbi算法的新型惩罚函数。利用估计的目标频率曲线解调回波信号,完成对多个目标分量的分离,并结合多普勒处理方法合成目标运动轨迹,实现对目标的实时定位。实验结果表明,该方法有效抑制了算法在频率模糊区域的路径分叉问题,在多人体目标跟踪定位的应用场景中具有优越性。此外,新算法所采用的最佳路径搜索方式对传统Viterbi算法的全平面搜索进行了改进,有效提高了最佳路径的寻找效率。Abstract: Considering the problem of target signal identification in frequency ambiguity region of Doppler through wall radar, and the path bifurcation problem of traditional Viterbi algorithm in instantaneous frequency estimation, a target location algorithm based on improved Viterbi frequency estimation technology is proposed. According to the local characteristics of radar echo, the smoothing coefficient of exponential smoothing method is dynamically adjusted, and a new penalty function based on dynamic exponential smoothing prediction is defined. The echo signal is demodulated by the estimated target frequency curve to separate multiple target components, and the target motion trajectory is synthesized by combining Doppler processing to realize real-time target positioning. The experimental results show that the path bifurcation problem in frequency ambiguity region is effectively suppressed by this method, and this method has advantages in the application scene of multi-body target tracking and location. In addition, the employed dynamic search method enhances upon traditional whole-plane search and improves the efficiency of searching the optimal paths considerably.
-
Key words:
- Through-wall radar /
- Target location /
- Viterbi algorithm /
- Hough transform
-
表 1 目标频率无交叠场景的3种定位算法对应均方根误差及处理时间
均方根误差及处理时间 STFT 传统Viterbi算法 基于指数平滑预测的改进Viterbi算法 目标1频率(Hz) 0.0119 0.0091 0.0073 目标1定位(m) 0.43 0.18 0.08 目标2频率(Hz) 0.0092 0.0084 0.0061 目标2定位(m) 0.58 0.50 0.19 处理时间(s) 13 29 19 表 2 目标频率交叠场景的3种定位算法对应均方根误差及处理时间
均方根误差及处理时间 STFT 传统Viterbi算法 基于指数平滑预测的改进Viterbi算法 目标1频率(Hz) 0.23 2.82 0.10 目标1定位(m) 0.33 1.69 0.09 目标2频率(Hz) 0.35 4.07 0.14 目标2定位(m) 2.18 1.37 0.18 处理时间(s) 13 29 19 -
[1] ZHU Fang, WANG Kuangda, and WU Ke. A fundamental-and-harmonic dual-frequency Doppler radar system for vital signs detection enabling radar movement self-cancellation[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(11): 5106–5118. doi: 10.1109/TMTT.2018.2869591 [2] ZHAO Ganlin, LIANG Qilian, and DURRANI T S. UWB radar target detection based on hidden Markov models[J]. IEEE Access, 2018, 6: 28702–28711. doi: 10.1109/ACCESS.2018.2839690 [3] 杨宏宇, 王峰岩. 基于深度卷积神经网络的气象雷达噪声图像语义分割方法[J]. 电子与信息学报, 2019, 41(10): 2373–2381. doi: 10.11999/JEIT190098YANG Hongyu and WANG Fengyan. Meteorological radar noise image semantic segmentation method based on deep convolutional neural network[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2373–2381. doi: 10.11999/JEIT190098 [4] DING Yipeng, SUN Yinhua, YU Xiali, et al. Bezier-based Hough transforms for Doppler localization of human targets[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(1): 173–177. doi: 10.1109/LAWP.2019.2956842 [5] ABDOUSH Y, POJANI G, and CORAZZA G E. Adaptive instantaneous frequency estimation of multicomponent signals based on linear time–frequency transforms[J]. IEEE Transactions on Signal Processing, 2019, 67(12): 3100–3112. doi: 10.1109/TSP.2019.2912132 [6] 蒋留兵, 周小龙, 车俐. 基于无载波超宽带雷达的小样本人体动作识别[J]. 电子学报, 2020, 48(3): 602–615. doi: 10.3969/j.issn.0372-2112.2020.03.025JIANG Liubing, ZHOU Xiaolong, and CHE Li. Few-shot learning for human motion recognition based on carrier-free UWB radar[J]. Acta Electronica Sinica, 2020, 48(3): 602–615. doi: 10.3969/j.issn.0372-2112.2020.03.025 [7] ZÃO L and COELHO R. On the estimation of fundamental frequency from nonstationary noisy speech signals based on the Hilbert–Huang transform[J]. IEEE Signal Processing Letters, 2018, 25(2): 248–252. doi: 10.1109/LSP.2017.2782267 [8] 张林, 李秀友, 刘宁波, 等. 基于分形特性改进的EMD目标检测算法[J]. 电子与信息学报, 2016, 38(5): 1041–1046. doi: 10.11999/JEIT150731ZHANG Lin, LI Xiuyou, LIU Ningbo, et al. Improved EMD target detection method based on mono fractal characteristics[J]. Journal of Electronics &Information Technology, 2016, 38(5): 1041–1046. doi: 10.11999/JEIT150731 [9] WU Wei, WANG Guohong, and SUN Jinping. Polynomial Radon-Polynomial Fourier transform for near space hypersonic maneuvering target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1306–1322. doi: 10.1109/TAES.2017.2780658 [10] DJUROVIĆ I and STANKOVIĆ L. An algorithm for the Wigner distribution based instantaneous frequency estimation in a high noise environment[J]. Signal Processing, 2004, 84(3): 631–643. doi: 10.1016/j.sigpro.2003.12.006 [11] LI Po and ZHANG Qinghai. An improved Viterbi algorithm for IF extraction of multicomponent signals[J]. Signal, Image and Video Processing, 2018, 12(1): 171–179. doi: 10.1007/s11760-017-1143-2 [12] 苏小凡, 肖瑞, 朱明哲. 一种多分量调频信号瞬时频率估计方法[J]. 西安电子科技大学学报, 2019, 46(1): 51–56. doi: 10.19665/j.issn1001-2400.2019.01.009SU Xiaofan, XIAO Rui, and ZHU Mingzhe. Method for IF estimation of multicomponent FM signals[J]. Journal of Xidian University, 2019, 46(1): 51–56. doi: 10.19665/j.issn1001-2400.2019.01.009 [13] RITCHIE M, ASH M, CHEN Qingchao, et al. Through wall radar classification of human micro-Doppler using singular value decomposition analysis[J]. Sensors, 2016, 16(9): 1401. doi: 10.3390/s16091401 [14] LIN A and LING Hao. Doppler and direction-of-arrival (DDOA) radar for multiple-mover sensing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1496–1509. doi: 10.1109/TAES.2007.4441754 [15] AHMAD F, AMIN M G, and ZEMANY P D. Performance analysis of dual-frequency CW radars for motion detection and ranging in urban sensing applications[C]. SPIE 6547 Radar Sensor Technology XI, Orlando, USA, 2007: 65470K. [16] LU Huitian, KOLARIK W J, and LU S S. Real-time performance reliability prediction[J]. IEEE Transactions on Reliability, 2001, 50(4): 353–357. doi: 10.1109/24.983393 [17] DING Yipeng, LEI Chengxi, XU Xuemei, et al. Human micro-Doppler frequency estimation approach for Doppler radar[J]. IEEE Access, 2018, 6: 6149–6159. doi: 10.1109/ACCESS.2018.2793277 -





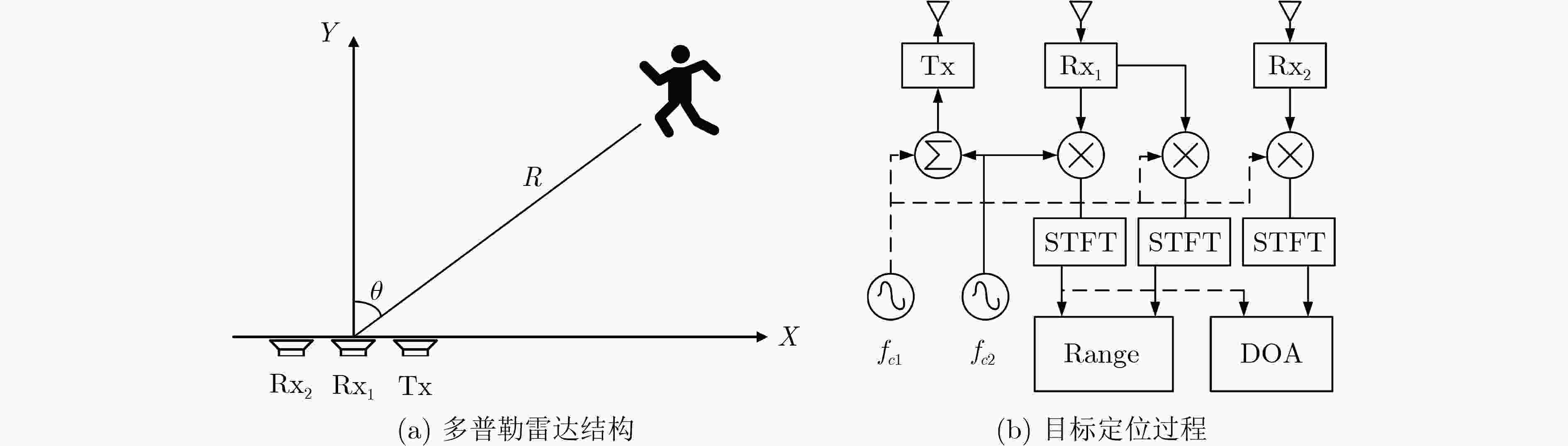
 下载:
下载:
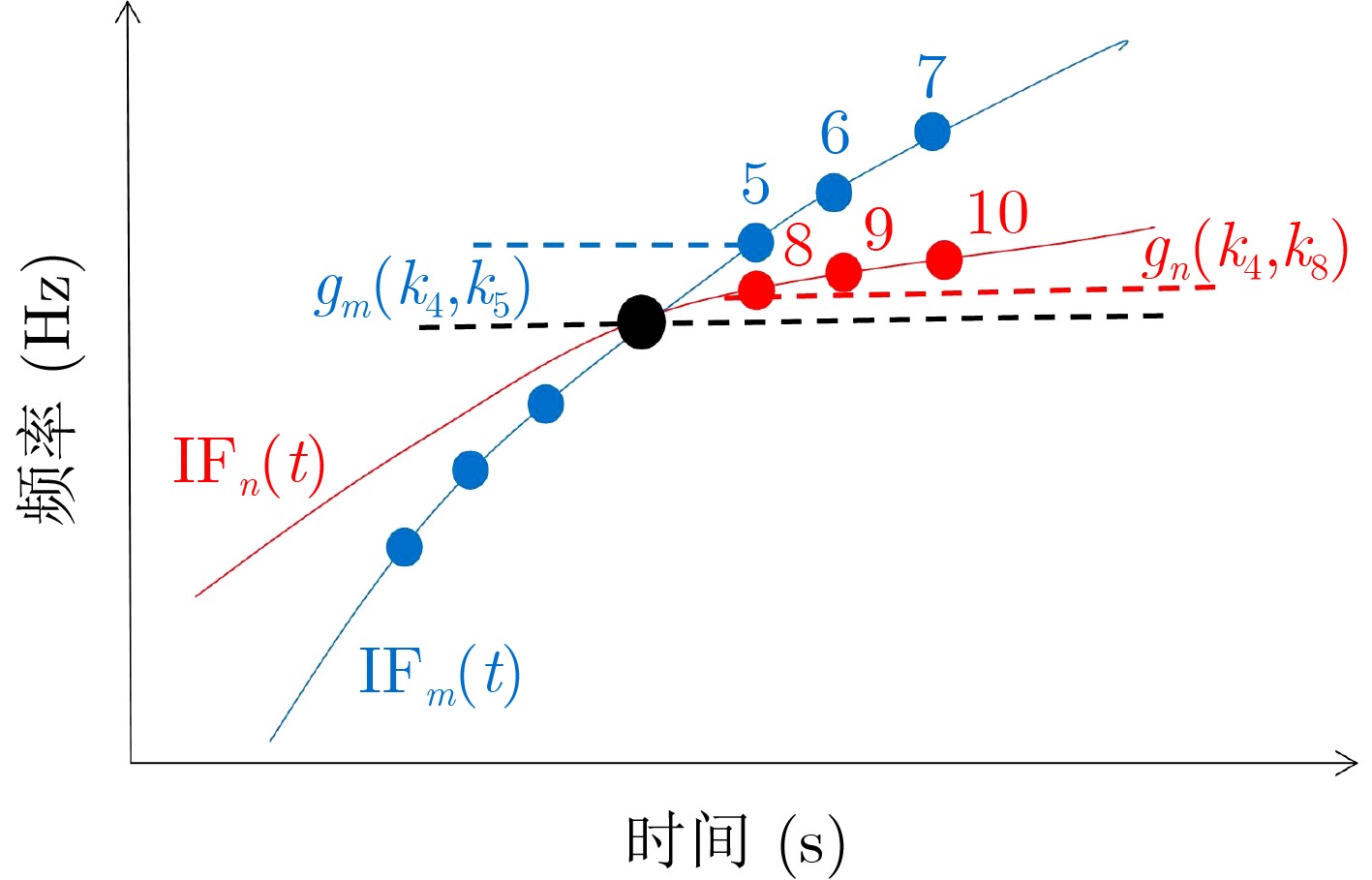

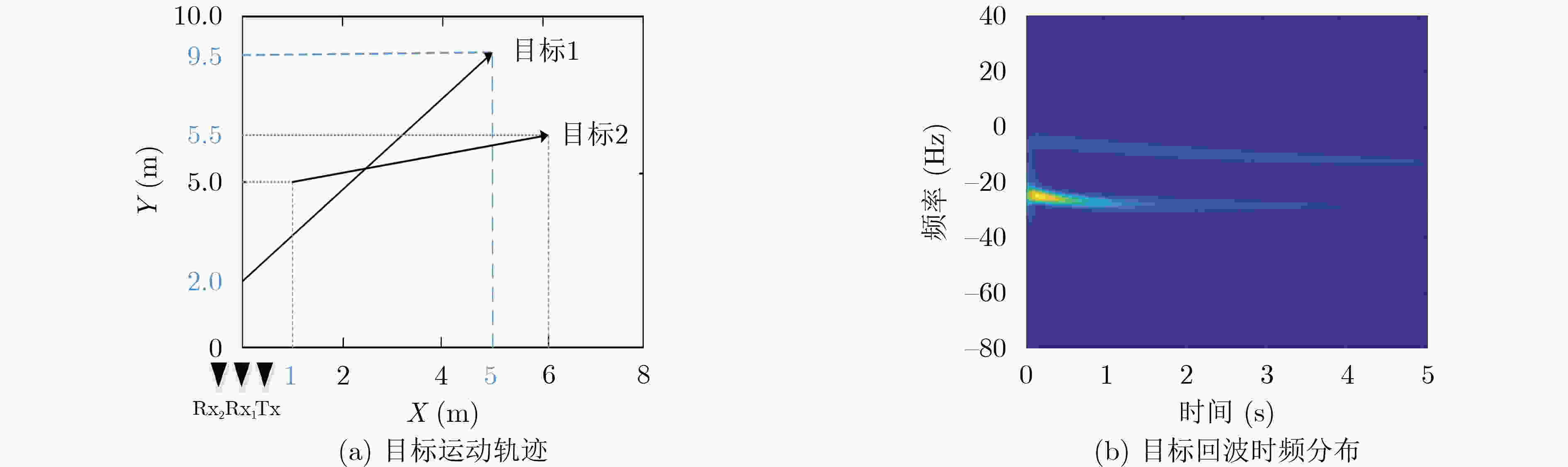
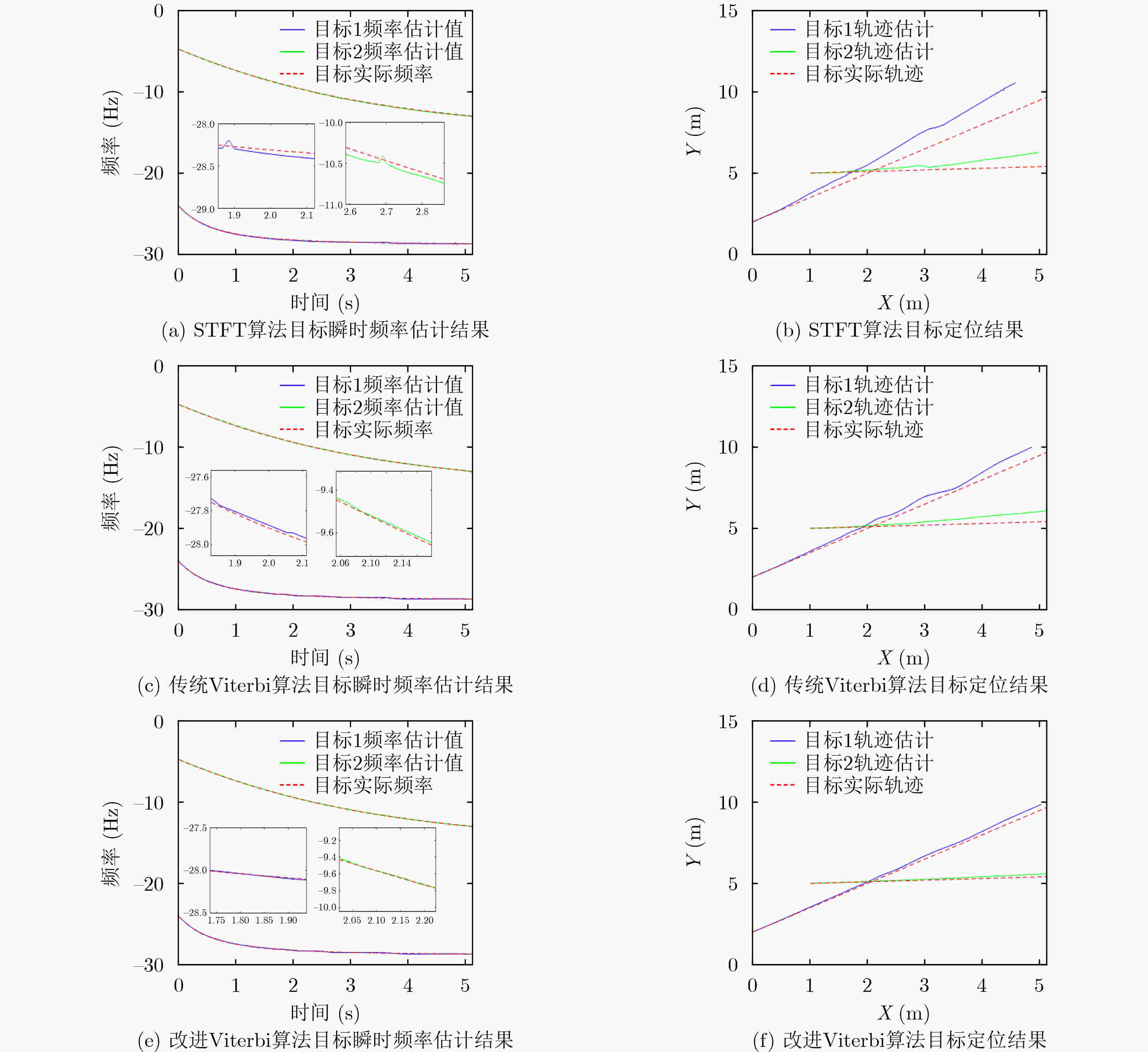


 下载:
下载:
