Multi-constrained Non-negative Matrix Factorization Algorithm Based on Sinkhorn Distance Feature Scaling
-
摘要: 为了减少原始特征对非负矩阵分解(NMF)算法的共适应性干扰,并提高NMF的子空间学习能力与聚类性能,该文提出一种基于Sinkhorn距离特征缩放的多约束半监督非负矩阵分解算法。首先该算法通过Sinkhorn距离对原始输入矩阵进行特征缩放,提高空间内同类数据特征之间的关联性,然后结合样本标签信息的双图流形结构与范数稀疏约束作为双正则项,使分解后的基矩阵具有稀疏特性和较强的空间表达能力,最后,通过KKT条件对所提算法目标函数的进行优化推导,得到有效的乘法更新规则。通过在多个图像数据集以及平移噪声数据上的聚类实验结果对比分析,该文所提算法具有较强的子空间学习能力,且对平移噪声有更强的鲁棒性。Abstract: In order to reduce the co-adaptability interference of the original feature to the Non-negative Matrix Factorization (NMF) algorithm and improve the performance of non-negative matrix factorization subspace learning and clustering performance, a novel multi-constrained semi-supervised non-negative matrix factorization algorithm based on Sinkhorn distance feature scaling is proposed. First, the algorithm is feature-scaled by the Sinkhorn distance to the original input matrix to improve the correlation between features of the same type of data in the space, then, the dual graph manifold structure combined with the sample label information and the norm sparsity constraint are embedded in the model as a dual regular term, so that the decomposed base matrix has sparse characteristics and strong spatial expression ability. Finally, the objective function of the proposed algorithm is optimized by Karush-Kuhn-Tucker (KKT) conditions, and effective multiplication update rules are obtained. Through the comparative analysis of the results of multiple clustering experiments on multiple image data sets and translational noise data, the algorithm proposed in this paper has a strong subspace learning ability and is more robust to translational noise.
-
表 1 基于Sinkhorn距离特征缩放的多约束非负矩阵分解算法S3GNMF (算法1)
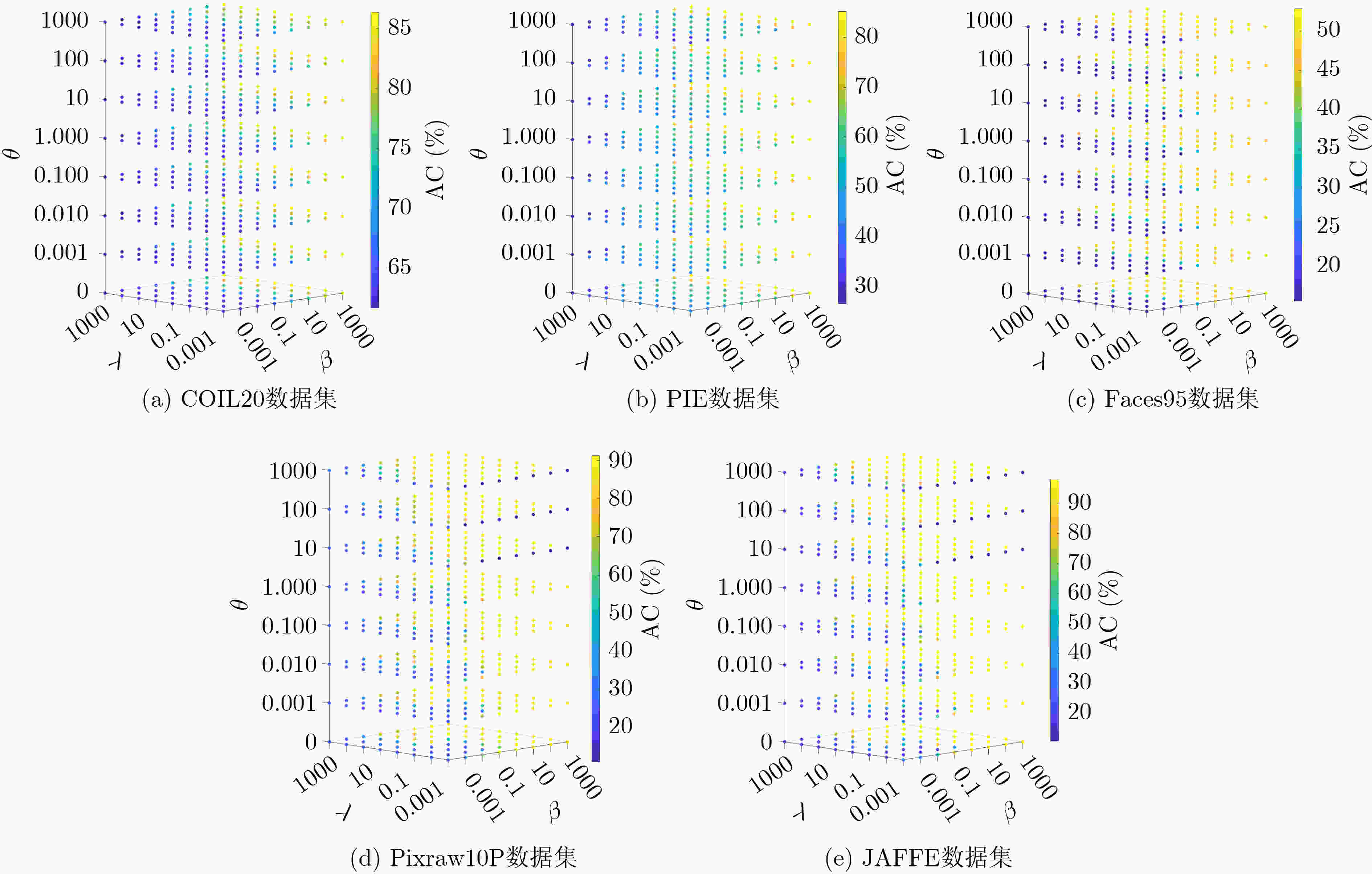
输入:原始矩阵${\boldsymbol{X}}$,聚类数$ k $,流形正则化系数$ \lambda $和$ \beta $,稀疏约束
系数$ \theta $和最大迭代次数$ M $(1)对原始矩阵${\boldsymbol{X}}$进行特征缩放得到矩阵${\boldsymbol{S}}$; (2)随机初始化基矩阵${\boldsymbol{U}}$和辅助矩阵${\boldsymbol{Z}}$;
(3)更新${\boldsymbol{U}}$ ${ {\boldsymbol{u} }_{ij} } \leftarrow { {\boldsymbol{u} }_{ij} }\dfrac{ { { {\left( { {\boldsymbol{SAZ} } + \beta { {\boldsymbol{W} }_{\boldsymbol{U} } }{\boldsymbol{U} } } \right)}_{ij} } } }{ { { {\left( { { {\boldsymbol{UZ} }^{\rm{T} } }{ {\boldsymbol{A} }^{\rm{T} } }{\boldsymbol{AZ} } + \beta { {\boldsymbol{D} }_{\boldsymbol{U} } }{\boldsymbol{U} } + \theta {\boldsymbol{U} } } \right)}_{ij} } } }$;(4)更新${\boldsymbol{Z}}$ ${ {\boldsymbol{z} }_{ij} } \leftarrow { {\boldsymbol{z} }_{ij} }\dfrac{ { { {\left( { { {\boldsymbol{A} }^{\text{T} } }{ {\boldsymbol{S} }^{\text{T} } }{\boldsymbol{U} } + \lambda { {\boldsymbol{A} }^{\text{T} } }{ {\boldsymbol{W} }_{\boldsymbol{Z} } }{\boldsymbol{AZ} } } \right)}_{ij} } } }{ { { {\left( { { {\boldsymbol{A} }^{\text{T} } }{ {\boldsymbol{AZU} }^{\text{T} } }{\boldsymbol{U} } + \lambda { {\boldsymbol{A} }^{\text{T} } }{ {\boldsymbol{D} }_{\boldsymbol{Z} } }{\boldsymbol{AZ} } } \right)}_{ij} } } }$; (5)执行算法步骤(3)和步骤(4) 至最大迭代次数或收敛; 输出:矩阵${\boldsymbol{U}}$和${\boldsymbol{Z}}$ 表 2 各数据集的详细说明
数据集名称 维度大小 类别数 总样本数 数据集类型 COIL20 1024 20 1440 物品 PIE 1024 68 2586 人脸 Faces95 4096 20 400 人脸 Pixraw10P 10000 10 100 人脸 JAFFE 676 10 213 人脸 COIL20-noise 1024 20 1440 人脸+平移噪声 Faces95-noise 4096 20 400 人脸+平移噪声 表 3 各算法在标准数据集上的对比(%)
数据集 NMF CNMF GNMF SNMF SDNMF DSDNMF SODNMF AGNMF ONMF DENMF S3GNMF COIL20 64.2±2.4 69.6±1.6 68.1±1.5 66.9±1.2 71.2±1.0 72.1±1.3 78.9±0.8 73.1±1.1 66.0±1.5 74.7±1.7 84.1±0.9 77.0±1.4 79.8±1.3 80.8±1.0 71.8±2.0 78.6±1.4 79.7±0.8 86.1±1.5 81.0±0.6 70.9±2.2 82.6±1.7 91.6±1.3 PIE 71.3±0.7 68.8±0.8 72.4±0.9 71.9±0.8 74.6±0.8 75.2±0.6 79.3±1.8 75.8±1.1 74.1±1.5 77.2±1.4 81.5±0.8 67.9±0.7 70.7±0.8 80.5±0.9 72.8±0.8 82.1±0.5 81.2±0.7 85.3±0.5 82.4±0.6 76.0±2.0 84.1±1.8 91.8±0.8 Faces95 43.7±1.2 48.6±1.7 50.2±2.3 49.5±1.8 51.2±2.0 50.6±1.8 53.9±1.5 52.2±1.1 49.2±1.1 53.6±0.9 55.1±1.7 50.8±0.6 57.0±1.3 57.7±1.5 55.0±1.3 60.7±1.2 58.1±1.1 60.7±0.8 60.3±1.0 55.3±1.0 60.1±1.6 62.3±1.1 Pixraw10P 68.7±1.8 80.4±1.7 87.4±2.3 71.4±1.1 83.7±2.4 84.0±2.0 89.0±3.6 84.4±2.0 76.3±2.4 84.3±2.9 90.8±3.8 73.8±1.5 83.8±1.2 88.0±1.4 73.7±1.6 84.0±1.6 84.7±1.8 89.7±2.9 86.0±1.8 78.7±1.6 86.0±2.7 93.8±0.7 JAFFE 66.2±1.8 81.1±2.7 82.8±1.2 76.2±0.8 80.1±1.0 80.4±0.8 90.8±1.9 81.4±1.5 77.5±1.2 90.1±0.5 98.1±0.2 68.9±1.5 82.8±1.9 84.0±1.4 78.0±0.6 81.7±1.3 82.0±0.8 92.1±1.4 83.7±1.3 80.0±1.1 88.7±0.6 97.4±0.4 表 4 各算法在平移噪声COIL20数据集上的对比(%)
$ \omega $ NMF CNMF GNMF SNMF SDNMF DSDNMF SODNMF AGNMF ONMF DENMF S3GNMF 1 63.2±2.2 67.6±1.2 69.0±1.5 67.4±1.5 72.3±1.5 74.1±1.8 75.1±1.2 71.7±1.4 65.7±2.2 72.7±2.7 87.2±2.1 75.0±1.4 77.2±1.3 80.5±1.1 70.5±1.3 79.3±1.1 79.9±0.9 84.0±1.1 78.8±0.7 68.1±1.4 74.7±1.9 94.6±0.5 2 52.1±2.3 55.2±1.5 57.7±1.3 56.8±1.6 68.6±1.8 70.1±2.2 63.4±1.6 62.7±1.6 54.0±2.7 61.8±2.6 73.2±2.5 66.7±1.6 69.1±1.5 75.7±1.2 73.9±1.4 80.0±1.5 82.6±1.5 76.1±1.2 75.5±0.8 71.7±1.4 74.5±1.3 85.5±0.9 3 49.8±1.8 50.0±1.3 58.2±1.1 55.6±1.8 60.4±1.9 58.8±2.2 57.2±1.7 56.6±2.0 54.9±2.0 55.0±2.3 63.8±1.9 58.8±0.9 61.9±1.6 69.8±1.1 60.7±1.6 73.4±0.9 73.1±1.3 70.9±0.9 68.4±1.1 60.4±1.4 70.1±2.1 80.8±0.6 4 43.5±1.9 46.7±2.4 48.9±1.6 47.3±2.0 52.5±2.3 53.3±2.5 51.8±1.7 50.9±2.3 47.1±2.1 51.9±1.9 57.6±2.2 55.2±1.1 58.0±1.6 62.2±1.2 60.8±1.2 70.9±0.6 71.3±1.1 65.9±0.8 63.0±1.4 60.4±1.5 64.7±1.7 74.7±0.8 表 5 各算法在平移噪声Faces95数据集上的对比(%)
$ \omega $ NMF CNMF GNMF SNMF SDNMF DSDNMF SODNMF AGNMF ONMF DENMF S3GNMF 1 45.1±0.7 46.2±2.2 49.6±1.8 48.2±1.2 54.1±2.1 53.8±2.5 49.3±1.4 48.2±1.3 47.1±1.8 48.8±1.7 53.4±1.3 53.7±0.6 58.6±1.8 60.3±1.5 55.9±0.9 65.8±1.7 62.7±1.2 55.2±1.7 58.4±1.8 53.4±1.6 58.0±1.4 63.9±0.8 2 44.1±1.0 43.1±1.7 45.6±1.3 43.5±1.2 48.9±2.0 49.2±2.1 46.9±1.3 46.2±1.1 42.9±1.9 47.2±1.3 53.2±0.6 51.8±0.7 50.2±0.8 53.1±1.1 49.9±0.6 58.1±1.7 59.3±1.5 50.2±0.7 49.7±1.2 49.1±1.2 50.6±1.7 62.5±0.7 3 38.5±1.1 37.9±1.3 41.8±1.5 38.5±1.1 45.8±1.7 47.3±1.9 43.2±1.7 42.9±2.2 38.9±2.2 44.2±1.5 49.8±1.5 45.1±0.8 43.7±0.7 44.7±1.1 45.9±0.6 53.1±1.3 55.7±1.3 46.8±0.9 46.4±1.8 45.4±1.8 49.4±2.0 59.9±1.0 4 34.1±1.2 33.7±1.5 38.3±1.7 34.2±1.2 38.9±1.6 39.4±1.7 39.9±1.7 38.5±1.8 34.5±1.8 40.1±1.6 43.5±1.3 40.4±1.1 40.0±0.9 45.9±0.8 39.7±0.5 47.5±1.1 48.0±0.9 47.1±0.9 46.2±0.9 39.2±1.3 47.3±1.9 53.4±0.7 表 6 S2GNMF与S3GNMF的聚类效果对比(%)
数据集 PIE Pixraw10P JAFFE COIL20 COIL20
($ \omega $=2)COIL20
($ \omega $=4)Faces95 Faces95
($ \omega $=2)Faces95
($ \omega $=4)S2GNMF 77.6±1.1 83.7±3.7 90.7±0.7 81.5±1.4 69.0±2.9 55.3±2.0 51.0±2.2 48.7±1.1 38.3±0.9 90.2±0.3 85.4±1.2 92.9±0.8 89.9±0.4 85.1±0.6 72.1±1.1 61.8±1.0 58.6±0.6 48.2±0.6 S3GNMF 81.5±0.8 90.8±3.8 98.1±0.2 84.1±0.9 73.2±2.5 57.6±2.2 55.1±1.7 53.2±0.6 43.5±1.3 91.8±0.8 93.8±0.7 97.4±0.4 91.6±1.3 85.5±0.9 74.7±0.8 62.3±1.1 62.5±0.7 53.4±0.7 表 7 各算法在不同数据集的运算速度对比(s)
数据集 NMF CNMF GNMF SNMF SDNMF DSDNMF SODNMF AGNMF ONMF DENMF S3GNMF COIL20 0.16 1.17 0.24 0.14 161.52 165.94 0.54 26.74 0.21 2.82 1.25 PIE 0.54 2.33 0.69 0.46 328.17 340.75 1.38 40.88 0.69 7.01 2.61 Faces95 0.08 0.65 0.13 0.07 108.41 132.67 0.38 20.62 0.23 3.53 0.43 Pixraw10P 0.14 1.02 0.19 0.14 138.45 155.90 0.41 37.61 0.12 1.67 0.29 JAFFE 0.04 0.41 0.08 0.03 82.07 94.74 0.20 17.84 0.07 1.42 0.17 -
[1] 钱智明, 钟平, 王润生. 基于图正则化与非负组稀疏的自动图像标注[J]. 电子与信息学报, 2015, 37(4): 784–790. doi: 10.11999/JEIT141282QIAN Zhiming, ZHONG Ping, and WANG Runsheng. Automatic image annotation via graph regularization and non-negative group sparsity[J]. Journal of Electronics &Information Technology, 2015, 37(4): 784–790. doi: 10.11999/JEIT141282 [2] 刘正, 张国印, 陈志远. 基于特征加权和非负矩阵分解的多视角聚类算法[J]. 电子学报, 2016, 44(3): 535–540. doi: 10.3969/j.issn.0372-2112.2016.03.006LIU Zheng, ZHANG Guoyin, and CHEN Zhiyuan. A Multiview clustering algorithm based on feature weighting and non-negative matrix factorization[J]. Acta Electronica Sinica, 2016, 44(3): 535–540. doi: 10.3969/j.issn.0372-2112.2016.03.006 [3] 马源培, 杨卓璇, 李慧嘉. 结合Bass模型和LTV的创新产品扩散预测[J]. 聊城大学学报:自然科学版, 2020, 33(4): 26–32.MA Peiyuan, YANG Zhuoxuan, and LI Huijia. Innovative product diffusion forecasting combined bass model and LTV[J]. Journal of Liaocheng University:Natural Science Edition, 2020, 33(4): 26–32. [4] JIA Yuheng, KWONG S, HOU Junhui, et al. Semi-supervised non-negative matrix factorization with dissimilarity and similarity regularization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(7): 2510–2521. [5] 邱飞岳, 陈博文, 陈铁明, 等. 稀疏诱导流形正则化凸非负矩阵分解算法[J]. 通信学报, 2020, 41(5): 84–95. doi: 10.11959/j.issn.1000-436x.2020064QIU Feiyue, CHEN Bowen, CHEN Tieming, et al. Sparsity induced convex nonnegative matrix factorization algorithm with manifold regularization[J]. Journal on Communications, 2020, 41(5): 84–95. doi: 10.11959/j.issn.1000-436x.2020064 [6] 陈善学, 刘荣华. 基于子空间结构正则化的L21非负矩阵分解高光谱解混[J]. 电子与信息学报, 2022, 44(5): 1704–1713. doi: 10.11999/JEIT210232CHEN Shanxue and LIU Ronghua. L21 Nonnegative matrix factorization based on subspace structure regularization for hyperspectral unmixing[J]. Journal of Electronics &Information Technology, 2022, 44(5): 1704–1713. doi: 10.11999/JEIT210232 [7] CHEN Wensheng, LIU Jingmin, PAN Binbin, et al. Face recognition using nonnegative matrix factorization with fractional power inner product kernel[J]. Neurocomputing, 2019, 348: 40–53. doi: 10.1016/j.neucom.2018.06.083 [8] YANG Zhen, CHEN Weitong, and HUANG Jian. Enhancing recommendation on extremely sparse data with blocks-coupled non-negative matrix factorization[J]. Neurocomputing, 2018, 278: 126–133. doi: 10.1016/j.neucom.2017.04.080 [9] SHIRDHONKAR S and JACOBS D W. Approximate earth mover’s distance in linear time[C]. 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, USA, 2008: 1–8. [10] CAI Deng, HE Xiaofei, HAN Jiawei, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1548–1560. doi: 10.1109/TPAMI.2010.231 [11] QIAN Wei, HONG Bin, CAI Deng, et al. Non-negative matrix factorization with Sinkhorn distance[C]. The 25th International Joint Conference on Artificial Intelligence, New York, USA, 2016: 1960–1966. [12] HOYER P O. Non-negative matrix factorization with sparseness constraints[J]. Journal of Machine Learning Research, 2004, 5(9): 1457–1469. [13] LIU Haifeng, WU Zhaohui, LI Xuelong, et al. Constrained nonnegative matrix factorization for image representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1299–1311. doi: 10.1109/TPAMI.2011.217 [14] LI Dong, ZHANG Baoxian, YAO Zheng, et al. A feature scaling based k-nearest neighbor algorithm for indoor positioning system[C]. 2014 IEEE Global Communications Conference, Austin, USA, 2014: 436–441. [15] JIMÉNEZ-CORDERO A and MALDONADO S. Automatic feature scaling and selection for support vector machine classification with functional data[J]. Applied Intelligence, 2021, 51(1): 161–184. [16] RUBNER Y, TOMASI C, and GUIBAS L J. The earth mover’s distance as a metric for image retrieval[J]. International Journal of Computer Vision, 2000, 40(2): 99–121. doi: 10.1023/A:1026543900054 [17] CUTURI M. Sinkhorn distances: Lightspeed computation of optimal transport[C]. The 26th International Conference on Neural Information Processing Systems, Lake Tahoe, Spain, 2013: 2292–2300. [18] FROGNER C, ZHANG Chiyuan, MOBAHI H, et al. Learning with a Wasserstein loss[C]. The 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2015: 2053–2061. [19] HUANG Shudong, WANG Hongjun, LI Tao, et al. Robust graph regularized nonnegative matrix factorization for clustering[J]. Data Mining and Knowledge Discovery, 2018, 32(2): 483–503. doi: 10.1007/s10618-017-0543-9 [20] XU Zongben, CHANG Xiangyu, XU Fengmin, et al. L1/2 regularization: A thresholding representation theory and a fast solver[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(7): 1013–1027. doi: 10.1109/TNNLS.2012.2197412 [21] LEE D D and SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788–791. doi: 10.1038/44565 [22] ZHANG Yunmeng, SHU Zhenqiu, ZHANG Jie, et al. Dual Graph regularized NMF with Sinkhorn Distance[C]. The 19th International Symposium on Distributed Computing and Applications for Business Engineering and Science, Xuzhou, China, 2020: 146–149. [23] MENG Yang, SHANG Ronghua, JIAO Licheng, et al. Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints[J]. Engineering Applications of Artificial Intelligence, 2018, 69: 24–35. doi: 10.1016/j.engappai.2017.11.008 [24] ZHANG Lin, LIU Zhonghua, PU Jiexin, et al. Adaptive graph regularized nonnegative matrix factorization for data representation[J]. Applied Intelligence, 2020, 50(2): 438–447. doi: 10.1007/s10489-019-01539-9 [25] CHOI S. Algorithms for orthogonal nonnegative matrix factorization[C]. Proceedings of 2008 IEEE International Joint Conference on Neural Networks, Hong Kong, China, 2008: 1828–1832. [26] WU Wenhui, KWONG S, HOU Junhui, et al. Simultaneous dimensionality reduction and classification via dual embedding regularized nonnegative matrix factorization[J]. IEEE Transactions on Image Processing, 2019, 28(8): 3836–3847. doi: 10.1109/TIP.2019.2907054 [27] LIANG Naiyao, YANG Zuyuan, LI Zhenni, et al. Multi-view clustering by non-negative matrix factorization with co-orthogonal constraints[J]. Knowledge-Based Systems, 2020, 194: 105582. doi: 10.1016/j.knosys.2020.105582 [28] QIU Xiru, CHEN Zhikui, ZHAO Liang, et al. Unsupervised multi-view non-negative for law data feature learning with dual graph-regularization in smart Internet of Things[J]. Future Generation Computer Systems, 2019, 100: 523–530. doi: 10.1016/j.future.2019.05.055 -






 下载:
下载:





 下载:
下载:
