Multi-carrier Index Modulation Based on Prolate Spheroidal Wave Functions with Better Multiple-mode
-
摘要: 围绕如何提高椭圆球面波(PSWFs)多载波调制系统频带利用率,该文在双模PSWFs多载波索引调制解调方法的基础上,引入由额外星座点组成的第3星座图,提出基于优化多重索引的PSWFs多载波索引调制解调方法BIM-MCM-PSWFs。该方法通过对分组后每个子块中子载波的多重排列组合,拓展了信号索引维度,增加了调制符号组合数,实现了双模PSWFs多载波索引调制解调方法中频谱资源的进一步利用,有效提高了系统频带利用率。理论和仿真分析表明,该文所提方法相较于双模PSWFs多载波索引调制解调方法,以适当牺牲误码性能为代价,具有更高的系统频带利用率,当n=9, k=1, m=4时,以误比特率(BER)牺牲了0.70 dB为代价,系统频带利用率(SE)提升了20.1%。Abstract: Focusing on how to improve the system spectral efficiency of Prolate Spheroidal Wave Functions(PSWFs) multi-carrier modulation system, a third constellation composed of additional constellation points on the basis of multi-carrier index modulation based on PSWFs with dual-mode method is introduced in this paper. The Multi-Carrier index Modulation based on PSWFs with Better multIple-Mode (BIM-MCM-PSWFs) is proposed. In this method, the signal index dimension is expanded and the number of modulation symbol combinations is increased through the multiple arrangement and combination of subcarriers in each sub block after grouping. The method proposed in this paper realizes the further utilization of spectrum resources in the multi-carrier index modulation based on PSWFs with dual-mode method, and improves effectively system spectral efficiency. Theoretical and simulation analysis show that, compared with the multi-carrier index modulation based on PSWFs with dual-mode method, the method proposed in this paper has a higher system spectral efficiency at the cost of appropriately sacrificing bit error performance. When n=9, k=1, m=4, Spectral Efficiency(SE) is increased by 20.1% at the expense of 0.70 dB of Bit Error Rate(BER).
-
表 1 n=4, k=3, m=2时BIM-MCM-PSWFs的一种映射方案
比特信号 信号索引 子载波映射 [0,0,0] {3,1,2,2} {$ s_{\rm I} ^{\rm C} (1) $,$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm B} (2) $} [0,0,1] {3,2,1,2} {$ s_{\rm I} ^{\rm C} (1) $,$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm B} (2) $} [0,1,0] {1,3,2,2} {$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm C} (1) $,$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm B} (2) $} [0,1,1] {2,3,1,2} {$ s_{{\rm{\rm I}}} ^{{\rm{\rm B}}} (1) $,$ s_{{\rm{\rm I}}} ^{{\rm{\rm C}}} (1) $,$ s_{{\rm{\rm I}}} ^{{\rm{\rm A}}} (1) $,$ s_{{\rm{\rm I}}} ^{{\rm{\rm B}}} (2) $} [1,0,0] {1,2,3,2} {$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm C} (1) $,$ s_{\rm I} ^{\rm B} (2) $} [1,0,1] {2,1,3,2} {$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm C} (1) $,$ s_{\rm I} ^{\rm B} (2) $} [1,1,0] {1,2,2,3} {$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm B} (2) $,$ s_{\rm I} ^{\rm C} (1) $} [1,1,1] {2,1,2,3} {$ s_{\rm I} ^{\rm B} (1) $,$ s_{\rm I} ^{\rm A} (1) $,$ s_{\rm I} ^{\rm B} (2) $,$ s_{\rm I} ^{\rm C} (1) $} 表 2 不同多载波调制方法系统频带利用率
调制方法 g n k m SE(bit/(s·Hz)) Eb/N0(dB) $\rho $(%) BIM-MCM-PSWFs 10 9 8 4 3.71 12.93 / DM-MCM-PSWFs 10 9 4 / 3.09 12.23 20.1 MCM-PSWFs-SGO-2PAM 9 10 7 / 2.41 11.05 53.9 MCM-PSWFs-SGO-4PAM 10 9 4 / 2.89 14.69 28.4 表 3 不同多载波调制方法系统频带利用率
调制方法 选取PSWFs信号阶数 能量聚集度(%) g n k m SE(bit/(s·Hz)) BIM-MCM-PSWFs 前c-l 阶 99.99 10 9 8 4 3.70 BIM-MCM-PSWFs 后c-l 阶 99.90 10 9 8 4 3.38 表 4 信号索引检测乘法运算量
调制方式 运算量 n k m 乘法次数(B=1.44 MHz) DM-MCM-PSWFs-ML $O\left(ng{2^{\left\lfloor { { {\log }_{\text{2} } }C_n^k} \right\rfloor } }\right)$ 4 2 / 368 9 4 / 5760 BIM-MCM-PSWFs-ML $O\left(ng\left({2}^{\lfloor {\mathrm{log} }_{\text{2} }{C}_{n}^{k}\rfloor }\text{+}{2}^{\lfloor {\mathrm{log} }_{\text{2} }{C}_{k}^{m}\rfloor }\right)\right)$ 4 3 2 552 9 8 4 6480 -
[1] CAI Yunlong, QIN Zhijin, CUI Fangyu, et al. Modulation and multiple access for 5G networks[J]. IEEE Communications Surveys & Tutorials, 2018, 20(1): 629–646. [2] ZHANG Lin, LIANG Yingchang, and XIAO Ming. Spectrum sharing for internet of things: A survey[J]. IEEE Wireless Communications, 2019, 26(3): 132–139. doi: 10.1109/MWC.2018.1800259 [3] HOU Zhanwei, SHE Changyang, LI Yonghui, et al. Prediction and communication co-design for ultra-reliable and low-latency communications[J]. IEEE Transactions on Wireless Communications, 2020, 19(2): 1196–1209. doi: 10.1109/TWC.2019.2951660 [4] BUZZI S, D’ANDREA C, LI Dejian, et al. MIMO-UFMC transceiver schemes for millimeter-wave wireless communications[J]. IEEE Transactions on Communications, 2019, 67(5): 3323–3336. doi: 10.1109/TCOMM.2019.2896122 [5] MICHAILOW N, MATTHÉ M, GASPAR I S, et al. Generalized frequency division multiplexing for 5th generation cellular network[J]. IEEE Transactions on Communications, 2014, 62(9): 3045–3061. doi: 10.1109/TCOMM.2014.2345566 [6] WANG Hongxing, LU Faping, LIU Chuanhui, et al. Frequency domain multi-carrier modulation based on prolate spheroidal wave functions[J]. IEEE Access, 2020, 8: 99665–99680. doi: 10.1109/ACCESS.2020.2997679 [7] 陆发平, 王红星, 刘传辉, 等. 椭圆球面函数频域调制解调方法[J]. 电子与信息学报, 2020, 42(8): 1888–1895. doi: 10.11999/JEIT190642LU Faping, WANG Hongxing, LIU Chuanhui, et al. PSWFs frequency domain modulation and demodulation method[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1888–1895. doi: 10.11999/JEIT190642 [8] KHARE K and GEORGE N. Sampling theory approach to prolate spheroidal wavefunctions[J]. Journal of Physics A:Mathematical and General, 2003, 36(39): 10011–10021. doi: 10.1088/0305-4470/36/39/303 [9] 王红星, 陆发平, 刘传辉, 等. 严格奇偶对称的椭圆球面波函数信号构建与低复杂度检测方法[J]. 中国科学:信息科学, 2020, 50(5): 766–776. doi: 10.1360/SSI-2019-0121WANG Hongxing, LU Faping, LIU Chuanhui, et al. Strict Parity Symmetric prolate spheroidal wave functions Signal construction and low complexity detection method[J]. Scientia Sinica Informationis, 2020, 50(5): 766–776. doi: 10.1360/SSI-2019-0121 [10] BAŞAR E, AYGÖLÜ U, PANAYIRCI E, et al. Orthogonal frequency division multiplexing with index modulation[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5536–5549. doi: 10.1109/TSP.2013.2279771 [11] 王红星, 陆发平, 刘传辉, 等. 基于信号分组优化的椭圆球面波多载波调制解调方法[J]. 中国科学:信息科学, 2021, 51(7): 1168–1182. doi: 10.1360/SSI-2020-0007WANG Hongxing, LU Faping, LIU Chuanhui, et al. Multi-carrier modulation scheme based on prolate spheroidal wave functions with signal grouping optimization[J]. Scientia Sinica Informationis, 2021, 51(7): 1168–1182. doi: 10.1360/SSI-2020-0007 [12] 王红星, 张力凡, 陆发平, 等. 双模椭圆球面波多载波索引调制解调方法[J]. 电子与信息学报, 2022, 44(2): 694–701. doi: 10.11999/JEIT210106WANG Hongxing, ZHANG Lifan, LU Faping, et al. Multi-carrier index modulation based on prolate spheroidal wave functions with dual-mode[J]. Journal of Electronics &Information Technology, 2022, 44(2): 694–701. doi: 10.11999/JEIT210106 [13] WEN Miaowen, BASAR E, LI Qiang, et al. Multiple-mode orthogonal frequency division multiplexing with index modulation[J]. IEEE Transactions on Communications, 2017, 65(9): 3892–3906. doi: 10.1109/TCOMM.2017.2710312 [14] 陆发平, 刘传辉, 康家方. 基于顺序统计量的索引调制信号检测方法[J]. 无线电通信技术, 2019, 45(1): 57–61. doi: 10.3969/j.issn.1003-3114.2019.01.11LU Faping, LIU Chuanhui, and KANG Jiafang. Index modulation signal detection method based on order statistic[J]. Radio Communications Technology, 2019, 45(1): 57–61. doi: 10.3969/j.issn.1003-3114.2019.01.11 [15] 王红星, 陆发平, 刘传辉, 等. 基于广义信号索引的椭圆球面波函数多载波调制解调方法[J]. 中国科学:信息科学, 2021, 51(9): 1524–1539. doi: 10.1360/SSI-2021-0003WANG Hongxing, LU Faping, LIU Chuanhui, et al. Multi-carrier Modulation Scheme Based on Prolate Spheroidal Wave Functions with generalized index modulation[J]. Scientia Sinica Informationis, 2021, 51(9): 1524–1539. doi: 10.1360/SSI-2021-0003 [16] FAN Rui, YU Yajun, and GUAN Yongliang. Generalization of orthogonal frequency division multiplexing with index modulation[J]. IEEE Transactions on Wireless Communications, 2015, 14(10): 5350–5359. doi: 10.1109/TWC.2015.2436925 -





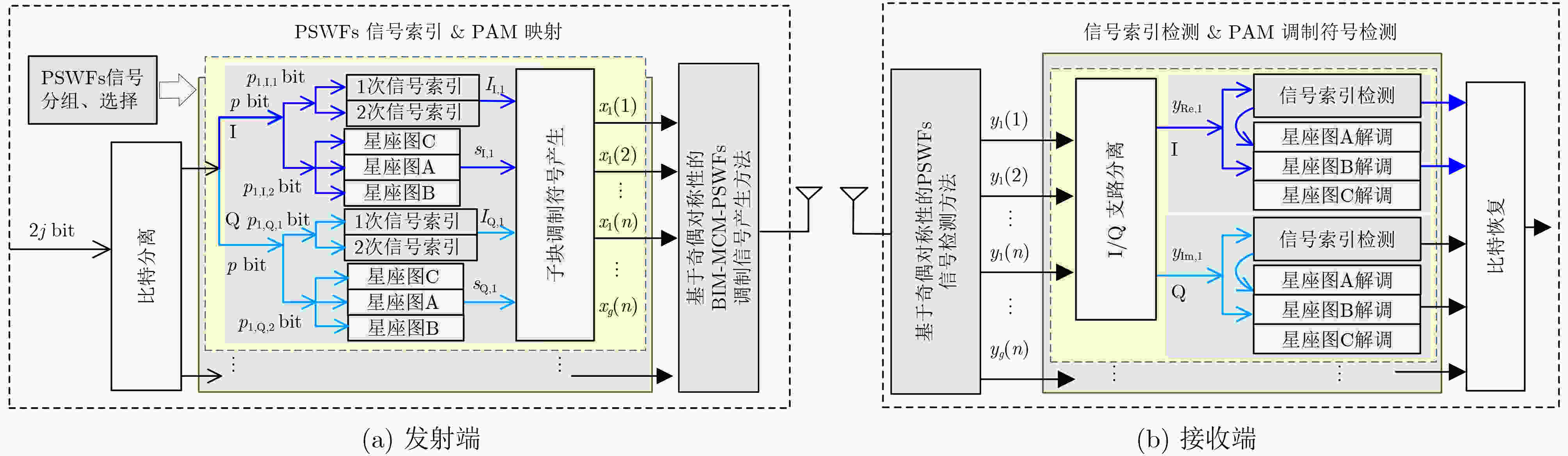
 下载:
下载:
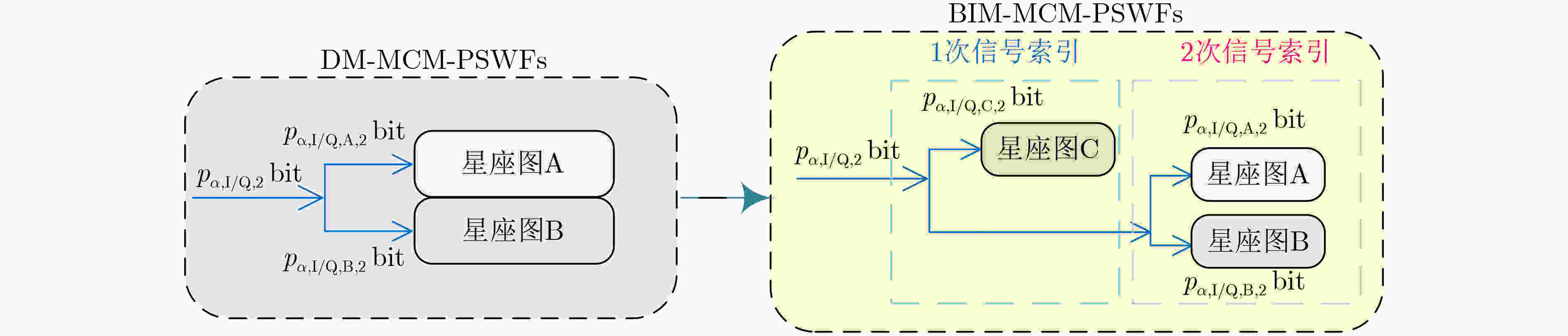
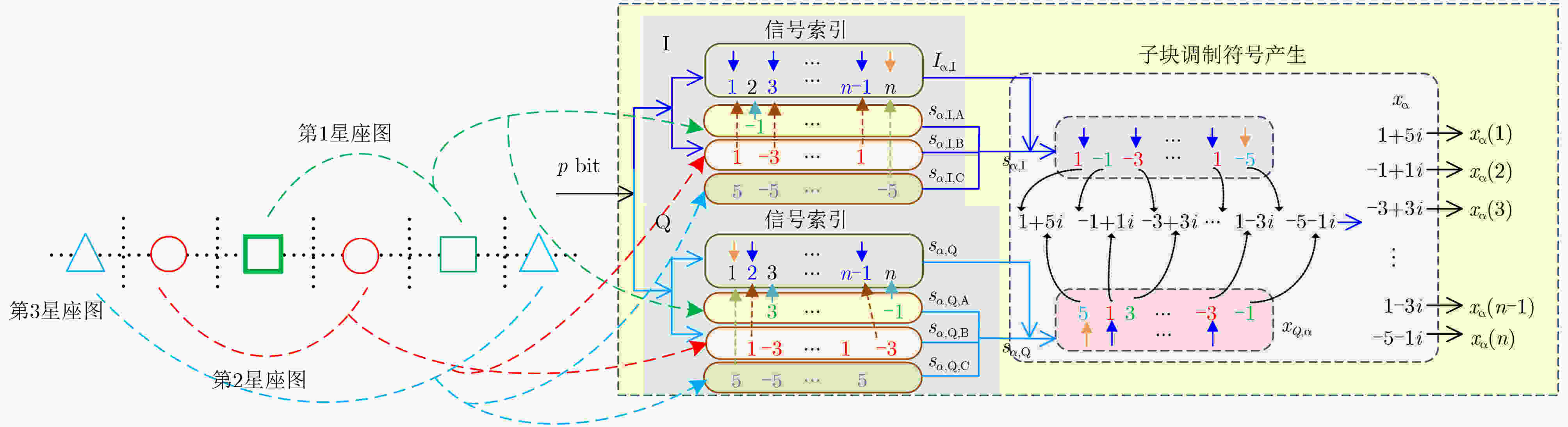

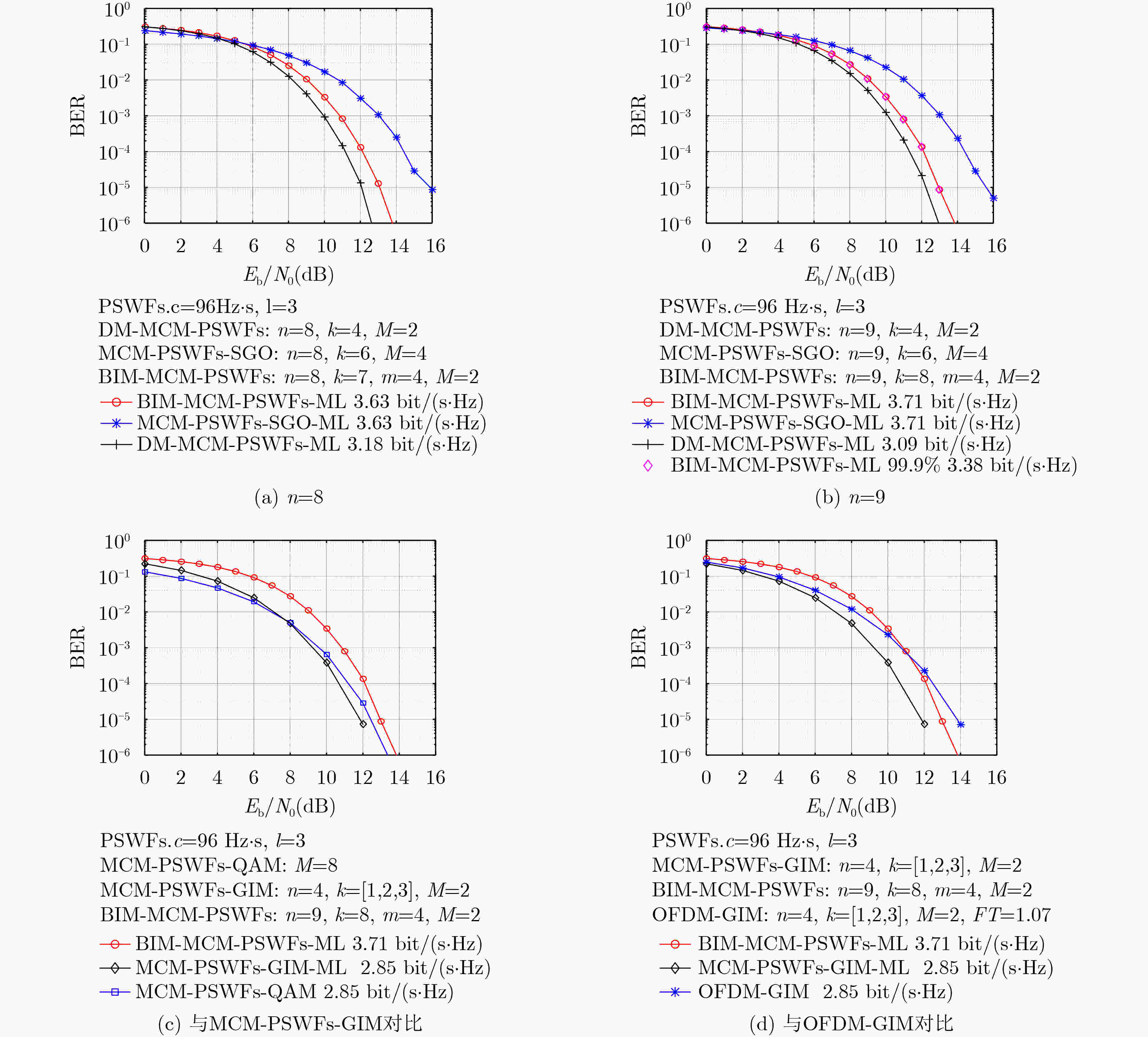


 下载:
下载:
