采用单水听器的匀速圆弧运动直升机三维参数估计算法

张华霞; 孙伟涛; 王惠刚; 荣少巍

doi:10.11999/JEIT210887

采用单水听器的匀速圆弧运动直升机三维参数估计算法

doi: 10.11999/JEIT210887

张华霞¹,
孙伟涛¹,
王惠刚^{1, 2, ,},
荣少巍¹

1.
西北工业大学航海学院西安 710072
2.
西北工业大学深圳研究院深圳 518057

基金项目: 水声对抗技术国家重点实验室项目(JZX7Y201911SY003401)，深圳市科技创新委员会基金(CYJ20190806150003606)，中央高校基本科研业务费专项资金(D5000220158)

详细信息

作者简介:
张华霞：女，博士生，研究方向为阵列信号处理

孙伟涛：男，博士生，研究方向为时频估计、目标检测

王惠刚：男，教授，博士生导师，研究方向为目标检测、参数估计、自适应信息处理

荣少巍：男，博士生，研究方向为目标检测、自适应控制

通讯作者:
王惠刚　wanghg74@nwpu.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 354
- HTML全文浏览量: 179
- PDF下载量: 59
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-27
- 修回日期: 2022-07-07
- 网络出版日期: 2022-07-11
- 刊出日期: 2022-11-14

3D Parameters Estimation of Helicopter with Constant Speed Circular Motion Based on Single Hydrophone

1.
School of Marine Science & Technology, Northwestern Polytechnical University, Xi’an 710072, China
2.
Research & Development Institute in Shenzhen, Northwestern Polytechnical University, Shenzhen 518057, China

Funds: The National Key Laboratory of Science and Technology on Underwater Acoustic Antagonizing (JZX7Y201911SY003401), The Science, Technology and Innovation of Shenzhen Municipality (CYJ20190806150003606), The Fundamental Research Funds for the Central Universities (D5000220158)

摘要

摘要: 针对空中匀速圆弧运动目标激发的水下声信号，该文采用单水听器解决该动目标3维运动参数的估计问题。首先以直升机离散线谱为声源特征，在空气-水介质中建立声源线谱特征在匀速圆弧运动下3维多普勒传播模型。然后根据多普勒频移曲线、声源运动模型以及声线传播几何关系，选取3个时间观测点计算目标多普勒频移，推导了单水听器估计空中匀速圆弧运动声源的3维参数估计算法。最后，通过仿真单水听器所接收的水声信号，验证了该算法估计匀速圆弧运动声源飞行参数的有效性和精度。
- 水下声探测 /
- 多普勒效应 /
- 瞬时频率估计
Abstract: The Three-Dimensional(3D) parameter estimation algorithm of the helicopter with constant speed circular flight from the underwater acoustic data with single hydrophone is proposed. Firstly, the helicopter line spectrum is used as the characteristic of the source, and its 3D Doppler propagation model in two-layer air-water medium is established. Then, the parameters estimation for helicopter in 3D space is derived according to the Doppler frequency shift curve, the sound source motion model and the geometric model of sound propagation. Finally, the effectiveness and accuracy of the algorithm for Doppler signal with the alpha stable noise on single hydrophone is verified.
- Underwater acoustic detection /
- Doppler effect /
- Instantaneous frequency estimation

HTML全文

图 1 空中沿曲线运动的点声源与静止水听器节点的3维图

下载: 全尺寸图片幻灯片

图 2 空中动点声源与静止水听器节点的俯视图

下载: 全尺寸图片幻灯片

图 3 声波传播路径的侧视图

下载: 全尺寸图片幻灯片

图 4 圆弧上选取3个测量点的几何关系图

下载: 全尺寸图片幻灯片

图 5 仿真选取的5组测量点与静止水听器几何示意图

下载: 全尺寸图片幻灯片

图 6 匀速圆弧运动声源的多普勒频移曲线

下载: 全尺寸图片幻灯片

图 7 水听器接收的时域信号

下载: 全尺寸图片幻灯片

图 8 时频曲线的估计结果

下载: 全尺寸图片幻灯片

表 1 参数估计结果

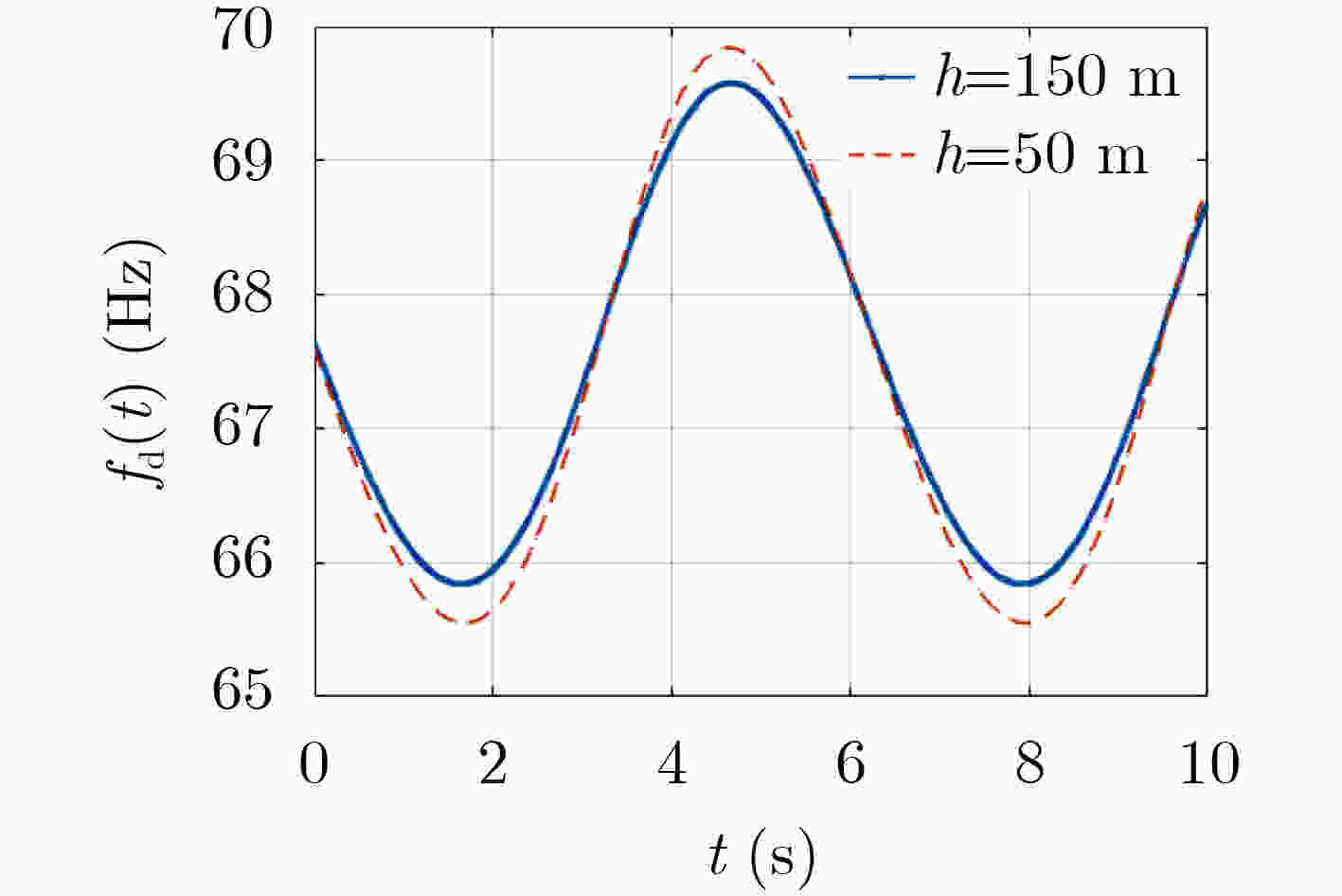
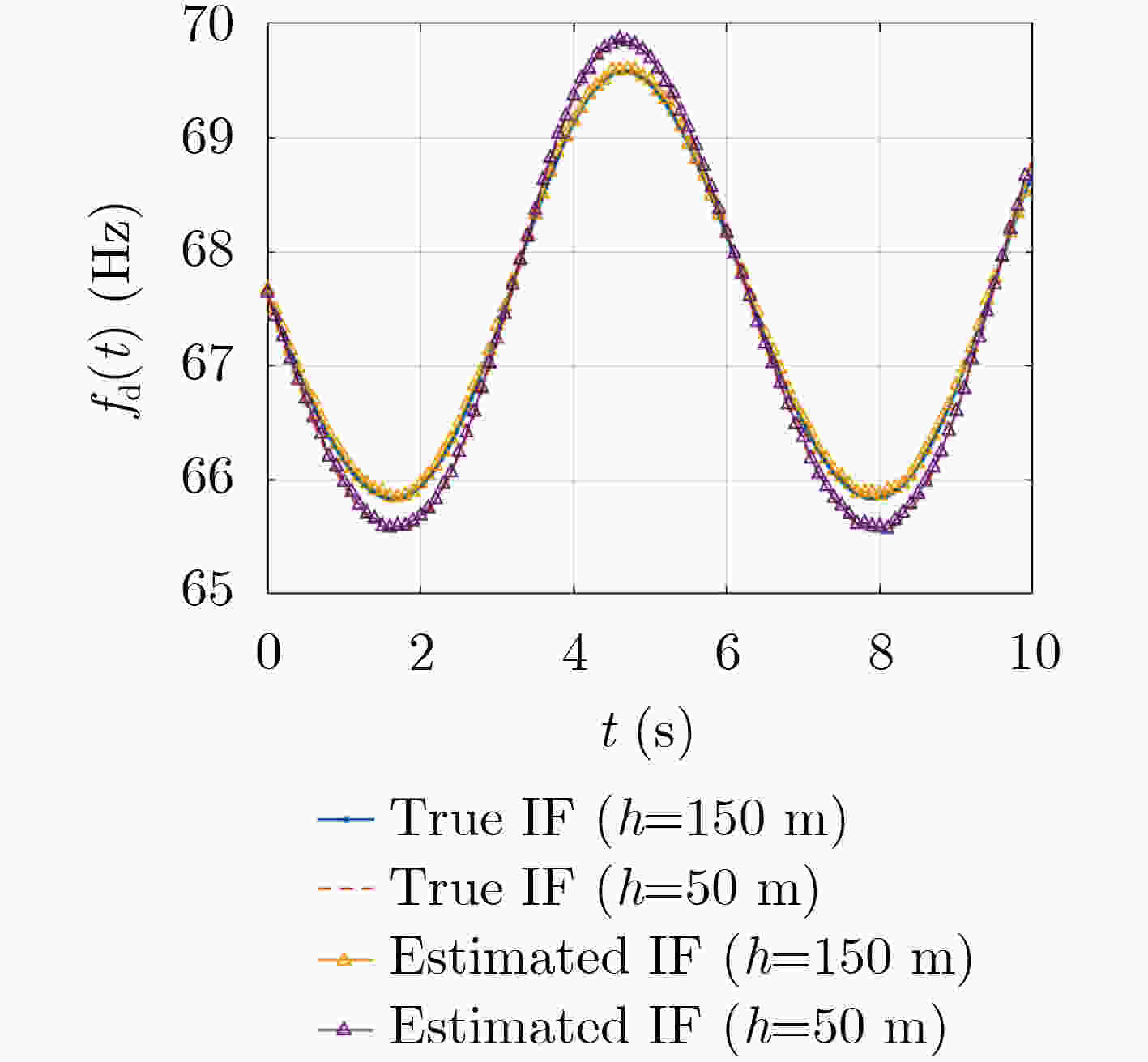
序号	$t$(s)	${f_{\text{d}}}$(Hz)	${f_0}$(Hz)	$v$(m/s)	$h$(m)	$r$(m)
1	$\left. {\begin{array}{*{20}{ll} } { {t_A} = 1.5} \\ { {t_M} = 2} \\ { {t_C} = 2.5} \end{array} } \right\}$	$\left. {\begin{array}{*{20}{lll} } {f\left( { {t_A} } \right) = 67.12} \\ {f\left( { {t_M} } \right) = 67.9} \\ {f\left( { {t_C} } \right) = 68.66} \end{array} } \right\}$	68.7	119.8	145.6	56
2	$\left. {\begin{array}{*{20}{ll} } { {t_A} = 2.7} \\ { {t_M} = 3.2} \\ { {t_C} = 3.7} \end{array} } \right\}$	$ \left. {\begin{array}{*{20}{llll}} {f\left( {{t_A}} \right) = 68.9} \\ {f\left( {{t_M}} \right) = 69.25} \\ {f\left( {{t_C}} \right) = 69.21} \end{array}} \right\} $	68.5	120.1	146.8	61
3	$\left. {\begin{array}{*{20}{ll} } { {t_A} = 4} \\ { {t_M} = 4.2} \\ { {t_C} = 4.4} \end{array} } \right\}$	$ \left. {\begin{array}{*{20}{llll}} {f\left( {{t_A}} \right) = 68.99} \\ {f\left( {{t_M}} \right) = 69.79} \\ {f\left( {{t_C}} \right) = 69.56} \end{array}} \right\} $	67.5	120.8	143.8	58
4	$\left. {\begin{array}{*{20}{ll} } { {t_A} = 3.2} \\ { {t_M} = 3.4} \\ { {t_C} = 3.6} \end{array} } \right\}$	$ \left. {\begin{array}{*{20}{llll}} {f\left( {{t_A}} \right) = 68.25} \\ {f\left( {{t_M}} \right) = 69.3} \\ {f\left( {{t_C}} \right) = 69.24} \end{array}} \right\} $	68.4	125.2	143.1	34
5	$\left. {\begin{array}{*{20}{lll} } { {t_A} = 1.5} \\ { {t_M} = 2} \\ { {t_C} = 2.5} \end{array} } \right\}$	$ \left. {\begin{array}{*{20}{llll}} {f\left( {{t_A}} \right) = 65.58} \\ {f\left( {{t_M}} \right) = 65.66} \\ {f\left( {{t_C}} \right) = 66.24} \end{array}} \right\} $	68.2	120.6	48.6	58

下载: 导出CSV

参考文献(15)

[1]	李浩铭, 鄢社锋, 徐立军, 等. 基于射线声学的水下传感网络静默定位算法[J]. 电子与信息学报, 2021, 43(3): 781–787. doi: 10.11999/JEIT200383 LI Haoming, YAN Shefeng, XU Lijun, et al. A silent location algorithm for underwater sensor network based on ray acoustics[J]. Journal of Electronics &Information Technology, 2021, 43(3): 781–787. doi: 10.11999/JEIT200383
[2]	石海杰, 李京华, 陈刚. 水声探空动目标参数测量方法[J]. 系统工程与电子技术, 2021, 43(1): 11–18. doi: 10.3969/j.issn.1001-506X.2021.01.02 SHI Haijie, LI Jinghua, and CHEN Gang. Hydroacoustic measurement method of airborne moving target parameters[J]. Systems Engineering and Electronics, 2021, 43(1): 11–18. doi: 10.3969/j.issn.1001-506X.2021.01.02
[3]	刘凯悦, 彭朝晖, 张灵珊, 等. 水下对空中声源的运动参数估计[J]. 应用声学, 2020, 39(2): 236–245. doi: 10.11684/j.issn.1000-310X.2020.02.010 LIU Kaiyue, PENG Zhaohui, ZHANG Lingshan, et al. Motion parameters estimation of airborne source from underwater[J]. Journal of Applied Acoustics, 2020, 39(2): 236–245. doi: 10.11684/j.issn.1000-310X.2020.02.010
[4]	王彪, 陈宇, 徐千驰, 等. 非理想条件下基于矢量水听器阵列的一种快速方位估计算法[J]. 电子与信息学报, 2021, 43(3): 745–751. doi: 10.11999/JEIT200541 WANG Biao, CHEN Yu, XU Qianchi, et al. A fast direction estimation algorithm based on vector hydrophone array under non-ideal conditions[J]. Journal of Electronics &Information Technology, 2021, 43(3): 745–751. doi: 10.11999/JEIT200541
[5]	URICK R J. Noise signature of an aircraft in level flight over a hydrophone in the sea[J]. The Journal of the Acoustical Society of America, 1972, 52(3B): 993–999. doi: 10.1121/1.1913206
[6]	FERGUSON B G and SPEECHLEY G C. Acoustic detection and localization of an ASW aircraft by a submarine[J]. The United States Navy Journal of Underwater Acoustics, 1989, 39: 25–41.
[7]	BOLGHASI A, GHADIMI P, and CHEKAB M A F. Low-frequency sound transmission through rough bubbly air–water interface at the sea surface[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2017, 36(4): 319–338. doi: 10.1177/1461348417744295
[8]	PENHALE M and BARNARD A. Direction of arrival estimation in practical scenarios using moving standard deviation processing for localization and tracking with acoustic vector sensors[J]. Applied Acoustics, 2020, 168: 107421. doi: 10.1016/j.apacoust.2020.107421
[9]	LO K W. Flight parameter estimation using instantaneous frequency and direction of arrival measurements from a single acoustic sensor node[J]. The Journal of the Acoustical Society of America, 2017, 141(3): 1332–1348. doi: 10.1121/1.4976091
[10]	张华霞, 王惠刚, 孙伟涛, 等. 采用单水听器匀速直线运动直升机三维参数估计算法[EB/OL]. https://www.researchgate.net.2022.6. ZHANG Huaxia, WANG Huigang, SUN Weitao and RONG Shaowei. 3D Parameters Estimation of Helicopter with Constant Speed Using Single Hydr ophone[EB/OL]. https://www. researchgate.net2022.6.
[11]	SUN Weitao, WANG Huigang, GU Qingyue, et al. Exact frequency estimation in the i. i. d. noise via KL divergence of accumulated power[J]. IEEE Communications Letters, 2021, 25(8): 2574–2578. doi: 10.1109/LCOMM.2021.3077315
[12]	SUN Weitao, WANG Huigang, GU Qingyue, et al. Exact and robust time-frequency estimation via accumulation of phase-difference power on multiple log-sum[J]. Journal of Latex Class Files, 14(8): 1–11.
[13]	LIM J S, PANG H S, and LEE K. Time delay estimation based on log-sum and lp-norm penalized minor component analysis[J]. The Journal of the Acoustical Society of America, 2018, 143(6): 3979–3984. doi: 10.1121/1.5042353
[14]	SHEN Y, Fang J, and LI H. Exact Reconstruction Analysis of Log-Sum Minimization for Compressed Sensing[J]. IEEE Signal Processing Letters, 2013, 20(12): 1223–1226. doi: 10.1109/LSP.2013.2285579
[15]	FAISAL S and DILIP S. Log-sum distance measures and its application to human-activity monitoring and recognition using data from motion sensors[J]. IEEE Sensors Journal, 2017, 17(14): 4520–4533. doi: 10.1109/JSEN.2017.2707921