基于差集矩阵的部分重复码构造

王静; 何亚锦; 雷珂; 刘向阳

doi:10.11999/JEIT210829

基于差集矩阵的部分重复码构造

doi: 10.11999/JEIT210829

王静^1, ,,
何亚锦¹,
雷珂¹,
刘向阳²

1.
长安大学信息工程学院西安 710064
2.
西北工业大学电子信息学院西安 710129

基金项目: 国家自然科学基金 (62001059)，陕西省重点研发计划(2021GY-019)

详细信息

作者简介:
王静：女，博士，教授，研究方向为网络编码、再生码和大数据存储

何亚锦：女，硕士，研究方向为分布式存储、网络编码和部分重复码

雷珂：女，硕士生，研究方向为分布式存储、再生码和部分重复码

刘向阳：男，博士，副教授，研究方向为分布式存储、信号处理

通讯作者:
王静　jingwang@chd.edu.cn

中图分类号: TP301
计量
- 文章访问数: 511
- HTML全文浏览量: 217
- PDF下载量: 70
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-13
- 修回日期: 2022-05-07
- 网络出版日期: 2022-05-11
- 刊出日期: 2022-11-14

Construction of Fractional Repetition Codes Using Difference Set Matrix

1.
School of Information Engineering, Chang’an University, Xi’an 710064, China
2.
School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China

Funds: The National Natural Science Foundation of China (62001059), The Key Research and Development Project of Shaanxi Province (2021GY-019)

摘要

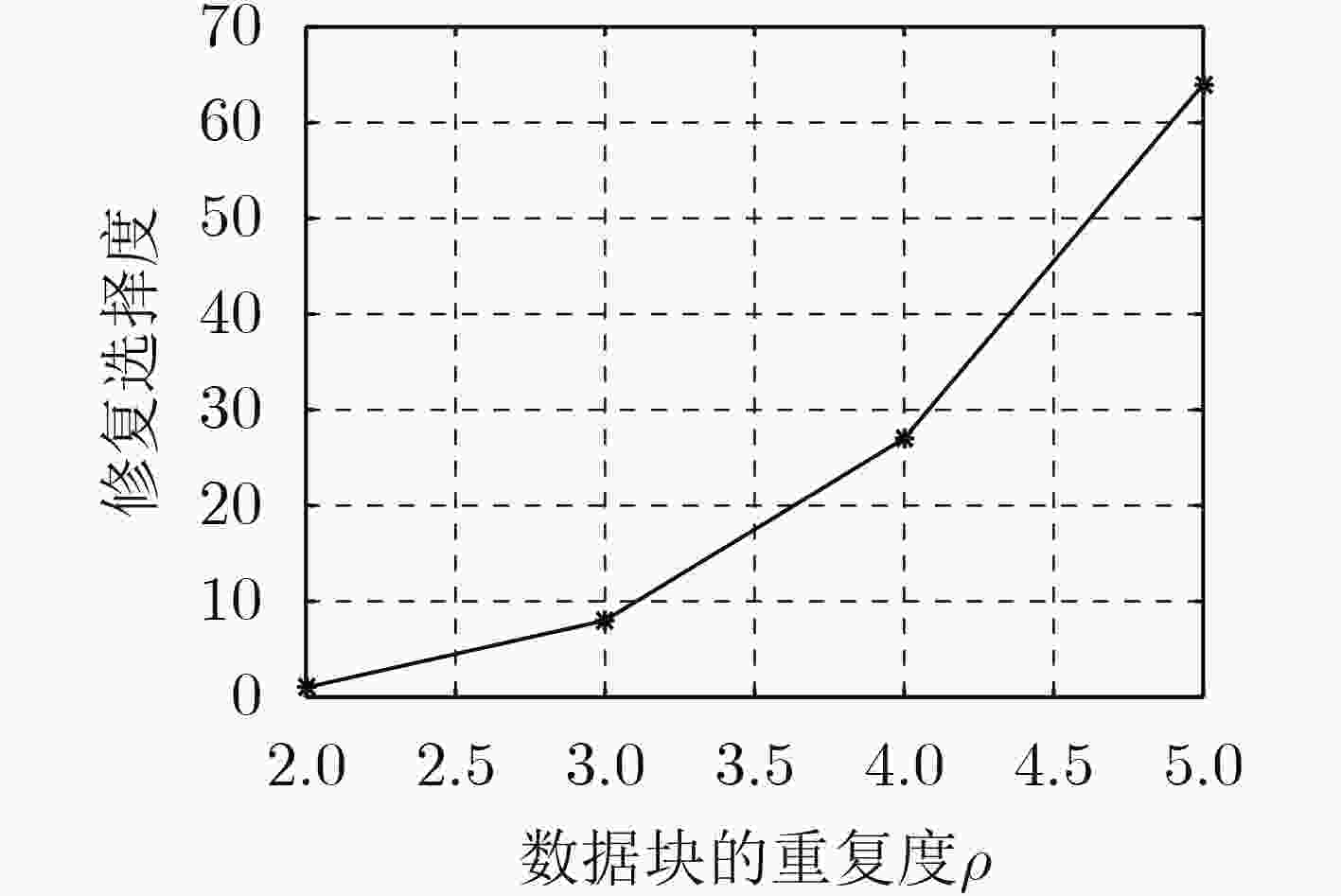
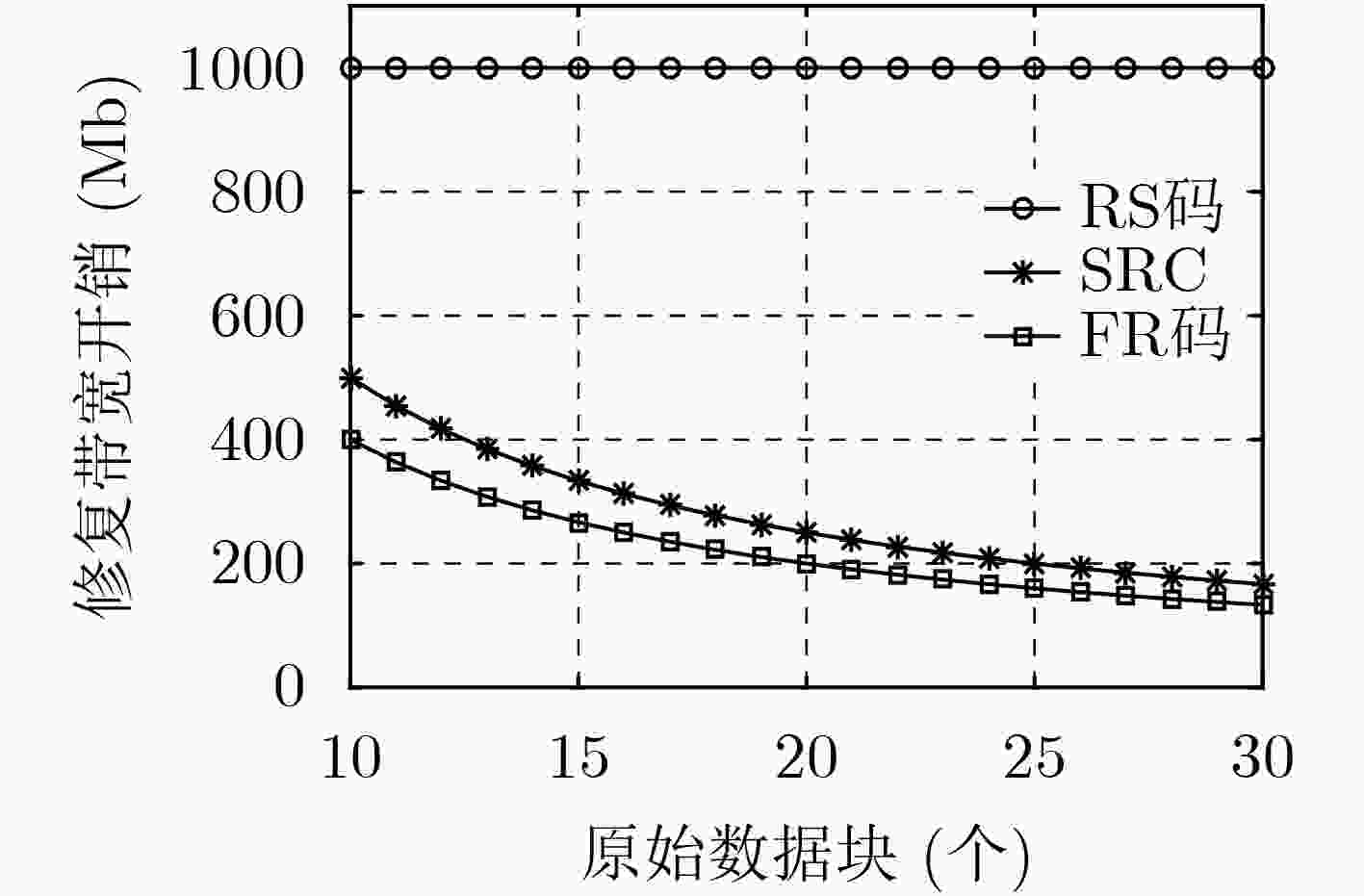
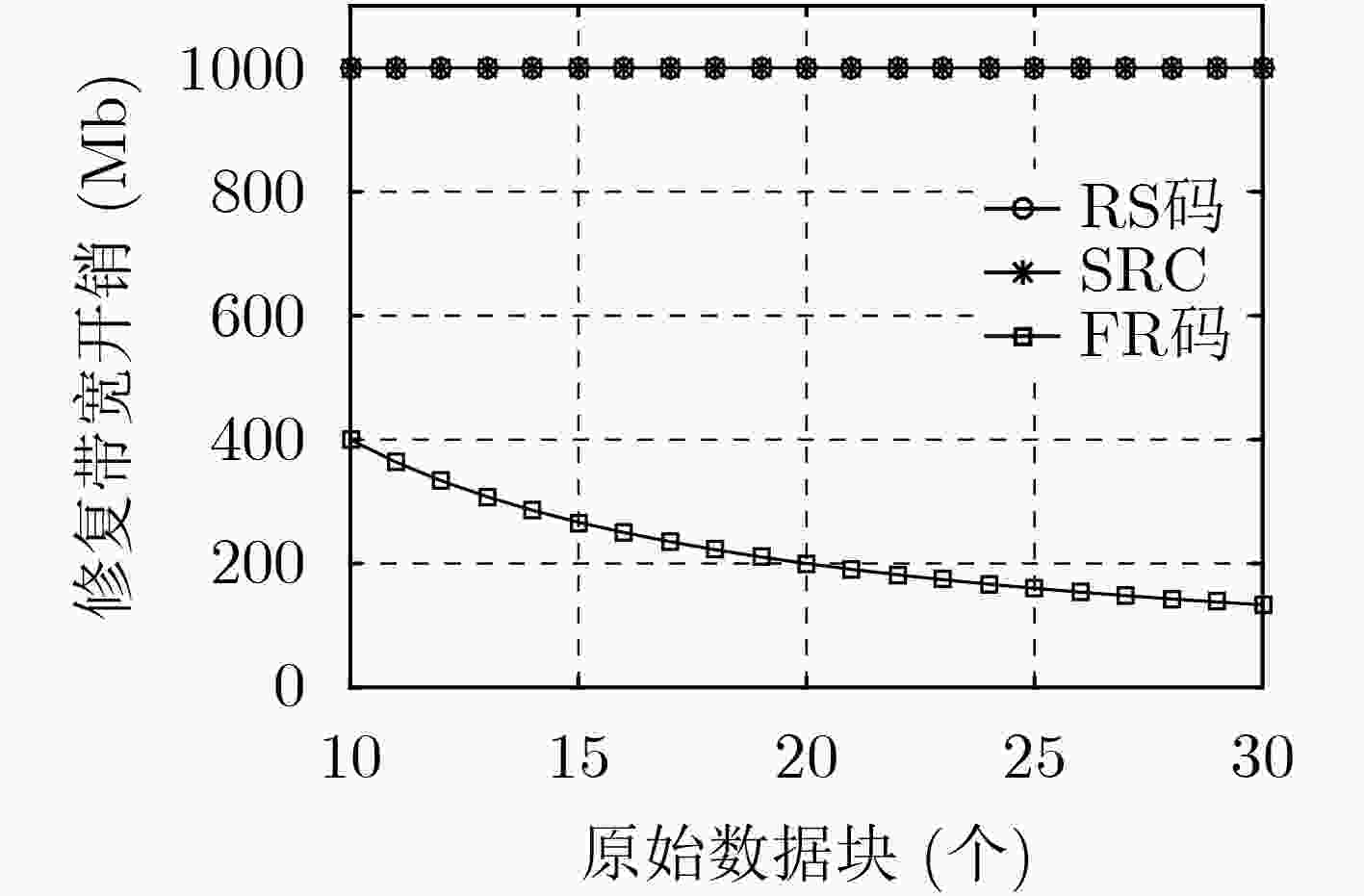
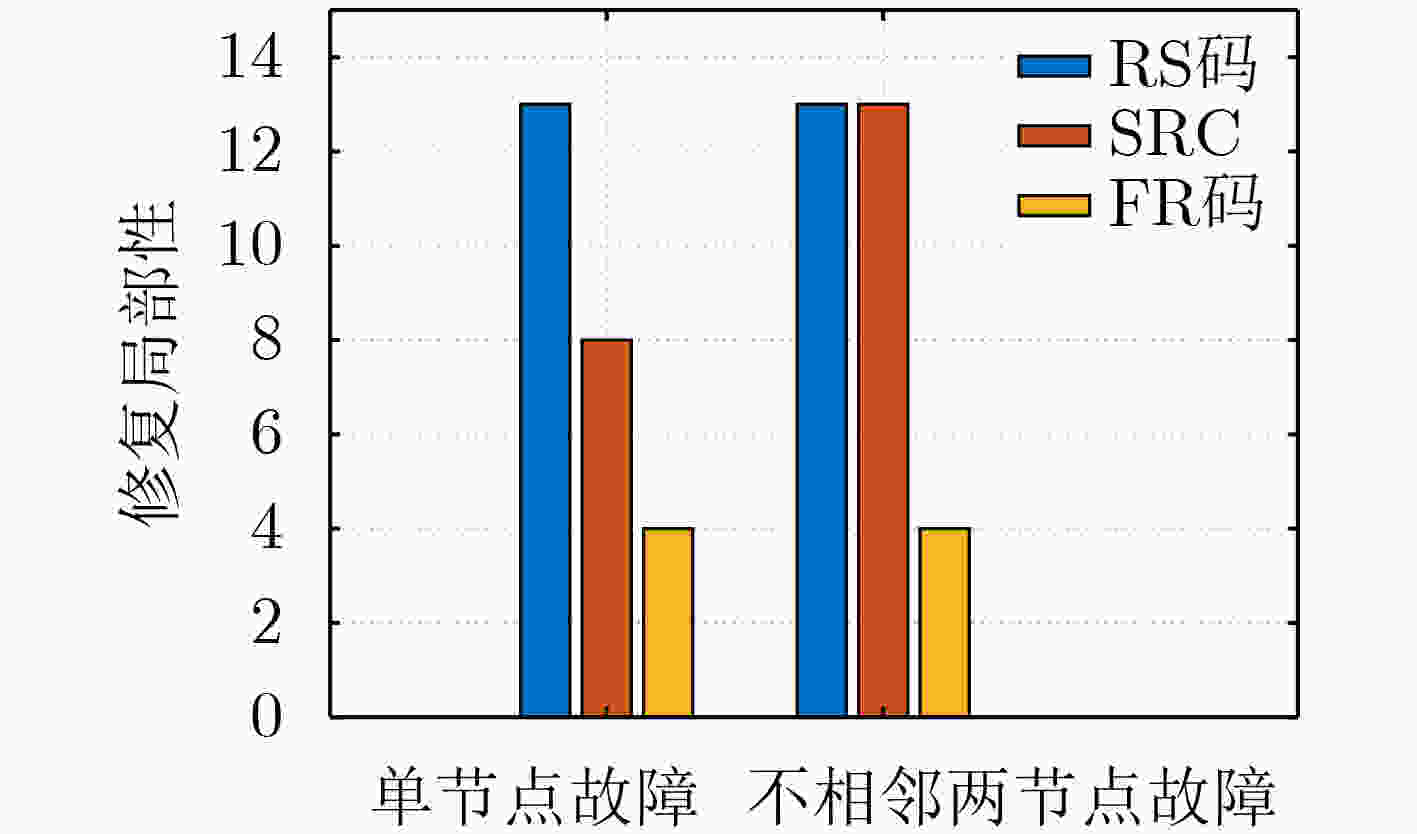
摘要: 针对最小带宽再生码的有效修复问题，该文提出一种基于差集矩阵的部分重复(FR)码的构造算法。利用差集矩阵和克罗内克(Kronecker)和来构造正交排列，根据正交排列每一列取相同元素所在行作为节点的编码块，得到相应的FR码。构造的FR码可以划分成多个平行类，同时还能调整数据块的重复度和节点的存储容量。仿真结果表明，与传统的里德-所罗门(RS)码和简单再生码(SRC)相比，构造的FR码在修复复杂度、修复带宽开销和修复局部性方面具有更好的性能，修复选择度上虽然是基于表格的修复方案，但选择度依旧可以达到很高。
- 部分重复码 /
- 分布式存储系统 /
- 差集矩阵 /
- 正交排列
Abstract: Considering the problem of effective repair of minimum bandwidth regenerating codes, a construction algorithm of Fractional Repetition (FR) codes based on difference set matrix is proposed. The orthogonal array is constructed by using the difference set matrix and Kronecker sum. According to the orthogonal array, each row of the same element is taken as the coding blocks of the node to obtain the corresponding FR codes. As a result, the constructed FR codes can be divided into multiple parallel classes, and at the repetition of the data blocks and the storage capacity of the node can be adjusted. The simulation results show that compared with the traditional Reed-Solomon (RS) codes and Simple Regenerating Codes (SRC), the constructed FR codes have better performance in terms of repair complexity, repair bandwidth overhead, and repair locality. Although the repair selectivity is a table-based repair scheme, the selectivity can still reach high.
- Fractional Repetition(FR) codes /
- Distributed storage systems /
- Difference set matrix /
- Orthogonal array

HTML全文

图 1 节点修复选择度与重复度$ \rho $之间的关系，其中$ \alpha = 3 $

下载: 全尺寸图片幻灯片

图 2 $ \lambda = 1 $时单节点故障修复带宽开销性能对比

下载: 全尺寸图片幻灯片

图 3 $ \lambda = 1 $时两节点故障修复带宽开销性能对比

下载: 全尺寸图片幻灯片

图 4 $ \lambda = 1 $时单节点故障修复局部性性能对比

下载: 全尺寸图片幻灯片

图 5 $ \lambda = 2 $时两节点故障修复局部性性能对比

下载: 全尺寸图片幻灯片

表 1 RS码、SRC和FR码的故障节点修复性能比较

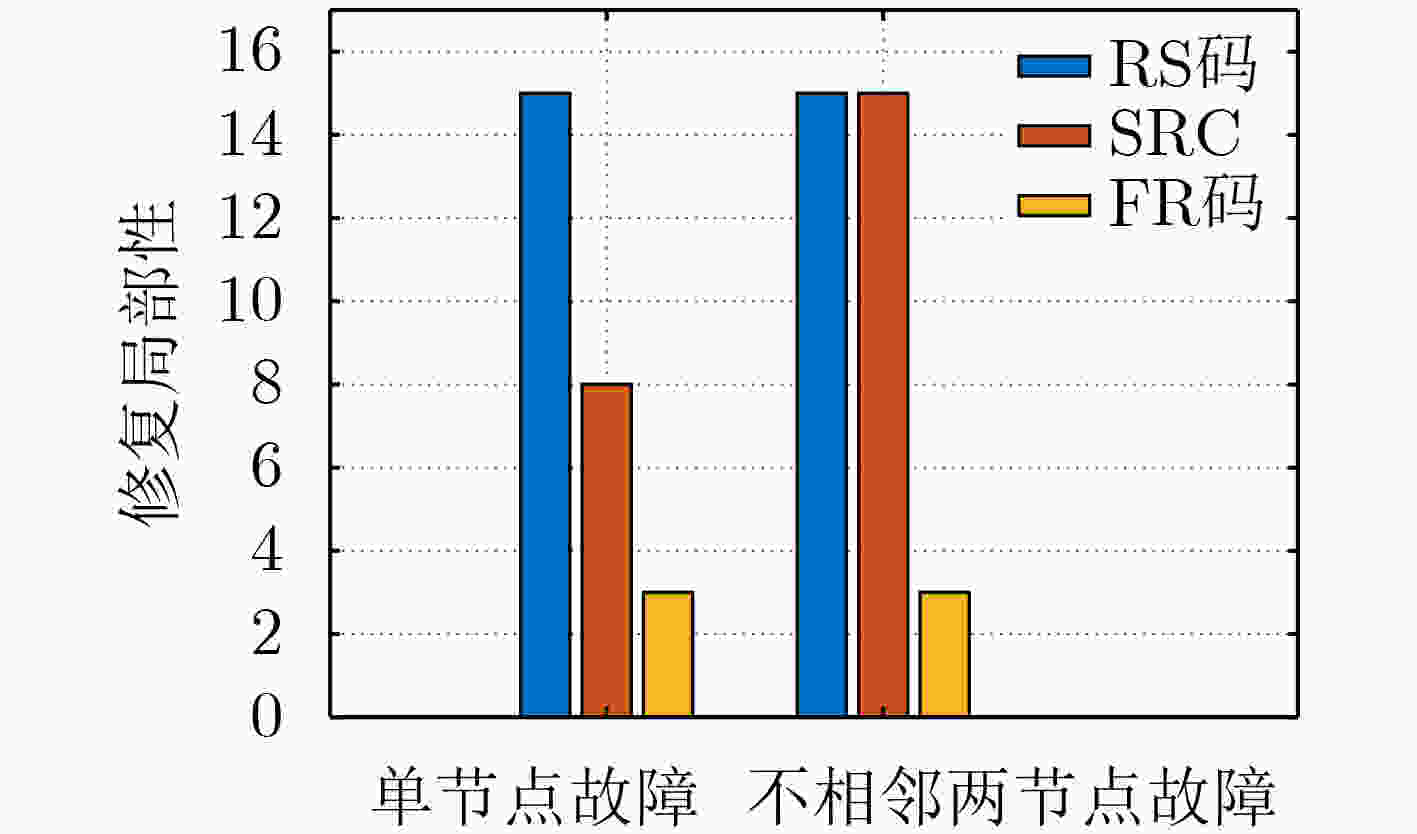
修复带宽开销和修复局部性	编码方案
修复带宽开销和修复局部性	RS码	SRC	FR码
单节点修复带宽开销	M	$(f + 1) M/k$	$ \sqrt {(k + 3)} M/k $
两节点修复带宽开销	M	${\text{2} }{ {(f + 1)M}/ k} 或 M$	$ \sqrt {(k + 3)} M/k $
单节点修复局部性	k	$2f$	$ \sqrt {(k + 3)} $
两节点修复局部性	k	$k$	$ \sqrt {(k + 3)} $

下载: 导出CSV

参考文献(23)

[1]	LIU Ying and VLASSOV V. Replication in distributed storage systems: State of the art, possible directions, and open issues[C]. 2013 International Conference on Cyberenabled Distributed Computing and Knowledge Discovery, Beijing, China, 2013: 225–232.
[2]	LI Jun and LI Baochun. Erasure coding for cloud storage systems: A survey[J]. Tsinghua Science and Technology, 2013, 18(3): 259–272. doi: 10.1109/TST.2013.6522585
[3]	GHEMAWAT S, GOBIOFF H, and LEUNG S T. The Google file system[J]. ACM SIGOPS Operating Systems Review, 2003, 37(5): 29–43. doi: 10.1145/1165389.945450
[4]	HUANG Cheng, SIMITCI H, XU Yikang, et al. Erasure coding in windows azure storage[C]. The 2012 USENIX Annual Technical Conference, Boston, USA, 2012: 15–26.
[5]	SATHIAMOORTHY M, ASTERIS M, PAPAILIOPOULOS D, et al. XORing elephants: Novel erasure codes for big data[J]. Proceedings of the VLDB Endowment, 2013, 6(5): 325–336. doi: 10.14778/2535573.2488339
[6]	DIMAKIS A G, GODFREY P B, WU Yunnan, et al. Network coding for distributed storage systems[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4539–4551. doi: 10.1109/TIT.2010.2054295
[7]	PAPAILIOPOULOS D S and DIMAKIS A G. Distributed storage codes through Hadamard designs[C]. 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 2011: 1230–1234.
[8]	RASHMI K V, SHAH N B, and KUMAR P V. Optimal exact-regenerating codes for distributed storage at the MSR and MBR points via a product-matrix construction[J]. IEEE Transactions on Information Theory, 2011, 57(8): 5227–5239. doi: 10.1109/TIT.2011.2159049
[9]	GUAN Sheng, KAN Haibin, WEN Jie, et al. A new construction of exact-repair MSR codes using linearly dependent vectors[J]. IEEE Communications Letters, 2017, 21(8): 1691–1694. doi: 10.1109/LCOMM.2017.2700862
[10]	GOPALAN P, HUANG Cheng, SIMITCI H, et al. On the locality of codeword symbols[J]. IEEE Transactions on Information Theory, 2012, 58(11): 6925–6934. doi: 10.1109/TIT.2012.2208937
[11]	PAPAILIOPOULOS D S, LUO Jianqiang, DIMAKIS A G, et al. Simple regenerating codes: Network coding for cloud storage[C]. 2012 Proceedings IEEE INFOCOM, Orlando, USA, 2012: 2801–2805.
[12]	WANG Jing, YAN Zhiyuan, LI K C, et al. Local codes with cooperative repair in distributed storage of cyber-physical-social systems[J]. IEEE Access, 2020, 8: 38622–38632. doi: 10.1109/ACCESS.2020.2975577
[13]	HAO Jie, SHUM K W, XIA Shutao, et al. Optimal locally repairable codes for parallel reading[J]. IEEE Access, 2020, 8: 80447–80453. doi: 10.1109/ACCESS.2020.2992188
[14]	EL ROUAYHEB S and RAMCHANDRAN K. Fractional repetition codes for repair in distributed storage systems[C]. 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, USA, 2010: 1510–1517.
[15]	ZHOU Tai, LI Hui, ZHU Bing, et al. STORE: Data recovery with approximate minimum network bandwidth and disk I/O in distributed storage systems[C]. 2014 IEEE International Conference on Big Data, Washington, USA, 2014: 33–38.
[16]	OLMEZ O and RAMAMOORTHY A. Fractional repetition codes with flexible repair from combinatorial designs[J]. IEEE Transactions on Information Theory, 2016, 62(4): 1565–1591. doi: 10.1109/TIT.2016.2531720
[17]	AYDINIAN H and BOCHE H. Fractional repetition codes based on partially ordered sets[C]. 2017 IEEE Information Theory Workshop (ITW), Kaohsiung, China, 2017: 51–55.
[18]	ZHU Bing, SHUM K W, LI Hui, et al. On the duality and file size hierarchy of fractional repetition codes[J]. The Computer Journal, 2019, 62(1): 150–160. doi: 10.1093/comjnl/bxy094
[19]	ZHU Bing, SHUM K W, WANG Weiping, et al. On the optimal minimum distance of fractional repetition codes[C]. GLOBECOM 2020 - 2020 IEEE Global Communications Conference, Taipei, China, 2020: 1–6.
[20]	ZHU Bing, SHUM K W, and LI Hui. Fractional repetition codes with optimal reconstruction degree[J]. IEEE Transactions on Information Theory, 2020, 66(2): 983–994. doi: 10.1109/TIT.2019.2929788
[21]	YU Wenjun, ZHANG Xiande, and GE Gennian. Optimal fraction repetition codes for access-balancing in distributed storage[J]. IEEE Transactions on Information Theory, 2021, 67(3): 1630–1640. doi: 10.1109/TIT.2020.3039901
[22]	SU Yisheng. Optimal pliable fractional repetition codes that are locally recoverable: A bipartite graph approach[J]. IEEE Transactions on Information Theory, 2019, 65(2): 985–999. doi: 10.1109/TIT.2018.2876284
[23]	PRAJAPATI S A, DEB S, and GUPTA M K. On some universally good fractional repetition codes[C]. 2020 International Conference on COMmunication Systems & NETworks (COMSNETS), Bengaluru, India, 2020: 404–411.