椭圆球面波信号Wigner-Ville分布显式渐近求解方法

王红星; 赵乐源; 陆发平; 刘传辉; 康家方

doi:10.11999/JEIT210820

椭圆球面波信号Wigner-Ville分布显式渐近求解方法

doi: 10.11999/JEIT210820

王红星^{1, 2},
赵乐源^{1, 2, ,},
陆发平^{1, 3},
刘传辉^{1, 2},
康家方^{1, 2}

1.
海军航空大学烟台 264001
2.
山东省信号与信息处理重点实验室烟台 264001
3.
中国人民解放军 91206部队青岛 266000

基金项目: 国家自然科学基金(61701518)，山东省“泰山学者”建设工程专项经费基金(ts20081130)

详细信息

作者简介:
王红星：男，教授，研究方向为现代通信系统、非正弦波通信、无线光通信

赵乐源：男，硕士生，研究方向为现代通信系统、非正弦波通信

陆发平：男，博士，研究方向为现代通信系统、非正弦波通信、多载波调制

刘传辉：男，讲师，研究方向为现代通信新技术、非正弦波通信

康家方：男，讲师，研究方向为现代通信新技术、扩频通信、非正弦波通信

通讯作者:
赵乐源　zhaolyvip@163.com

中图分类号: TN911.3
计量
- 文章访问数: 288
- HTML全文浏览量: 212
- PDF下载量: 38
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-12
- 修回日期: 2022-01-03
- 录用日期: 2022-01-05
- 网络出版日期: 2022-01-27
- 刊出日期: 2022-10-19

Explicit and Progressive Solution Method for Wigner-Ville Distribution of Prolate Spheroidal Wave Functions Signal

WANG Hongxing^{1, 2},
ZHAO Leyuan^{1, 2
, ,},
LU Faping^{1, 3},
LIU Chuanhui^{1, 2},
KANG Jiafang^{1, 2}

1.
Naval Aviation University, Yantai 264001, China
2.
Key Laboratory on Signal & Information Processing of Shandong Province, Yantai 264001, China
3.
Unit 91206 of the PLA, Qingdao 266000, China

Funds: The National Natural Science Foundation of China (61701518), The Special Foundation Project of Taishan Scholar of Shandong Province (ts20081130)

摘要

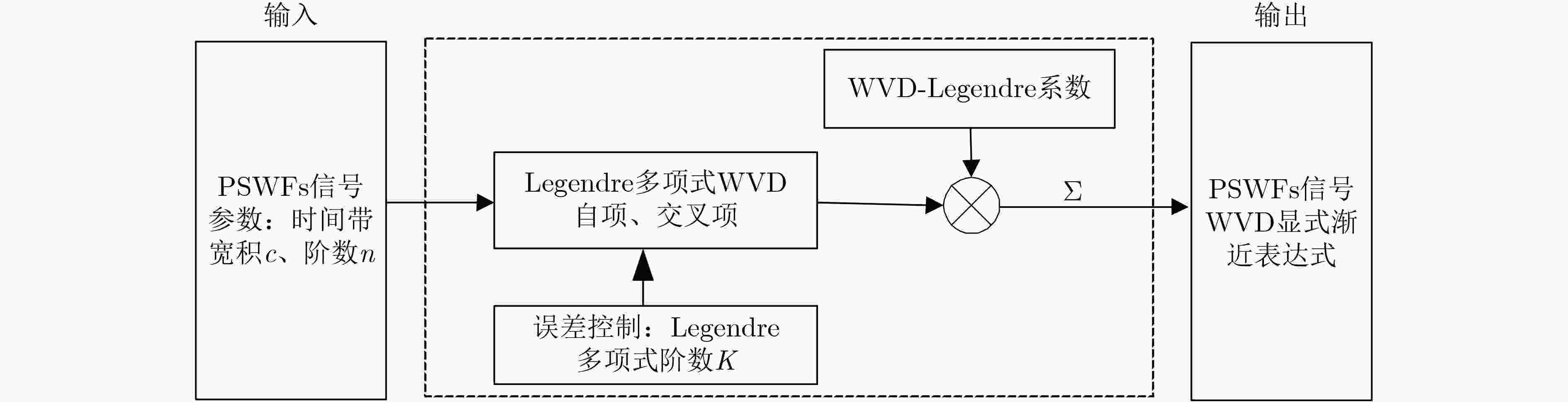
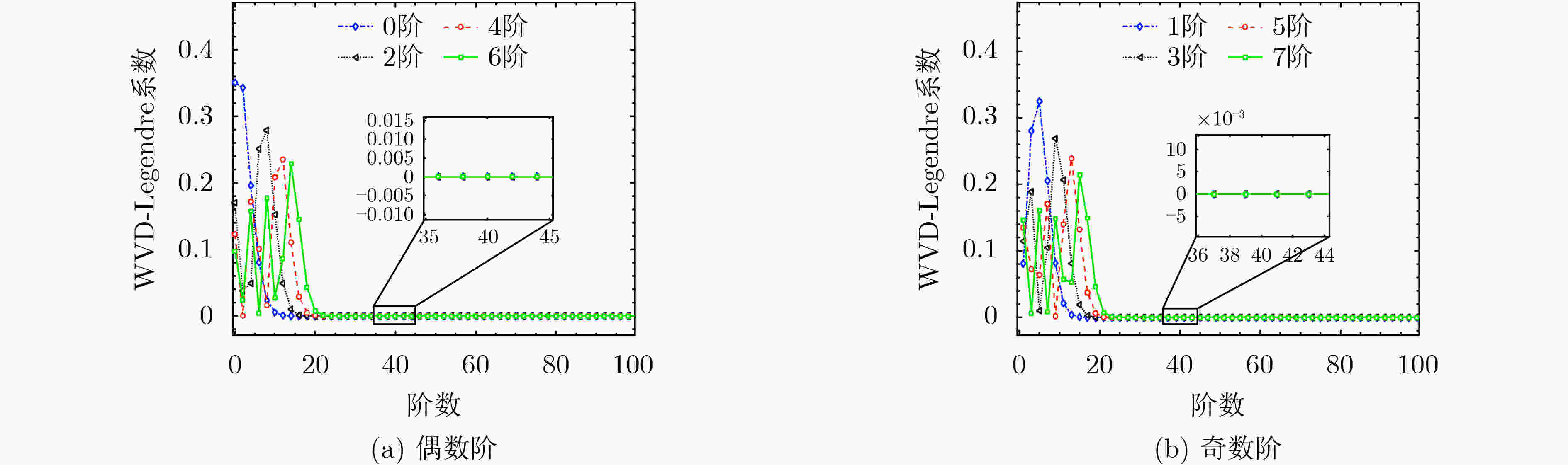
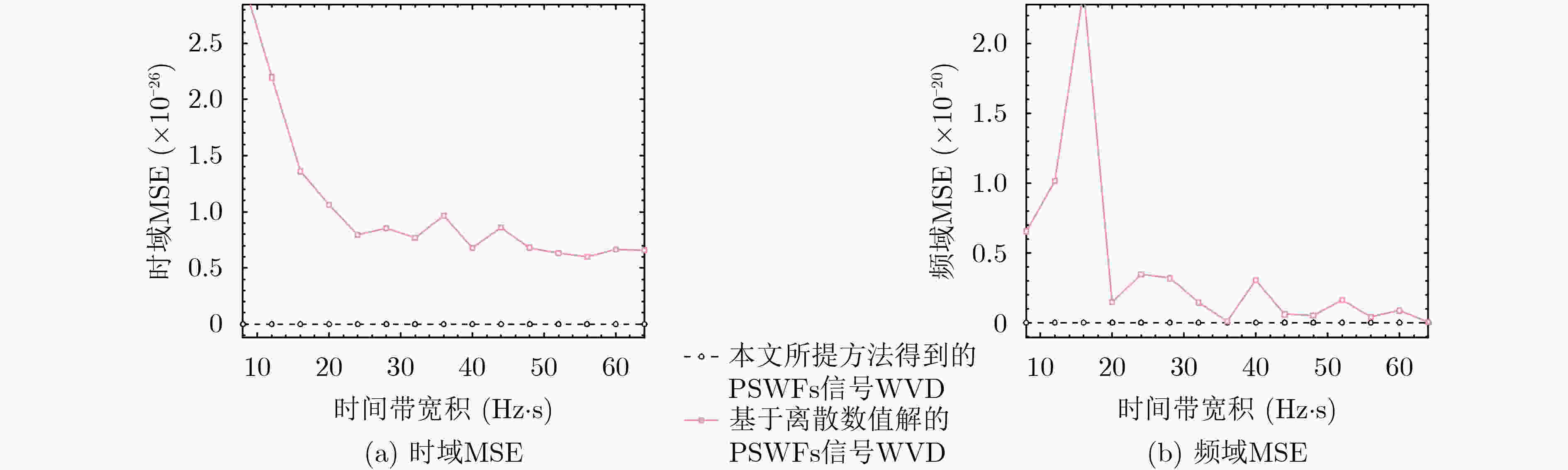
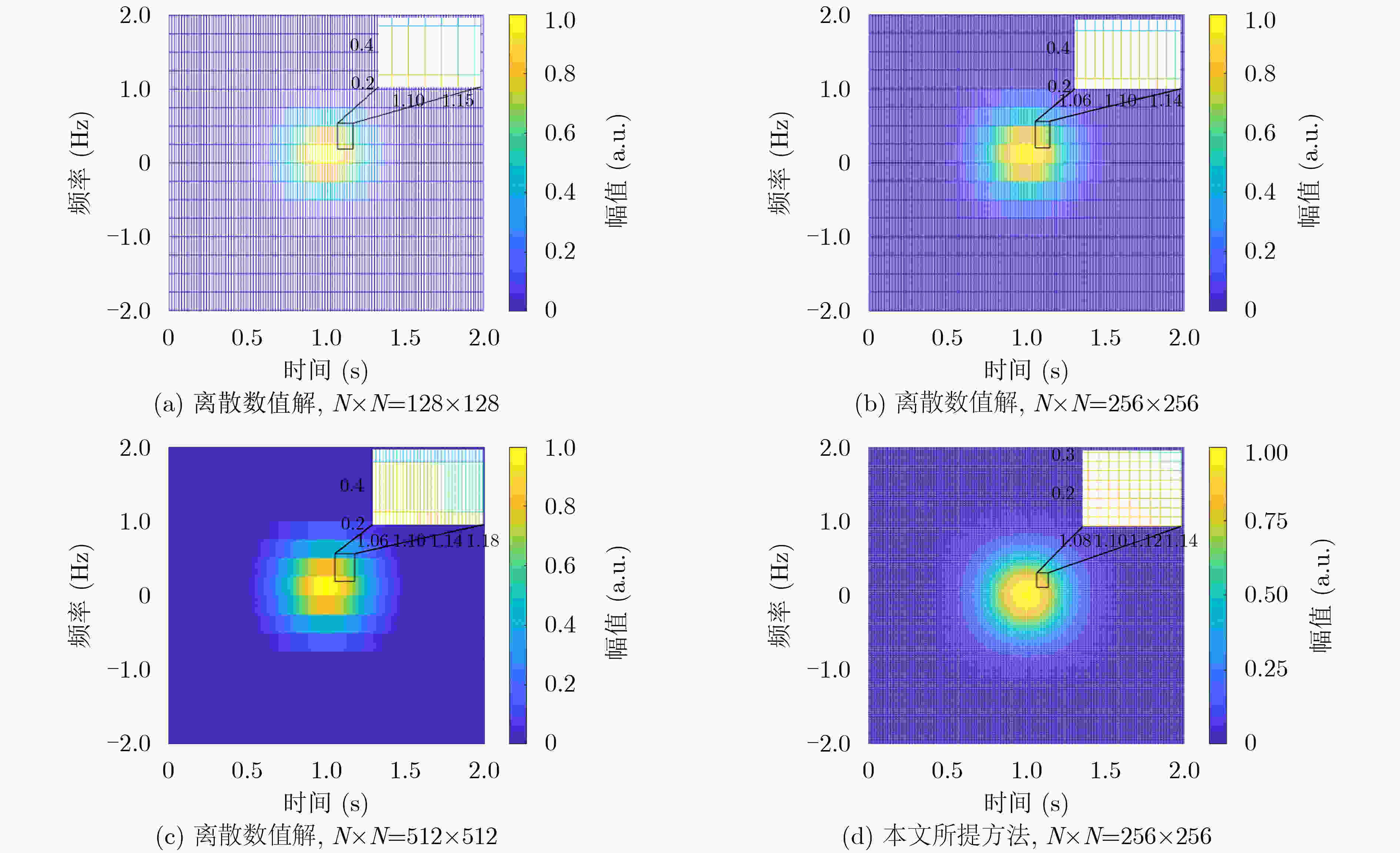
摘要: 针对现有的椭圆球面波函数(PSWFs)信号时频分析无显式表达式、数值仿真误差不可控、时频分布结果对称性缺失等问题，该文引入Legendre多项式以及Wigner-Ville分布(WVD)，提出一种PSWFs信号WVD显式渐近求解方法。该方法根据误差要求，生成所需阶数的Legendre多项式WVD自项、交叉项，进而与对应的WVD-Legendre系数相乘后线性叠加，获取PSWFs信号WVD显式渐近表达式。理论及数值仿真结果表明，所提方法能够产生满足误差要求的PSWFs信号WVD显式渐近表达式，且能够有效保持信号原有的时域、频域对称性。此外，在相同采样点数情况下，相对于基于数值解的PSWFs信号WVD，所提方法获得的PSWFs信号WVD频域分辨率更高。
- 椭圆球面波信号 /
- 时频分析 /
- Wigner-Ville分布 /
- 显式渐近
Abstract: Considering the problems of the existing time-frequency analysis of Prolate Spheroidal Wave Functions (PSWFs) signals without explicit expressions, uncontrollable numerical simulation errors, and lack of symmetry in the time-frequency distribution results, Legendre polynomials and Wigner- Ville Distribution (WVD) are introduced in this paper, and an explicit and progressive solution method for PSWFs signal WVD is proposed. According to the error requirements, this method generates the Legendre polynomial WVD self-terms and cross-terms of the required order, and then multiplies them with the corresponding WVD-Legendre coefficients and superimposes linearly them to obtain the explicit and progressive expression of the PSWFs signal WVD. Theoretical and numerical simulation results show that the proposed method can produce an explicit and progressive expression of the PSWFs signal WVD that meets the error requirements, and can effectively maintain the original time-domain and frequency-domain symmetry of the signal. In addition, in the case of the same number of sampling points, compared with the PSWFs signal WVD based on the numerical solution, the PSWFs signal WVD obtained by the proposed method has a higher frequency domain resolution.
- Prolate Spheroidal Wave Functions (PSWFs) /
- Time-frequency analysis /
- Wigner-Ville Distribution (WVD) /
- Explicitly progressive

HTML全文

图 1 PSWFs信号WVD显式渐近求解方法原理框图

下载: 全尺寸图片幻灯片

图 2 PSWFs信号对应的WVD-Legendre系数

下载: 全尺寸图片幻灯片

图 3 PSWFs信号MSE

下载: 全尺寸图片幻灯片

图 4 0阶PSWFs信号WVD

下载: 全尺寸图片幻灯片

表 1 PSWFs信号仿真参数设置

参数符号数值

时间带宽积(rad·s) c 4π: 4π: 64π
符号周期(s) T 2
阶数 n 0～7
采样点数 N 128, 256, 512

下载: 导出CSV

参考文献(21)

[1]	SLEPIAN D and POLLAK H O. Prolate spheroidal wave functions, Fourier analysis and uncertainty-I[J]. The Bell System Technical Journal, 1961, 40(1): 43–46. doi: 10.1002/j.1538-7305.1961.tb03976.x
[2]	WANG Hongxing, LU Faping, LIU Chuanhui, et al. Frequency domain multi-carrier modulation based on prolate spheroidal wave functions[J]. IEEE Access, 2020, 8: 99665–99680. doi: 10.1109/ACCESS.2020.2997679
[3]	陆发平, 王红星, 刘传辉, 等. 椭圆球面函数频域调制解调方法[J]. 电子与信息学报, 2020, 42(8): 1888–1895. doi: 10.11999/JEIT190642 LU Faping, WANG Hongxing, LIU Chuanhui, et al. PSWFs frequency domain modulation and demodulation method[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1888–1895. doi: 10.11999/JEIT190642
[4]	TAKAMI T, NIELSEN U D, and JENSEN J J. Estimation of autocorrelation function and spectrum density of wave-induced responses using prolate spheroidal wave functions[J]. Journal of Marine Science and Technology, 2021, 26(3): 772–791. doi: 10.1007/S00773-020-00768-9
[5]	NAZARI S and FAEZ K. Spiking pattern recognition using informative signal of image and unsupervised biologically plausible learning[J]. Neurocomputing, 2019, 330: 196–211. doi: 10.1016/j.neucom.2018.10.066
[6]	KARNIK S, ROMBERG J, and DAVENPORT M A. Improved bounds for the eigenvalues of prolate spheroidal wave functions and discrete prolate spheroidal sequences[J]. Applied and Computational Harmonic Analysis, 2021, 55: 97–128. doi: 10.1016/J.ACHA.2021.04.002
[7]	王红星, 陆发平, 刘传辉, 等. 基于信号分组优化的椭圆球面波多载波调制解调方法[J]. 中国科学:信息科学, 2021, 51(7): 1168–1182. doi: 10.1360/SSI-2020-0007 WANG Hongxing, LU Faping, LIU Chuanhui, et al. Multi-carrier modulation scheme based on prolate spheroidal wave functions with signal grouping optimization[J]. Scientia Sinica Informationis, 2021, 51(7): 1168–1182. doi: 10.1360/SSI-2020-0007
[8]	陆发平, 王红星, 刘传辉, 等. 基于功率复用的椭圆球面波函数非正交调制方法[J]. 航空学报, 2019, 40(9): 323102. doi: 10.7527/S1000-6893.2019.23102 LU Faping, WANG Hongxing, LIU Chuanhui, et al. Power domain non-orthogonal pulse modulation based on prolate spheroidal wave function[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(9): 323102. doi: 10.7527/S1000-6893.2019.23102
[9]	王红星, 陆发平, 刘传辉, 等. 椭圆球面波信号间交叉项时频分布特性研究[J]. 电子与信息学报, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877 WANG Hongxing, LU Faping, LIU Chuanhui, et al. Study on time-frequency characteristics of cross-terms between prolate spheroidal wave function signal[J]. Journal of Electronics &Information Technology, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877
[10]	缪幸吉, 王红星, 刘传辉, 等. 椭圆球面波函数信号时频分布特性研究[J]. 现代电子技术, 2020, 43(19): 14–18,22. doi: 10.16652/j.issn.1004-373x.2020.19.004 MIAO Xingji, WANG Hongxing, LIU Chuanhui, et al. Research of time-frequency distribution characteristics of prolate spherical wave function signal[J]. Modern Electronics Technique, 2020, 43(19): 14–18,22. doi: 10.16652/j.issn.1004-373x.2020.19.004
[11]	黄隽逸, 王红星, 陆发平, 等. PSWFs信号时频域能量分布特性与正交性研究[J]. 无线电通信技术, 2020, 46(6): 682–688. doi: 10.3969/j.issn.1003-3114.2020.06.009 HUANG Junyi, WANG Hongxing, LU Faping, et al. Study on energy distribution characteristics and orthogonality of PSWFs signal in time-frequency domain[J]. Radio Communications Technology, 2020, 46(6): 682–688. doi: 10.3969/j.issn.1003-3114.2020.06.009
[12]	吴国宁, 齐晶晶, 周亚同. 时频分析方法: 研究与展望[J]. 图像与信号处理, 2018, 7(1): 24–35. doi: 10.12677/jisp.2018.71003 WU Guoning, QI Jingjing, and ZHOU Yatong. Time-frequency analysis method: Research and prospect[J]. Journal of Image and Signal Processing, 2018, 7(1): 24–35. doi: 10.12677/jisp.2018.71003
[13]	王德真, 王众毅, 王晓东. 基于Wigner-Ville时频分析的行波信号检测方法[J]. 电测与仪表, 2020, 57(3): 128–133. doi: 10.19753/j.issn1001-1390.2020.03.021 WANG Dezhen, WANG Zhongyi, and WANG Xiaodong. The detection method for traveling wave based on Wigner-Ville time-frequency analysis[J]. Electrical Measurement &Instrumentation, 2020, 57(3): 128–133. doi: 10.19753/j.issn1001-1390.2020.03.021
[14]	陈彦江, 王凯, 马裕超, 等. 基于Wigner-Ville分布交叉项的独塔自锚式悬索桥损伤识别试验研究[J]. 振动与冲击, 2016, 35(6): 161–168. doi: 10.13465/j.cnki.jvs.2016.06.030 CHEN Yanjiang, WANG Kai, MA Yuchao, et al. Experimental study of single-tower self-anchored suspension bridge damage identification based on cross terms of Wigner-Ville distribution[J]. Journal of Vibration and Shock, 2016, 35(6): 161–168. doi: 10.13465/j.cnki.jvs.2016.06.030
[15]	王红星, 陆发平, 刘传辉, 等. 严格奇偶对称的椭圆球面波函数信号构建与低复杂度检测方法[J]. 中国科学:信息科学, 2020, 50(5): 766–776. doi: 10.1360/SSI-2019-0121 WANG Hongxing, LU Faping, LIU Chuanhui, et al. Strict parity symmetric prolate spheroidal wave functions signal construction and low complexity detection method[J]. Scientia Sinica Informationis, 2020, 50(5): 766–776. doi: 10.1360/SSI-2019-0121
[16]	HODGE D B. Eigenvalues and eigenfunctions of the spheroidal wave equation[J]. Journal of Mathematical Physics, 1970, 11(8): 2308–2312. doi: 10.1063/1.1665398
[17]	胡广书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2004: 72–75. HU Guangshu. Modern Signal Processing Course[M]. Beijing: Tsinghua University Press, 2004: 72–75.
[18]	FLAMMER C. Spheroidal Wave Functions[M]. Mineola: Dover Publications, 2005: 16–20.
[19]	XIAO H, ROKHLIN V, and YARVIN N. Prolate spheroidal wavefunctions, quadrature and interpolation[J]. Inverse Problems, 2001, 17(4): 805–833. doi: 10.1088/0266-5611/17/4/315
[20]	FLANDRIN P. A time-frequency formulation of optimum detection[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(9): 1377–1384. doi: 10.1109/29.90365
[21]	赛雷, 王红星, 陆发平, 等. 一种大时间带宽积PSWF的显式渐近表达式[J]. 中国科学:信息科学, 2020, 50(10): 1574–1587. doi: 10.1360/SSI-2019-0092 SAI Lei, WANG Hongxing, LU Faping, et al. An explicit asymptotic expression of large time-bandwidth product PSWF[J]. Scientia Sinica Informationis, 2020, 50(10): 1574–1587. doi: 10.1360/SSI-2019-0092