Correlation and Sparse Representation Based Channel Selection of Motor Imagery Electroencephalogram
-
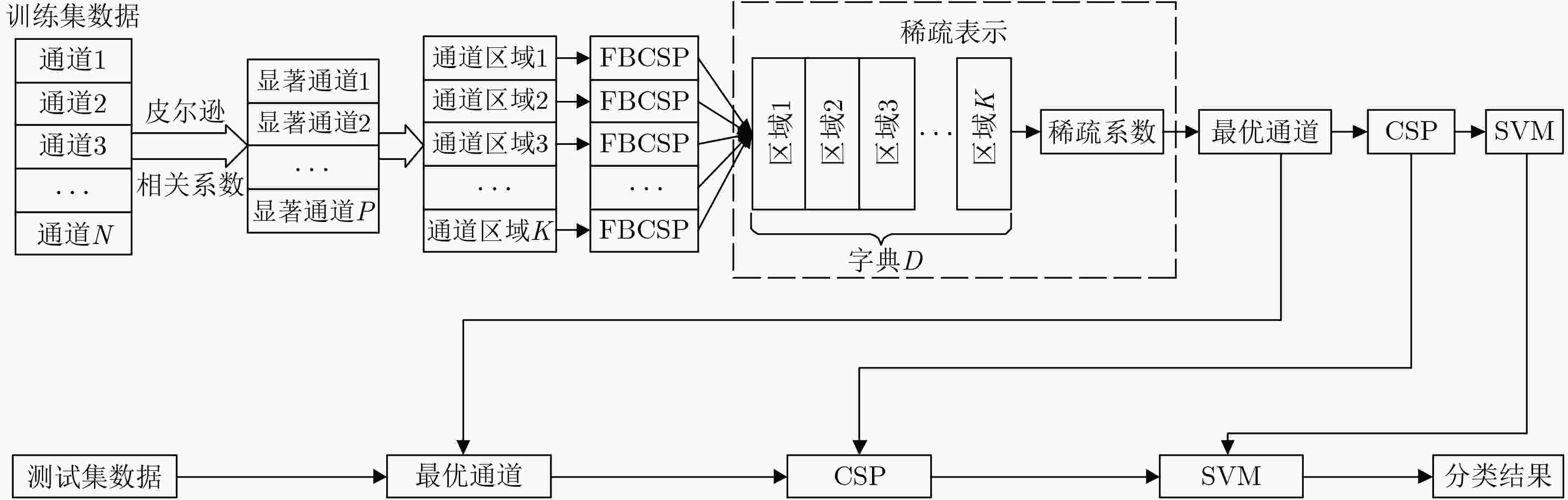
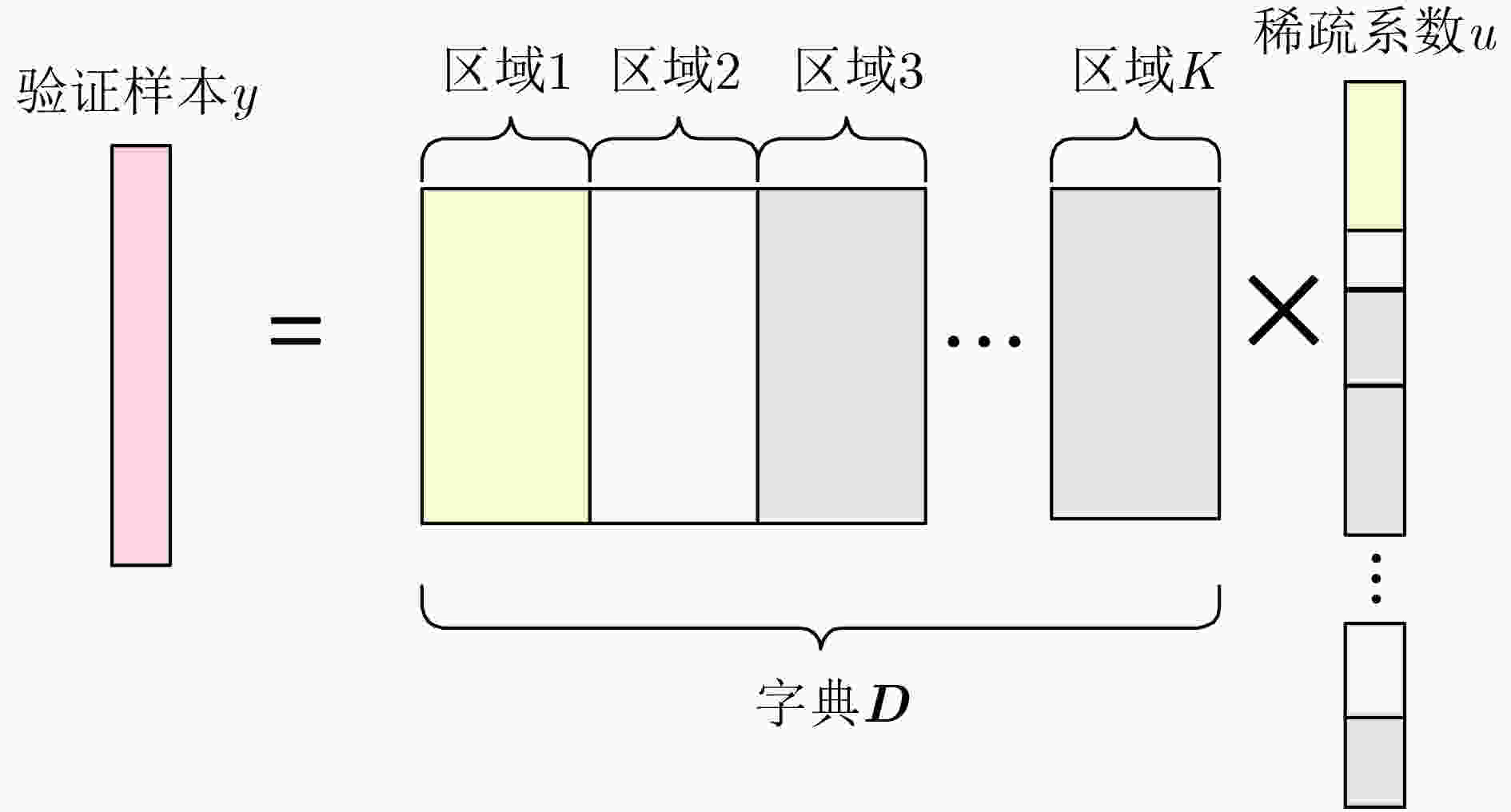
摘要: 在基于运动想象(MI)的脑机接口(BCI)中,通常采用较多通道的脑电信号(EEG)来提高分类精度,但其中会有包含与MI任务无关或冗余信息的通道,从而影响BCI的性能提升。该文针对运动想象脑电分类中的通道选择问题,提出一种采用相关性和稀疏表示对通道进行选择的方法(CSR-CS)。首先计算训练样本每个通道的皮尔逊相关系数来选择显著通道,然后提取显著通道所在区域的滤波器组共空间模式特征拼接成字典,利用由字典所得到的非零稀疏系数的个数表征每个区域的分类能力,选出显著区域所包含的显著通道作为最优通道,最后采用共空间模式和支持向量机分别进行特征提取与分类。在对BCI第3次竞赛数据集IVa和BCI第4次竞赛数据集I两个二分类MI任务的分类实验中,平均分类精度达到了88.61%和83.9%,表明所提通道选择方法的有效性和鲁棒性。Abstract: In Motor Imagery (MI) based Brain Computer Interface (BCI), more channels of ElectroEncephaloGram (EEG) signal are usually adopted to improve the classification accuracy. But there will be channels containing irrelevant or redundant information about MI tasks, which degenerate the performance improvement of BCI. A Channel Selection method based on Correlation and Sparse Representation (CSR-CS) is proposed for EEG classification. Firstly, the Pearson correlation coefficient of each channel of the training sample is calculated to select the significant channels. Then the filter bank common spatial pattern features of the region where the significant channels are located are extracted and spliced into a dictionary. The number of non-zero sparse coefficients obtained from the dictionary is used to characterize the classification ability of each region, and the significant channels contained in the significant regions are selected as the optimal channels. Finally, the common spatial pattern and support vector machine are employed for feature extraction and classification respectively. In the classification experiments of two categories of MI task with BCI competition III dataset IVa and BCI competition IV dataset I, the average classification accuracy reaches 88.61% and 83.9%, which indicates the effectiveness and robustness of the proposed channel selection method.
-
表 1 数据集Ⅰ、数据集Ⅱ分类精度比较
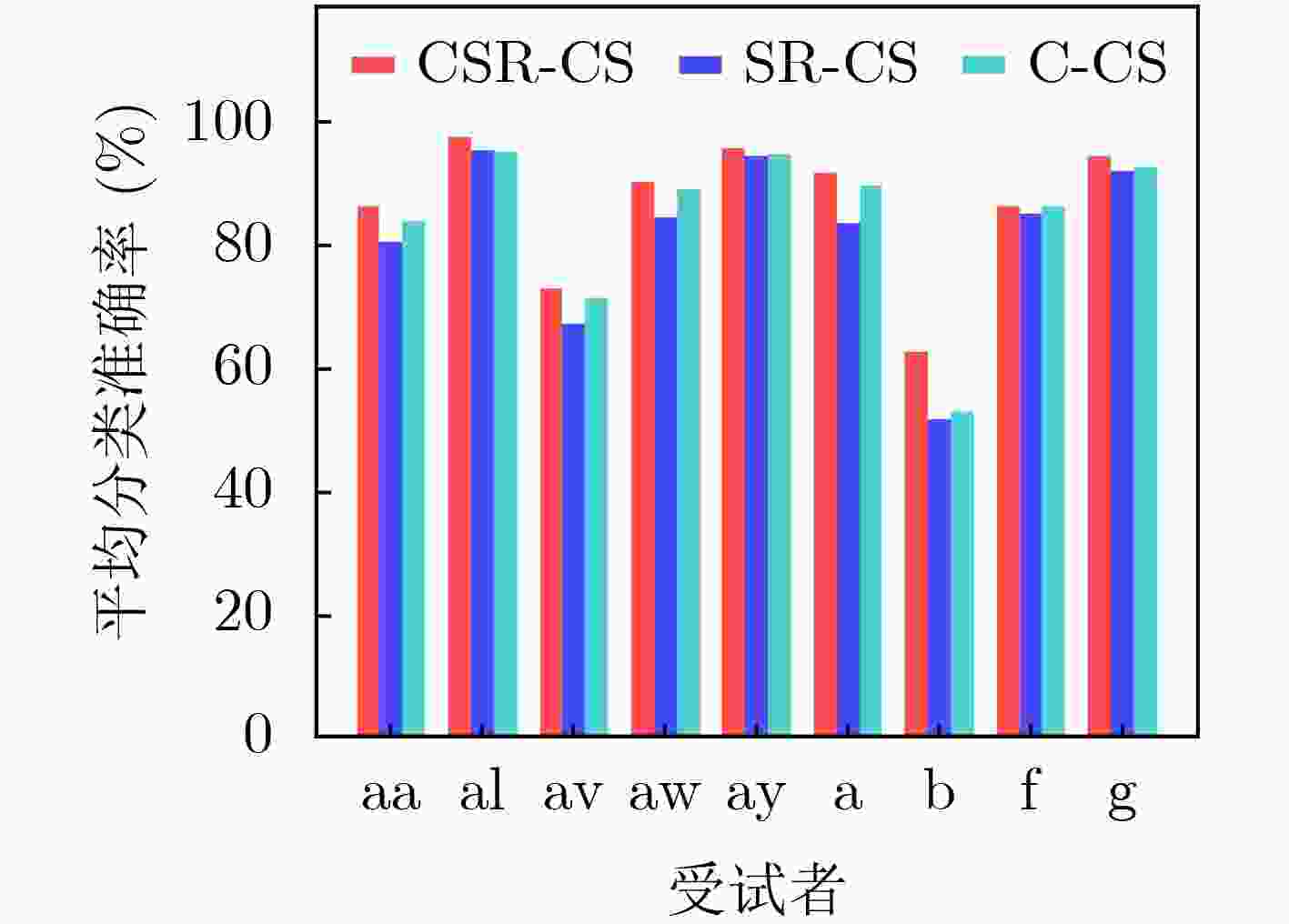
受试者 方法 CCS-RCSP CSP-R-MF FCCR CSR-CS aa 82.50 81.43 78.57 86.31 al 96.80 92.41 98.21 97.74 av 71.10 70.00 72.45 72.83 aw 92.90 83.57 87.05 90.48 ay 93.90 85.00 93.25 95.71 均值 87.44 82.48 85.91 88.61 a 85.50 81.50 83.50 92.00 b 67.00 63.00 72.50 62.50 f 79.50 79.00 81.00 86.30 g 94.50 87.50 83.50 94.70 均值 81.60 77.80 80.10 83.90 p-value 0.21 <0.01 0.16 – 表 2 通道选择与否对分类准确率的影响
方法 数据集Ⅰ 数据集Ⅱ aa al av aw ay 均值 a b f g 均值 p-value AC-CSP 76.19 95.12 66.02 83.69 94.88 83.18 82.50 52.50 85.10 92.30 78.10 <0.01 CSR-CS 86.31 97.74 72.83 90.48 95.71 88.61 92.00 62.50 86.30 94.70 83.90 – -
[1] BIRBAUMER N. Brain–computer-interface research: Coming of age[J]. Clinical Neurophysiology, 2006, 117(3): 479–483. doi: 10.1016/j.clinph.2005.11.002 [2] BLANKERTZ B, DORNHEGE G, KRAULEDAT M, et al. The non-invasive Berlin Brain–Computer Interface: Fast acquisition of effective performance in untrained subjects[J]. NeuroImage, 2007, 37(2): 539–550. doi: 10.1016/j.neuroimage.2007.01.051 [3] ALLISON B Z, KÜBLER A, and JIN Jing. 30+years of P300 brain-computer interfaces[J]. Psychophysiology, 2020, 57(7): e13569. doi: 10.1111/psyp.13569 [4] HSU C C, YEH C L, LEE W K, et al. Extraction of high-frequency SSVEP for BCI control using iterative filtering based empirical mode decomposition[J]. Biomedical Signal Processing and Control, 2020, 61: 102022. doi: 10.1016/j.bspc.2020.102022 [5] ANG K K and GUAN Cuntai. EEG-based strategies to detect motor imagery for control and rehabilitation[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2017, 25(4): 392–401. doi: 10.1109/TNSRE.2016.2646763 [6] RONG Yuying, WU Xiaojun, and ZHANG Yumei. Classification of motor imagery electroencephalography signals using continuous small convolutional neural network[J]. International Journal of Imaging Systems and Technology, 2020, 30(3): 653–659. doi: 10.1002/ima.22405 [7] PARK Y and CHUNG W. A novel EEG correlation coefficient feature extraction approach based on demixing EEG channel pairs for cognitive task classification[J]. IEEE Access, 2020, 8: 87422–87433. doi: 10.1109/access.2020.2993318 [8] BLANKERTZ B, LOSCH F, KRAULEDAT M, et al. The Berlin brain-computer interface: Accurate performance from first-session in BCI-naive subjects[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(10): 2452–2462. doi: 10.1109/TBME.2008.923152 [9] LIU Ye, ZHANG Hao, CHEN Min, et al. A boosting-based spatial-spectral model for stroke patients’ EEG analysis in rehabilitation training[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2016, 24(1): 169–179. doi: 10.1109/TNSRE.2015.2466079 [10] ASENSIO-CUBERO J, GAN J Q, and PALANIAPPAN R. Multiresolution analysis over simple graphs for brain computer interfaces[J]. Journal of Neural Engineering, 2013, 10(4): 046014. doi: 10.1088/1741-2560/10/4/046014 [11] FENG Jiankui, JIN Jing, DALY I, et al. An optimized channel selection method based on multifrequency CSP-Rank for motor imagery-based BCI system[J]. Computational Intelligence and Neuroscience, 2019, 2019: 8068357. doi: 10.1155/2019/8068357 [12] JIN Jing, MIAO Yangyang, DALY I, et al. Correlation-based channel selection and regularized feature optimization for MI-based BCI[J]. Neural Networks, 2019, 118: 262–270. doi: 10.1016/j.neunet.2019.07.008 [13] VARSEHI H and FIROOZABADI S M P. An EEG channel selection method for motor imagery based brain–computer interface and neurofeedback using Granger causality[J]. Neural Networks, 2021, 133: 193–206. doi: 10.1016/j.neunet.2020.11.002 [14] HAN Jiuqi, ZHAO Yuwei, SUN Hongji, et al. A fast, open EEG classification framework based on feature compression and channel ranking[J]. Frontiers in Neuroscience, 2018, 12: 217. doi: 10.3389/fnins.2018.00217 [15] CONA F, ZAVAGLIA M, ASTOLFI L, et al. Changes in EEG power spectral density and cortical connectivity in healthy and tetraplegic patients during a motor imagery task[J]. Computational Intelligence and Neuroscience, 2009, 2009: 279515. doi: 10.1155/2009/279515 [16] HAMEDI M, SALLEH S, and NOOR A M. Electroencephalographic motor imagery brain connectivity analysis for BCI: A review[J]. Neural Computation, 2016, 28(6): 999–1041. doi: 10.1162/NECO_a_00838 [17] ANG K K, CHIN Z Y, ZHANG Haihong, et al. Filter bank common spatial pattern (FBCSP) in brain-computer interface[C]. 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 2008: 2390–2397. [18] SHIN Y, LEE S, AHN M, et al. Noise robustness analysis of sparse representation based classification method for non-stationary EEG signal classification[J]. Biomedical Signal Processing and Control, 2015, 21: 8–18. doi: 10.1016/j.bspc.2015.05.007 [19] LI Yuanqing, NAMBURI P, YU Zhuliang, et al. Voxel selection in fMRI data analysis based on sparse representation[J]. IEEE Transactions on Biomedical Engineering, 2009, 56(10): 2439–2451. doi: 10.1109/TBME.2009.2025866 [20] XU Chunyao, SUN Chao, JIANG Guoqian, et al. Two-Level multi-domain feature extraction on sparse representation for motor imagery classification[J]. Biomedical Signal Processing and Control, 2020, 62: 102160. doi: 10.1016/j.bspc.2020.102160 [21] SREEJA S R, HIMANSHU, and SAMANTA D. Distance-based weighted sparse representation to classify motor imagery EEG signals for BCI applications[J]. Multimedia Tools and Applications, 2020, 79(19): 13775–13793. doi: 10.1007/s11042-019-08602-0 [22] JIAO Yong, ZHANG Yu, CHEN Xun, et al. Sparse group representation model for motor imagery EEG classification[J]. IEEE Journal of Biomedical and Health Informatics, 2019, 23(2): 631–641. doi: 10.1109/JBHI.2018.2832538 -





 下载:
下载:


 下载:
下载:
