A Improved Logistic Chaotic Map and Its Application to Image Encryption and Hiding
-
摘要: 鉴于原Logistic映射的映射范围有限、混沌参数范围小、分布不均匀等缺陷,该文提出一个新的改进型Logistic混沌映射。该映射有
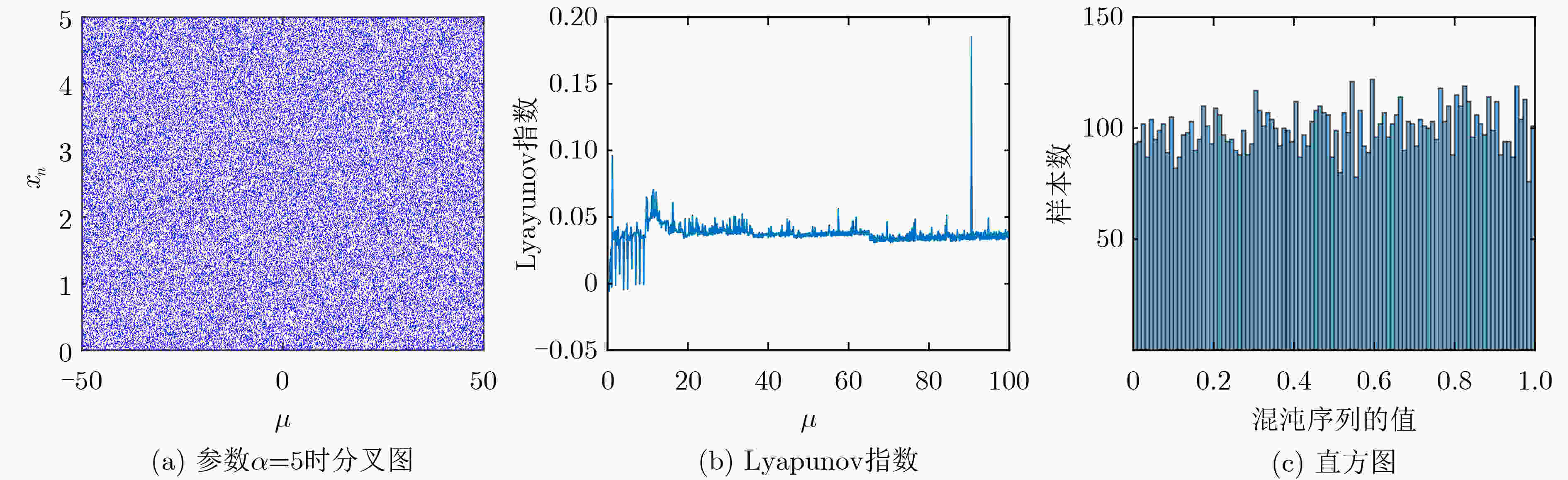
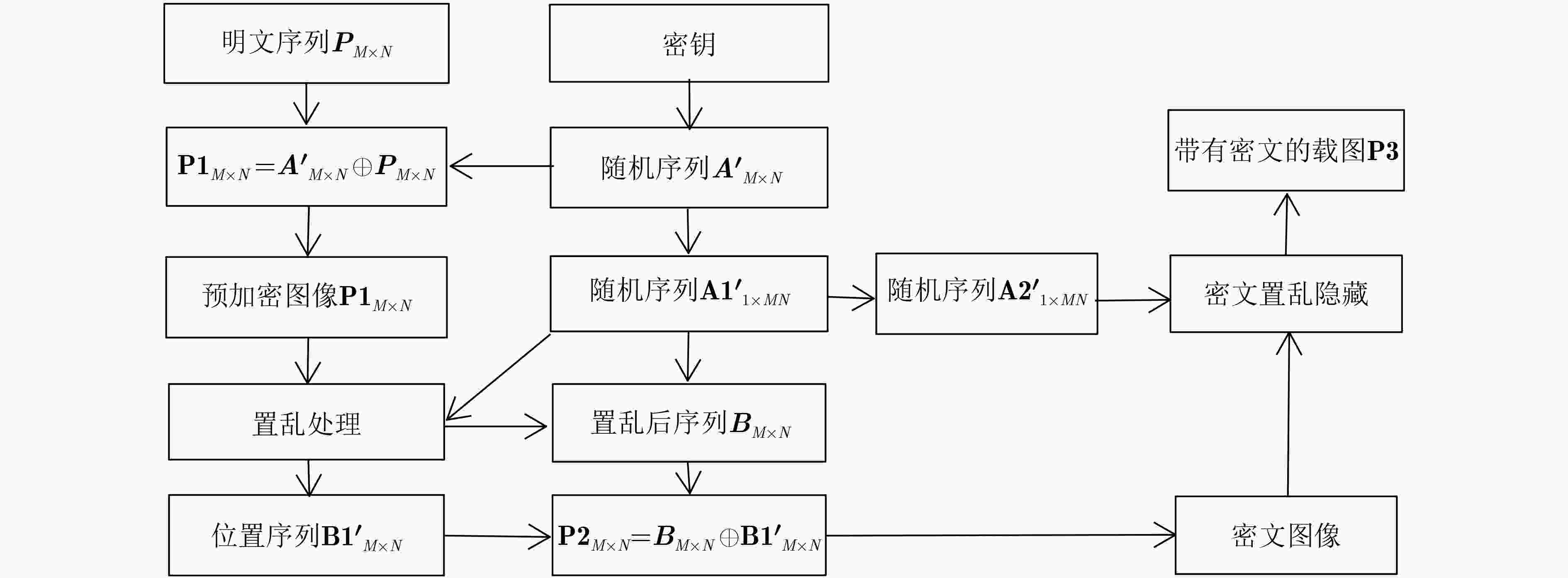
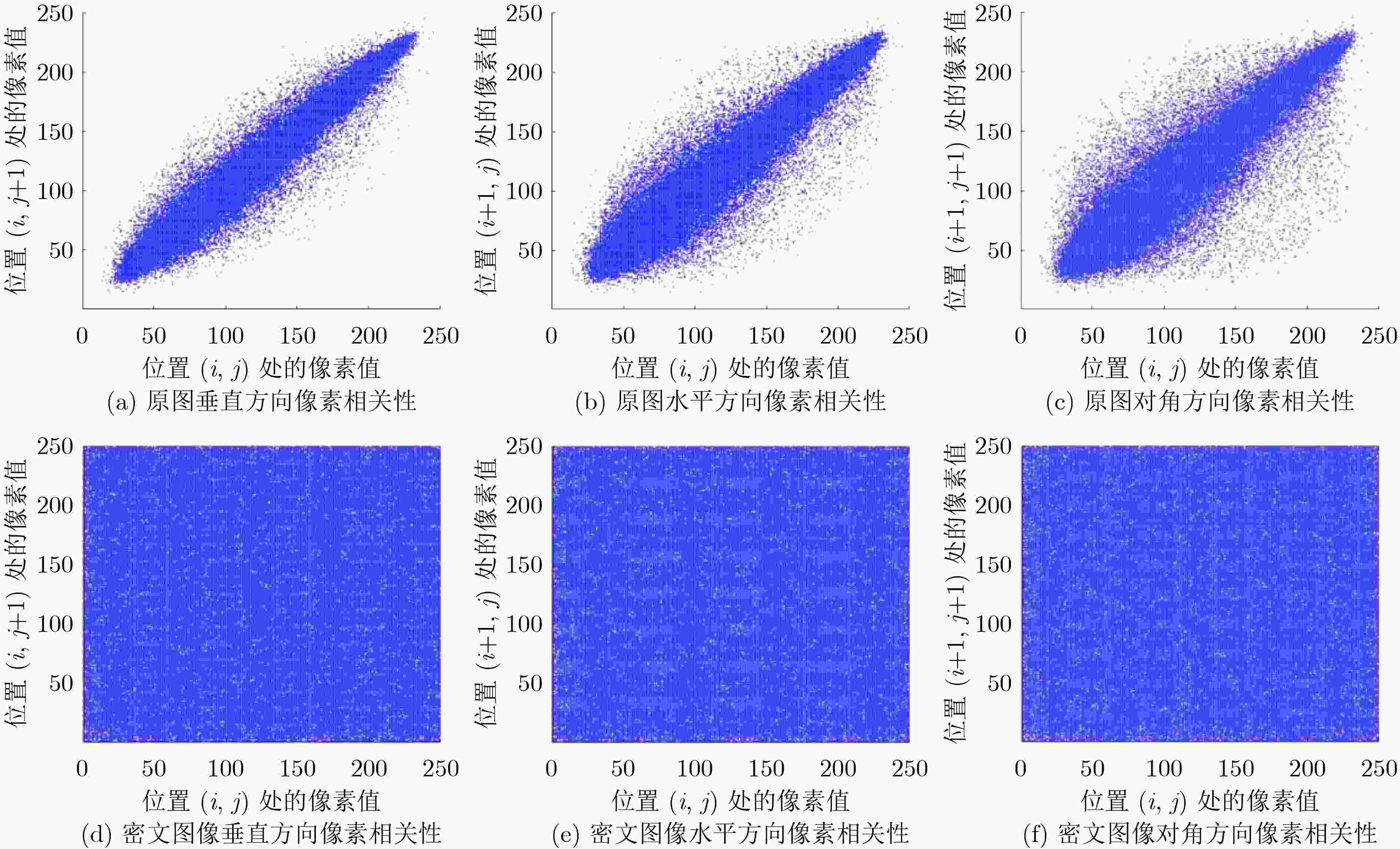
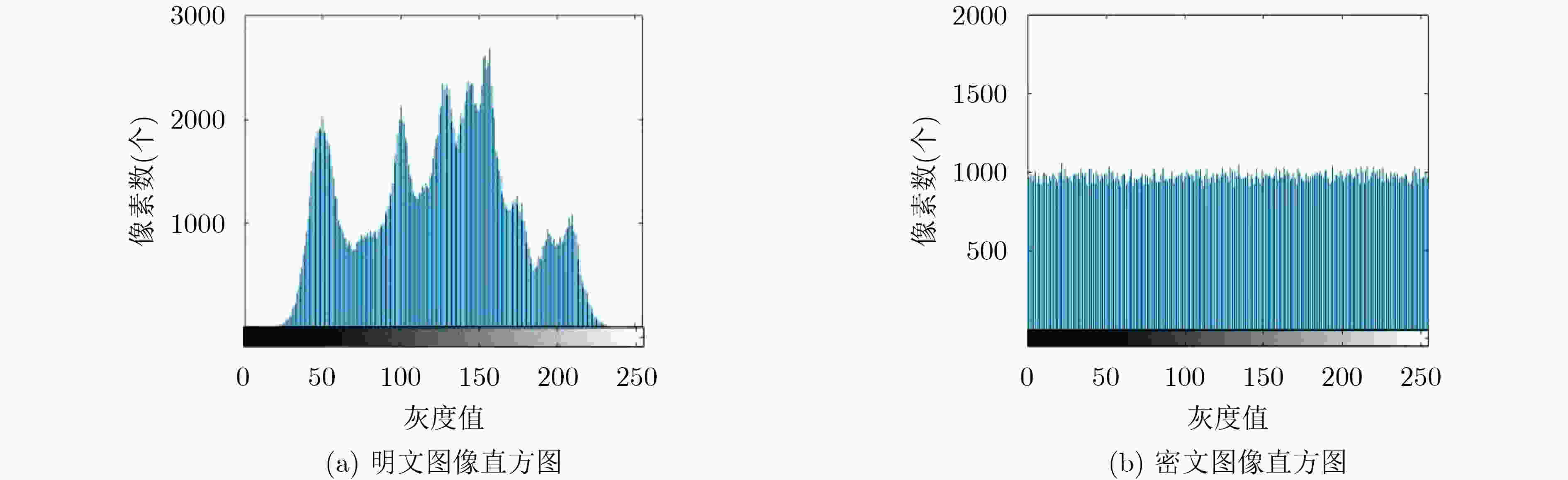
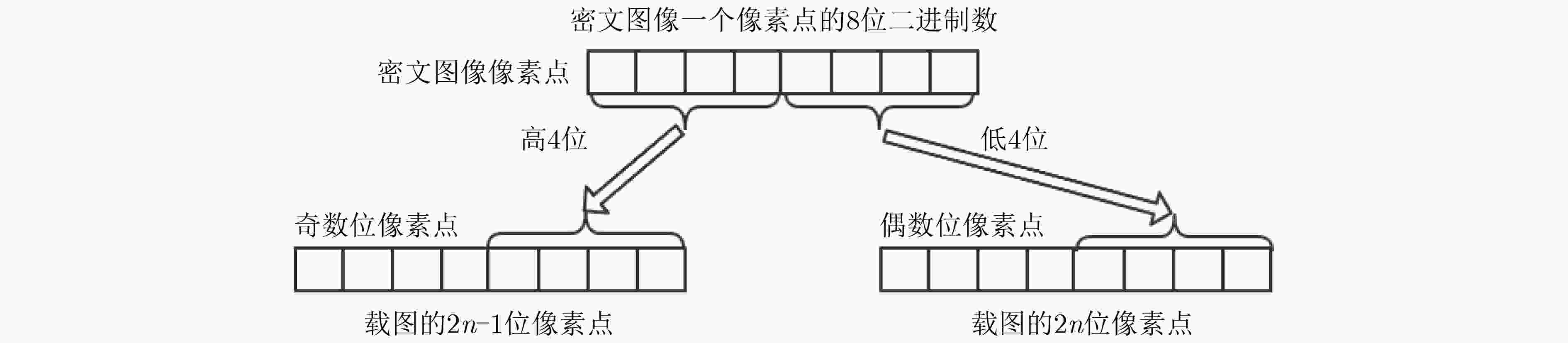
$ \mu $ 和$ \alpha $ 两个参数,$ {x_{n - 1}} $ 和$ {x_n} $ 两个初值,参数和初值选取范围可扩展到任意实数,其混沌映射均为满映射,且映射范围可任意调控。将该映射应用到图像加密,其算法采用像素值异或(XOR)加密、像素位置置乱处理。之后再把密文数据隐藏在与密文无关的载图之中。对密文图像做了一系列的分析,包括图像的相邻像素点相关性,直方图分析和密钥敏感性测试。分析结果表明,所提加密算法具有很好的安全性和加密效果。-
关键词:
- Logistic混沌映射 /
- 图像加密 /
- 图像隐藏
Abstract: In view of the limited mapping range of the original Logistic map, the small range of chaotic parameters, and the uneven distribution, a new improved Logistic chaotic map is proposed. The mapping has two parameters$ \mu $ and$ \alpha $ , and two initial values of$ {x_{n - 1}} $ and$ {x_n} $ . The parameter and initial value selection range can be extended to any real number. The chaotic mapping is full mapping, and the mapping range can be adjusted arbitrarily. This mapping is applied to image encryption, and the algorithm uses pixel value Exclusive OR(XOR) encryption and pixel position is scrambled . Afterwards, the ciphertext data is hidden in the image that has nothing to do with the ciphertext. A series of analysis is done on the ciphertext image, including the correlation between adjacent pixels of the image, histogram analysis and key sensitivity test. The analysis result shows that the proposed encryption algorithm has good security and encryption effect.-
Key words:
- Logistic chaotic map /
- Image encryption /
- Image hiding
-
表 1 Logistic映射与改进的Logistic映射比较
映射范围 初值取值范围 参数µ取值范围 原Logistic映射 [0,1] [0,1] (0,4] 改进的Logistic映射 任意实数 任意实数 任意实数 表 2 明文/密文图像在3个方向上的相关系数
垂直方向 水平方向 对角方向 明文图像 0.9780 0.9685 0.9380 密文图像 0.0029 –0.0342 –0.0021 表 3 密钥敏感性分析(%)
NPCR UACI 只改变$ {x_{n - 1}} $ 99.5468 33.5983 只改变$ {x_n} $ 99.5692 33.6474 只改变$ \mu $ 99.5796 33.6091 表 4 明文敏感性分析(%)
NPCR UACI 像素点1 99.5724 33.6345 像素点2 99.5716 33.6354 像素点3 99.5728 33.6357 平均值 99.5723 33.6352 -
[1] 郝晋, 王伟, 李庆宇, 等. 基于混沌序列与DNA突变原理的彩色图像加密方案[J]. 大连工业大学学报, 2021, 40(3): 214–221. doi: 10.19670/j.cnki.dlgydxxb.2021.0703HAO Jin, WANG Wei, LI Qingyu, et al. Color image encryption scheme based on chaotic sequences and DNA mutation principle[J]. Journal of Dalian Polytechnic University, 2021, 40(3): 214–221. doi: 10.19670/j.cnki.dlgydxxb.2021.0703 [2] 范九伦, 张雪锋. 分段Logistic混沌映射及其性能分析[J]. 电子学报, 2009, 37(4): 720–725. doi: 10.3321/j.issn:0372-2112.2009.04.009FAN Jiulun and ZHANG Xuefeng. Piecewise Logistic chaotic map and its performance analysis[J]. Acta Electronica Sinica, 2009, 37(4): 720–725. doi: 10.3321/j.issn:0372-2112.2009.04.009 [3] 陈志刚, 梁涤青, 邓小鸿, 等. Logistic混沌映射性能分析与改进[J]. 电子与信息学报, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039CHEN Zhigang, LIANG Diqing, DENG Xiaohong, et al. Performance analysis and improvement of Logistic chaotic mapping[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039 [4] HUA Zhongyun and ZHOU Yicong. Exponential chaotic model for generating robust chaos[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2021, 51(6): 3713–3724. doi: 10.1109/TSMC.2019.2932616 [5] HUA Zhongyun, JIN Fan, XU Binxuan, et al. 2D Logistic-sine-coupling map for image encryption[J]. Signal Processing, 2018, 149: 148–161. doi: 10.1016/j.sigpro.2018.03.010 [6] 曾祥秋, 叶瑞松. 基于改进Logistic映射的混沌图像加密算法[J]. 计算机工程, 2021, 47(11): 158–165,174. doi: 10.19678/j.issn.1000-3428.0059928ZENG Xiangqiu and YE Ruisong. Chaotic image encryption algorithm based on improved Logistic map[J]. Computer Engineering, 2021, 47(11): 158–165,174. doi: 10.19678/j.issn.1000-3428.0059928 [7] HUA Zhongyun, ZHOU Yicong, and HUANG Hejiao. Cosine-transform-based chaotic system for image encryption[J]. Information Sciences, 2019, 480: 403–419. doi: 10.1016/j.ins.2018.12.048 [8] 杨吉云, 吴昊. 基于混沌系统和动态DNA编码与运算的彩色图像加密算法[J]. 计算机工程, 2018, 44(2): 151–157. doi: 10.3969/j.issn.1000-3428.2018.02.027YANG Jiyun and WU Hao. Color image encryption algorithm based on chaotic system and dynamic DNA coding and operation[J]. Computer Engineering, 2018, 44(2): 151–157. doi: 10.3969/j.issn.1000-3428.2018.02.027 [9] LIU Zeyu and XIA Tiecheng. Novel two dimensional fractional-order discrete chaotic map and its application to image encryption[J]. Applied Computing and Informatics, 2018, 14(2): 177–185. doi: 10.1016/j.aci.2017.07.002 [10] SHANNON C E. Communication theory of secrecy systems[J]. The Bell System Technical Journal, 1949, 28(4): 656–715. doi: 10.1002/j.1538-7305.1949.tb00928.x [11] 章秀君, 吴志强, 方正. 一种基于四维超混沌系统的数字图像加密算法[J]. 计算机工程, 2013, 39(8): 169–172. doi: 10.3969/j.issn.1000-3428.2013.08.036ZHANG Xiujun, WU Zhiqiang, and FANG Zheng. A digital image encryption algorithm based on four-dimensional hyperchaotic system[J]. Computer Engineering, 2013, 39(8): 169–172. doi: 10.3969/j.issn.1000-3428.2013.08.036 [12] 庄志本, 刘静漪, 李军, 等. 一种基于五维超混沌系统的数字图像加密算法[J]. 湖北民族学院学报:自然科学版, 2019, 37(2): 195–200. doi: 10.13501/j.cnki.42-1569/n.2019.06.016ZHUANG Zhiben, LIU Jingyi, LI Jun, et al. A digital image encryption algorithm based on five-dimensional hyperchaotic system[J]. Journal of HuBei Minzu University:Natural Science Edition, 2019, 37(2): 195–200. doi: 10.13501/j.cnki.42-1569/n.2019.06.016 [13] 刘睿. 基于改进Logistic混沌映射的图像自适应加密算法[J]. 计算机与现代化, 2016(7): 13–17,23. doi: 10.3969/j.issn.1006-2475.2016.07.003LIU Rui. Self-adaptive image encryption algorithm based on improved Logistic chaotic map[J]. Computer and Modernization, 2016(7): 13–17,23. doi: 10.3969/j.issn.1006-2475.2016.07.003 [14] 李楠, 任清华, 苏玉泽. 基于改进型Logistic混沌序列的SPC-TDCS多址接入研究[J]. 空军工程大学学报:自然科学版, 2016, 17(3): 45–50. doi: 10.3969/j.issn.1009-3516.2016.03.009LI Nan, REN Qinghua, and SU Yuze. Research on multiple accesses of SPC TDCS based on modified Logistic chaotic sequence[J]. Journal of Air Force Engineering University:Natural Science Edition, 2016, 17(3): 45–50. doi: 10.3969/j.issn.1009-3516.2016.03.009 [15] XU Lu, LI Zhi, LI Jian, et al. A novel bit-level image encryption algorithm based on chaotic maps[J]. Optics and Lasers in Engineering, 2012, 78: 17–25. doi: 10.1016/j.optlaseng.2015.09.007 [16] ZHOU Yicong, CAO Weijia, and CHEN C L P. Image encryption using binary bitplane[J]. Signal Processing, 2014, 100: 197–207. doi: 10.1016/j.sigpro.2014.01.020 [17] 李付鹏, 刘敬彪, 王光义, 等. 基于混沌集的图像加密算法[J]. 电子与信息学报, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344LI Fupeng, LIU Jingbiao, WANG Guangyi, et al. An image encryption algorithm based on chaos set[J]. Journal of Electronics &Information Technology, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344 [18] CHAN C K and CHENG L M. Hiding data in images by simple LSB substitution[J]. Pattern Recognition, 2004, 37(3): 469–474. doi: 10.1016/j.patcog.2003.08.007 [19] 宫海梅. 图像隐藏算法的MATLAB实现[J]. 智能计算机与应用, 2016, 6(4): 60–62. doi: 10.3969/j.issn.2095-2163.2016.04.018GONG Haimei. Realization of image hiding algorithm based on MATLAB[J]. Intelligent Computer and Applications, 2016, 6(4): 60–62. doi: 10.3969/j.issn.2095-2163.2016.04.018 -













 下载:
下载:




 下载:
下载:
