The Multi-domain Union Clutter Suppression Algorithm Based on Robust Principal Component Analysis
-
摘要: 奇异值分解等传统算法在处理穿墙成像中的杂波抑制问题时,杂波消除不够彻底,目标成像质量不高,严重影响后续的目标检测与识别。为解决这一问题,该文基于鲁棒主成分分析理论,在回波域和图像域分别建立联合低秩稀疏模型,以光滑化快速交替线性化(SFAL)方法来求解模型,并对目标图像进行指数加权联乘多域图像融合处理,从而得到最终成像结果。仿真结果表明,该算法速度快、精度高,可有效改善目标成像质量,并能较好地满足穿墙成像的实时性和准确性要求。Abstract: In through-the-wall imaging, the clutter can not be eliminated completely through traditional algorithms, and affects seriously the subsequent target detection and recognition. To solve the problem, based on robust principal component analysis theory, a joint low-rank and sparse model is established in echo and image domain respectively. The models are solved by Smoothing Fast Alternating Linearization (SFAL) method. Then, the target images are dealt with exponentially weighted multiply multi-domain image fusion to obtain the final image. The simulation results indicate that the algorithm has great speed and accuracy with effective improvement on imaging quality of targets.
-
表 1 SFAL方法
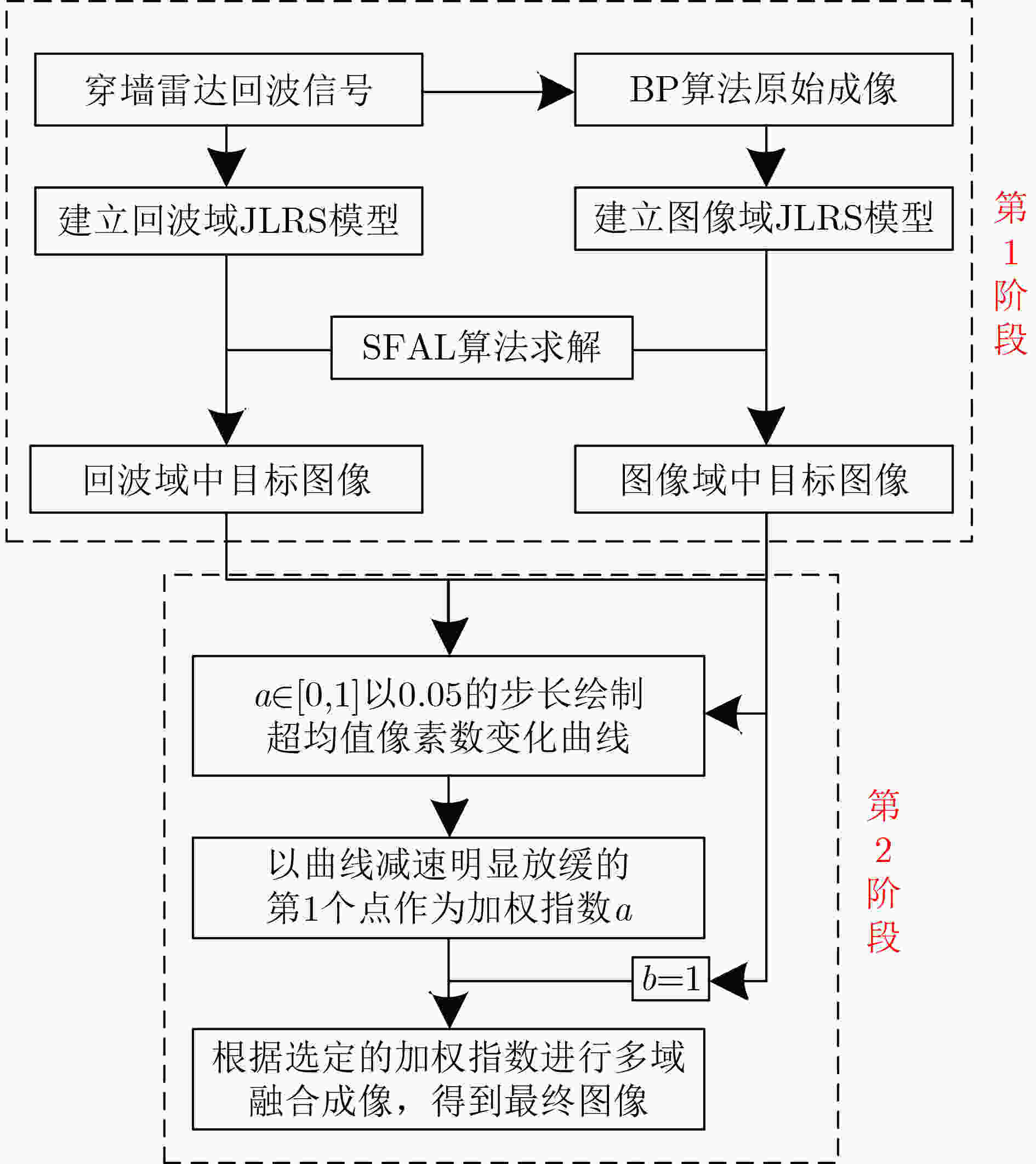
输入:2维图像矩阵$ {\mathbf{I}} \in {{\mathbf{R}}^{P \times Q}} $,凸函数$f({\mathbf{x}}) = {\left\| {\mathbf{x}} \right\|_ * }$,凸函数$ g({\mathbf{x}}) = \gamma {\left\| {{\mathbf{I}} - {\mathbf{x}}} \right\|_1} $,正则化参数$ \gamma = 1/\sqrt {\max (P,Q)} $; 输出:杂波分量矩阵${ {\mathbf{I} }_{\text{w} } } = { {\mathbf{x} }^{k{{ - } }1} }$,目标分量矩阵${ {\mathbf{I} }_{ {\text{tg} } } } = {\mathbf{I} } - { {\mathbf{x} }^{k{{ - } }1} }$。 (1) 初始化参数:$\alpha = \beta = {10^{ - 6}}$,$ {{\mathbf{x}}^0} = {{\mathbf{y}}^0} = {{\mathbf{z}}^1} = 0 $, $ {\mu _f} = {\mu _g} = 1 $, ${\eta _1} = 1$;$k = 1$。 (2) 根据式(12)和式(14)进行光滑化处理。 (3) 迭代解未收敛时执行步骤(4)到(7) (4) 根据式(18)和式(19)进行交替迭代; (5) 根据式(20)更新$\eta $; (6) 根据式(21)更新${\mathbf{z}}$; (7) $k \leftarrow k + 1$ (8) 结束循环 表 2 各方法性能对比
算法类型 SFAL APG EALM IALM 目标杂波比(dB) 12.15 11.22 11.95 11.27 迭代次数(次) 8 163 13 39 迭代时间(s) 0.1327 1.4603 8.3925 0.5512 表 3 各情况下的目标杂波比(dB)
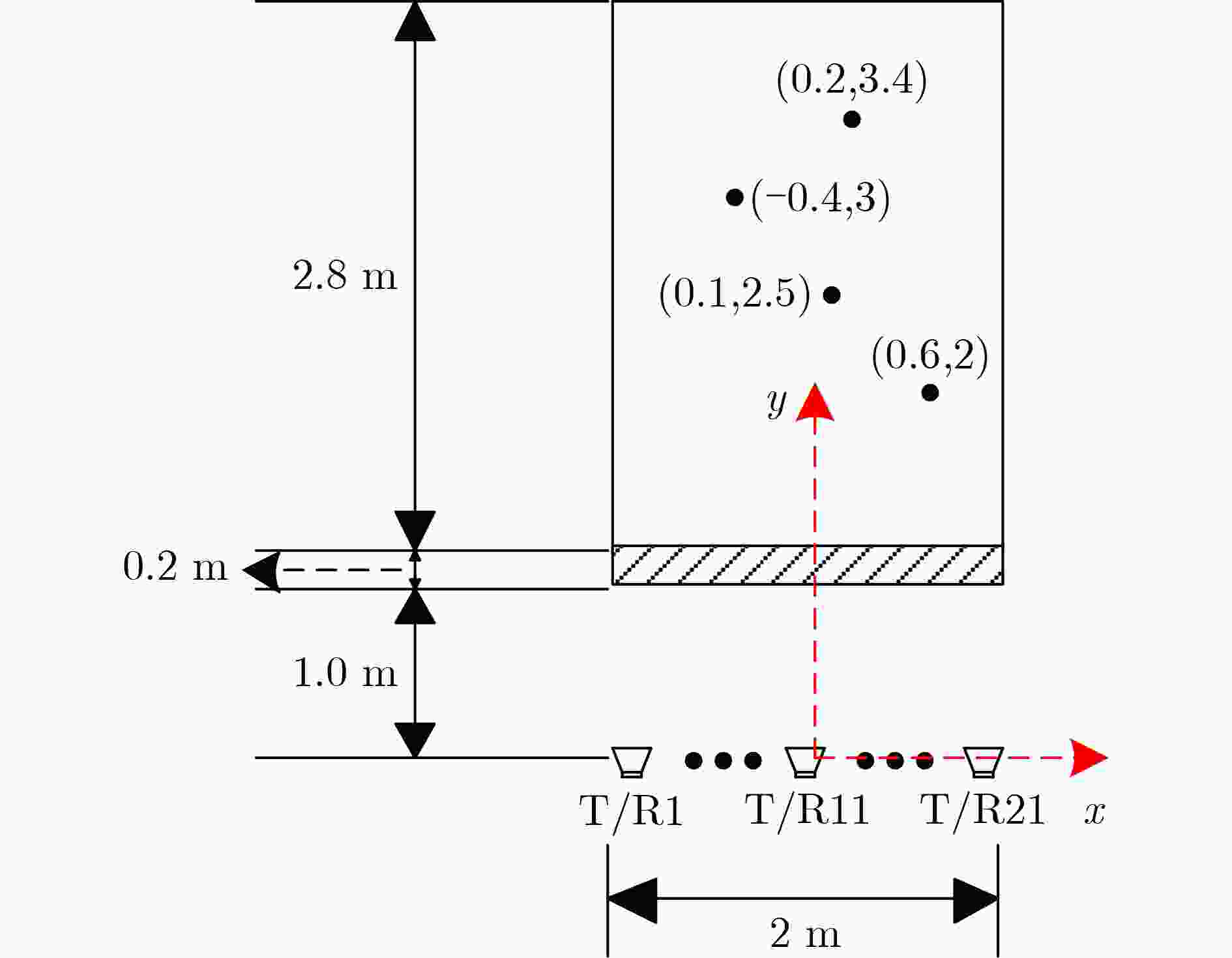
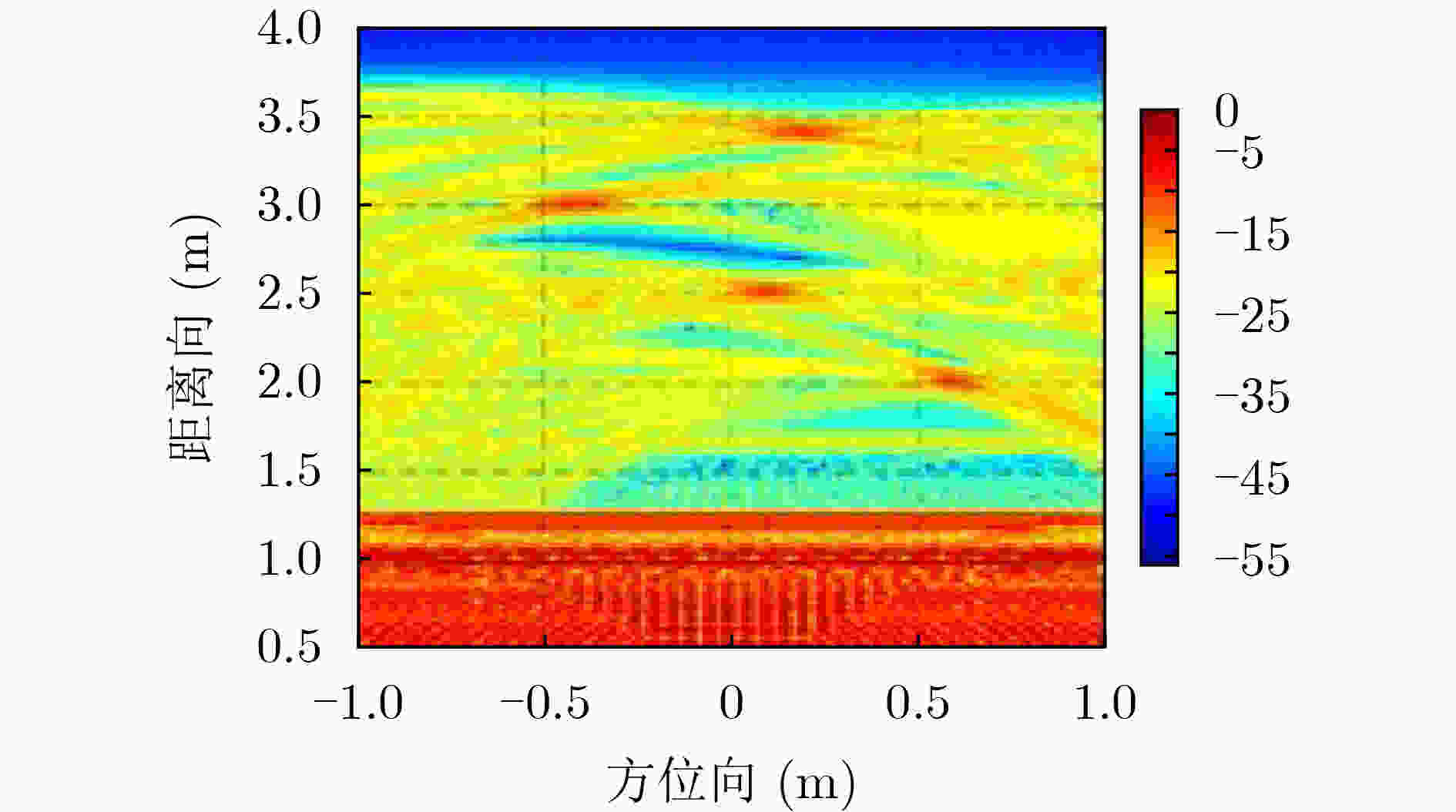
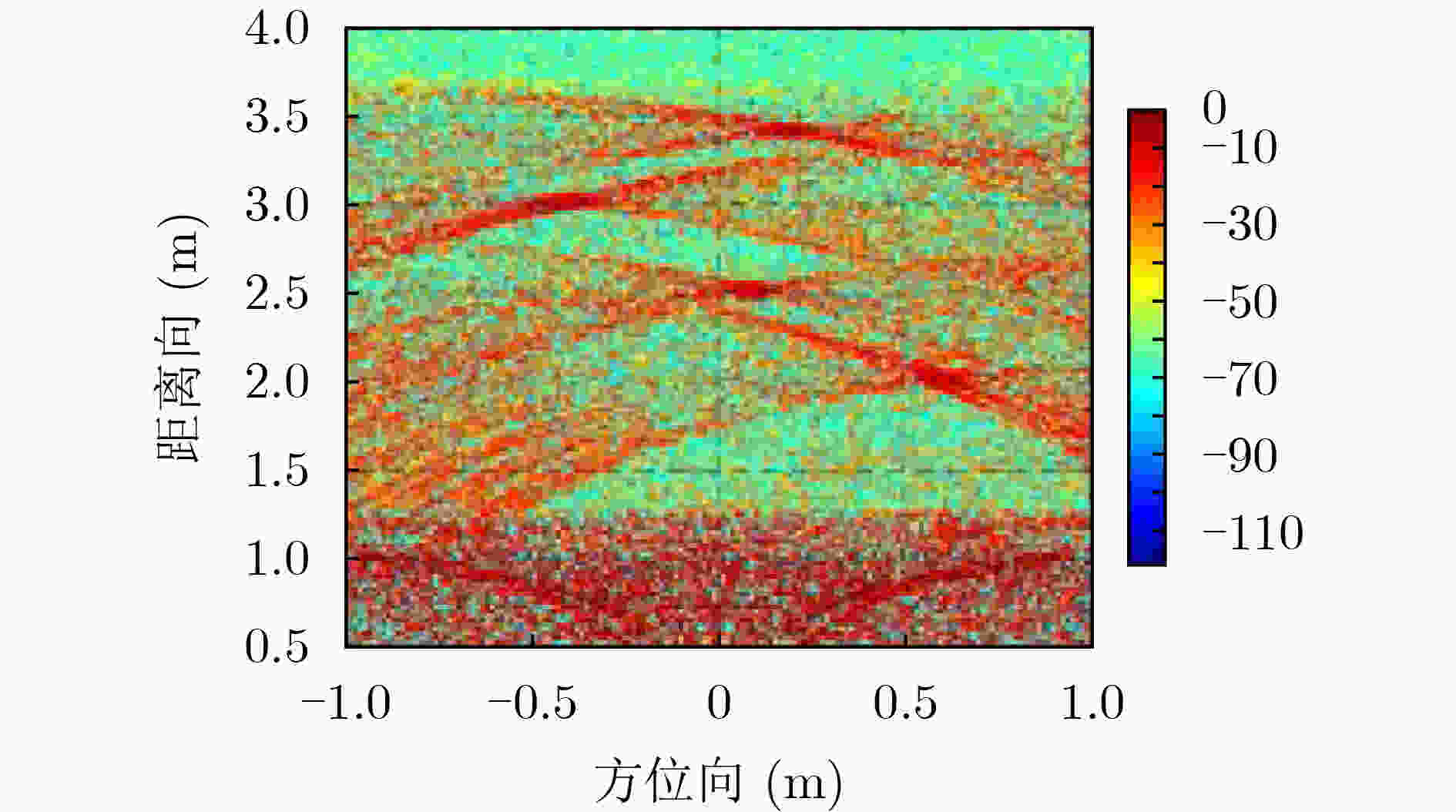
原始回波
成像多域联合
成像背景对消
成像SVD算法
成像目标杂波比 3.89 25.21 16.27 13.17 较原始成像改善 0 21.32 12.38 9.28 -
[1] 刘新, 阎焜, 杨光耀, 等. UWB-MIMO穿墙雷达三维成像与运动补偿算法研究[J]. 电子与信息学报, 2020, 42(9): 2253–2260. doi: 10.11999/JEIT190356XIN Liu, YAN Kun, YANG Guangyao, et al. Study on 3D imaging and motion compensation algorithm for UWB-MIMO through-wall radar[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2253–2260. doi: 10.11999/JEIT190356 [2] SHAO Wenyi and MCCOLLOUGH T. Advances in microwave near-field imaging: Prototypes, systems, and applications[J]. IEEE Microwave Magazine, 2020, 21(5): 94–119. doi: 10.1109/MMM.2020.2971375 [3] ZHOU Yi, HUANG Chen, LIU Hongqing, et al. Front-wall clutter removal in through-the-wall radar based on weighted nuclear norm minimization[J]. IEEE Geoscience and Remote Sensing Letters, To be published. doi: 10.1109/lgrs.2020.3034568. [4] DOĞU S, AKINCI M N, ÇAYÖREN M, et al. Truncated singular value decomposition for through-the-wall microwave imaging application[J]. IET Microwaves, Antennas & Propagation, 2020, 14(4): 260–267. doi: 10.1049/iet-map.2019.0677 [5] YE Guodong, PAN Chen, DONG Youxia, et al. Image encryption and hiding algorithm based on compressive sensing and random numbers insertion[J]. Signal Processing, 2020, 172: 107563. doi: 10.1016/j.sigpro.2020.107563 [6] LEIGSNERING M, DEBES C, and ZOUBIR A M. Compressive sensing in through-the-wall radar imaging[C]. Proceedings of 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 4008–4011. doi: 10.1109/ICASSP.2011.5947231. [7] VAN HA T, BOUTERDOUM A, and PHUNG S L. A matrix completion approach for wall-clutter mitigation in compressive radar imaging of indoor targets[C]. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, 2018: 1608–1612. doi: 10.1109/ICASSP.2018.8462000. [8] TANG V H, BOUZERDOUM A, and PHUNG S L. Compressive radar imaging of stationary indoor targets with low-rank plus jointly sparse and total variation regularizations[J]. IEEE Transactions on Image Processing, 2020, 29: 4598–4613. doi: 10.1109/tip.2020.2973819 [9] CANDÈS E J, LI Xiaodong, MA Yi, et al. Robust principal component analysis?[J]. Journal of the ACM, 2011, 58(3): 1–37. doi: 10.1145/1970392.1970395 [10] TIVIVE F H C and BOUZERDOUM A. An improved SVD-based wall clutter mitigation method for through-the-wall radar imaging[C]. The 14th Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Darmstadt, Germany, 2013: 430–434. doi: 10.1109/spawc.2013.6612086. [11] CANDES E J and TAO T. Near-optimal signal recovery from random projections: Universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425. doi: 10.1109/tit.2006.885507 [12] WEN Zaiwen, YIN Wotao, and ZHANG Yin. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm[J]. Mathematical Programming Computation, 2012, 4(4): 333–361. doi: 10.1007/s12532-012-0044-1 [13] CHANDRASEKARAN V, SANGHAVI S, PARRILO P A, et al. Rank-sparsity incoherence for matrix decomposition[J]. SIAM Journal on Optimization, 2011, 21(2): 572–596. doi: 10.1137/090761793 [14] LIN Zhouchen, GANESH A, WRIGHT J, et al. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix[R]. Coordinated Science Laboratory Report no. UILU-ENG-09-2214, DC-246, 2009: 1–18. [15] LIN Zhouchen, CHEN Minming, and MA Yi. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. arXiv preprint arXiv: 1009.5055, 2013. [16] 孙鑫. 超宽带穿墙雷达成像方法与技术研究[D]. [博士论文]. 国防科学技术大学, 2015.SUN Xin. Research on method and technique of ultra-wideband through-the-wall radar imaging[D]. [Ph. D. dissertation], National University of Defense Technology, 2015. [17] TANG V H, BOUZERDOUM A, and PHUNG S L. Multipolarization through-wall radar imaging using low-rank and jointly-sparse representations[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1763–1776. doi: 10.1109/tip.2017.2786462 [18] TIVIVE F H C and BOUZERDOUM A. Joint low-rank and sparse based image reconstruction for through-the-wall radar imaging[C]. The 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curacao, Holland, 2017: 1–5. doi: 10.1109/camsap.2017.8313110. [19] TANG V H, BOUZERDOUM A, PHUNG S L, et al. Radar imaging of stationary indoor targets using joint low-rank and sparsity constraints[C]. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 2016: 1412–1416. doi: 10.1109/icassp.2016.7471909. [20] 韩银萍, 刘丽, 王冰洁, 等. 基于鲁棒主成分分析的混沌穿墙成像雷达杂波抑制方法[J]. 电子器件, 2020, 43(1): 142–146. doi: 10.3969/j.issn.1005-9490.2020.01.029HAN Yinping, LIU Li, WANG Bingjie, et al. Clutter removal using robust principal component analysis for chaos through-wall imaging radar[J]. Chinese Journal of Electron Devices, 2020, 43(1): 142–146. doi: 10.3969/j.issn.1005-9490.2020.01.029 [21] GOLDFARB D, MA Shiqian, and SCHEINBERG K. Fast alternating linearization methods for minimizing the sum of two convex functions[J]. Mathematical Programming, 2013, 141(1/2): 349–382. doi: 10.1007/s10107-012-0530-2 [22] NESTEROV Y. Smooth minimization of non-smooth functions[J]. Mathematical Programming, 2005, 103(1): 127–152. doi: 10.1007/s10107-004-0552-5 [23] TRAN-DINH Q. Adaptive smoothing algorithms for nonsmooth composite convex minimization[J]. Computational Optimization and Applications, 2017, 66(3): 425–451. doi: 10.1007/s10589-016-9873-6 [24] TRAN-DINH Q and CEVHER V. A primal-dual algorithmic framework for constrained convex minimization[J]. arXiv preprint arXiv: 1406.5403, 2015. [25] NESTEROV Y. Introductory Lectures on Convex Optimization: A Basic Course[M]. New York: Kluwer Academic, 2003: 45–125. [26] JIA Yong, CUI Guolong, KONG Lingjiang, et al. Multichannel and multiview imaging approach to building layout determination of through-wall radar[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(5): 970–974. doi: 10.1109/lgrs.2013.2283778 [27] MCINTOSH B, VENKATARAMANAN S, and MAHALANOBIS A. Infrared target detection in cluttered environments by maximization of a target to clutter ratio (TCR) metric using a convolutional neural network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 57(1): 485–496. doi: 10.1109/TAES.2020.3024391 -





 下载:
下载:

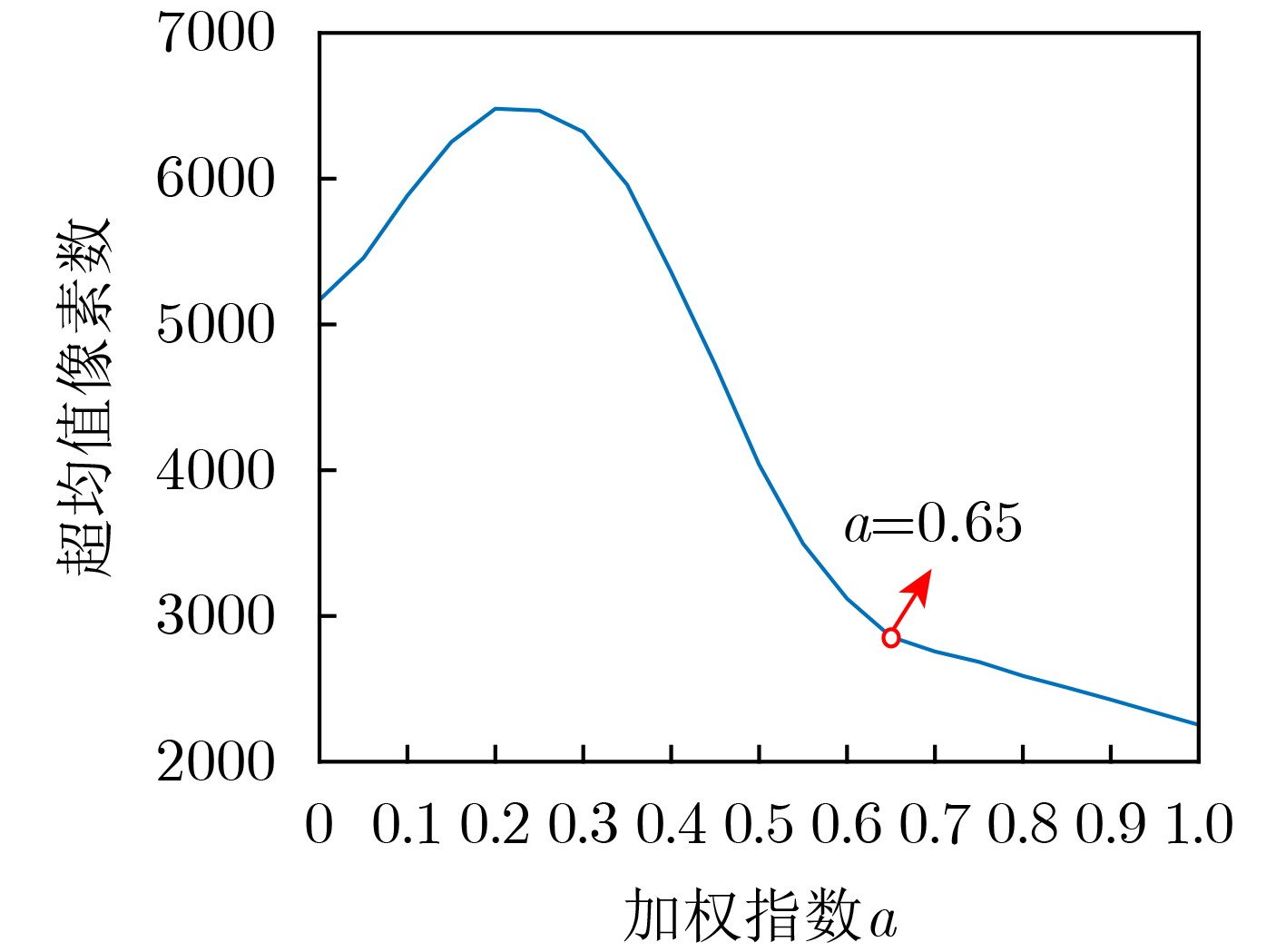
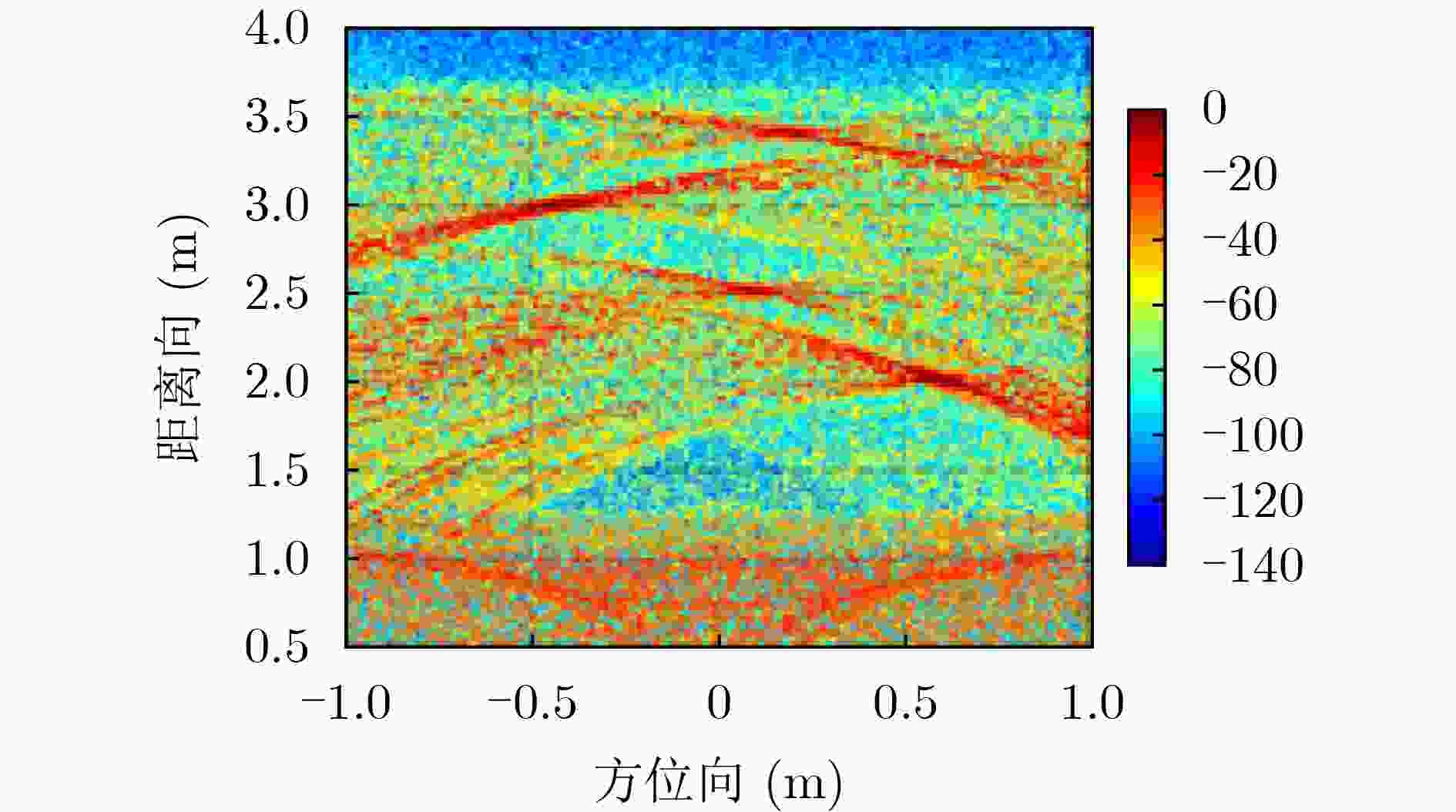
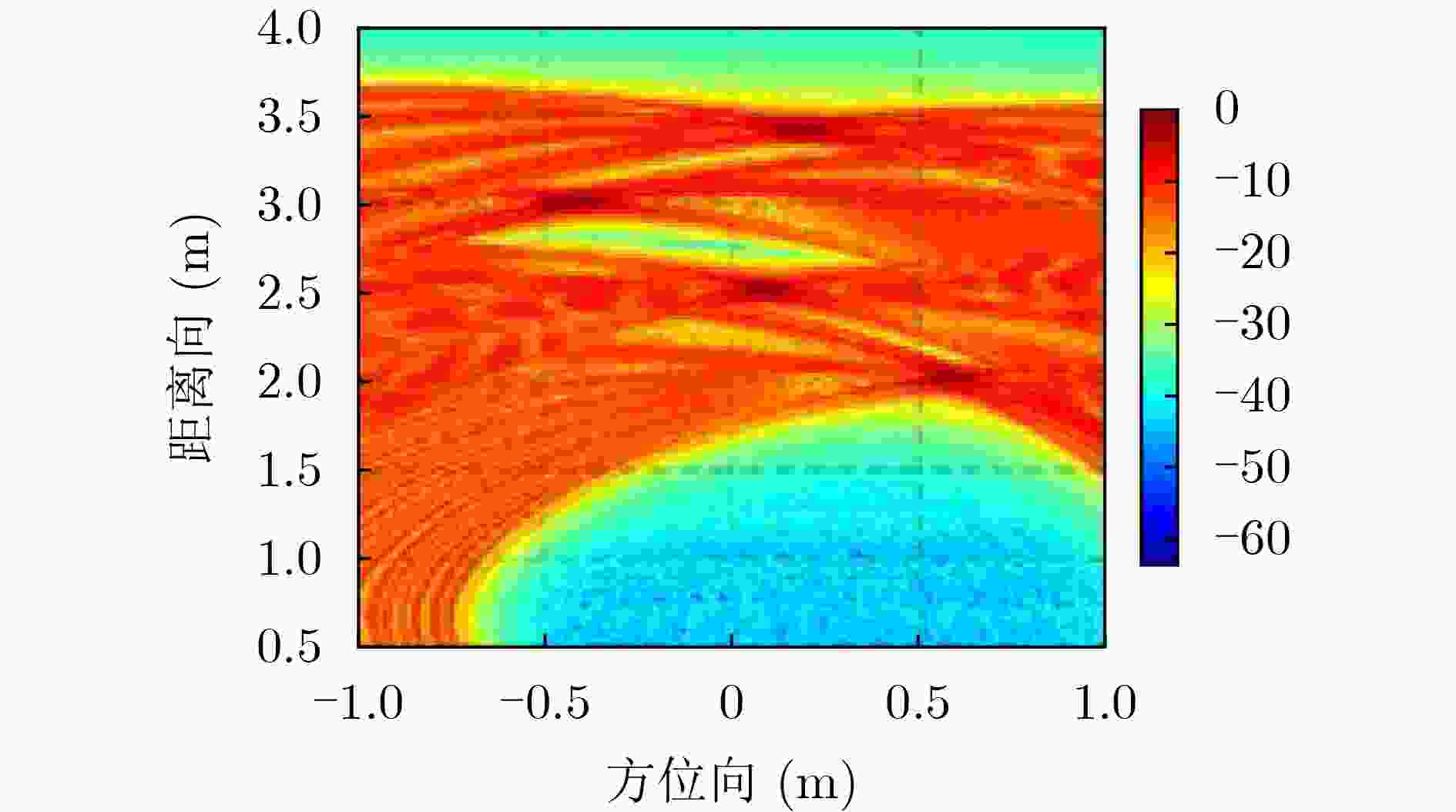
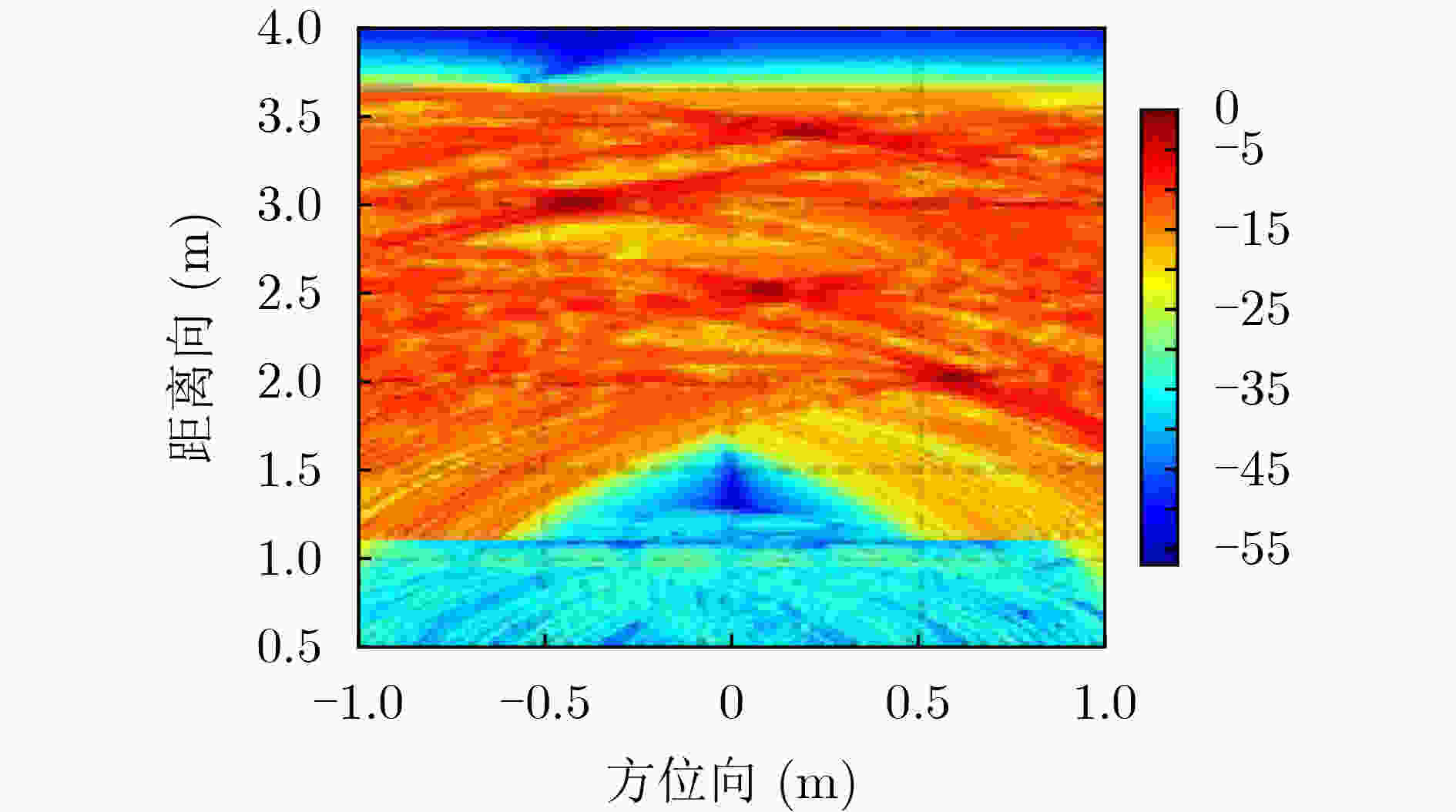


 下载:
下载:
