Artifact Optimization Algorithm for Pulmonary Electrical Impedance Tomography Based on Neighborhood Information and Fast FCM
-
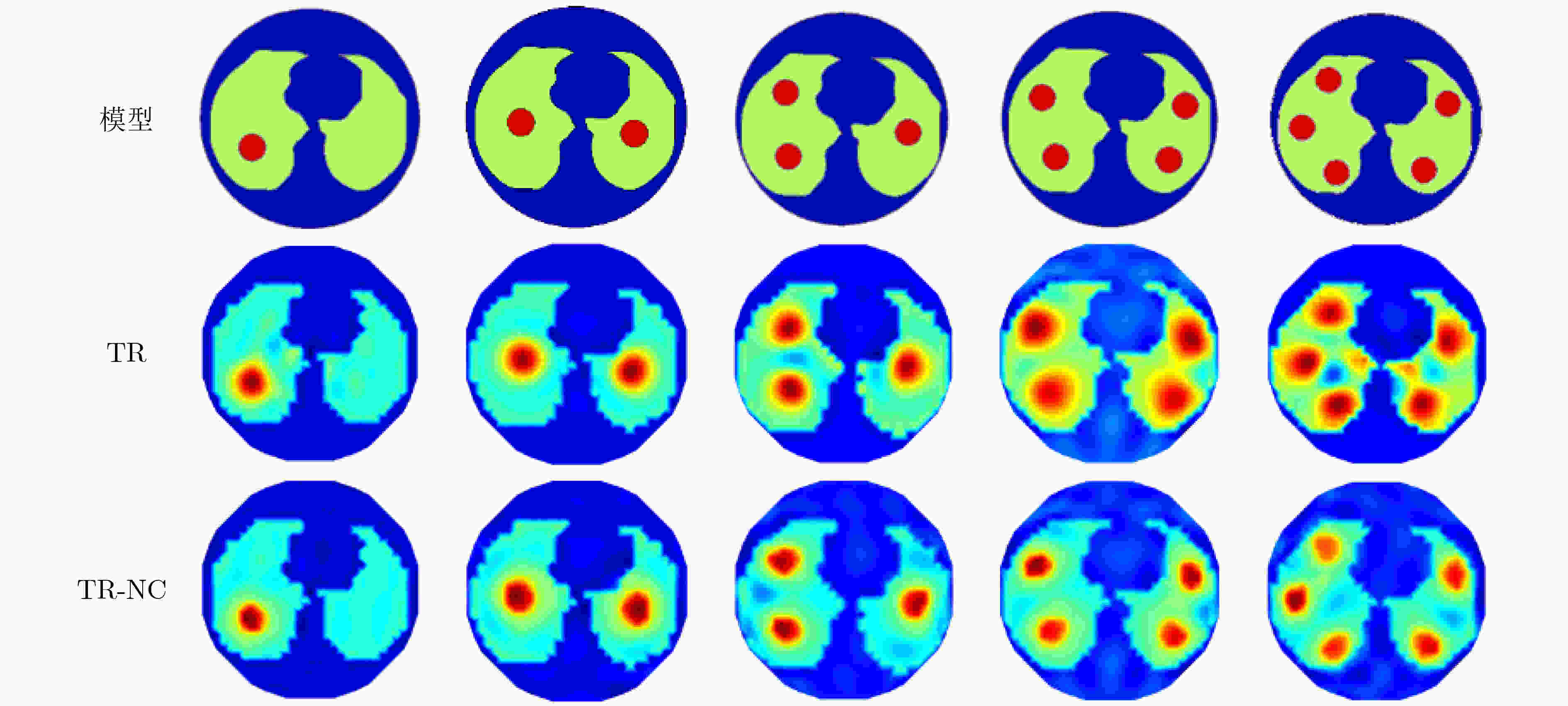
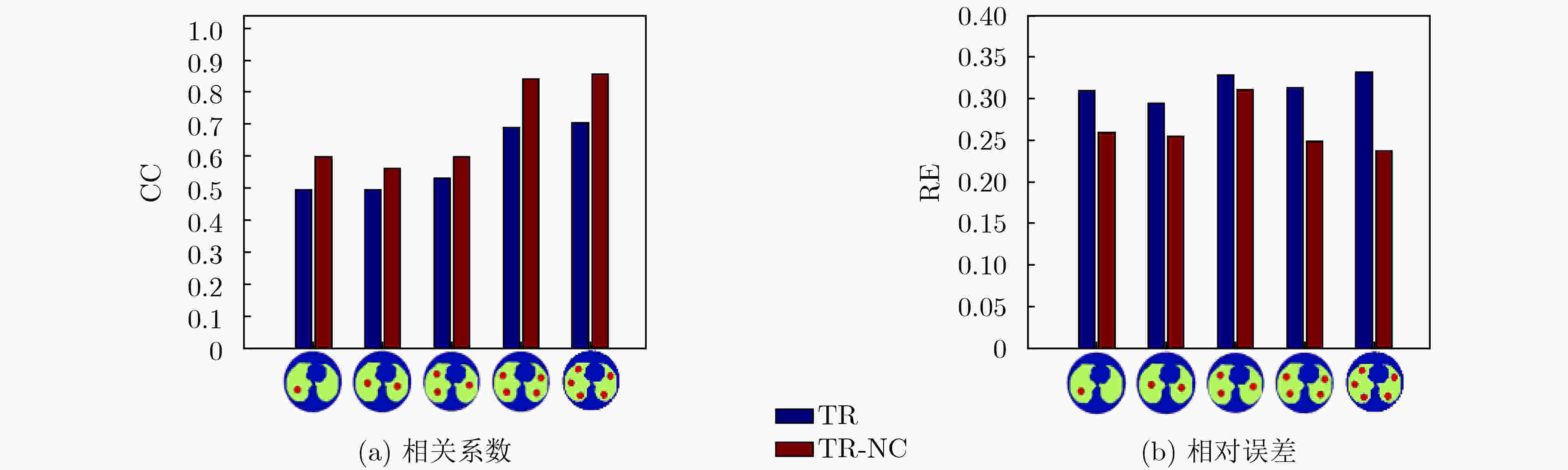
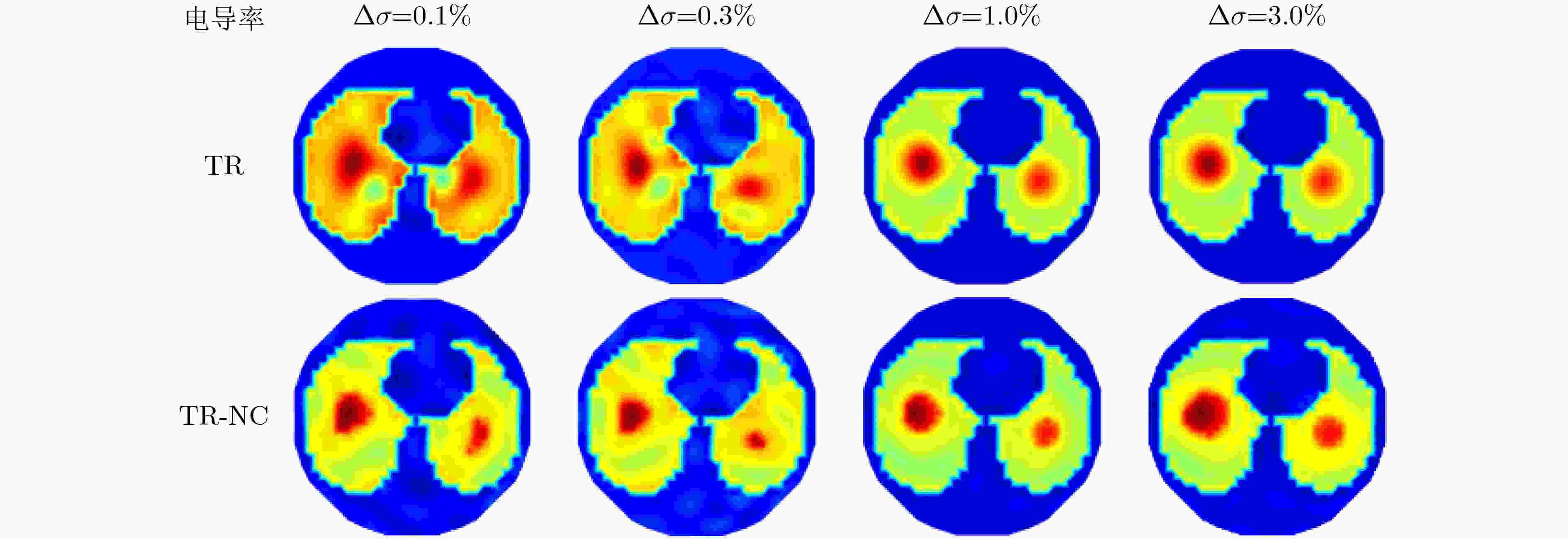
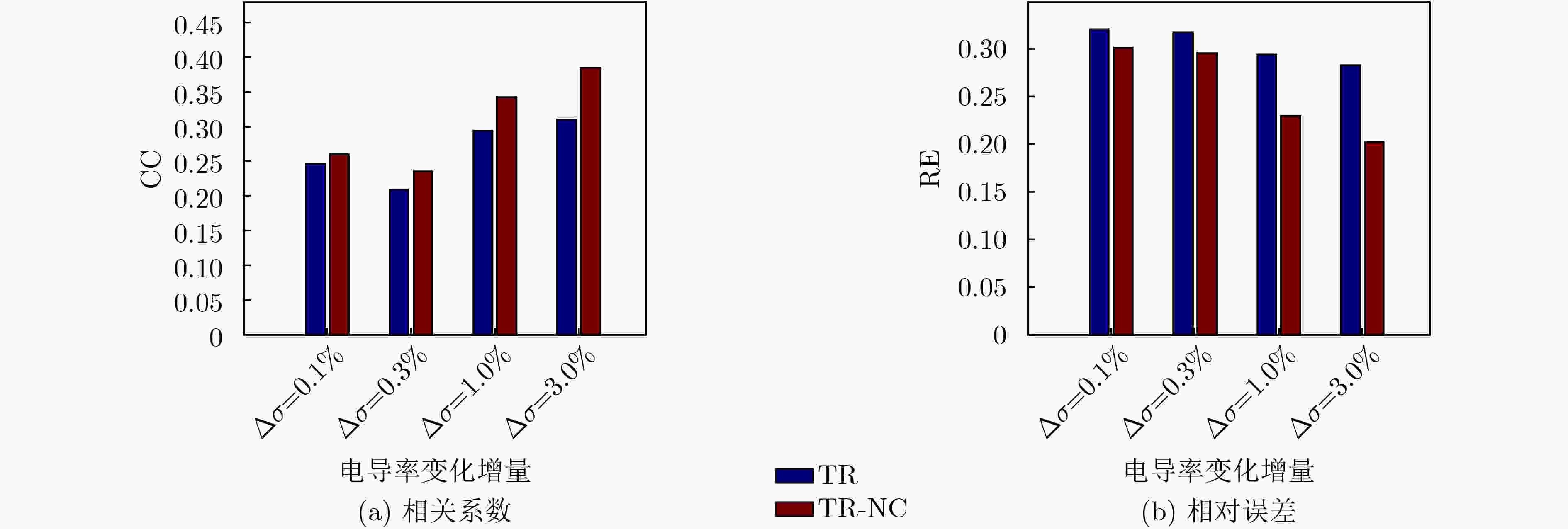
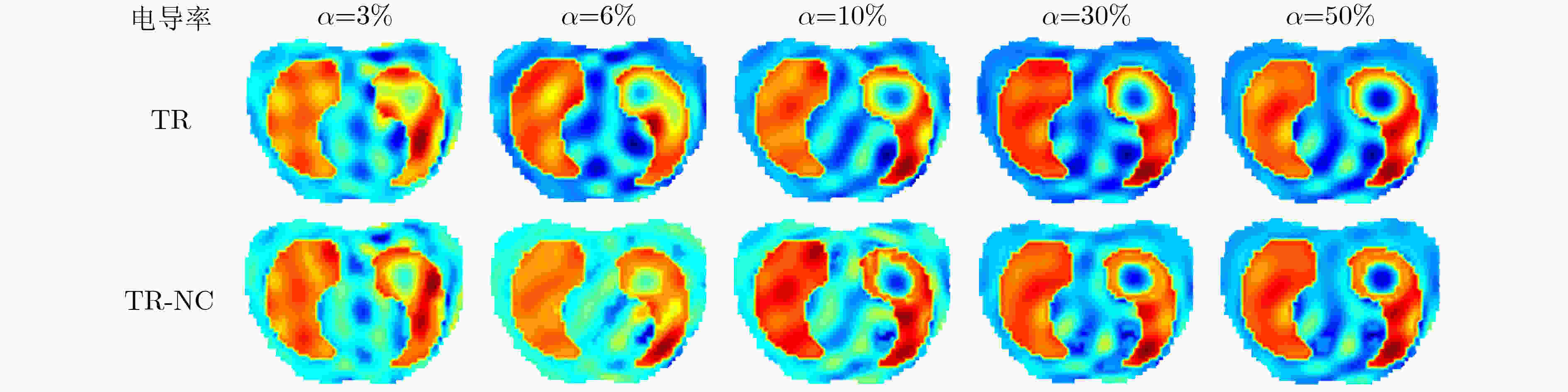
摘要: 针对电阻抗成像技术可视化过程中因“欠定”问题和“软场”效应所导致的重建图像伪迹问题,该文提出一种基于邻域信息和快速模糊C均值聚类(快速FCM)的无监督图像质量评价指标。基于该评价指标和Tikhonov正则化算法,提出了一种重建图像伪迹优化算法TR-NC。仿真结果表明,该算法能够有效地修正重建图像中的伪迹,修正后的重建图像的相关系数平均提高了18.45%,相对误差平均降低了22.2%;仿真体验实验结果表明,当目标电导率变化率大于30%时,该算法能够准确地检测到目标。由此可见,相比于传统的Tikhonov正则化算法,提出的修正算法在重建图像目标的数量和位置精确度方面都得到了显著提高,为电学层析技术在医学和工业等领域的应用实践提供了新的成像理论依据和技术参考。Abstract: To solve the problem of reconstruction image artifacts caused by the problem of "underdetermined" and the “soft field“ effect in the visualization process of electrical impedance tomography, an unsupervised image quality evaluation index based on neighborhood information and fast Fuzzy C-Means clustering (fast FCM) is proposed. Based on this evaluation index and Tikhonov regularization algorithm, a reconstruction image artifact optimization algorithm TR-NC is proposed. Simulation results show that the proposed algorithm can effectively correct artifacts in the reconstructed image, and the correlation coefficient of the modified reconstructed image has increased by 18.45% on average, and the relative error has reduced by 22.2% on average. Simulation experimental results show that the proposed algorithm can accurately detect the target when the change rate of target conductivity is more than 30%. It is shown that compared with the traditional Tikhonov regularization algorithm, the proposed modified algorithm TR-NC has been significantly improved in the number and position accuracy of reconstruction image targets, which provides a new imaging theoretical basis and technical reference for the application of electrical tomography technology to medical and industrial fields.
-
表 1 TR-NC的计算流程
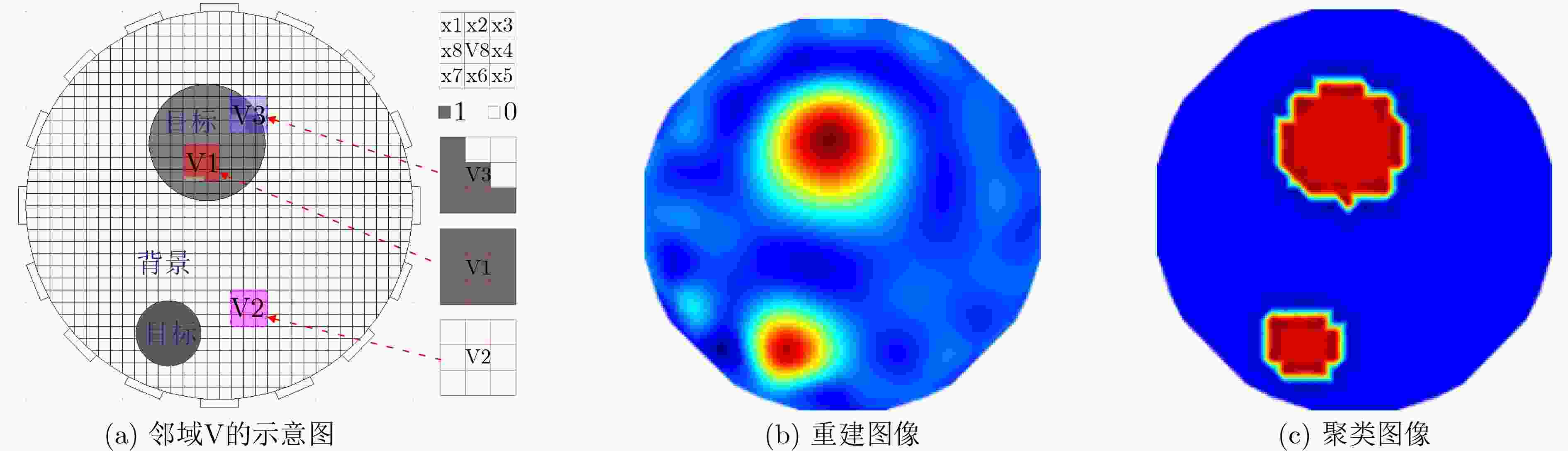
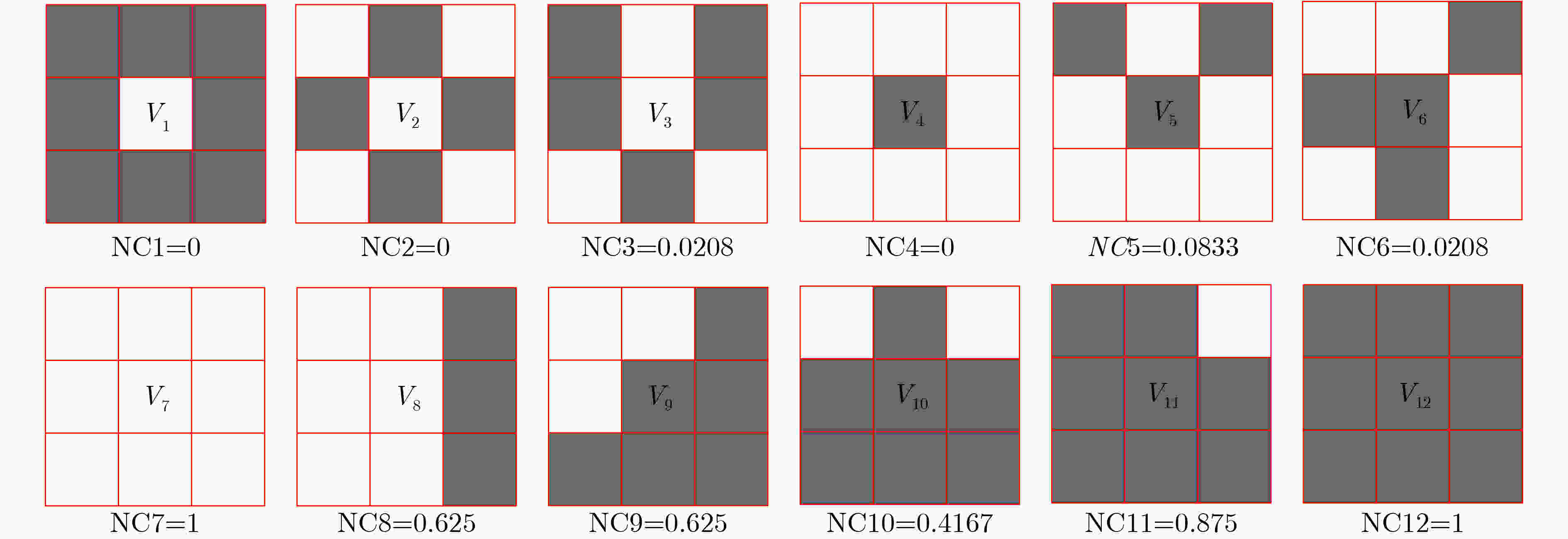
输入:边界测量值U,灵敏度矩阵S 输出:灰度向量g 步骤:1.利用TR得1次成像灰度g0; 2.利用f-FCM将灰度g0聚为2类并将灰度二值化为0和1; 3.计算NC值,并据此生成对角矩阵D; 4.将D代入式(12)进行求解,得到灰度值g。 -
[1] SHI Yanyan, ZHANG Xu, WANG Meng, et al. An adaptive non-convex hybrid total variation regularization method for image reconstruction in electrical impedance tomography[J]. Flow Measurement and Instrumentation, 2021, 79: 101937. doi: 10.1016/j.flowmeasinst.2021.101937 [2] 冯慈璋, 马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.FENG Cizhang and MA Xikui. An Introduction to Engineering Electromagnetic Fields[M]. Beijing: Higher Education Press, 2000. [3] BIAŁKA S, COPIK M, RYBCZYK K, et al. Electrical impedance tomography for diagnosis and monitoring of pulmonary function disorders in the intensive care unit-case report and review of literature[J]. Anaesthesiology Intensive Theraphy, 2017, 49(3): 222–226. doi: 10.5603/AIT.2017.0040 [4] 褚猛丽. 三维电阻抗图像重建模型优化研究[D]. [硕士论文], 天津科技大学, 2017.CHU Mengli. Research on model optimization of three-dimensional electrical impedance image reconstruction[D]. [Master dissertation], Tianjin University of science and technology, 2017. [5] YANG Yunjie, JIA Jiabin, SMITH S, et al. A miniature electrical impedance tomography sensor and 3-D image reconstruction for cell imaging[J]. IEEE Sensors Journal, 2017, 17(2): 514–523. doi: 10.1109/JSEN.2016.2631263 [6] YAO Jiafeng, KODERA T, OBARA H, et al. Spatial concentration distribution analysis of cells in electrode-multilayered microchannel by dielectric property measurement[J]. Biomicrofluidics, 2015, 9(4): 044129. doi: 10.1063/1.4929824 [7] TING C H, LIN K H, CHIU C H, et al. Simultaneous time-of-flight PET/MR identifies the hepatic 90Y-resin distribution after radioembolization[J]. Clinical Nuclear Medicine, 2020, 45(2): e92–e93. doi: 10.1097/RLU.0000000000002850 [8] 李英. 电阻层析成像技术软场特性及图像重建算法研究[D]. [硕士论文], 浙江大学, 2003.LI Ying. Study on the soft-field characteristic and image reconstruction algorithm of electrical resistance tomography[D]. [Master dissertation], Zhejiang University, 2003. [9] 罗辞勇, 朱清友. 改进的电阻抗反投影成像算法[J]. 重庆大学学报, 2009, 32(3): 243–246. doi: 10.11835/j.issn.1000-582X.2009.03.001LUO Ciyong and ZHU Qingyou. An improved back-projection algorithm for electrical impedance tomography[J]. Journal of Chongqing University, 2009, 32(3): 243–246. doi: 10.11835/j.issn.1000-582X.2009.03.001 [10] 李冬晔. 电阻抗成像技术正则化算法的研究[D]. [硕士论文], 南京邮电大学, 2016.LEE J. Regularization algorithm research of electrical impedance tomography[D]. [Master dissertation], Nanjing University of Posts and Telecommunications, 2016. [11] 岳士弘, 张洋洋, 赵愉, 等. 电学层析成像的灵敏度系数更新算法[J]. 天津大学学报:自然科学与工程技术版, 2017, 50(12): 1227–1234.YUE Shihong, ZHANG Yangyang, ZHAO Yu, et al. Updating algorithm for sensitivity coefficient of electrical tomography[J]. Journal of Tianjin University:Science and Technology, 2017, 50(12): 1227–1234. [12] 陈瑞娟, 吴伟巍, 李芳, 等. 基于结构先验信息的磁探测电阻抗成像算法研究[J]. 仪器仪表学报, 2020, 41(5): 196–204. doi: 10.19650/j.cnki.cjsi.J1905840CHEN Ruijuan, WU Weiwei, LI Fang, et al. Research on magnetic detection electrical impedance tomography based on structural prior information[J]. Chinese Journal of Scientific Instrument, 2020, 41(5): 196–204. doi: 10.19650/j.cnki.cjsi.J1905840 [13] AUGUSTIN X, KIRCHER M, DÖSSEL O, et al. Estimating regional pulmonary blood flow in EIT with regularized deconvolution with a Tikhonov regularization[J]. Current Directions in Biomedical Engineering, 2020, 6(3): 60–63. doi: 10.1515/cdbme-2020-3016 [14] 吴新杰, 闫诗雨, 徐攀峰, 等. 基于稀疏度自适应压缩感知的电容层析成像图像重建算法[J]. 电子与信息学报, 2018, 40(5): 1250–1257. doi: 10.11999/JEIT170794WU Xinjie, YAN Shiyu, XU Panfeng, et al. Image reconstruction algorithm for electrical capacitance tomography based on sparsity adaptive compressed sensing[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1250–1257. doi: 10.11999/JEIT170794 [15] 叶明, 李晓丞, 刘凯, 等. 一种基于U2-Net模型的电阻抗成像方法[J]. 仪器仪表学报, 2021, 42(2): 235–243. doi: 10.19650/j.cnki.cjsi.J2007065YE Ming, LI Xiaocheng, LIU Kai, et al. Image reconstruction method for electrical impedance tomography using U2-Net[J]. Chinese Journal of Scientific Instrument, 2021, 42(2): 235–243. doi: 10.19650/j.cnki.cjsi.J2007065 [16] 王琦, 张鹏程, 汪剑鸣, 等. 基于块稀疏的电阻抗成像算法[J]. 电子与信息学报, 2018, 40(3): 676–682. doi: 10.11999/JEIT170425WANG Qi, ZHANG Pengcheng, WANG Jianming, et al. Block-sparse reconstruction for electrical impedance tomography[J]. Journal of Electronics &Information Technology, 2018, 40(3): 676–682. doi: 10.11999/JEIT170425 -





 下载:
下载:



 下载:
下载:
