基于人工神经网络特征向量提取的FF-APUF攻击方法

马雪娇; 李刚

doi:10.11999/JEIT210614

基于人工神经网络特征向量提取的FF-APUF攻击方法

doi: 10.11999/JEIT210614

马雪娇¹,
李刚^2, ,

1.
温州理工学院数据科学与人工智能学院温州 325035
2.
温州大学电气与电子工程学院温州 325035

基金项目: 国家重点研发计划(2018YFB2202100)，国家自然科学基金(61874078, 61904125)，温州市基础性科研项目(G20190006, G20190003)

详细信息

作者简介:
马雪娇：女，1991年生，助教，研究方向为物理不可克隆函数攻击与防御

李刚：男，1988年生，讲师，研究方向为密码芯片攻击防御理论及VLSI实现

通讯作者:
李刚　ligang@wzu.edu.cn

中图分类号: TN918; TP331
计量
- 文章访问数: 1057
- HTML全文浏览量: 498
- PDF下载量: 83
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-22
- 修回日期: 2021-08-12
- 网络出版日期: 2021-08-23
- 刊出日期: 2021-09-16

ANN Feature Vector Extraction Based Attack Method for Flip-Flop Based Arbiter Physical Unclonable Function

Xuejiao MA¹,
Gang LI^{2
, ,}

1.
School of Data Science and Artificial Intelligence, Wenzhou University of Technology, Wenzhou 325035, China
2.
College of Electrical and Electronic Engineering, Wenzhou University, Wenzhou 325035, China

Funds: The National Key Research and Development Program of China (2018YFB2202100), The National Natural Science Foundation of China (61874078, 61904125), The Wenzhou Basic Scientific Research Projects (G20190006, G20190003)

摘要

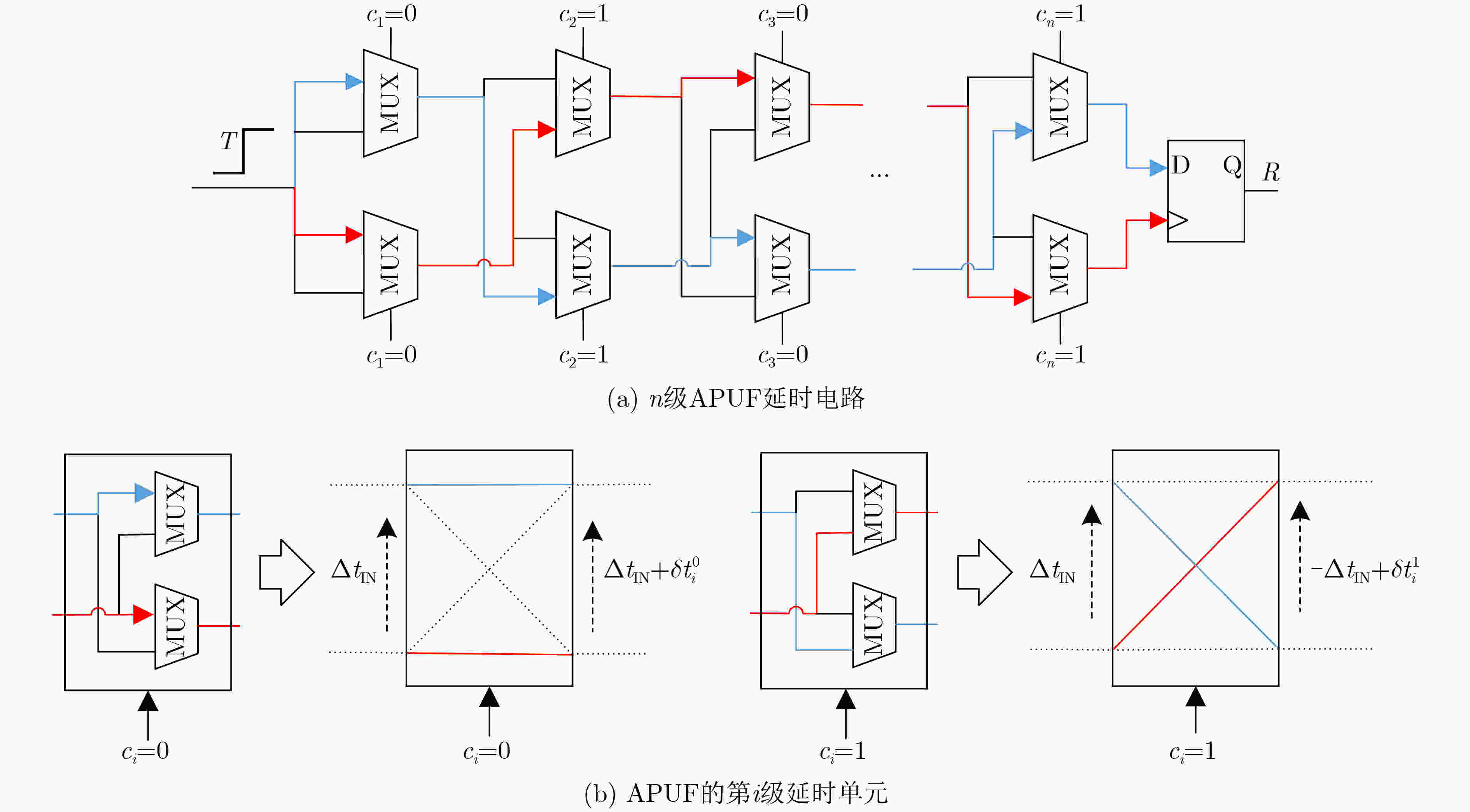
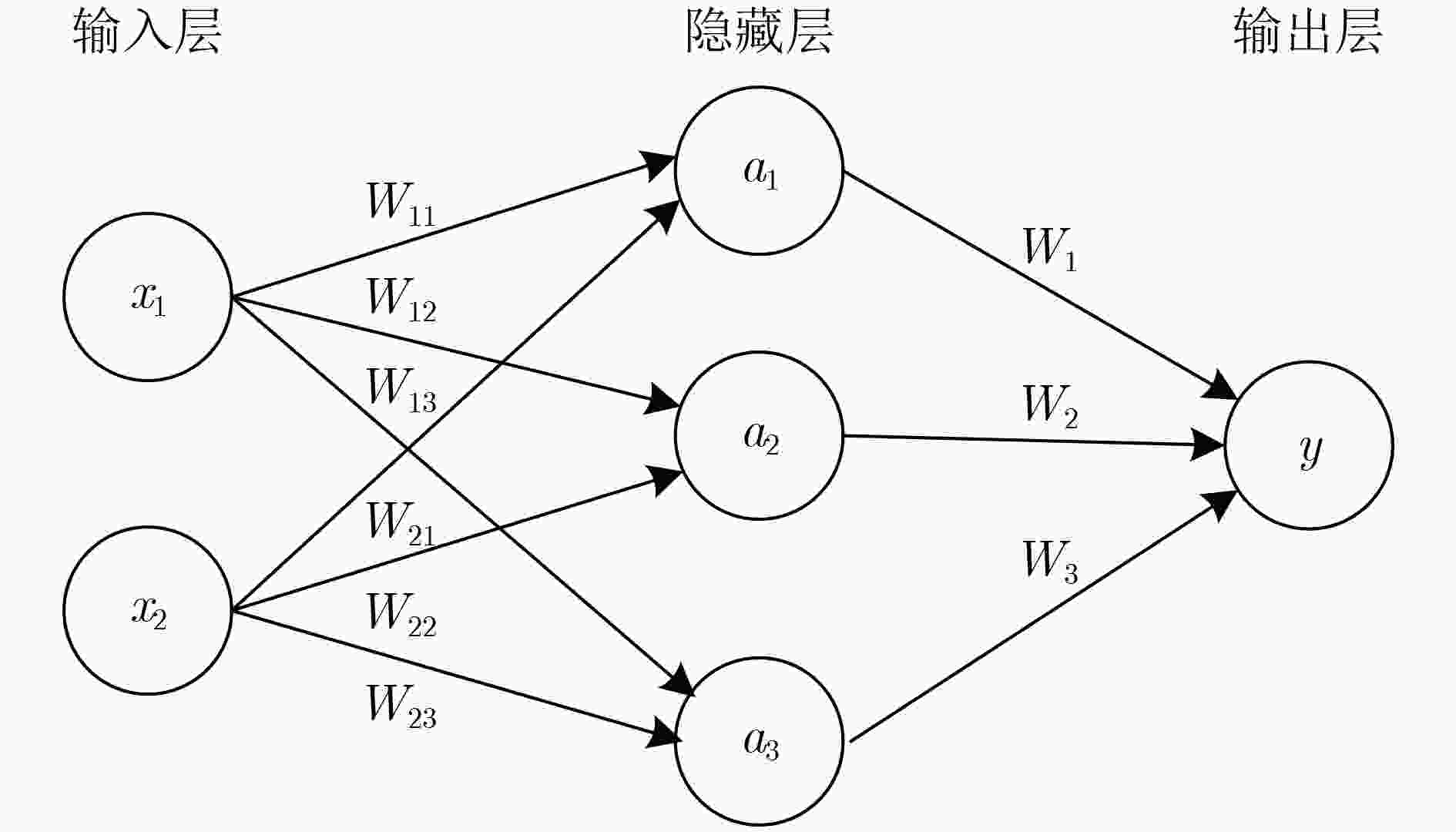
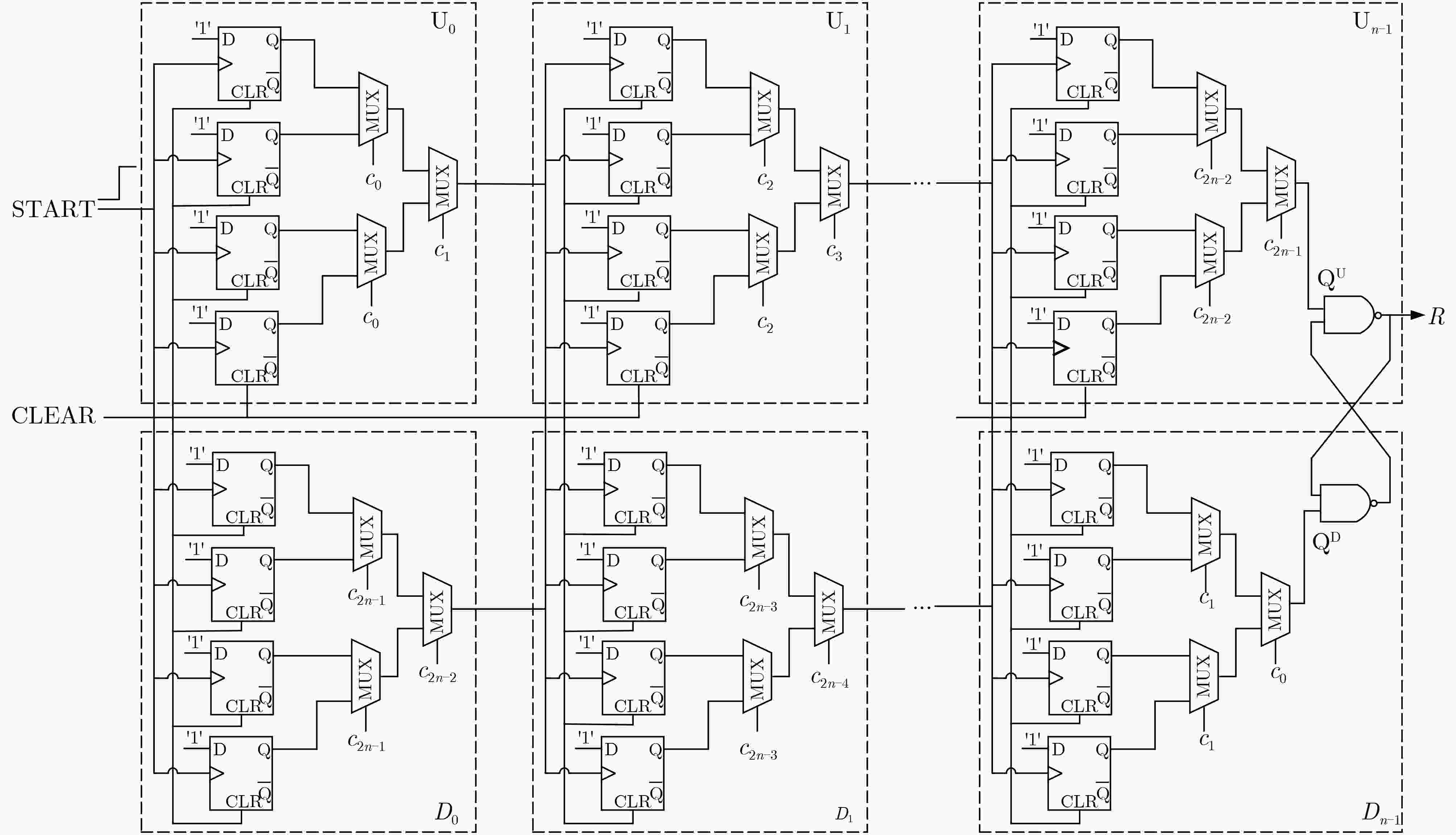
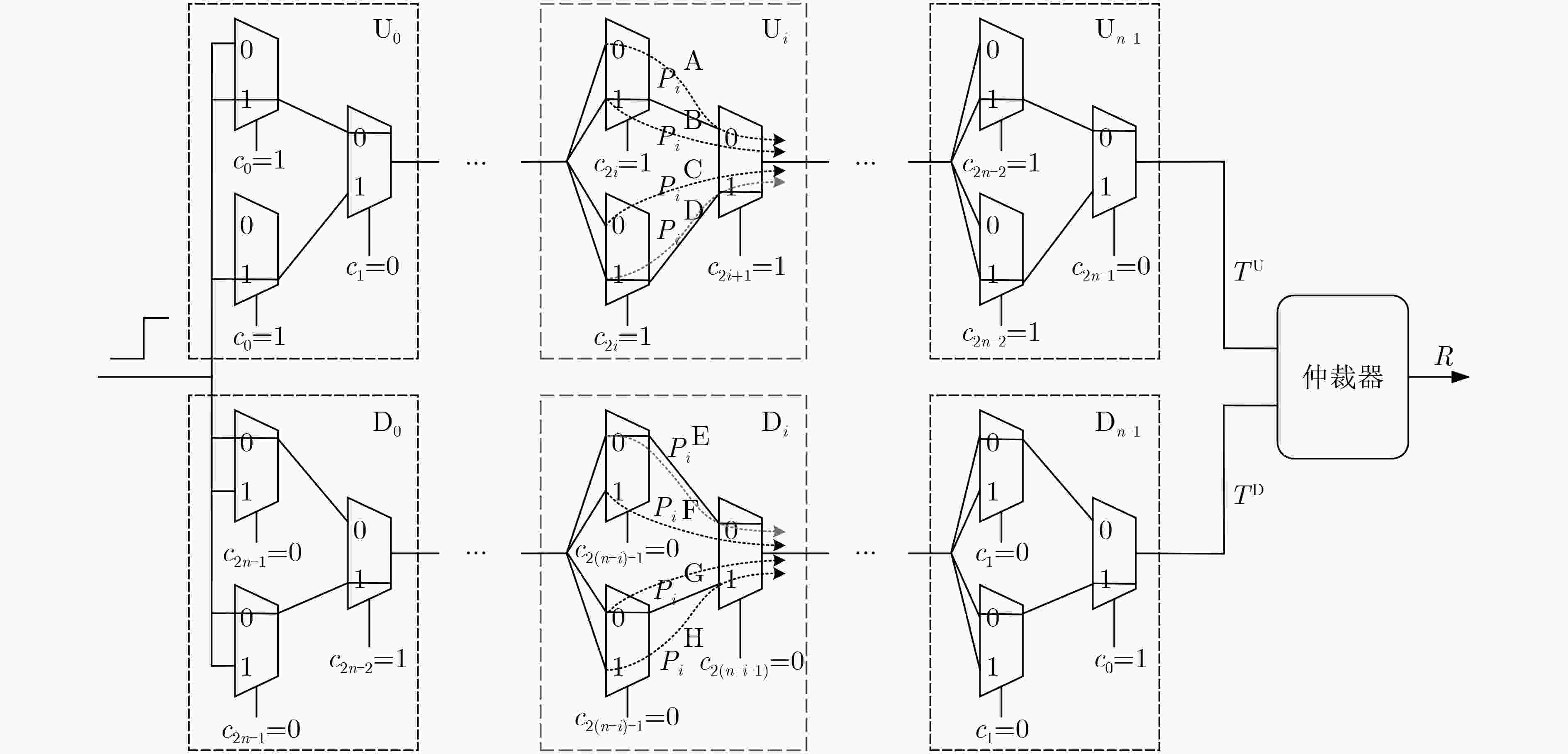
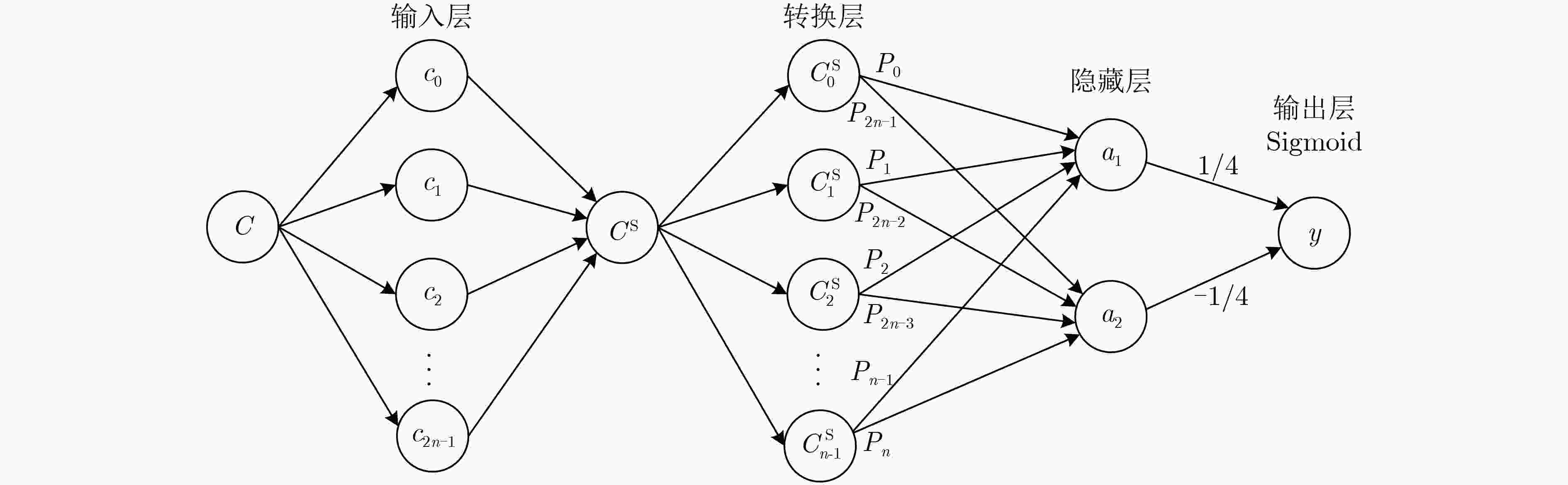
摘要: 为评估物理不可克隆函数(PUF)的安全性，需针对不同的PUF结构设计相应的攻击方法。该文通过对强PUF电路结构和工作机理的研究，利用人工神经网络(ANN)提出一种针对触发器-仲裁器物理不可克隆函数(FF-APUF)的有效攻击方法。首先，根据FF-APUF电路结构，利用多维数组构建电路延时模型；然后，对FF-APUF的二进制激励进行邻位划分，将划分后的激励转换为十进制并表示为行向量，实现特征向量提取；最后，基于提取的特征向量利用ANN构建攻击模型并通过后向传播算法获得最优参数。实验结果表明，相同条件下攻击预测率均高于其他3种常用的机器学习方法，尤其当激励响应对(CRP)数量较少、激励位数较多时，优势更加明显。当激励位数为128、CRP个数为100和500时，平均攻击预测率分别提高36.0%和16.1%。此外，该方法具有良好的鲁棒性和可扩展性，不同噪声系数下攻击预测率与可靠性相差最大仅0.32%。
- 物理不可克隆函数 /
- 触发器-仲裁器物理不可克隆函数 /
- 人工神经网络 /
- 特征向量提取
Abstract: In order to evaluate the security of Physical Unclonable Function (PUF), it is necessary to put forward corresponding attack methods for different PUF structures. By studying the structure and working mechanism of Flip-Flop based Arbiter Physical Unclonable Function (FF-APUF), an effective attack method against FF-APUF is proposed based on Artificial Neural Network (ANN) in this paper. Firstly, according to the circuit structure, the delay model of FF-APUF is established by using multidimensional array. Secondly, all binary challenge bits are divided by two adjacent bits which are converted to a decimal, and then the challenges are expressed as a row vector to extract the feature vector. Finally, based on the extracted feature vectors, the attack model is constructed by ANN, and the optimal parameters are obtained by back propagation algorithm. The experimental results show that the prediction accuracy of the proposed method is higher than other three common machine learning methods under the same conditions. The attack advantage is more obvious, especially when the number of Challenge Response Pairs (CRP) is less and the bit number of challenges is large. For example, when the number of challenge bit is 128, and the number of CRPs is 100 and 500, the average attack prediction accuracy increased by 36.0% and 16.1% respectively. In addition, the proposed method has good robustness and scalability, and the maximum difference of attack prediction rate and reliability is only 0.32% under different noise.
- Physical Unclonable Function (PUF) /
- Flip-Flop based Arbiter Physical Unclonable Function (FF-APUF) /
- Artificial Neural Network (ANN) /
- Feature vector extraction

HTML全文

图 1 APUF电路结构

下载: 全尺寸图片幻灯片

图 2 3层神经网络结构

下载: 全尺寸图片幻灯片

图 3 FF-APUF电路结构

下载: 全尺寸图片幻灯片

图 4 简化的FF-APUF电路结构

下载: 全尺寸图片幻灯片

图 5 基于ANN的FF-APUF攻击模型

下载: 全尺寸图片幻灯片

图 6 预测误差与N_CRP/(n+1)的关系

下载: 全尺寸图片幻灯片

图 7 N_CRP与迭代次数的关系

下载: 全尺寸图片幻灯片

表 1 ANN特性参数及选取

特性参数	参数选取
初始化权值	随机正态分布
初始化偏置	零向量
优化器	Adam或RMSProp
损失函数	最小均方误差
正则化	L2
输出层激活函数	Sigmoid

下载: 导出CSV

表 2 攻击方法及预测率(%)

CRP个数	激励位数	APUF				FF-APUF
CRP个数	激励位数	LR	SVM	GNB	本文方法	LR	SVM	GNB	本文方法
100	32	81.7	83.7	82.7	90.1	77.3	76.0	73.6	81.4
	64	77.7	74.6	78.6	80.3	66.4	77.0	75.7	80.1
	128	74.0	70.3	73.3	76.1	59.6	57.3	57.0	78.8
500	32	94.0	95.5	87.0	97.1	93.1	92.4	87.4	96.8
	64	93.7	92.4	84.6	96.2	88.3	87.1	82.4	95.7
	128	85.5	85.5	80.9	89.6	79.9	76.8	74.1	89.2
1000	32	97.5	97.9	92.2	99.5	97.0	97.3	90.2	99.0
	64	95.8	95.1	89.9	97.5	94.3	93.1	86.9	95.5
	128	93.4	91.7	86.2	93.5	89.2	87.1	81.5	91.5
2000	32	98.7	98.4	93.4	99.3	98.3	98.4	92.1	99.5
	64	97.8	97.1	92.8	98.8	96.7	96.8	90.3	97.8
	128	95.4	95.4	89.4	97.0	94.2	93.2	85.8	96.5
5000	32	99.4	99.2	95.6	99.7	99.0	99.2	95.5	99.6
	64	99.0	98.8	93.4	99.2	98.5	98.5	94.1	98.9
	128	98.2	98.2	92.5	98.7	97.7	97.1	90.7	97.9
10000	32	99.7	99.4	96.7	99.9	99.4	99.4	94.7	99.7
	64	99.3	99.1	95.8	99.6	99.2	99.2	94.4	99.6
	128	99.0	98.9	95.2	99.4	98.6	98.7	94.0	99.0

下载: 导出CSV

表 3 所提方法相比其他方法预测率的提升比例(%)

CRP个数	激励位数	APUF				FF-APUF
CRP个数	激励位数	LR	SVM	GNB	平均值	LR	SVM	GNB	平均值
100	32	10.3	7.6	8.9	9.0	5.3	7.1	10.6	7.7
	64	3.3	7.6	2.2	4.4	20.6	4.0	5.8	10.2
	128	2.8	8.3	3.8	5.0	32.2	37.5	38.2	36.0
500	32	3.3	1.7	11.6	5.5	4.0	4.8	10.8	6.5
	64	2.7	4.1	13.7	6.8	8.4	9.9	16.1	11.5
	128	4.8	4.8	10.8	6.8	11.6	16.1	20.4	16.1
1000	32	2.1	1.6	7.9	3.9	2.1	1.7	9.8	4.5
	64	1.8	2.5	8.5	4.3	1.3	2.6	9.9	4.6
	128	0.1	2.0	8.5	3.5	2.6	5.1	12.3	6.6
2000	32	0.6	0.9	6.3	2.6	1.2	1.1	8.0	3.5
	64	1.0	1.8	6.5	3.1	1.1	1.0	8.3	3.5
	128	1.7	1.7	8.5	4.0	2.4	3.5	12.5	6.2
5000	32	0.3	0.5	4.3	1.7	0.6	0.4	4.3	1.8
	64	0.2	0.4	6.2	2.3	0.4	0.4	5.1	2.0
	128	0.5	0.5	6.7	2.6	0.2	0.8	7.9	3.0
10000	32	0.2	0.5	3.3	1.3	0.3	0.3	5.3	2.0
	64	0.3	0.5	4.0	1.6	0.4	0.4	5.5	2.1
	128	0.4	0.5	4.4	1.8	0.4	0.3	5.3	2.0

下载: 导出CSV

表 4 不同噪声条件下FF-APUF可靠性和攻击预测率

CRP个数	激励位数	噪声系数α
CRP个数	激励位数	0	0.0125	0.025	0.050	0.100	0.150	0.200
可靠性(%)	32	100.00	99.67	99.20	98.85	96.38	95.40	93.42
	64	100.00	99.68	99.16	98.33	96.14	95.57	93.39
	128	100.00	99.58	99.21	98.23	96.20	95.14	93.28
预测率(%)	32	99.94	99.57	98.91	98.57	96.11	94.28	93.31
	64	99.86	99.41	98.09	98.08	95.68	95.54	93.12
	128	99.80	99.59	99.10	98.27	95.23	95.06	92.62

下载: 导出CSV

参考文献(18)

[1]	LI Gang, WANG Pengjun, MA Xuejiao, et al. A multimode configurable physically unclonable function with bit-instability-screening and power-gating strategies[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2021, 29(1): 100–111. doi: 10.1109/TVLSI.2020.3030945
[2]	YAN Wei, TEHRANIPOOR F, and CHANDY J A. PUF-based fuzzy authentication without error correcting codes[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, 36(9): 1445–1457. doi: 10.1109/TCAD.2016.2638445
[3]	USMANI M A, KESHAVARZ S, MATTHEWS E, et al. Efficient PUF-based key generation in FPGAs using per-device configuration[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2019, 27(2): 364–375. doi: 10.1109/TVLSI.2018.2877438
[4]	汪鹏君, 李乐薇, 郑雁公, 等. 基于气敏传感器的高稳态物理不可克隆函数发生器[J]. 电子与信息学报, 2021, 43(6): 1596–1602. doi: 10.11999/JEIT201104 WANG Pengjun, LI Lewei, ZHENG Yangong, et al. High steady-state physical unclonable function generator based on gas sensors[J]. Journal of Electronics &Information Technology, 2021, 43(6): 1596–1602. doi: 10.11999/JEIT201104
[5]	徐金甫, 吴缙, 李军伟, 等. 基于敏感度混淆机制的控制型物理不可克隆函数研究[J]. 电子与信息学报, 2019, 41(7): 1601–1609. doi: 10.11999/JEIT180775 XU Jinfu, WU Jin, LI Junwei, et al. Controlled physical unclonable function research based on sensitivity confusion mechanism[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1601–1609. doi: 10.11999/JEIT180775
[6]	LIM D. Extracting secret keys from integrated circuits[D]. [Ph. D. dissertation], Massachusetts Institute of Technology, 2004.
[7]	RÜHRMAIR U, SÖLTER J, SEHNKE F, et al. PUF modeling attacks on simulated and silicon data[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(11): 1876–1891. doi: 10.1109/TIFS.2013.2279798
[8]	SUH G E and DEVADAS S. Physical unclonable functions for device authentication and secret key generation[C]. The 44th ACM/IEEE Design Automation Conference, San Diego, USA, 2007: 9–14. doi: 10.1145/1278480.1278484.
[9]	MAITI A and SCHAUMONT P. Improving the quality of a physical unclonable function using configurable ring oscillators[C]. 2009 International Conference on Field Programmable Logic and Applications, Prague, Czech Republic, 2009: 703–707. doi: 10.1109/FPL.2009.5272361.
[10]	SAHOO D P, NGUYEN P H, MUKHOPADHYAY D, et al. A case of lightweight PUF constructions: Cryptanalysis and machine learning attacks[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2015, 34(8): 1334–1343. doi: 10.1109/TCAD.2015.2448677
[11]	NGUYEN P H, SAHOO D P, JIN Chenglu, et al. The interpose PUF: Secure PUF design against state-of-the-art machine learning attacks[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019, 2019(4): 243–290. doi: 10.13154/tches.v2019.i4.243-290
[12]	SAHOO D P, MUKHOPADHYAY D, CHAKRABORTY R S, et al. A multiplexer-based arbiter PUF composition with enhanced reliability and security[J]. IEEE Transactions on Computers, 2018, 67(3): 403–417. doi: 10.1109/TC.2017.2749226
[13]	GU Chongyan, LIU Weiqiang, CUI Yijun, et al. A Flip-Flop based Arbiter Physical Unclonable Function (APUF) design with high entropy and uniqueness for FPGA implementation[J]. IEEE Transactions on Emerging Topics in Computing, To be published. doi: 10.1109/TETC.2019.2935465.
[14]	AWANO H, IIZUKA T, and IKEDA M. PUFNet: A deep neural network based modeling attack for physically unclonable function[C]. 2019 IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 2019: 1–4. doi: 10.1109/ISCAS.2019.8702431.
[15]	SANTIKELLUR P and CHAKRABORTY R S. A computationally efficient tensor regression network-based modeling attack on XOR arbiter PUF and its variants[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2021, 40(6): 1197–1206. doi: 10.1109/TCAD.2020.3032624
[16]	SHI Junye, LU Yang, and ZHANG Jiliang. Approximation attacks on strong PUFs[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020, 39(10): 2138–2151. doi: 10.1109/TCAD.2019.2962115
[17]	CHATTERJEE D, MUKHOPADHYAY D, and HAZRA A. Interpose PUF can be PAC learned[OL]. https://www.researchgate.net/publication/343524875_Interpose_PUF_can_be_PAC_Learned?channel=doi&linkId=5f2e86d5458515b7290d567f&showFulltext=true. 2020.
[18]	CHAKRABORTY R S, JELDI R R, SAHA I, et al. Binary decision diagram assisted modeling of FPGA-based physically unclonable function by genetic programming[J]. IEEE Transactions on Computers, 2017, 66(6): 971–981. doi: 10.1109/TC.2016.2603498