Objective Reduction Algorithm Based on Decomposition and Hyperplane Approximation for Evolutionary Many-Objective Optimization
-
摘要: 目标降维是研究超多目标优化问题的一个重要方向,它通过恰当的算法设计,能够剔除一些对求解优化问题冗余的目标,达到极大简化优化问题的效果。在超多目标优化降维问题中,前沿界面呈现非线性的情形是最普遍也是最难处理的降维问题。该文提出一种基于分解和超平面拟合的算法(DHA)来处理这类目标降维问题,通过对进化过程中种群的有效分解,使得在几何上非线性分布的非劣解集近似分解为多个近似线性分布的子集,再用系数是稀疏的超平面结合一些扰动项去拟合这些非劣解子集,最后根据该超平面提取出原问题的本质目标集,达到去除冗余目标的效果。为了检验提出算法的有效性,采用DTLZ5(I, m), WFG3(I, m)和MAOP(I, m)作为测试问题集,与代表当今水平的著名算法进行比较。计算机仿真结果表明该文提出的算法无论前沿界面是线性或非线性的情形都具有优异的性能。Abstract: Objective reduction is an important research direction in many-objective optimization. Through proper algorithm design, it can eliminate some redundant objectives to achieve the effect of greatly simplifying an optimization problem. Among the many-objective optimization problems with redundant objectives, the problems with nonlinear Pareto-Front are the most common and most difficult to tackle. In this paper, an algorithm based on Decomposition and Hyperplane Approximation (DHA) is proposed to deal with objective reduction problems with nonlinear Pareto-Front. The proposed algorithm decomposes a population with nonlinear geometric distribution into several subsets with approximate linear distribution in the process of evolution, and uses a hyperplane with sparse coefficients combined with some perturbation terms to fit these subsets, and then it extractes an essential objective set of original problem based on the coefficients of the fitting hyperplane. In order to test the performance of the proposed algorithm, this study compares it with some state-of-the-art algorithms in the benchmark DTLZ5(I, m), WFG3(I, m) and MAOP(I, m). The experimental results show that the proposed algorithm has good performance both in the problems with linear and nonlinear Pareto-Front.
-
表 1 在线的进化目标降维算法DHA
输入:多目标优化问题MOP,种群规模$ N $,迭代代数$ G $,PF子集个数$ K $,参数$ \lambda $。 输出:多目标子集${\boldsymbol{F}}''$。 主程序: 步骤1 初试化:初始种群$ {P_0} $,令当前种群$ {P_c}{\text{ = }}{P_0} $,初始目标集${\boldsymbol{F}} = \left\{ { {f_1},\;{f_2},\; \cdots ,\;{f_m} } \right\}$。 步骤2 采用MOEA对多目标优化问题运行$ G $代(本文采用基于分解的算法MOEA/D-M2M[17]来获取解集),记运行$ G $代后的种群为$ P' $,将
$ P' $对应在目标空间的取值记为目标矩阵$ {\boldsymbol{A}} $;更新当前种群$ {P_c}{\text{ = }}P' $。根据$ P' $的取值范围调整MOEA/D-M2M的权重向量。步骤3 令$ \sigma $=$ {\text{10}} \times \lambda $,将$ {\boldsymbol{A}} $,$ \lambda $,$ K $和$ \sigma $作为输入,调用离线的DHA(表2)进行降维,将提取的目标集合记为$ {\boldsymbol{F'}} $。 步骤4 将$ {\boldsymbol{F'}} $中的目标作为新的多目标优化问题,以${P_c}$为初始种群,调用进化算法进行求解。将运行$ G $代后种群记为$ P'' $,用$ P'' $组成的目
标矩阵更新$ {\boldsymbol{A}} $,更新当前种群$ {P_c}{\text{ = }}P'' $。步骤5 对$ {\boldsymbol{A}} $调用离线的DHA(表2)进行降维,将提取的多目标子集记为${\boldsymbol{F}}''$,若${\boldsymbol{F}}''$的目标个数少于${\boldsymbol{F}}'$,则返回步骤4,否则输出多目标子
集${\boldsymbol{F}}''$并结束。表 2 离线的目标降维算法DHA
输入:进化$ G $代后的目标矩阵${\boldsymbol{A}}$,参数$ \lambda $,子种群数$ K $。 输出:多目标子集${\boldsymbol{F}}'$。 主程序: 步骤1 根据3.2节给出的分解方法对$ A $进行分解,得到$ K $个子种群对应的目标矩阵,记为${{\boldsymbol{H}}_i}$,$ i = 1,\;2,\; \cdots ,\;K $,再对每个子集独立归一
化(将各个子种群视为整体)处理。步骤2 根据所给的参数$ \lambda $和步骤1得到的$ K $个目标矩阵${{\boldsymbol{H}}_i}$,($ i = 1,\;2,\; \cdots ,\;K $),求解凸优化问题式(3)得到解向量${\boldsymbol{w}}$(本文实验时使用
cvx凸优化工具包,在软件MATLAB中进行求解)。步骤3 令${\boldsymbol{w}} = {\boldsymbol{w}}/{\text{max} }\left( {\boldsymbol{w}} \right)$,对于$ i = 1,\;2,\; \cdots ,\;m $,若$ {w_i} > 0.1 $,则${\boldsymbol{F}}' \cup \left\{ { {f_i} } \right\}$。输出${\boldsymbol{F}}'$。 表 3 降维算法参数表
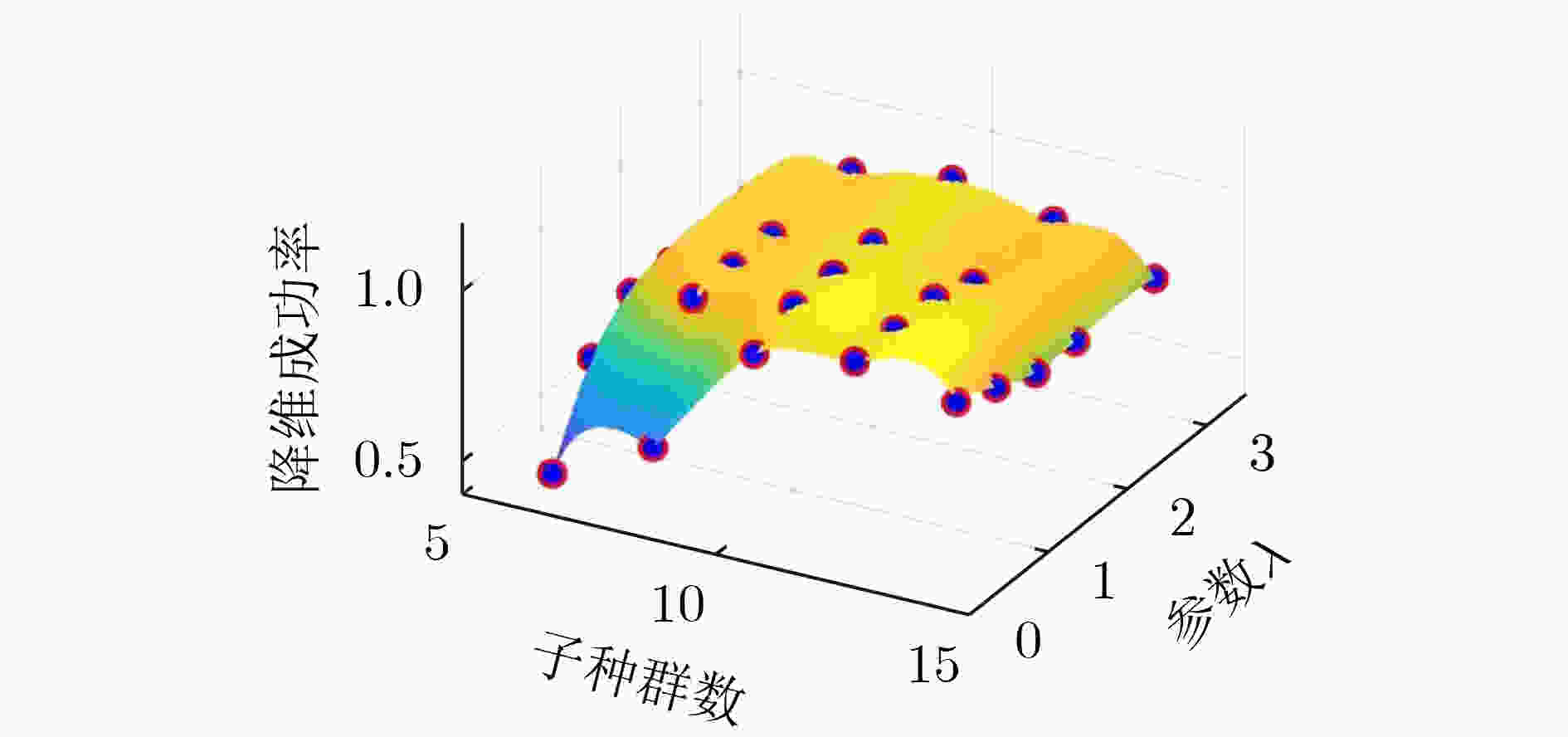
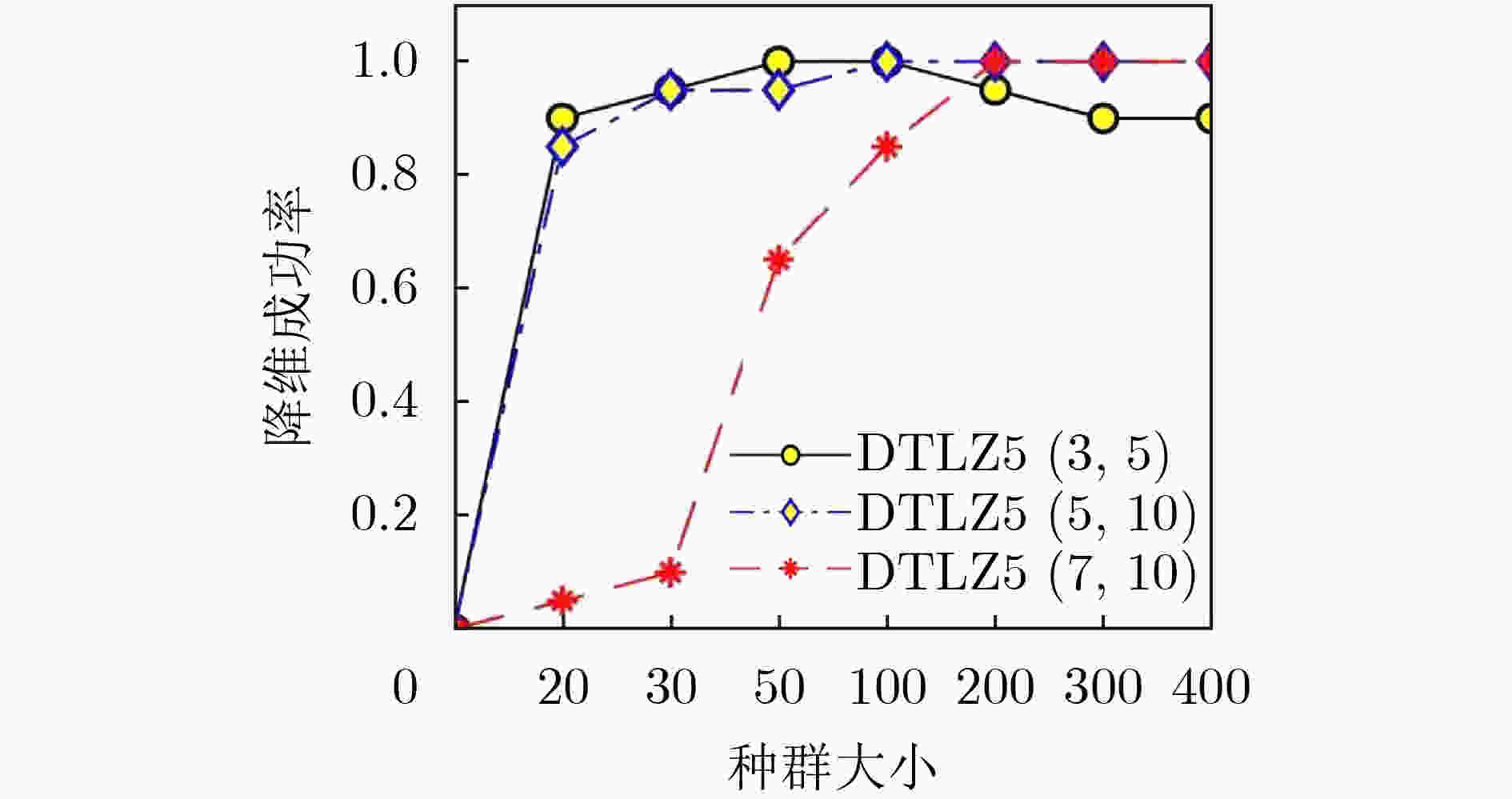
表 4 各算法在DTLZ5(I, m), WFG(I, m), MAOP(I, m)问题上的降维成功率
测试问题 LPCA NLMVUPCA PCSEA greedy $ \delta $-MOSS LHA NLHA DHA DTLZ5(2, 5) 1.000 1.000 1.000 0.600 1.000 1.000 1.000 DTLZ5(5, 10) 1.000 1.000 1.000 1.000 1.000 1.000 1.000 DTLZ5(7, 10) 1.000 0.750 0.000 1.000 0.950 1.000 1.000 DTLZ5(2, 20) 1.000 1.000 1.000 0.800 1.000 1.000 1.000 DTLZ5(5, 20) 1.000 1.000 1.000 1.000 0.950 0.950 1.000 DTLZ5(7, 20) 1.000 0.650 0.000 1.000 0.900 0.950 0.900 DTLZ5(2, 50) 0.000 1.000 1.000 0.750 0.000 0.350 0.800 WFG3(2, 15) 1.000 1.000 1.000 1.000 0.950 0.950 0.850 WFG3(5, 15) 1.000 0.600 1.000 1.000 1.000 1.000 1.000 WFG3(7, 15) 1.000 0.050 0.000 0.750 1.000 1.000 1.000 WFG3(2, 20) 1.000 1.000 1.000 1.000 0.400 0.450 0.850 WFG3(5, 20) 1.000 0.700 1.000 1.000 0.800 0.800 0.950 WFG3(7, 20) 1.000 0.000 0.000 0.850 0.950 0.950 1.000 WFG3(2, 25) 0.000 1.000 1.000 1.000 0.600 0.600 0.700 WFG3(5, 25) 1.000 0.700 1.000 1.000 0.850 0.900 0.600 WFG3(7, 25) 1.000 0.000 0.000 0.950 0.900 0.900 1.000 MAOP1(3, 5) 0.000 1.000 1.000 0.850 1.000 1.000 1.000 MAOP2(3, 5) 0.000 0.000 1.000 0.450 1.000 1.000 1.000 MAOP3(4, 10) 0.000 0.350 0.950 0.950 1.000 1.000 1.000 MAOP4(4, 10) 0.000 0.000 0.000 0.850 0.100 0.100 0.400 MAOP5(6, 10) 0.000 0.000 0.000 0.900 0.500 1.000 1.000 MAOP6(6, 10) 0.000 0.000 0.000 0.900 0.000 0.300 0.900 MAOP7(5, 15) 0.000 0.000 0.000 0.900 0.900 1.000 1.000 MAOP8(5, 15) 0.000 0.000 0.000 0.950 0.000 0.700 0.850 表 5 各算法在DTLZ5(I, m)、WFG(I, m),MAOP(I, m)问题上的的平均
$ {{\boldsymbol{\sigma}} ^ * } $ 值测试问题 LPCA NLMVUPCA PCSEA greedy $ \delta $-MOSS LHA NLHA DHA DTLZ5(2, 5) 1.000 1.000 1.000 0.850 1.000 1.000 1.000 DTLZ5(5, 10) 1.000 1.000 1.000 1.000 1.000 1.000 1.000 DTLZ5(7, 10) 1.000 0.750 0.000 1.000 0.950 1.000 1.000 DTLZ5(2, 20) 1.000 1.000 1.000 0.989 1.000 1.000 1.000 DTLZ5(5, 20) 1.000 1.000 1.000 1.000 0.997 0.997 1.000 DTLZ5(7, 20) 1.000 0.650 0.000 1.000 0.900 0.996 0.986 DTLZ5(2, 50) 0.000 1.000 1.000 0.994 0.955 0.972 0.994 WFG3(2, 15) 1.000 1.000 1.000 1.000 0.996 0.996 0.985 WFG3(5, 15) 1.000 0.600 1.000 1.000 1.000 1.000 1.000 WFG3(7, 15) 1.000 0.050 0.000 0.750 1.000 1.000 1.000 WFG3(2, 20) 1.000 1.000 1.000 1.000 0.967 0.969 0.992 WFG3(5, 20) 1.000 0.700 1.000 1.000 0.987 0.987 0.997 WFG3(7, 20) 1.000 0.000 0.000 0.850 0.996 0.996 1.000 WFG3(2, 25) 0.000 1.000 1.000 1.000 0.980 0.980 0.987 WFG3(5, 25) 1.000 0.700 1.000 1.000 0.993 0.995 0.978 WFG3(7, 25) 1.000 0.000 0.000 0.950 0.994 0.994 1.000 MAOP1(3, 5) 0.000 1.000 1.000 0.925 1.000 1.000 1.000 MAOP2(3, 5) 0.500 0.000 1.000 0.725 1.000 1.000 1.000 MAOP3(4, 10) 0.529 0.650 0.975 0.992 1.000 1.000 1.000 MAOP4(4, 10) 0.015 0.000 0.933 0.975 0.940 0.940 0.960 MAOP5(6, 10) 0.307 0.025 0.500 0.975 0.867 1.000 1.000 MAOP6(6, 10) 0.715 0.096 0.463 0.984 0.956 0.974 0.995 MAOP7(5, 15) 0.152 0.111 0.447 0.990 0.972 1.000 1.000 MAOP8(5, 15) 0.510 0.460 0.658 0.995 0.877 0.969 0.964 表 6 DHA-MOEA/D-M2M与MOEA/D-M2M在各个测试函数独立运行20次的平均IGD值与标准差
算法 DTLZ5(5, 10) DTLZ5(2, 20) DTLZ5(5, 20) MAOP1(3, 5) MAOP3(4, 10) MAOP5(6, 10) MOEA/D-M2M 2.11E-1(1.1E-2) 1.61E-2(1.61E-2) 3.09E-1(2.8E-2) 6.23E-2(4.2E-3) 1.45E-1(5.8E-3) 1.56E-1(5.7E-3) DHA_MOEA/D-M2M 1.74E-1(2.7E-3) 2.10E-3(1.1E-3) 1.74E-1(3.6E-3) 6.36E-2(4.6E-3) 1.17E-1(3.6E-3) 1.32E-1(6.7E-3) -
[1] SAXENA D K, DURO J A, TIWARI A, et al. Objective reduction in many-objective optimization: Linear and nonlinear algorithms[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(1): 77–99. doi: 10.1109/TEVC.2012.2185847 [2] 赵辉, 王天龙, 刘衍舟, 等. 基于分解和支配关系的超多目标进化算法[J]. 电子与信息学报, 2020, 42(8): 1975–1981. doi: 10.11999/JEIT190589ZHAO Hui, WANG Tianlong, LIU Yanzhou, et al. Decomposition and dominance relation based many-objective evolutionary algorithm[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1975–1981. doi: 10.11999/JEIT190589 [3] 刘建昌, 李飞, 王洪海, 等. 进化高维多目标优化算法研究综述[J]. 控制与决策, 2018, 33(5): 879–887. doi: 10.13195/j.kzyjc.2017.1442LIU Jianchang, LI Fei, WANG Honghai, et al. Survey on evolutionary many-objective optimization algorithms[J]. Control and Decision, 2018, 33(5): 879–887. doi: 10.13195/j.kzyjc.2017.1442 [4] YUAN Jiawei, LIU Hailin, GU Fangqing, et al. Investigating the properties of indicators and an evolutionary many-objective algorithm using promising regions[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(1): 75–86. doi: 10.1109/TEVC.2020.2999100 [5] CHEN Lu, WANG Handing, and MA Wenping. Two-stage multi-tasking transform framework for large-scale many-objective optimization problems[J]. Complex & Intelligent Systems, 2021, 7(3): 1499–1513. doi: 10.1007/s40747-021-00273-5 [6] 毕晓君, 王朝. 一种基于角度惩罚距离的高维多目标进化算法[J]. 电子与信息学报, 2018, 40(2): 314–322. doi: 10.11999/JEIT170454BI Xiaojun and WANG Chao. A many-objective evolutionary algorithm based on angle penalized distance[J]. Journal of Electronics &Information Technology, 2018, 40(2): 314–322. doi: 10.11999/JEIT170454 [7] MA Lianbo, HUANG Min, YANG Shengxiang, et al. An adaptive localized decision variable analysis approach to large-scale multiobjective and many-objective optimization[J]. IEEE Transactions on Cybernetics, 2022, 52(7): 6684–6696. [8] SINGH H K, ISAACS A, and RAY T. A pareto corner search evolutionary algorithm and dimensionality reduction in many-objective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(4): 539–556. doi: 10.1109/TEVC.2010.2093579 [9] CHEUNG Y M, GU Fangqing, and LIU Hailin. Objective extraction for many-objective optimization problems: Algorithm and test problems[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 755–772. doi: 10.1109/TEVC.2016.2519758 [10] BROCKHOFF D and ZITZLER E. Objective reduction in evolutionary multiobjective optimization: Theory and applications[J]. Evolutionary Computation, 2009, 17(2): 135–166. doi: 10.1162/evco.2009.17.2.135 [11] YUAN Yuan, ONG Y S, GUPTA A, et al. Objective reduction in many-objective optimization: Evolutionary multiobjective approaches and comprehensive analysis[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(2): 189–210. doi: 10.1109/TEVC.2017.2672668 [12] QIN Yingjie, ZHENG Jiehui, LI Zhigang, et al. Reduction of non-linear many objectives for coordinated operation of integrated energy systems[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105657. doi: 10.1016/j.ijepes.2019.105657 [13] 陈小红, 李霞, 王娜. 高维多目标优化中基于稀疏特征选择的目标降维方法[J]. 电子学报, 2015, 43(7): 1300–1307. doi: 10.3969/j.issn.0372-2112.2015.07.008CHEN Xiaohong, LI Xia, and WANG Na. Objective reduction with sparse feature selection for many objective optimization problem[J]. Acta Electronica Sinica, 2015, 43(7): 1300–1307. doi: 10.3969/j.issn.0372-2112.2015.07.008 [14] SAXENA D K and DEB K. Non-linear dimensionality reduction procedures for certain large-dimensional multi-objective optimization problems: Employing correntropy and a novel maximum variance unfolding[C]. The 4th International Conference on Evolutionary Multi-Criterion Optimization, Matsushima, Japan, 2007: 772–787. [15] LI Yifan, LIU Hailin, and GOODMAN E D. Hyperplane-approximation-based method for many-objective optimization problems with redundant objectives[J]. Evolutionary Computation, 2019, 27(2): 313–344. doi: 10.1162/evco_a_00223 [16] LIU Hailin, CHEN Lei, ZHANG Qingfu, et al. An evolutionary many-objective optimisation algorithm with adaptive region decomposition[C]. 2016 IEEE Congress on Evolutionary Computation, Vancouver, Canada, 2016: 4763–4769. [17] LIU Hailin, GU Fangqing, and ZHANG Qingfu. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 450–455. doi: 10.1109/TEVC.2013.2281533 [18] BOSMAN P A N and THIERENS D. The balance between proximity and diversity in multiobjective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 174–188. doi: 10.1109/TEVC.2003.810761 -





 下载:
下载:





 下载:
下载:
