基于塔域的通用循环移位掩码设计方法

严迎建; 汪晶; 刘燕江

doi:10.11999/JEIT210588

基于塔域的通用循环移位掩码设计方法

doi: 10.11999/JEIT210588

中国人民解放军战略支援部队信息工程大学郑州 450001

详细信息

作者简介:
严迎建：男，1973年生，教授，研究方向为安全专用芯片设计技术、侧信道分析等

汪晶：女，1997年生，硕士生，研究领域为安全专用芯片设计技术、侧信道分析

刘燕江：男，1990年生，博士后，研究领域为安全专用芯片设计技术、侧信道分析和硬件木马检测等

通讯作者:
汪晶　cristal_97@163.com

中图分类号: TN918.4; TP309.7
计量
- 文章访问数: 872
- HTML全文浏览量: 528
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-16
- 修回日期: 2021-07-15
- 网络出版日期: 2021-08-18
- 刊出日期: 2021-09-16

Design Method of Generic Cyclic Shift Mask Based on Tower Field

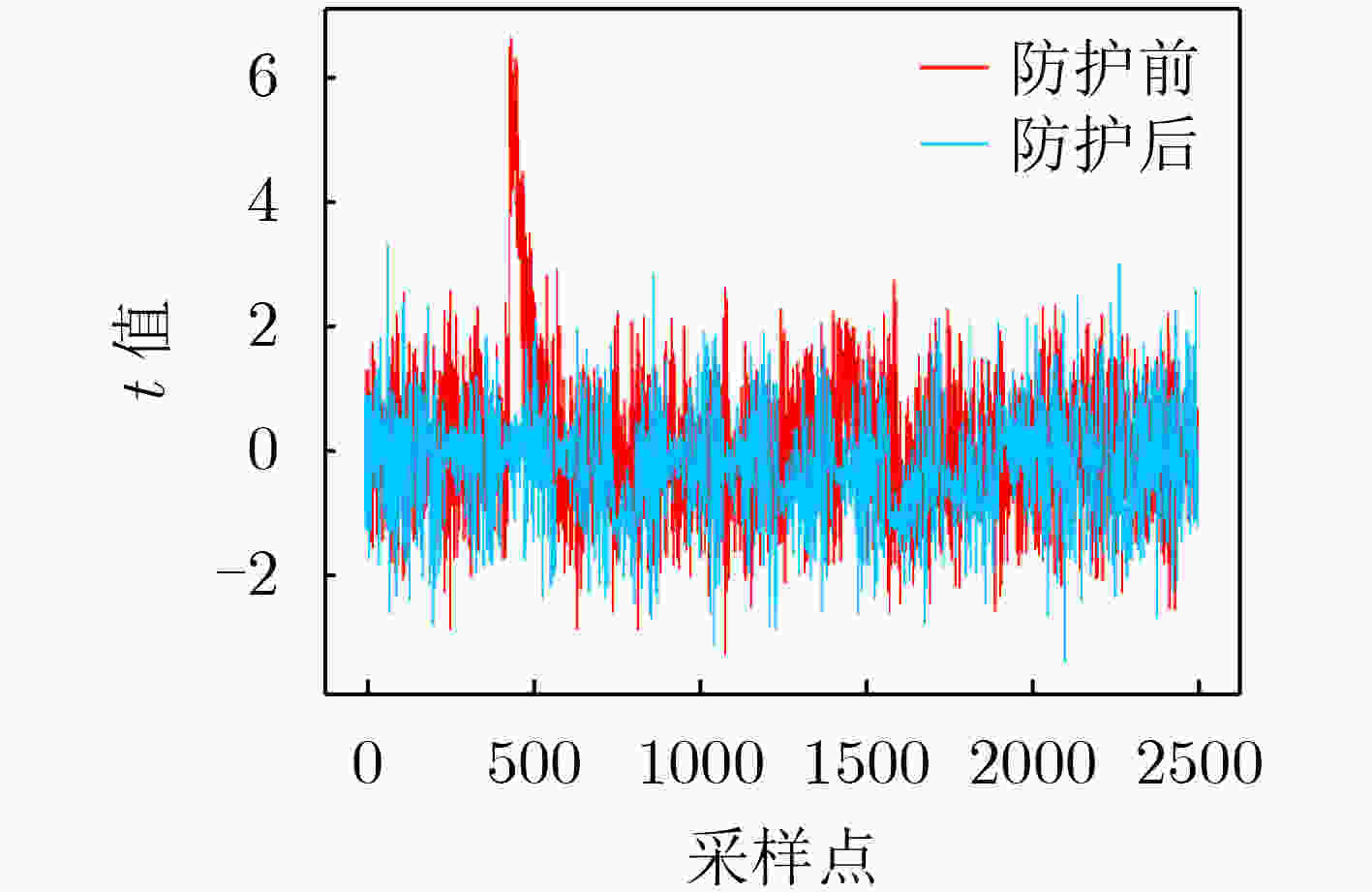
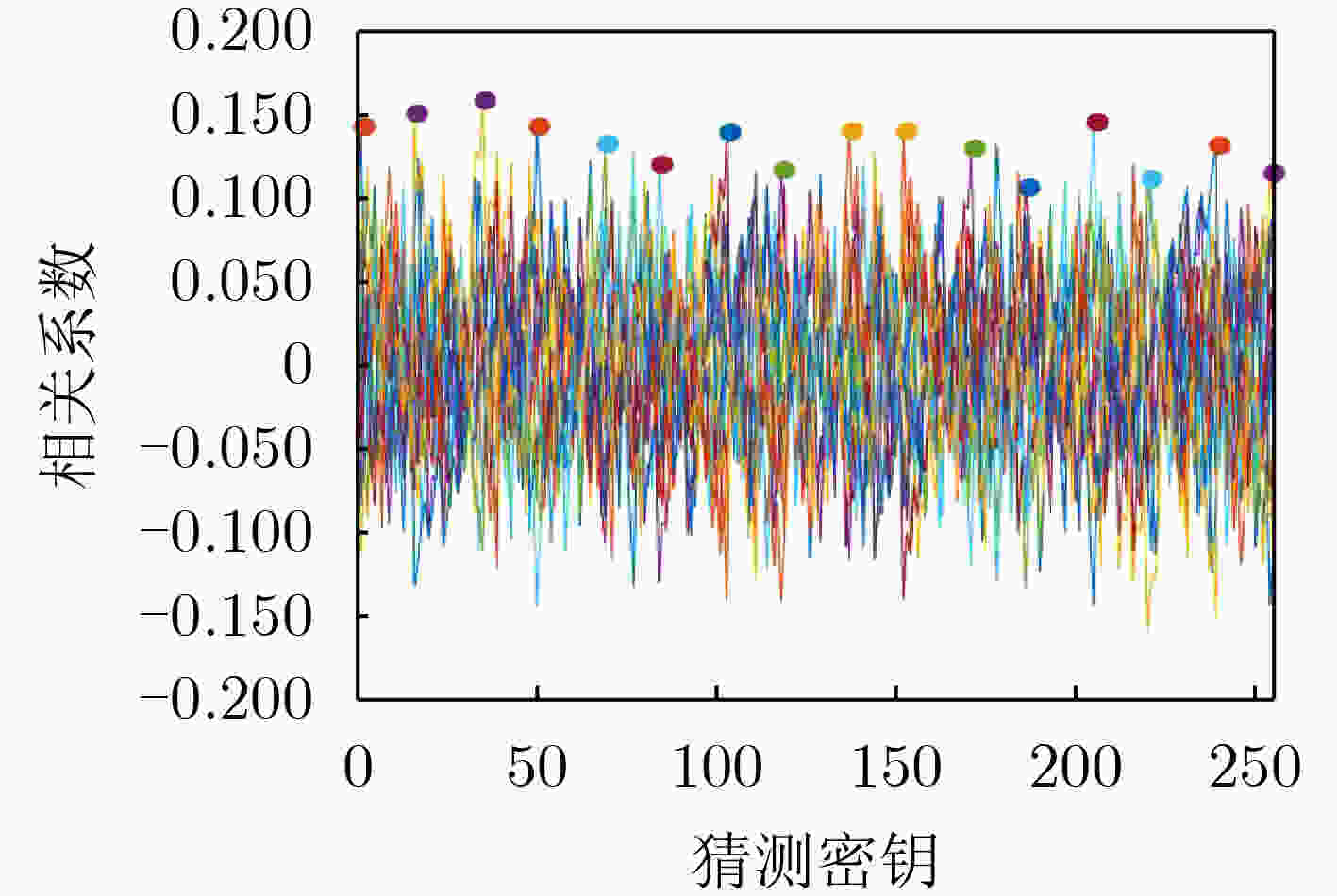
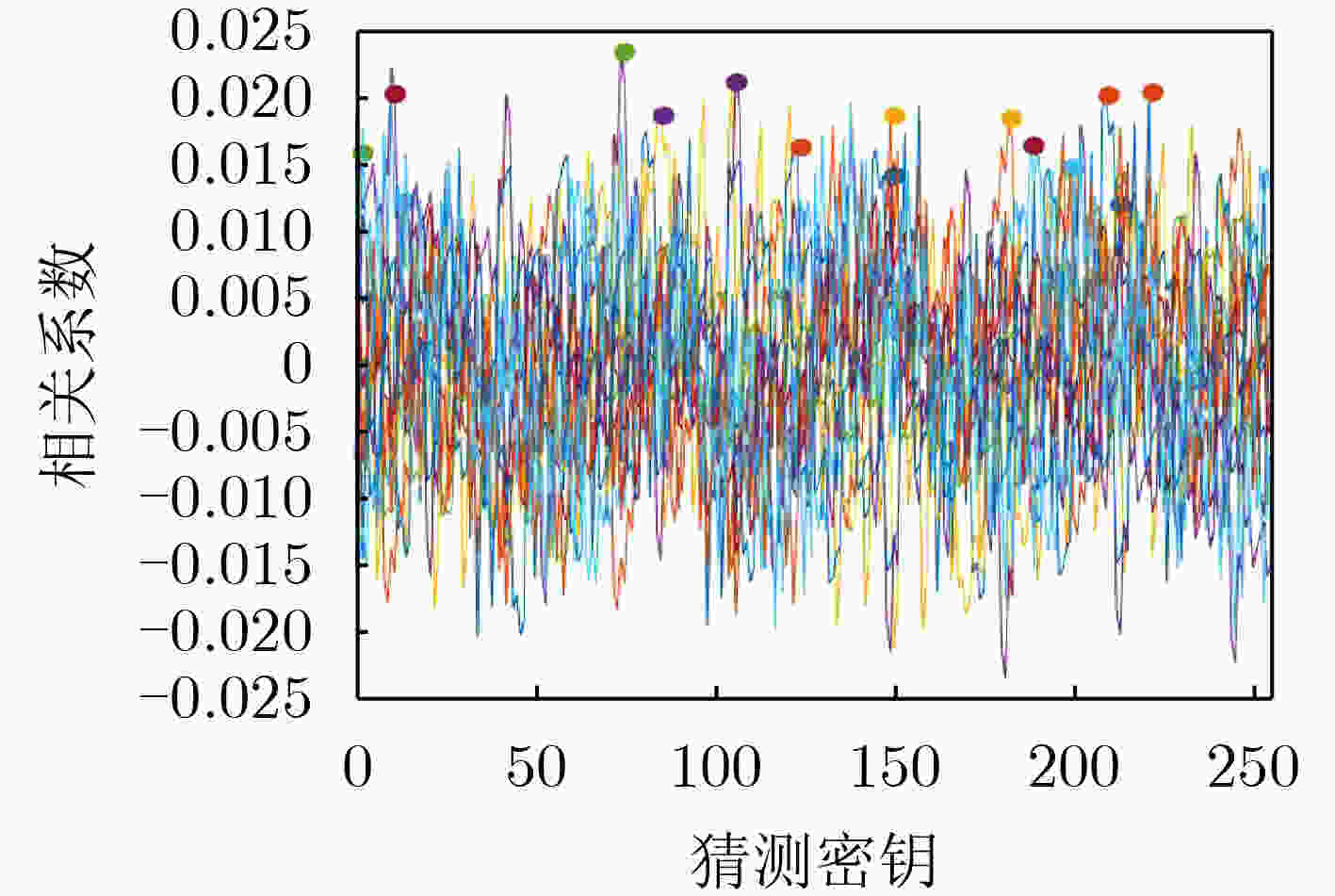
Information Engineering University, People’s Liberation Army Strategic Support Force, Zhengzhou 450001, China

摘要

摘要: 该文分析了塔域的运算特性，提出了基于塔域分解的非线性变换实现方法，设计了求逆运算的随机掩码方案，利用循环移位对随机掩码进行移位变换，形成了基于塔域的循环移位随机掩码方案，实现了所有中间值的随机化隐藏，提高了算法的抗能量攻击能力。该文在高级加密标准(AES)算法上进行验证，利用T-test和相关性分析对掩码方案进行安全性评估。该掩码方案无明显信息泄露点，可有效抵抗相关性攻击，另外较现有文献的掩码方案，资源开销更小，通用性更好。
- 能量攻击 /
- 掩码 /
- 复合域 /
- 分组密码
Abstract: The operation characteristics of the tower field is analyzed, a nonlinear transformation realization method based on the tower domain is proposed. A random mask schedule for the inversion operation is designed, and cyclic shift is used in the randomization of mask, forming cyclic shift random mask scheme based on the tower domain, realizing the randomized hiding of all intermediate values and improving the ability of the algorithm to resist power attacks. The method proposed is verified on the Advanced Encryption Standard (AES) algorithm with the use of T-test and correlation analysis to evaluate the security of the masking scheme. There is no obvious information leakage points in the schedule, proving the ability to effectively resist correlation attacks. In addition, compared with the mask schedule in existing reference, the mask schedule proposed in this paper has less resource overhead and better generality.
- Power attack /
- Mask /
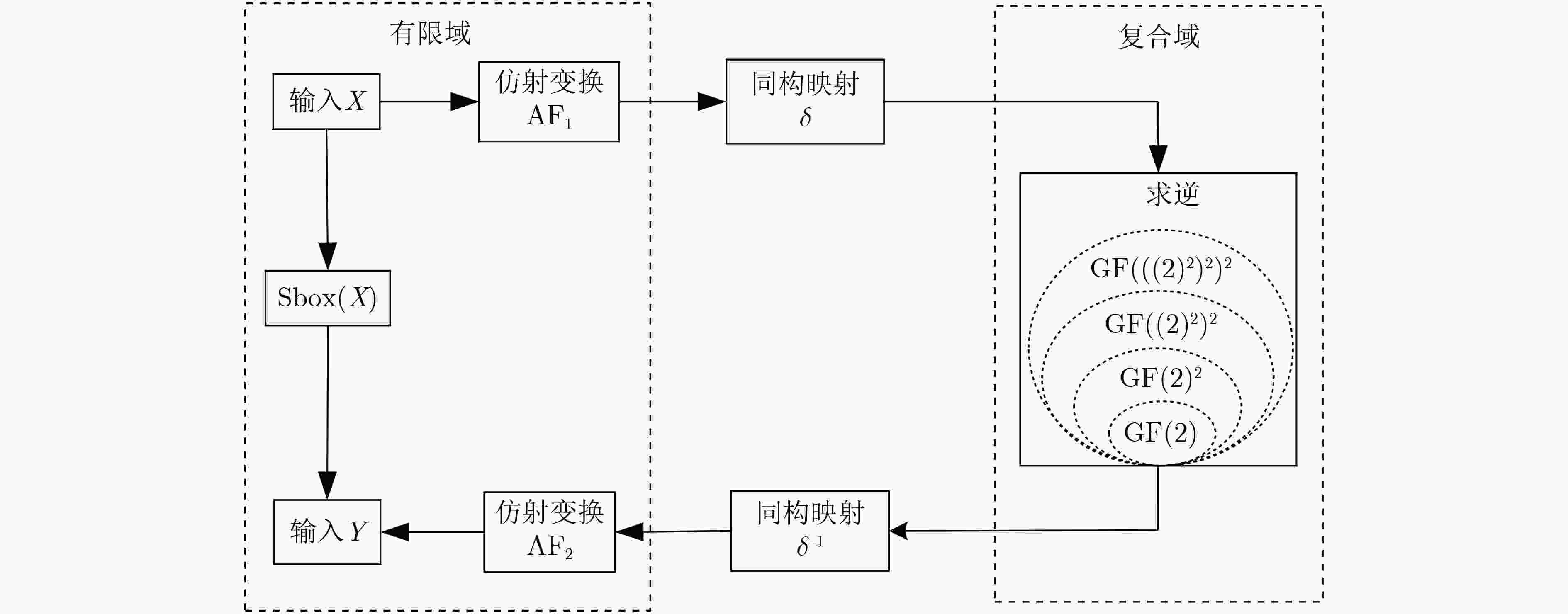
- Composite field /
- Block cipher

HTML全文

图 1 基于塔域的S盒运算结构

下载: 全尺寸图片幻灯片

图 2 GF(((2)²)²)²上元素乘法逆计算结构图

下载: 全尺寸图片幻灯片

图 3 基于塔域AES加掩S盒硬件实现

下载: 全尺寸图片幻灯片

图 4 基于塔域的AES-128加掩算法

下载: 全尺寸图片幻灯片

图 5 基于塔域的循环移位加掩AES功能仿真图

下载: 全尺寸图片幻灯片

图 6 波形采集设备连接图

下载: 全尺寸图片幻灯片

图 7 有无防护AES功耗轨迹t检验结果

下载: 全尺寸图片幻灯片

图 8 无防护AES相关能量攻击结果

下载: 全尺寸图片幻灯片

图 9 本文所提防护方案AES相关能量攻击结果

下载: 全尺寸图片幻灯片

表 1 加掩S盒计算算法

输入：m,n,x
输出：MSB
(1)　　for i=0 to 255 do
(2)　　${\rm{MSB}}(x \oplus m) = {\rm{SB}}(x) \oplus n$
(3)　　end for
(4)　　Return MSB

下载: 导出CSV

表 2 加法链计算算法

输入：x
输出：x²⁵⁴
(1)	z←x²	[z=x²]
(2)	y←zx	[y=x²x=x³]
(3)	w←y⁴	[w=(x³)⁴=x¹²]
(4)	y←yw	[w=x³x¹²=x¹⁵]
(5)	y←y¹⁶	[w=(x¹⁵)¹⁶=x²⁴⁰]
(6)	y←yw	[w=x²⁴⁰x¹²=x²⁵²]
(7)	y←yz	[w=x²⁵²x²=x²⁵⁴]

下载: 导出CSV

表 3 基于塔域的循环移位掩码加密算法

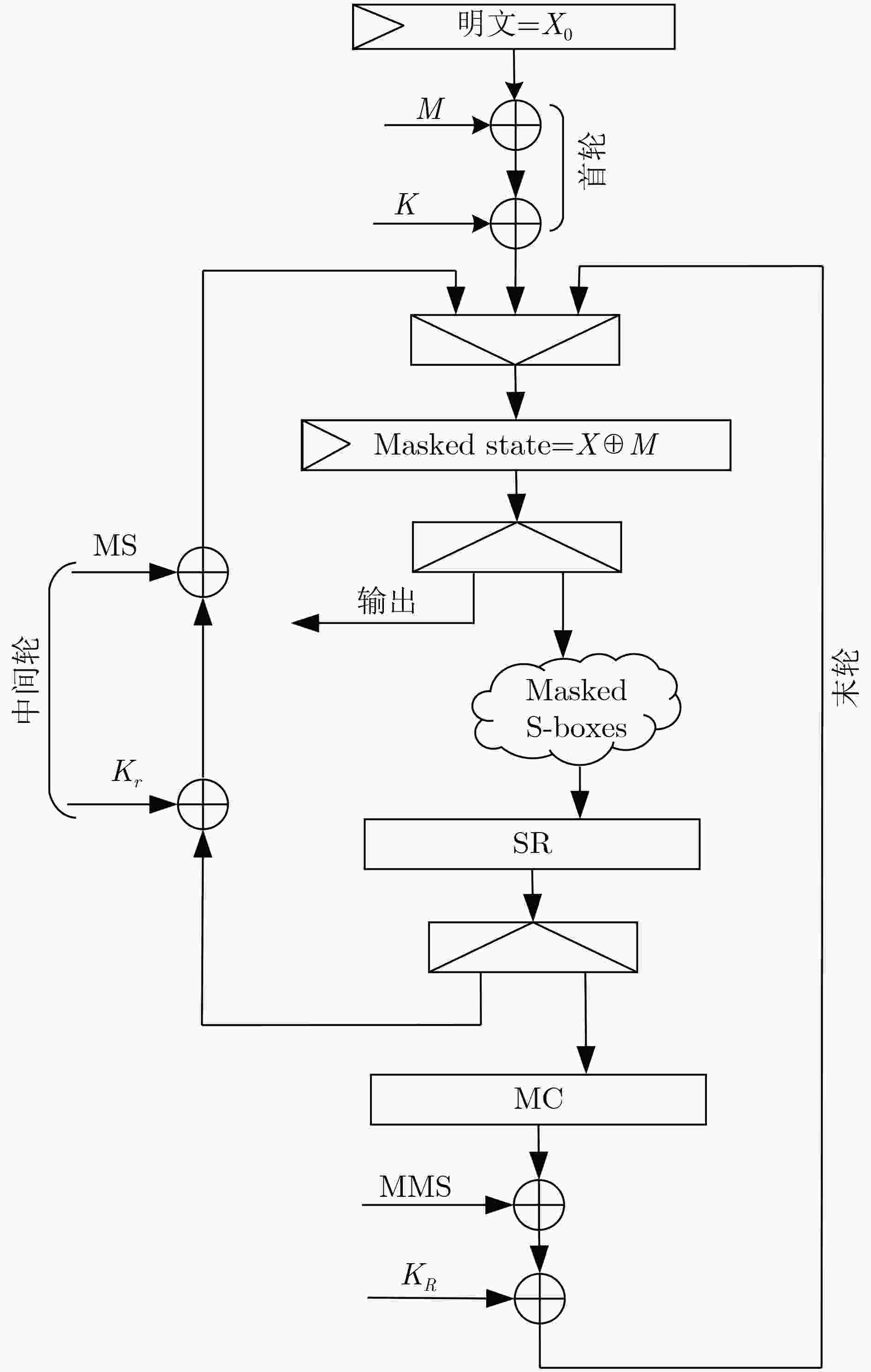
输入：明文X₀，密钥K
输出：密文$ {X}_{R+1}^{{'}{'}} $
(1)　　计算第1轮的输入数据$ {X}_{1}^{{'}} $,
${X'_1} = {X_0} \oplus {K_0} \oplus M$
(2)　　计算轮函数的输出
for r=1 to R–1, 　　　　 $ \begin{array}{l} {{X''}_{r + 1}} = P(S{_{(M,N)}}({{X'}_r})) \oplus {K_r} \\ {{X'}_{r + 1}} = {{X''}_{r + 1}} \oplus ({\tau _{{c_r} + 1}}(M) \oplus P({\tau _{{c_r}}}(N))) \\ {c_{r + 1}} = ({c_r} + 1)\boldsymbolod t \end{array} $
(3)　　计算密文$ {X}_{R+1}^{{'}{'}} $ 　　　　 $ \begin{array}{l} {{X''}_{R + 1}} = S{_{(M,N)}}({{X'}_R}) \oplus {K_R} \\ {{X'}_{R + 1}} = {{X''}_{R + 1}} \oplus {\tau _{{c_{R + 1}}}}(N) \end{array} $

下载: 导出CSV

表 4 不同方案总综合结果比较

方案	LUT	FF	BUFG
无防护AES	1245(303600)	609(607200)	1(32)
RSM方案^[9]	10620(303600)	737(607200)	1(32)
S盒共用掩码方案^[15]	3897(303600)	737(607200)	1(32)
本文方案	2918(303600)	394(607200)	1(32)

下载: 导出CSV

参考文献(19)

[1]	KOCHER P C, JAFFE J, and JUN B. Differential power analysis[C]. The 19th Annual International Cryptology Conference on Advances in Cryptology, Berlin, Germany, 1999: 388–397.
[2]	BRIER E, CLAVIER C, and OLIVIER F. Correlation power analysis with a leakage model[C]. The 6th International Workshop Cambridge, Cambridge, UK, 2004: 16–29.
[3]	DURVAUX F and STANDAERT F X. From improved leakage detection to the detection of points of interests in leakage traces[C]. The 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 2016: 240–262. doi: 10.1007/978-3-662-49890-3_10.
[4]	TIMON B. Non-proﬁled deep learning-based side-channel attacks with sensitivity analysis[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019, 2019(2): 107–131.
[5]	DELGADO-LOZANO I M, TENA-SÁNCHEZ E, NÚÑEZ J, et al. Projection of dual-rail DPA countermeasures in future FinFET and emerging TFET technologies[J]. ACM Journal on Emerging Technologies in Computing Systems, 2020, 16(3): 1–16. doi: 10.1145/3381857
[6]	黄海, 冯新新, 刘红雨, 等. 基于随机加法链的高级加密标准抗侧信道攻击对策[J]. 电子与信息学报, 2019, 41(2): 348–354. doi: 10.11999/JEIT171211 HUANG Hai, FENG Xinxin, LIU Hongyu, et al. Random addition-chain based countermeasure against side-channel attack for advanced encryption standard[J]. Journal of Electronics &Information Technology, 2019, 41(2): 348–354. doi: 10.11999/JEIT171211
[7]	SHAHMIRZADI A R, BOŽILOV D, and MORADI A. New first-order secure AES performance records[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(2): 304–327.
[8]	王立辉, 闫守礼, 李清. 一种轻量级数据加密标准循环掩码实现方案[J]. 电子与信息学报, 2020, 42(8): 1828–1835. doi: 10.11999/JEIT190870 WANG Lihui, YAN Shouli, and LI Qing. A lightweight implementation scheme of data encryption standard with cyclic mask[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1828–1835. doi: 10.11999/JEIT190870
[9]	NASSAR M, SOUISSI Y, GUILLEY S, et al. RSM: a small and fast countermeasure for AES, secure against 1st and 2nd-order zero-offset SCAs[C]. The 2012 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 2012: 1173–1178. doi: 10.1109/DATE.2012.6176671.
[10]	BHASIN S, DANGER J L, GUILLEY S, et al. A low-entropy first-degree secure provable masking scheme for resource-constrained devices[C]. The Workshop on Embedded Systems Security, Quebec, Canada, 2013: 1–10. doi: 10.1145/2527317.2527324.
[11]	GROSSO V, STANDAERT F X, and PROUFF E. Low Entropy Masking Schemes, Revisited[M]. FRANCILLON A and ROHATGI P. Smart Card Research and Advanced Applications. Cham: Springer, 2013, 8419: 33–43.
[12]	MARTINASEK Z, IGLESIAS F, MALINA L, et al. Crucial pitfall of DPA contest V4.2 implementation[J]. Security and Communication Networks, 2016, 9(18): 6094–6110. doi: 10.1002/sec.1760
[13]	徐佩, 傅鹂. 防止差分功耗分析攻击的软件掩码方案[J]. 计算机应用研究, 2016, 33(1): 245–248. doi: 10.3969/j.issn.1001-3695.2016.01.057 XU Pei and FU Li. Software-implemented mask scheme against differential power analysis attack[J]. Application Research of Computers, 2016, 33(1): 245–248. doi: 10.3969/j.issn.1001-3695.2016.01.057
[14]	BHASIN S, BRUNEAU N, DANGER J L, et al. Analysis and improvements of the DPA contest v4 implementation[C]. The 4th International Conference, Pune, India, 2014: 201–218.
[15]	姜久兴, 厚娇, 黄海, 等. 低面积复杂度AES低熵掩码方案的研究[J]. 通信学报, 2019, 40(5): 201–210. JIANG Jiuxing, HOU Jiao, HUANG Hai, et al. Research on area-efficient low-entropy masking scheme for AES[J]. Journal on Communications, 2019, 40(5): 201–210.
[16]	DUC A, FAUST S, and STANDAERT F X. Making masking security proofs concrete (or how to evaluate the security of any leaking device), extended version[J]. Journal of Cryptology, 2019, 32(4): 1263–1297. doi: 10.1007/s00145-018-9277-0
[17]	AHN S and CHOI D. An improved masking scheme for S-Box software implementations[C]. The 16th International Workshop, Jeju Island, South Korea, 2016: 200–212. doi: 10.1007/978-3-319-31875-2_17.
[18]	SINGH A, PRASAD A, and TALWAR Y. Compact and Secure S-Box Implementations of AES—A Review[M]. SOMANI A K, SHEKHAWAT R S, MUNDRA A, et al. Smart Systems and IoT: Innovations in Computing. Singapore: Springer, 2020.
[19]	PROUFF E, RIVAIN M, and BEVAN R. Statistical analysis of second order differential power analysis[J]. IEEE Transactions on Computers, 2009, 58(6): 799–811. doi: 10.1109/tc.2009.15