Dynamic Compensation Based Low-cost Power-analysis Countermeasure for Elliptic Curve Cryptography and Its Hardware Structure
-
摘要: 椭圆曲线密码(ECC)芯片的抗功耗攻击能力往往以电路性能、面积或功耗为代价。该文分析了在椭圆曲线密码 点乘运算中密钥猜测正确与错误时的中间数据汉明距离概率分布差异性,提出一种基于动态汉明距离调控的功耗补偿方法,利用模拟退火算法离线寻找最优的映射矩阵,最终形成椭圆曲线密码硬件电路的等概率映射补偿模型,大大降低了中间数据与功耗的相关性。同时,以该模型为指导设计了低成本的同步功耗补偿电路,在CMOS 40 nm工艺下,防护后的ECC128电路面积增加22.8%。基于Sakura-G开发板开展了测试验证,防护电路的功耗仅增加18.8%,最小泄露轨迹数大于104,抗相关功耗分析能力提升了312倍。该策略在与随机化方法防护能力相当的情况下,不损失电路性能且硬件成本小,适用于高速或资源受限的ECC电路。Abstract: The power-analysis countermeasure for Elliptic Curve Cryptographic (ECC) chips endures large area, power consumption and performance degradation. In this paper, the difference in the probability distribution of the intermediate data Hamming distance is analyzed when the key guess is correct and incorrect in the point multiplication of ECC. A power compensation method based on dynamic Hamming distance control is proposed, which uses the simulated annealing algorithm offline to find the optimal mapping matrix. Finally, a mapping compensation model of equal probability on the elliptic curve cryptographic hardware is formed, which greatly reduces the correlation between intermediate data and power consumption. At the same time, a low-cost synchronous power compensation circuit is designed in the guidance of this model. Under the CMOS 40 nm process, the area of protected ECC128 is only increased by 22.8%. Experiments and tests are carried out on the Sakura-G board. The power overhead is 18.8%, and the number of minimum leakage traces is greater than 104, which is increased by 312 times. This countermeasure is the same as randomization with low cost and no impact on the throughput rate, which is suitable for high-speed or resource-constrained ECC circuits.
-
表 1 Radix-4交错模乘算法
输入:A, B, P, 位宽m
输出:$V = A \cdot B\boldsymbolod P$(1) $V = {b_0} \cdot A$, $U = 2A\boldsymbolod P$, $A = 4A\boldsymbolod P$, $B = B/2$;
(2) For i from 0 to $\left\lceil { {{m} }/2} \right\rceil - 1$
$V = (V + {b_0} \cdot U + {b_1} \cdot A)\boldsymbolod P$, $U = 2A\boldsymbolod P$,
$A = 4A\boldsymbolod P$, $B{\rm{ = }}B/4$;
(3) Return V表 2 参数列表
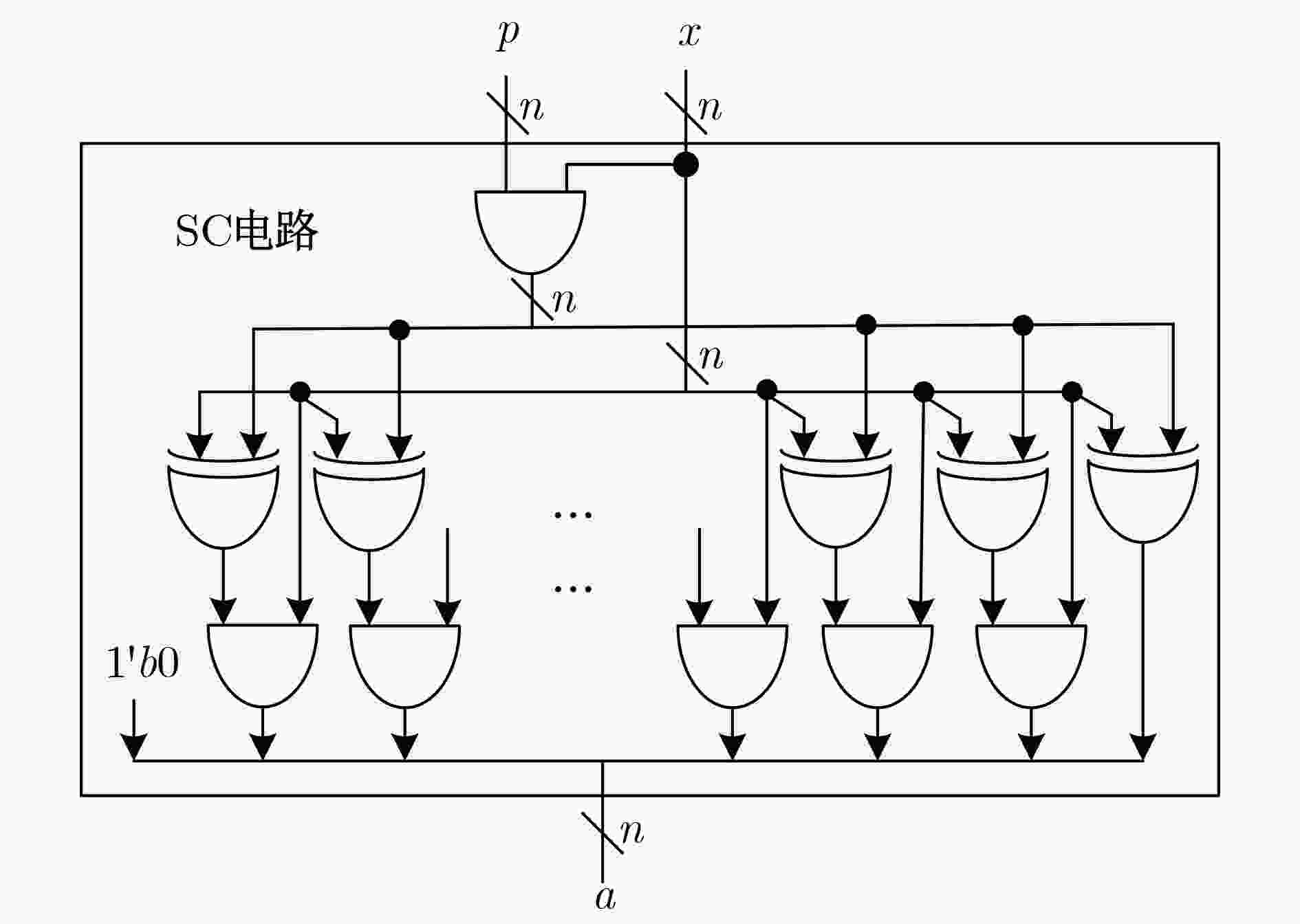
参数 含义 num 模乘除运算中间数据的概率分布函数之差的个数 ${f_{{\rm{wsubr(}}j{\rm{)}}}}$ 第j个密钥猜测错误与正确时的离散概率分布函数之差 mmd ECC硬件实现时,在能量迹上显示出的模乘和模除数量之和 n ECC硬件实现中,中间数据汉明距离的所有可能汉明距离的个数 h 衡量等概率映射时的概率参数,汉明距离以概率2–h被映射为2h个值 M 为一个n行2h的概率矩阵,矩阵中的第x行元素$({m_{x,1} },{m_{x,2} }, ··· ,{m_{x,{2^{{h} } } }})$表示将实际汉明距离x分别以相等的概率2-h映射为${m_{x,1} },{m_{x,2} }, ··· ,{m_{x,{2^{{h} } } }}$ Mi 矩阵的第i列向量 表 3 寻找最优M矩阵的模拟退火算法
输入:代价函数${\rm{cos}}{{\rm{t}}_{{\rm{SUM}}}}$,降温系数α,代价函数阈值${\rm{threshold}}$,矩阵维度n, h;
输出:映射矩阵${\boldsymbol{M'}}$。(1) 初始化${\boldsymbol{M}}$矩阵元素${m_{i,j}} = i$,温度Tmp;
(2) 计算代价函数${\rm{cos}}{{\rm{t}}_{{\rm{old}}}} = {\rm{cos}}{{\rm{t}}_{{\rm{SUM}}}}({\boldsymbol{M}})$;
(3) 生成随机向量${\boldsymbol{r} } = {({r_1},{r_2}, ···, {r_n})_n}$,其中${r_{\rm{i}}}{\rm{ = (}}i{\rm{ - 1) + (}}n{\rm{ - }}i{\rm{ + 1)}} \cdot {\rm{ran}}{{\rm{d}}_i}$, ${\rm{ran}}{{\rm{d}}_i}$为0~1之间的随机数;将矩阵的一列向量更新为
${ {\boldsymbol{M} }_i} = \left\lceil {\boldsymbol{r} } \right\rceil = {({\left\lceil r \right\rceil _1},\left\lceil { {r_2} } \right\rceil , ···, \left\lceil { {r_n} } \right\rceil )^{\rm{T} } }$;
(4) 重复步骤 3,直到矩阵的h个列向量全部被替换,生成新的${{\boldsymbol{M}}_{{\rm{new}}}}$;
(5) 计算新的代价函数${\rm{cos}}{{\rm{t}}_{{\rm{new}}}}$,以及$\delta = {\rm{cos}}{{\rm{t}}_{{\rm{new}}}} - {\rm{cos}}{{\rm{t}}_{{\rm{old}}}}$;
(6) 生成一个0~1的随机数R,若$\delta < 0$,则${\boldsymbol{M}} = {{\boldsymbol{M}}_{{\rm{new}}}}$, ${\rm{cos}}{{\rm{t}}_{{\rm{old}}}}{\rm{ = cos}}{{\rm{t}}_{{\rm{new}}}}$;
否则,若$\exp ({\rm{ - }}\delta /{\rm{Tmp}}) > R$,则${\boldsymbol{M}} = {{\boldsymbol{M}}_{{\rm{new}}}}$, ${\rm{cos}}{{\rm{t}}_{{\rm{old}}}}{\rm{ = cos}}{{\rm{t}}_{{\rm{new}}}}$,并进行降温,令${\rm{Tmp}} = {\rm{Tmp}} \cdot \alpha $;
(7) 若${\rm{cos}}{{\rm{t}}_{{\rm{old}}}}{\rm{ > threshold}}$,则返回步骤 3;
(8) 令${\boldsymbol{M}}$中的元素${m_{i,j}} = {m_{i,j}} - i$,生成${\boldsymbol{M'}}$矩阵并返回。表 4 由
${c_i}$ 输出值推导出的${a_i}$ 真值表${ {{p} }_i}$ ${c_i}$ ${c_{i{\rm{ - }}1}}$ ${a_i}$ ${a'_i}$ 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 1 1 0 1 0 – X 1 0 0 0 0 1 1 0 1 1 1 1 1 0 0 0 1 1 1 0 1 0 1 – X 表 5 防护前后代价与性能对比
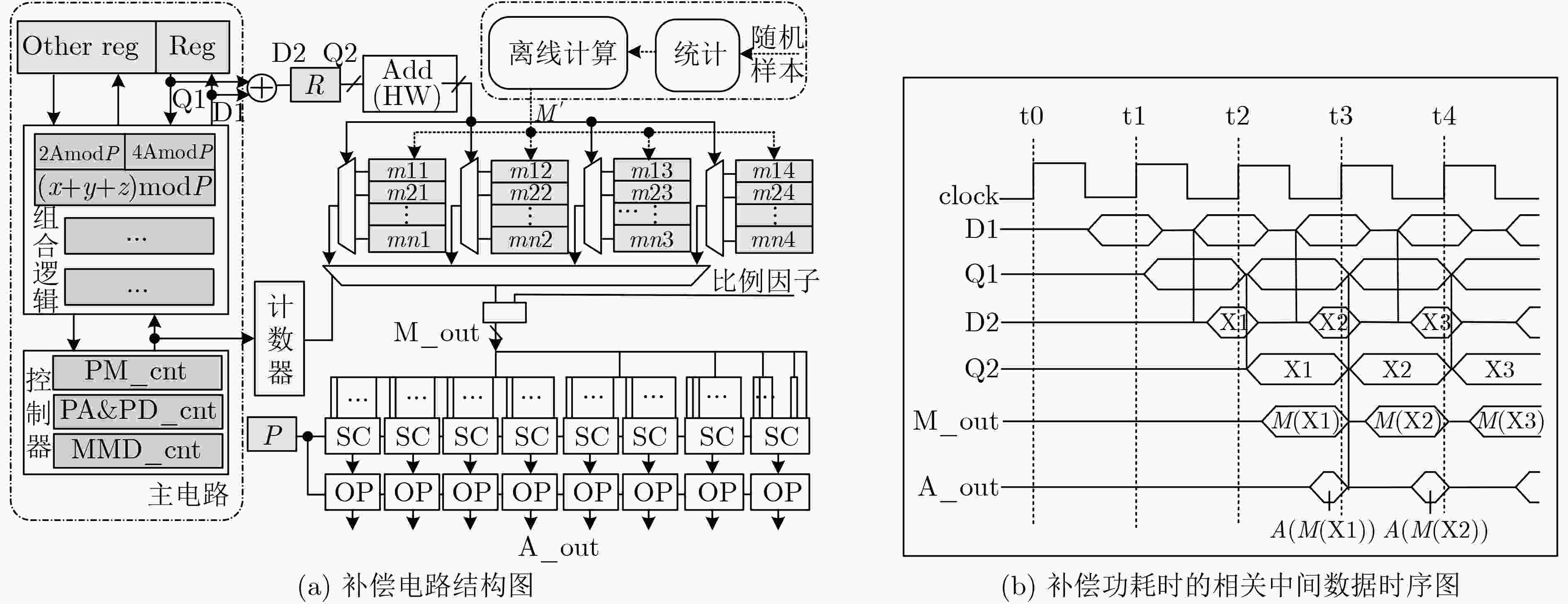
综合面积(mm2/kGates) 关键路径延时(ns) FPGA LUTs/FFs FPGA 功耗(W) 防护前 0.281/293.4 3.21 15851/3574 0.101 防护后 0.345/360.3 3.21 19687/4285 0.120 增加的百分比 +22.8% 0 +24.2%/+19.9% +18.8% 表 6 防护能力与电路代价对比分析
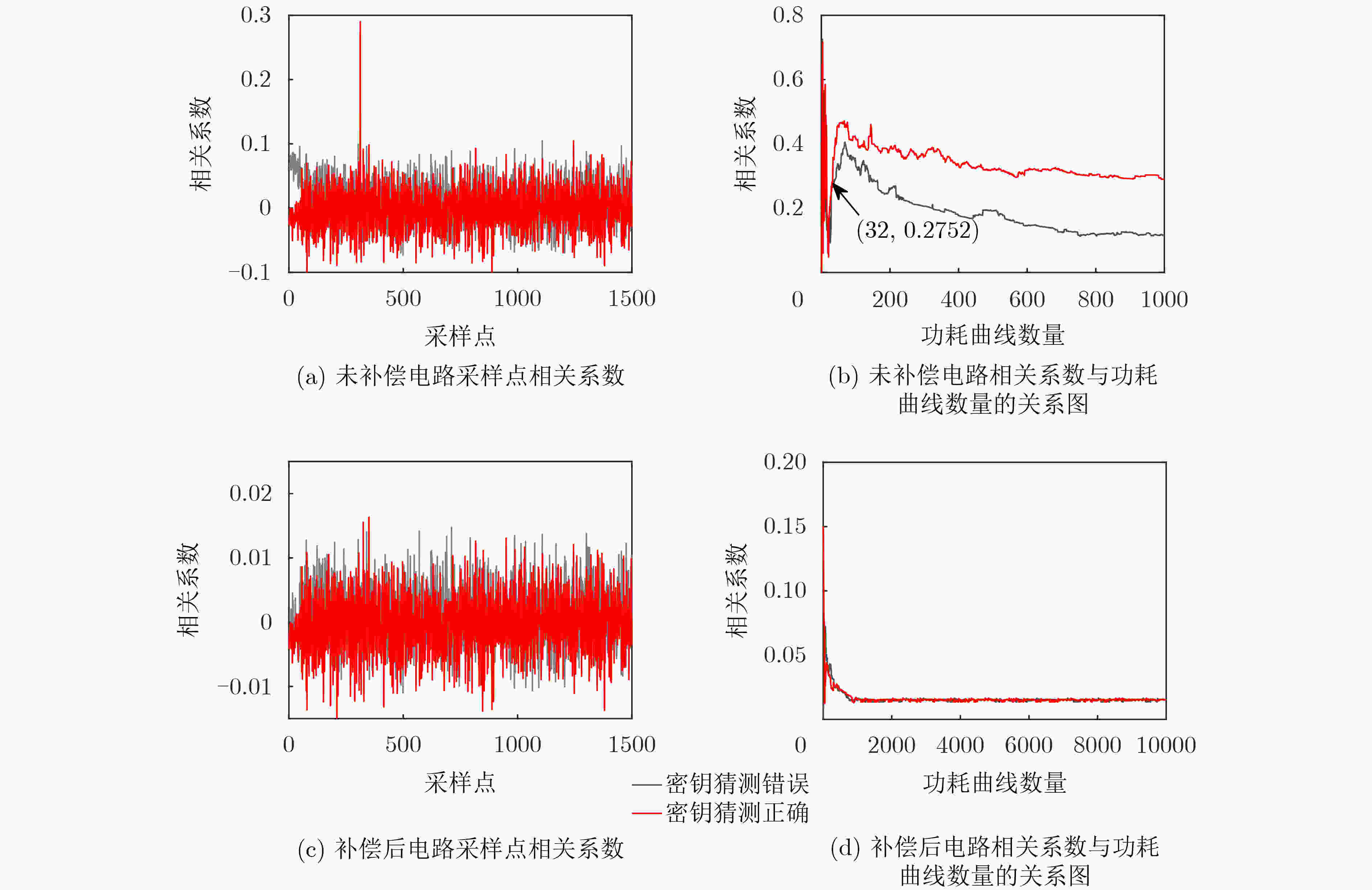
VLSI’14 [6] TIE’16[7] TDSC’18[16] TCAS-I’21[17] 本文 原理 基点随机化 中间点随机化 标量k随机化 射影坐标随机化 功耗补偿 域-位宽(bit) 素域-160 素域-163 素域-128 素域-256 素域-128 运算性能代价 +100.6% +53.8% +50% +62% +0 (点乘时间@频率/ms@MHz) (0.34@194) (0.6@316) (82.5@8) (0.089@222) (0.37@312) 面积代价(面积/kGates) +0(98) +0(189) +0(--) +0(194.7) +22.8%(360.3) 功耗代价(功率/mW) --(34.4) --(34.3) --(--) +50%(73.5) +18.8%(120.0) 最小泄露轨迹数MTD
防护能力提升倍数$ > {10^5}$
$ > 333$$ > 2 \times {10^4}$
$ > 250$$ > 5 \times {10^3}$
>119--
--$ > {10^4}$
$ > 312$ -
[1] 陈华, 习伟, 范丽敏, 等. 密码产品的侧信道分析与评估[J]. 电子与信息学报, 2020, 42(8): 1836–1845. doi: 10.11999/JEIT190853CHEN Hua, XI Wei, FAN Limin, et al. Side channel analysis and evaluation on cryptographic products[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1836–1845. doi: 10.11999/JEIT190853 [2] BELLIZIA D, BONGIOVANNI S, MONSURRÒ P, et al. Secure double rate registers as an RTL countermeasure against power analysis attacks[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2018, 26(7): 1368–1376. doi: 10.1109/TVLSI.2018.2816914 [3] KAR M, SINGH A, MATHEW S, et al. 8.1 Improved power-side-channel-attack resistance of an AES-128 core via a security-aware integrated buck voltage regulator[C]. 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, USA, 2017: 142–143. [4] SINGH A, KAR M, MATHEW S, et al. 25.3 A 128b AES engine with higher resistance to power and electromagnetic side-channel attacks enabled by a security-aware integrated all-digital low-dropout regulator[C]. 2019 IEEE International Solid- State Circuits Conference - (ISSCC), San Francisco, USA, 2019: 404–406. [5] CORON J S. Resistance against differential power analysis for elliptic curve cryptosystems[C]. The First International Workshop, CHES’99, Worcester, USA, 1999: 292–302. [6] LEE J W, CHUNG S C, CHANG H C, et al. Efficient power-analysis-resistant dual-field elliptic curve cryptographic processor using heterogeneous dual-processing-element architecture[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2014, 22(1): 49–61. doi: 10.1109/TVLSI.2013.2237930 [7] LIU Zilong, LIU Dongsheng, and ZOU Xuecheng. An efficient and flexible hardware implementation of the dual-field elliptic curve cryptographic processor[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2353–2362. doi: 10.1109/TIE.2016.2625241 [8] YEH L Y, CHEN P J, PAI Chenchun, et al. An energy-efficient dual-field elliptic curve cryptography processor for internet of things applications[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(9): 1614–1618. doi: 10.1109/TCSII.2020.3012448 [9] GOGNIAT G, WOLF T, BURLESON W, et al. Reconfigurable hardware for high-security/high-performance embedded systems: The SAFES perspective[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2008, 16(2): 144–155. doi: 10.1109/TVLSI.2007.912030 [10] YANG Jianwei, HAN Jun, DAI Fan, et al. A power analysis attack resistant multicore platform with effective randomization techniques[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2020, 28(6): 1423–1434. doi: 10.1109/TVLSI.2020.2971636 [11] 戴紫彬, 易肃汶, 李伟, 等. 椭圆曲线密码处理器的高效并行处理架构研究与设计[J]. 电子与信息学报, 2017, 39(10): 2487–2494.DAI Zibin, YI Suwen, LI Wei, et al. Research and design of efficient parallel processing architecture for elliptic curve cryptographic processor[J]. Journal of Electronics &Information Technology, 2017, 39(10): 2487–2494. [12] MANGARD S, OSWALD E, POPP T, 冯登国, 周永彬, 刘继业, 等译. 能量分析攻击[M]. 北京: 科学出版社, 2010: 56–63.MANGARD S, OSWALD E, POPP T, FENG Dengguo, ZHOU Yongbin, LIU Jiye, et al. translation. Power Analysis Attacks: Revealing the Secrets of Smart Cards[M]. Beijing: Science Press, 2010: 56–63. [13] SHAN Weiwei, ZHANG Shuai, XU Jiaming, et al. Machine learning assisted side-channel-attack countermeasure and its application on a 28-nm AES circuit[J]. IEEE Journal of Solid-State Circuits, 2020, 55(3): 794–804. doi: 10.1109/JSSC.2019.2953855 [14] SHAN Weiwei, ZHANG Shuai, and HE Yukun. Machine learning based side-channel-attack countermeasure with hamming-distance redistribution and its application on advanced encryption standard[J]. Electronics Letters, 2017, 53(14): 926–928. doi: 10.1049/el.2017.1460 [15] 刘振宏, 马绍汉. 离散最优化算法[M]. 北京: 科学出版社, 2012: 36–38.LIU Zhenhong and MA Shaohan. Discrete Optimization Algorithms[M]. Beijing: Science Press, 2012: 36–38. [16] LIU Zhe, LONGA P, PEREIRA G C C F, et al. on embedded devices with strong countermeasures against side-channel attacks[J]. IEEE Transactions on Dependable and Secure Computing, 2020, 17(3): 536–549. [17] CHOI P, LEE M K, and KIM D K. ECC coprocessor over a NIST prime field using fast partial Montgomery reduction[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(3): 1206–1216. doi: 10.1109/TCSI.2020.3039753 -





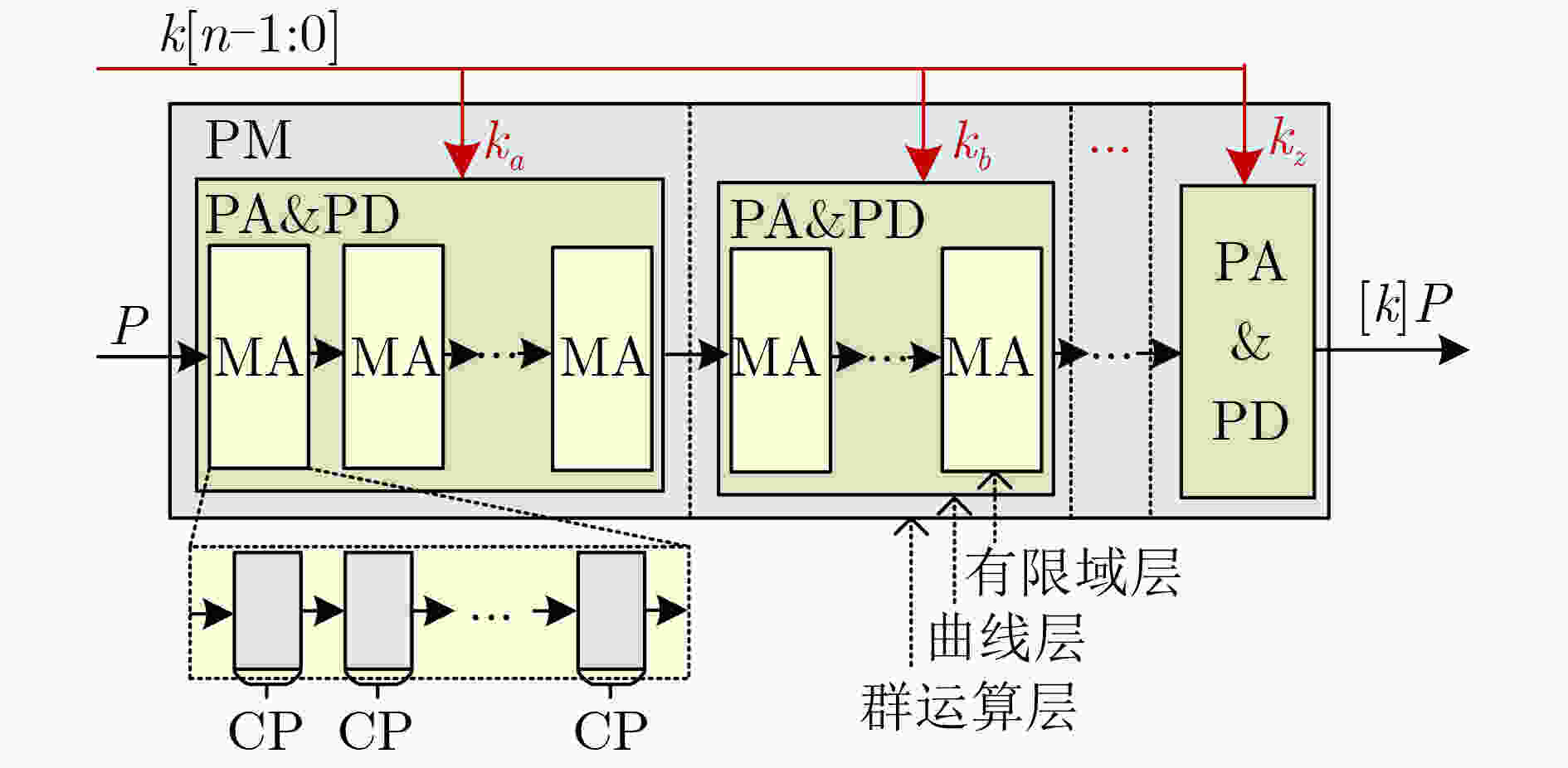
 下载:
下载:
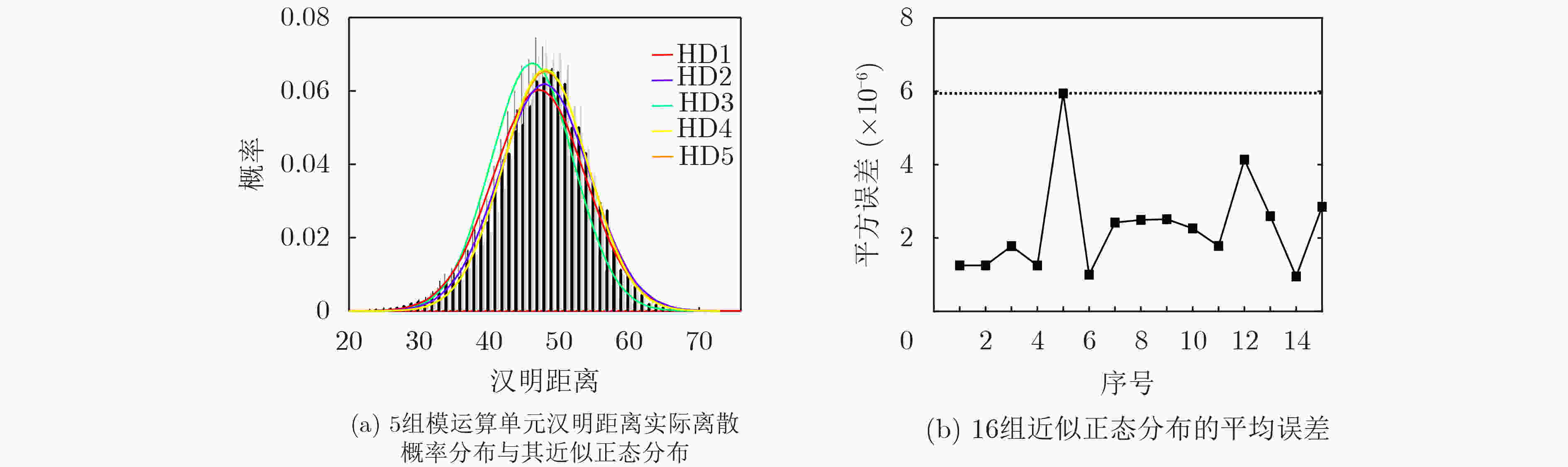
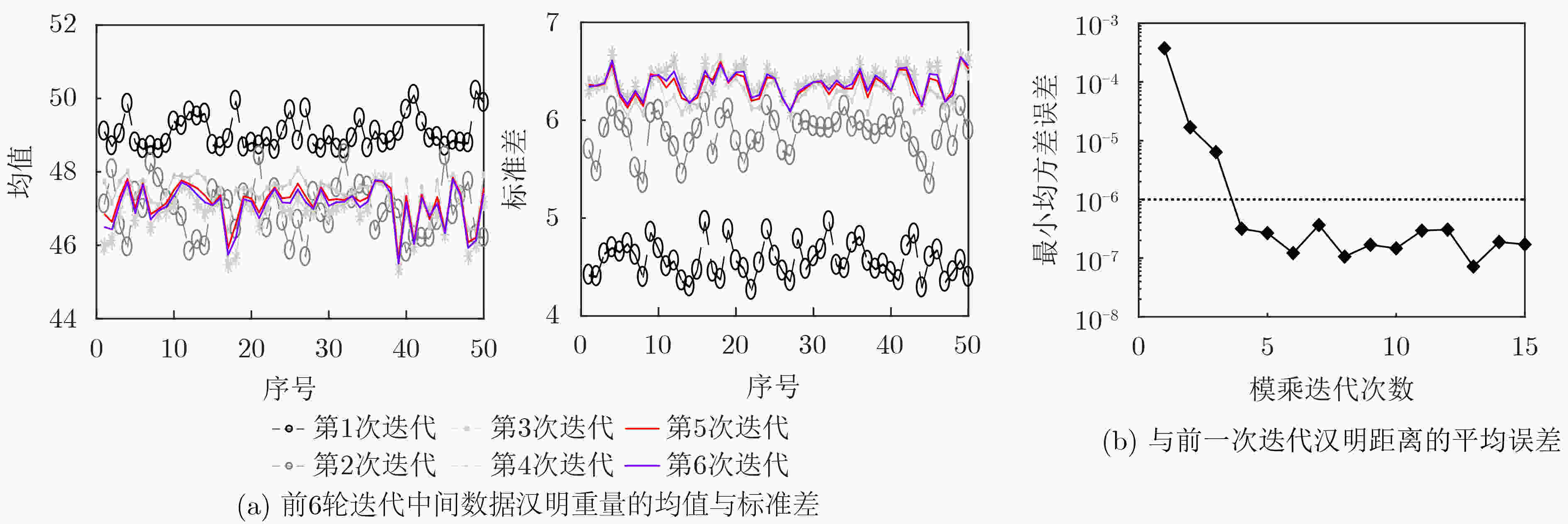
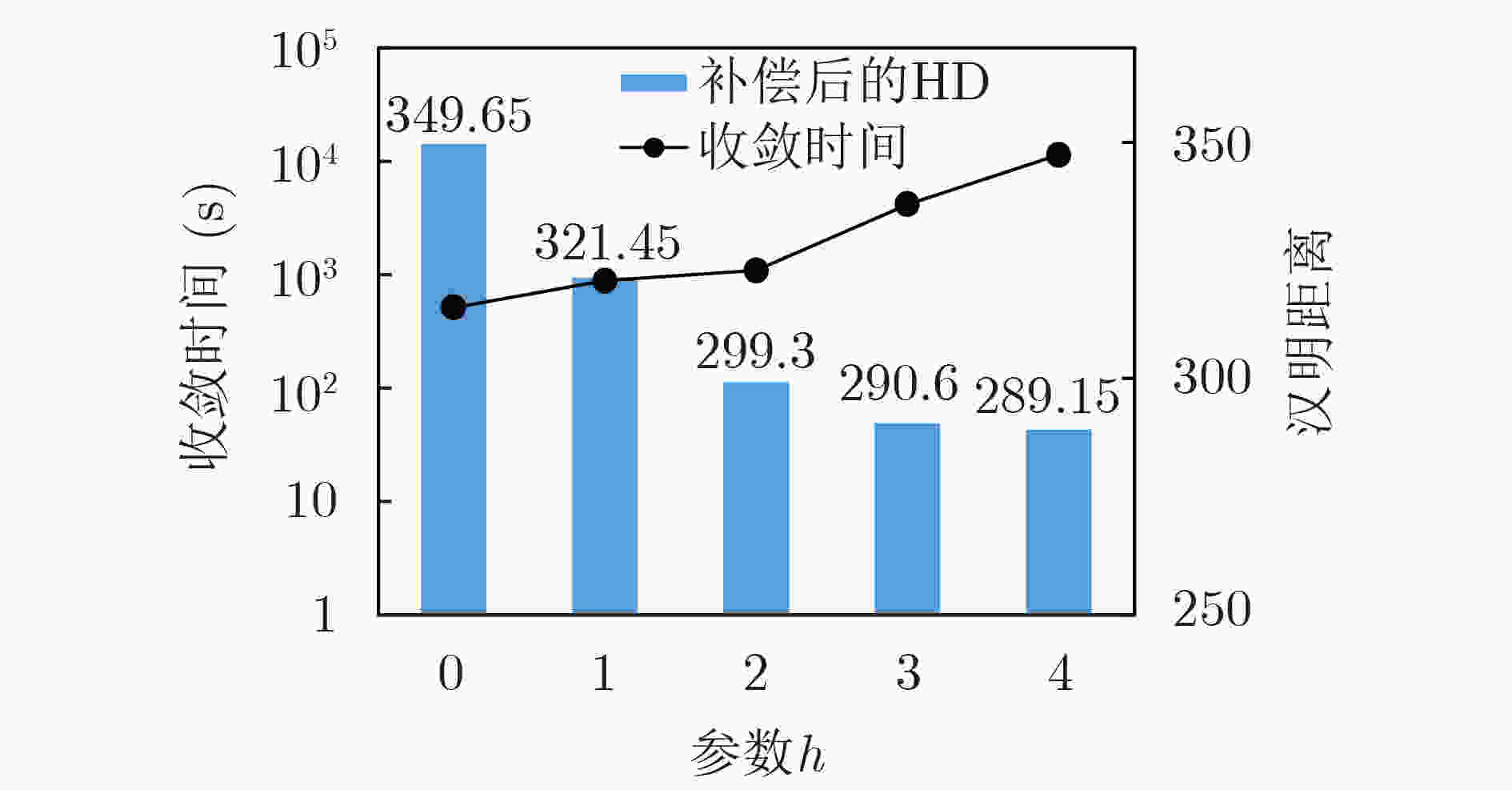





 下载:
下载:
