| [1] |
WANG Qi, ZHANG Rong, YANG Lieliang, et al. Non-orthogonal multiple access: A unified perspective[J]. IEEE Wireless Communications, 2018, 25(2): 10–16. doi: 10.1109/MWC.2018.1700070
|
| [2] |
DAI Linglong, WANG Bichao, DING Zhiguo, et al. A survey of non-orthogonal multiple access for 5G[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2294–2323. doi: 10.1109/COMST.2018.2835558
|
| [3] |
SAITO Y, BENJEBBOUR A, KISHIYAMA Y, et al. System-level performance evaluation of downlink non-orthogonal multiple access (NOMA)[C]. The IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 2013: 611–615.
|
| [4] |
DING Zhiguo, LEI Xianfu, KARAGIANNIDIS G, et al. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(10): 2181–2195. doi: 10.1109/JSAC.2017.2725519
|
| [5] |
王夕予, 许晓明, 陈亚军. 非理想连续干扰消除下非正交多址接入上行传输系统性能分析[J]. 电子与信息学报, 2019, 41(12): 2795–2801. doi: 10.11999/JEIT181165WANG Xiyu, XU Xiaoming, and CHEN Yajun. Performances analysis in uplink non-orthogonal multiple access system with imperfect successive interference cancellation[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2795–2801. doi: 10.11999/JEIT181165
|
| [6] |
ZHU Jianyue, WANG Jiaheng, HUANG Yongming, et al. On optimal power allocation for downlink non-orthogonal multiple access systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2744–2757. doi: 10.1109/JSAC.2017.2725618
|
| [7] |
YANG Zheng, DING Zhiguo, FAN Pingzhi, et al. On the performance of non-orthogonal multiple access systems with partial channel information[J]. IEEE Transactions on Communications, 2016, 64(2): 654–667. doi: 10.1109/TCOMM.2015.2511078
|
| [8] |
于宝泉, 蔡跃明, 胡健伟. 认知无线电非正交多址接入随机网络物理层安全性能分析[J]. 电子与信息学报, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049YU Baoquan, CAI Yueming, and HU Jianwei. Performance analysis of physical layer security for cognitive radio non-orthogonal multiple access random network[J]. Journal of Electronics &Information Technology, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049
|
| [9] |
GANJI M and JAFARKHANI H. Interference mitigation using asynchronous transmission and sampling diversity[C]. Proceedings of 2016 IEEE Global Communications Conference (GLOBECOM), Washington, USA, 2016: 1–6.
|
| [10] |
CUI Jianxiong, DONG Guangliang, ZHANG Shengli, et al. Asynchronous NOMA for downlink transmissions[J]. IEEE Communications Letters, 2017, 21(2): 402–405. doi: 10.1109/LCOMM.2016.2619339
|
| [11] |
ZOU Xun, HE Biao, and JAFARKHANI H. An analysis of two-user uplink asynchronous non-orthogonal multiple access systems[J]. IEEE Transactions on Wireless Communications, 2019, 18(2): 1404–1418. doi: 10.1109/TWC.2019.2892486
|
| [12] |
DANG Xiaoyu, LIU Zhaotong, LI Baolong, et al. Noncoherent multiple-symbol detector of binary CPFSK in physical-layer network coding[J]. IEEE Communications Letters, 2016, 20(1): 81–84. doi: 10.1109/LCOMM.2015.2499249
|
| [13] |
EMMANUELE A, ZANIER F, BOCCOLINI G, et al. Spread-spectrum continuous-phase-modulated signals for satellite navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3234–3249. doi: 10.1109/TAES.2012.6324699
|
| [14] |
RICE M and GAGAKUMA E. Approximate MLSE equalization of SOQPSK-TG in aeronautical telemetry[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(2): 769–784. doi: 10.1109/TAES.2018.2864807
|
| [15] |
李赛, 党小宇, 郝崇正, 等. 改进的航空遥测信道探测[J]. 航空学报, 2022, 43(1): 324881. doi: 10.7527/S1000-6893.2020.24881LI Sai, DANG Xiaoyu, HAO Chongzheng, et al. Improved aeronautical telemetry channel sounding[J]. Acta Aeronauticaet Astronautica Sinica, 2022, 43(1): 324881. doi: 10.7527/S1000-6893.2020.24881
|
| [16] |
PROAKIS J G, SALEHI M, 张力军, 张宗橙, 宋荣方, 等译. 数字通信[M]. 5版. 北京: 电子工业出版社, 2011: 81–91.PROAKIS J G, SALEHI M, ZHANG Lijun, ZHANG Zongcheng, SONG Rongfang, et al. translation. Digital Communications[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2011: 81–91.
|
| [17] |
XIAN Liang, PUNNOOSE R, and LIU Huaping. Simplified receiver design for STBC binary continuous phase modulation[J]. IEEE Transactions on Wireless Communications, 2008, 7(2): 452–457. doi: 10.1109/TWC.2008.060628
|
| [18] |
ZOU Xun, GANJI M, and JAFARKHANI H. Downlink asynchronous non-orthogonal multiple access systems with imperfect channel information[C]. 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, USA, 2019: 1–6.
|
| [19] |
FANG Fang, ZHANG Haijun, CHENG Julian, et al. Joint user scheduling and power allocation optimization for energy-efficient NOMA systems with imperfect CSI[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2874–2885. doi: 10.1109/JSAC.2017.2777672
|
| [20] |
ETSI. ETSI TS 136 213 V10.1. 0 LET; evolved universal terrestrial radio access (E-UTRA); Physical layer procedures[S]. ETSI, 2011.
|
| [21] |
CLERCKX B and OESTGES C. MIMO Wireless Networks[M]. 2nd ed. Amsterdam: Elsevier, 2013: 106–122.
|
| [22] |
LIU Chang and BEAULIEU N C. Exact BER performance for symbol-asynchronous two-user non-orthogonal multiple access[J]. IEEE Communications Letters, 2021, 25(3): 764–768. doi: 10.1109/LCOMM.2020.3038951
|





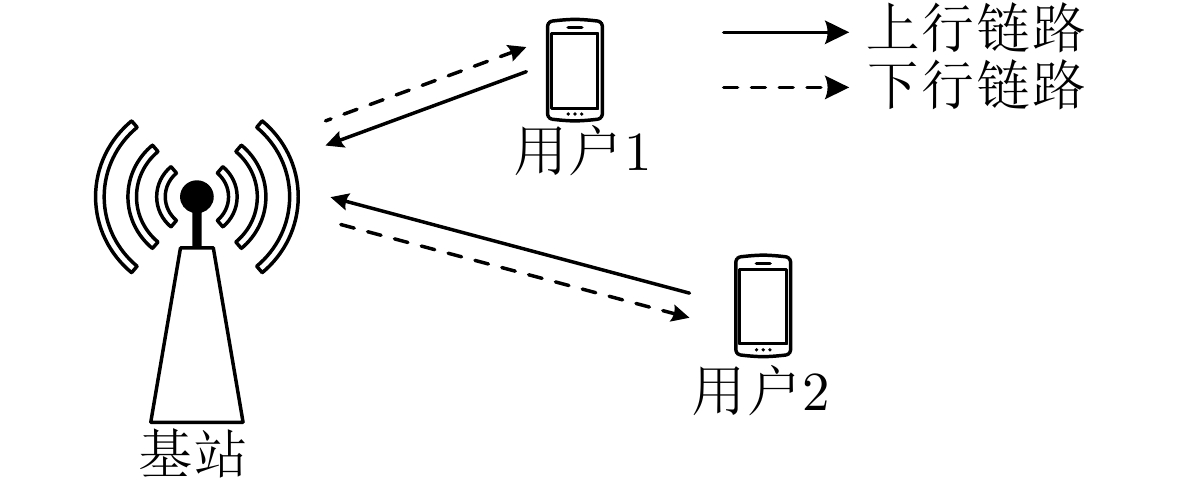
 下载:
下载:
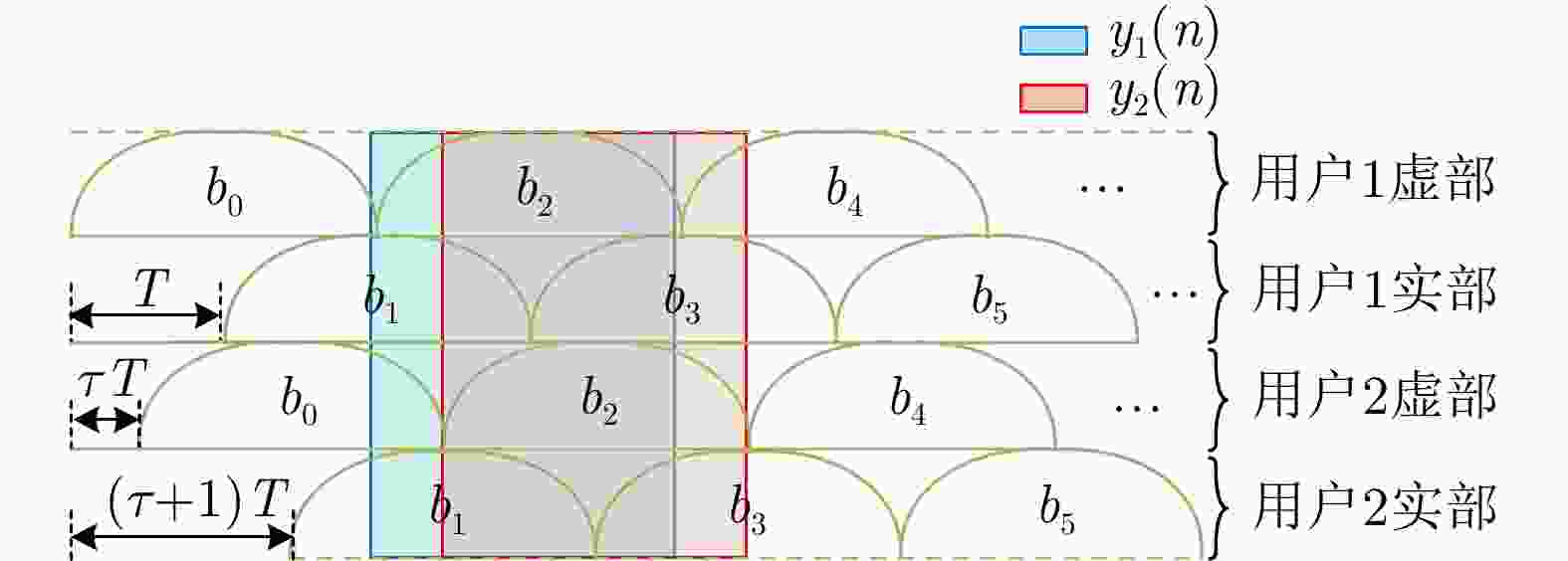
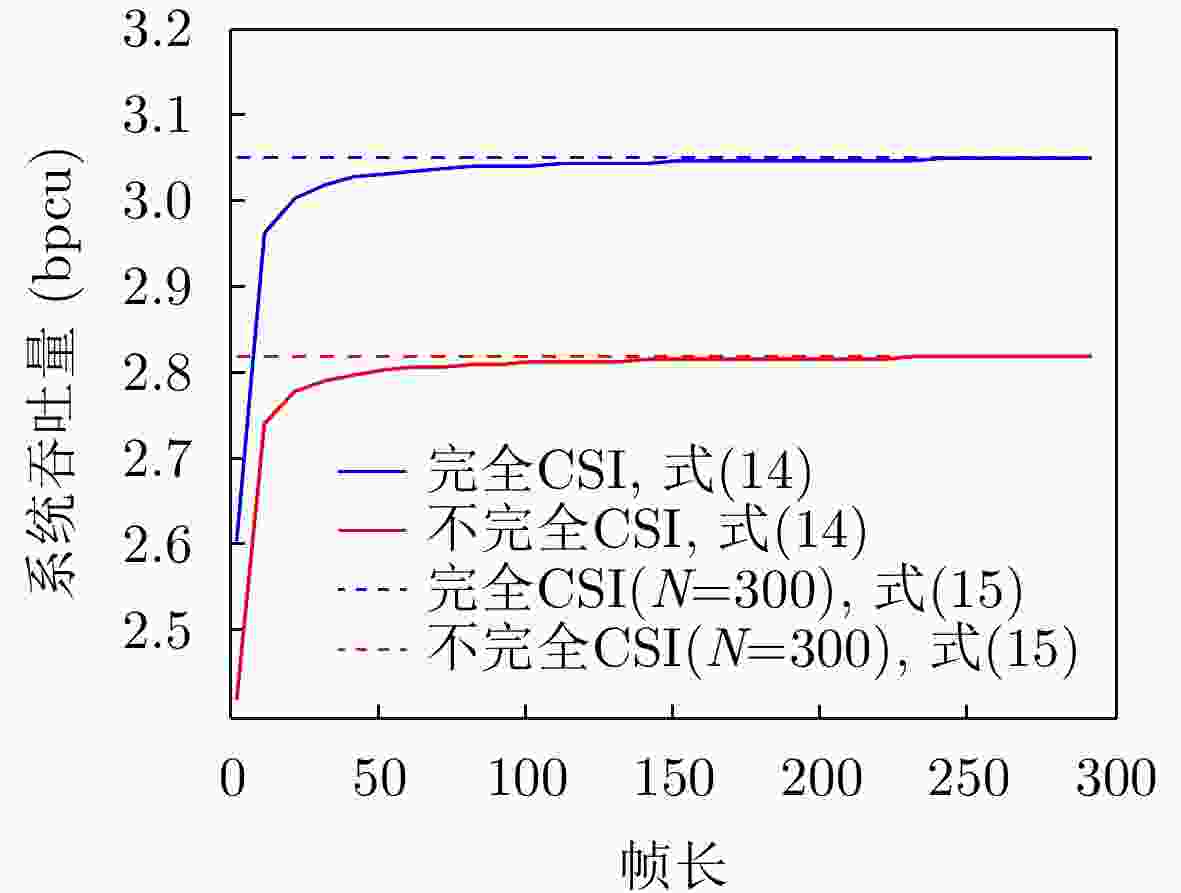
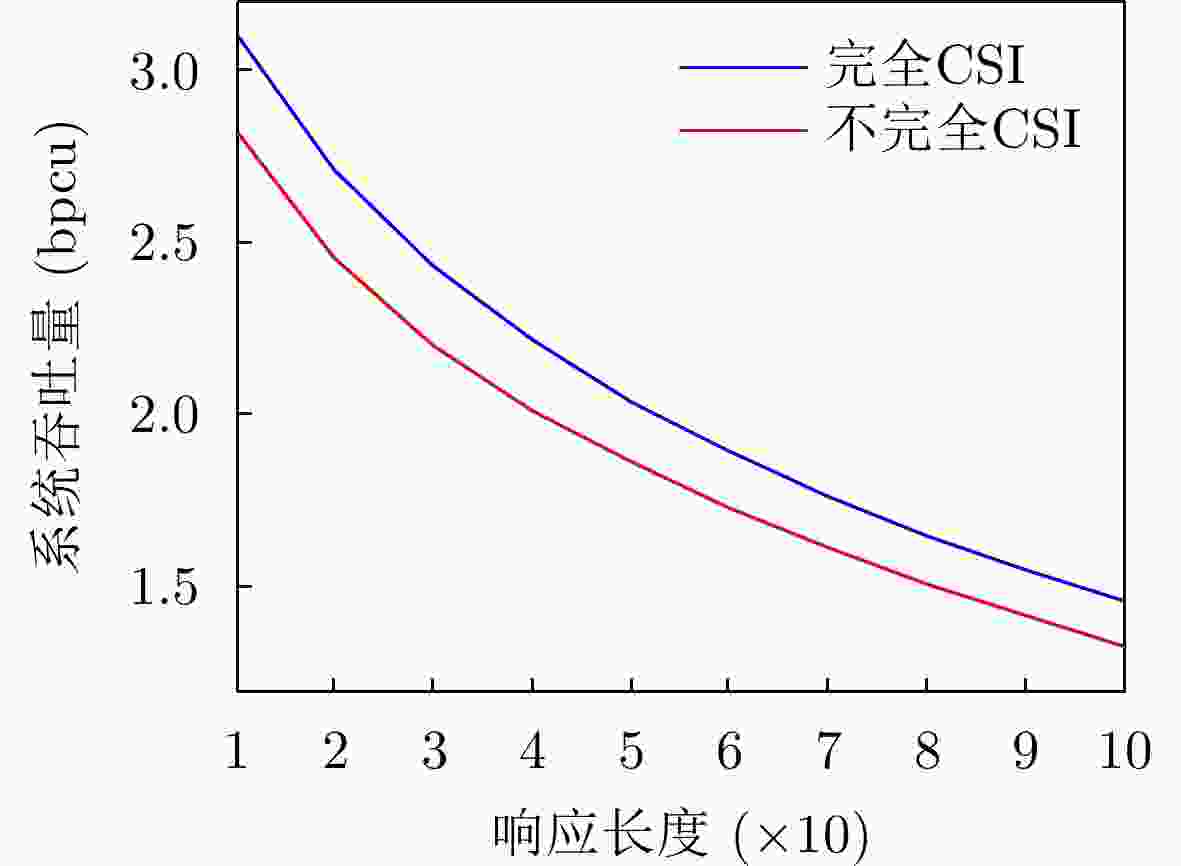


 下载:
下载:
